近场动力学法频散特性及其在岩石层裂分析中应用

卢志堂， 王志亮, 2

(1.同济大学 土木工程学院，200092 上海； 2.合肥工业大学 土木与水利工程学院，230009 合肥)



近场动力学法频散特性及其在岩石层裂分析中应用

卢志堂1， 王志亮1, 2

(1.同济大学 土木工程学院，200092 上海； 2.合肥工业大学 土木与水利工程学院，230009 合肥)

摘要:为了解近场动力学方法(peridynamics, PD)的计算精度，考察该法用于岩石层裂破坏模拟的效果，对PD进行了频散分析和算法验证.首先由频散分析后发现：当空间步长不变时，随影响域变大PD法频散愈严重；而空间步长减小时，影响域节点数不变，其频散会变弱；当影响域大小不变时，内部划分节点越密集，频散越弱.其次，通过该方法与传统有限差分法的比较表明PD离散方程可看作一系列差分方程的组合，其截断误差为影响域半径δ的二阶无穷小；当δ为Δx时，PD算法与中心差分法是等价的，且此时计算精度最高.最后，通过PD法应用于岩杆一维层裂模拟分析，探讨了其空间步长、影响域尺寸对计算结果的影响，得出层裂时间、层裂位置及损伤分布情况，并与层裂试验进行对比分析.PD可用于岩石层裂破坏分析，将FDM和PD法两者结合进行层裂模拟时，计算时间少、优势明显.

关键词:近场动力学；频散特性；有限差分法；岩杆；层裂

材料断裂损伤是工程领域热点问题之一，除了借助相关实验手段外，研究人员也在积极寻求数值方法上的突破，以期弄清楚材料裂纹产生及其破坏机理，并进而能对断裂进行预警.虽然有限元和有限差分等方法在工程分析中得到了广泛应用，但这些传统数值方法大多都是基于经典连续介质力学的偏微分方程而来，在解决不连续问题时会产生奇异值，很难实现对材料内部裂缝产生与损伤发展的模拟.为很好地刻画裂缝生成和材料损伤演化，革新数值方法和发展相关理论的研究一直未间断，而近场动力学(peridynamics，PD)正是其中的理论之一[1].文献[2]对经典连续介质力学进行了重建，提出了PD 理论，将传统的偏微分方程替换为积分方程，并可直接对不连续介质力学问题(比如裂缝扩展与分叉)进行分析.在一定条件下，选择合适的响应函数，PD方程收敛于经典连续介质力学方程[3].将PD方程离散，结合损伤模型就可实现对脆性和延性材料的断裂问题进行模拟.该方法理论清晰、过程简单，已有模拟结果与试验数据吻合较好[4-8].在国内，文献[9-10]利用PD理论模拟了混凝土的脆性损伤情况，指出PD法可很好刻画和模拟混凝土在拉伸情况下的损伤累积与渐进破坏过程.

虽然PD方法能很好反映材料断裂形式，但是材料断裂前，通常需要经历一段连续变形过程，此时该方法的频散特性还有待深入研究；另一方面，PD的计算效果与基于连续介质力学发展起来的数值算法(如FDM，有限差分法)相比，是否具有优势？能否将其与现有方法联合应用于材料断裂分析也值得探讨.

1PD法计算原理

1.1基本方程

如图1所示，材料占据空间域B，x为B内一材料点，Hx为x的影响域，δ为Hx的半径.假设x与其影响域Hx内的另一材料点x′通过连接键产生相互作用，作用力f为

(1)

式中|x′-x|≤δ，x和x′分别为材料点x的位置矢量，u表示位移矢量.

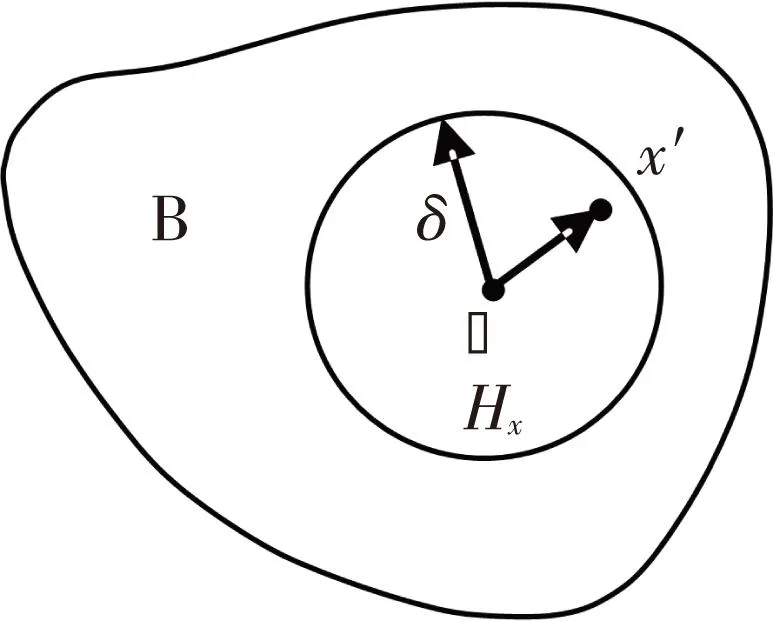
图1　空间域B与影响域Hx示意

材料点x的PD方程为

(2)

式中:ρ为密度，ü为x点加速度，Vx′为x′点所占体积，b为体力.ξ=x′-x，为相对位置矢量，η=u(x,t)-u(x,t)，为相对位移，见图2.

相互作用力f可写为

(3)

图2　影响域内相对位置与相对位移

1.2本构关系与损伤准则

f(η,ξ)可写成连接键伸长率的函数，即PD本构关系式：

(4)

式中:cm表示微弹模，在一维、二维和三维条件下依次为2E/(Aδ2)、9E/(πδ3)、12E/(πδ4)[11]，E表示弹性模量，A表示材料点占据的面积，s表示材料点间连接键伸长率，其表达式为

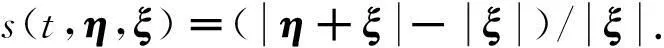
(5)

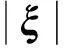
(6)

式中s0为连接键临界伸长率，当s ≥ s0时，连接键断裂，且不可恢复.

x点的局部损伤φ可表示为失效的连接作用与全部连接的比值，即

(7)

根据局部损伤可判断材料内部裂缝的发育及传播过程.通常情况下，需定义损伤值φ0作为判断裂缝是否产生的准则，本文借鉴文献[4]建议值，即φ0= 0.3.

1.3求解思路

式(2)通常借助数值积分处理，写成求和表达式：

(8)

式中：i和p分别表示计算节点与其影响域内的节点编号，Vp表示点p的在影响域内占据的体积.

图3给出二维节点分布，图中节点间距均为Δx，每个节点占据的面积为(Δx)2.Vp近似[12]为

其中V = (Δx)3.

采用时域中心差分计算加速度：

(10)

式中:上标n表示时步数，Δt为时间间隔，计算的稳定性条件为Δt ≤Δx/c，c表示波速.

PD法数值计算流程见图4.

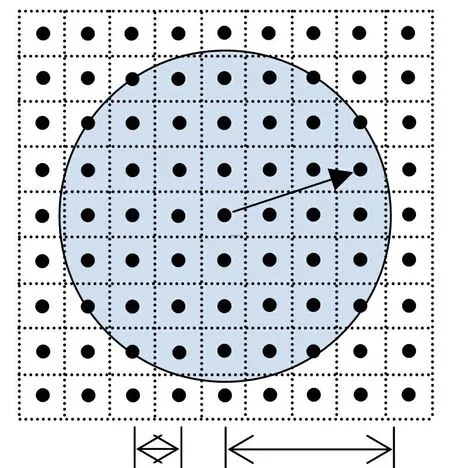
图3　PD计算的离散域示意

图4　PD程序流程图

2频散特性分析

虽然目前已有研究表明PD在模拟脆性材料破坏过程与试验吻合较好，但对其在材料破坏前的模拟效果关注较少.文献[13]发现利用PD数值计算时存在频散现象，所谓数值频散实质上是一种因离散化求解波动方程而产生的伪波动[14]，这种频散不同于波动方程本身引起的物理频散，而是PD离散方程所固有的本质特征.这会导致波在传播过程中，波前形状发生变化，并且逐渐散开，进而引起模拟得出的波速和裂缝扩展速度失真.数值频散对研究材料中波传播过程，尤其是在冲击荷载(高频波成分较多，数值频散愈严重)作用下是不利的.本节将结合频域分析，对PD法的数值频散特性进行分析，以求压制数值频散，提高计算精度.以一维方程为例，将式(2)的解写成一般形式：

(11)

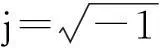
(12)

考虑影响域半径、空间步长的变化，得出频散曲线(见图5，纵坐标表示频率ω(2π)-1，横坐标表示波数)，其中参数按照黑云母花岗岩参数给出：弹性模量E= 20 GPa，ρ= 2 620 kg·m-3.

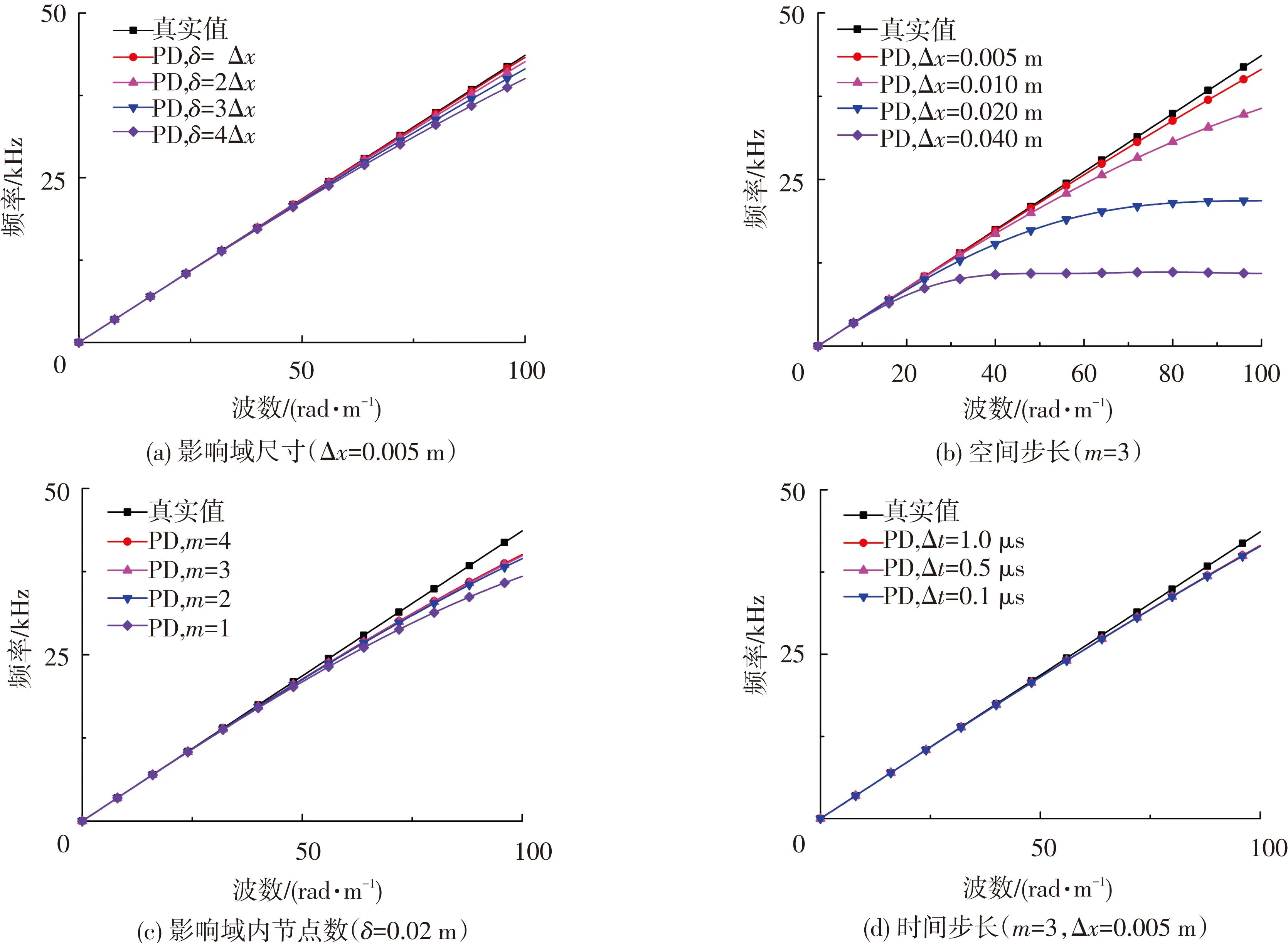
图5　频散特性影响因素

图5(a)中空间步长Δx= 0.005 m保持不变，不断增大影响域，不难发现δ= Δx时频散曲线与真实曲线最接近；m越大，得到的曲线与真实曲线相差越大，即影响域增大时，PD方法数值频散越严重；同时还能看出，频率越大，PD方法频散愈加强烈.这表明在利用PD法计算高频荷载作用时，确定空间步长后，应尽量选取较小的影响域，否则会降低其计算精度；图5(b)给出m= 3时，空间步长Δx对PD方法频散性质的影响，当Δx从0.005 m增大到0.02 m时，频散急剧加重；根据图5(c)，当保持影响域半径δ= 0.02 m，m从1增大到4时对应的频散曲线愈接近真实曲线，这表明影响域内节点越密集，PD方法精度越高；图5(d)给出了Δt从1 μs减小到0.1 μs对PD方法频散性质的影响，发现频散曲线对时间步长不太敏感(Δt取值已满足PD法的稳定性条件).通常在模拟裂缝开展时，取影响域半径为δ= (3~4)Δx[4, 6]，但增大影响域会降低PD方法模拟波传播问题的精度，这就要求计算时空间步长应尽量取小，或者尝试将预估裂缝区处节点局部进行加密.

3PD算法验证及应用

3.1传统算法对比

有限差分法(FDM)是一种应用广泛的数值方法，在岩土力学问题上具有很好的适用性[15-18].下文将PD方法与FDM进行具体比较，分析两者之间的差别和联系.

不考虑体力和损伤，可将式(8)详细展开，以尝试深入分析PD和FDM的差别.一维条件下，影响域δ= Δx时，节点i的影响域内只有两个节点(i- 1，i+ 1)，于是式(8)变为

(13)

当δ=2Δx，3Δx…mΔx时，依次可得：

(14)

(15)

(16)

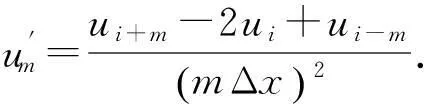
而一维波动方程经过FDM离散后变为

(17)

对比发现，式(17)即式(13)，这说明当δ= Δx时，PD法和FDM等价.需要强调的是，式(13)给出的是一种临界情况，即节点i-1和i+1恰好在节点i影响域边界上，在PD计算过程中，影响域内的节点位置不断更新，当材料受拉伸时，节点i-1或i+1可能离开影响域，因此在计算时，δ取值要比节点间距整数倍略大来保证计算过程中影响域内节点数不变，这样导致FDM和δ=Δx的PD计算结果会略有差别，下面的算例分析会体现这一点.

根据泰勒级数展开可知，式(13)和(14)的截断误差分别为O[(Δx)2]和O[(2Δx)2]，这也表明随着影响域增大，PD方法的误差增大.一般，当影响域半径δ=mΔx时，得到的PD离散方程可看出一系列差分方程的组合，其截断误差变为O(δ2)，这样从理论上说明了影响域变大，该方法频散严重(计算精度降低)的原因.

通过将PD与FDM对比分析，发现PD离散方程可写为差分方程组合形式，仅在影响域δ=Δx情况下，PD与FDM计算效果相同，影响域增大之后，其计算精度降低，表明差分法在计算连续变形方面具有优势.利用PD计算断裂问题时，通常需要取较大影响域(δ= (3~4)Δx)才能很好模拟材料破坏过程[4, 6]，这反而会降低PD法对波传播过程的计算精度.为尽可能保证计算精度，在材料破坏之前采用δ=Δx的PD法或直接用FDM，而当材料临近破坏时(文中按连接键伸长率达到临界值考虑)，再采用影响域较大的PD法进行计算，将使得计算结果更精确.

3.2岩石层裂过程的PD分析

这里以岩石一维层裂试验为研究对象.根据一维波动理论，对杆状试样入射端施加应力脉冲，应力波在杆自由端反射形成拉伸波，当强度达到岩石的抗拉强度时会引起拉伸断裂[20].然后根据层裂位置，就可间接求出层裂强度，并可讨论应变率效应[21-27].根据PD法频散性质，选择合适的网格参数压制数值频散，可有效避免计算求得的应力波形在向岩杆自由端传播过程保持足够稳定，保证计算结果具有较高精度.

计算中首先施加强度较小的压力脉冲，采用PD法分析岩杆中波传播特点，对应的定解问题可写成

(18)

式中p(t)表示杆件所受的冲击荷载，试验中荷载时程曲线见图6，这里将其简化为上升沿较短的三角波进行分析.三角波峰值pm为8.9 MPa，出现时刻tp=0.04 ms，持续时间t0=0.12 ms.

首先采用PD法求解该问题，岩杆长l=1 m，取Δx=0.005 m，Δt=1 μs.考虑了4个不同的影响域：δ分别为Δx、2Δx、4Δx和8Δx，同时将FDM(Δx=0.005 m)计算的杆中点(x=0.5 m)应力时程曲线给出(见图7(a)，纵坐标表示轴向应力，横坐标为时间)，规定拉为正.可看出FDM和δ=Δx的PD方法计算结果比较接近，但仍存在一定偏差(上文在与FDM对比时已指出)；δ为Δx和2Δx时，图7(a)得出两曲线基本吻合；当δ增大到4Δx时，t= 0.5 ms后应力波波形发生频散，计算结果吻合度变差；当δ为8Δx时，从t=0.8 ms后应力波因数值频散而失真，说明随着影响域增大，PD法计算结果变差.图7(b)中令δ=3Δx，首先保持t0不变，Δx由0.005 m增为0.01 m，约在0.5 ms后出现频散(带●标记的曲线)，而带■标记的曲线无明显频散，反映了影响域增大，PD法频散加重；当Δx不变，t0由0.12 ms增大至0.24 ms时(即频率降低)，波形保持较好，说明随t0增大，频散效应变弱.通过该对该算例的分析，也可看出PD方法的计算效果与上文频散分析结论一致.

采用PD计算断裂问题时，若Δx，δ等参数选择不当，产生的数值频散会使应力波在传播过程中分散开来，致使尾端加载的压应力波波形偏离原始波形，产生错误的计算结果.

图6　荷载时程曲线

为说明PD法对层裂模拟分析的效果，方便起见，直接假设试样的抗拉强度σt为10 MPa，增大压力脉冲p(t)，使试样发生层裂.计算时考虑m、Δx、pm和t0等参数的变化，试件断裂(φ0= 0.3)时尾端损伤分布见图8(a)所示(纵坐标为损伤，横坐标表示杆件尾部位置).其中参数m、Δx、pm、t0、断裂位置xF，断裂发生时间tF列于表1.根据曲线1~3，可看出当影响域半径由3Δx增大到10Δx时，断裂的区域和发生时间增大，但彼此相差不大.当空间步长减小到0.000 5 m时，对比曲线4和5，影响域增大时，断裂区域和发生时间也有变大.同时还发现，空间步长分别为0.001 和0.000 5 m时，断裂的区域和发生时间相差不大.为了考察冲击荷载作用时间对层裂位置影响，特将t0增大到0.24 ms并得出断裂时损伤分布，见图8(a)中曲线6.对比曲线1和6可看出，层裂位置距自由端变远，这符合拉应力波峰值到时延迟，致使层裂位置远离自由端.曲线7对应的冲击荷载峰值强度pm为15 MPa，与曲线1相比，层裂位置更加靠近自由端，这是由于冲击荷载强度提高，反射后拉应力峰值达到岩石层裂强度所需时间缩短.图8(b)给出图8(a)中曲线1对应试件尾部拉应力区随时间发展情况，可以发现随时间增大，拉应力逐渐增大，当t=0.439 5 ms时，尾部拉应力峰值达到层裂强度，此时岩杆拉伸断裂瞬间发生.以上分析表明PD法用于岩石一维层裂模拟可行，效果令人满意.

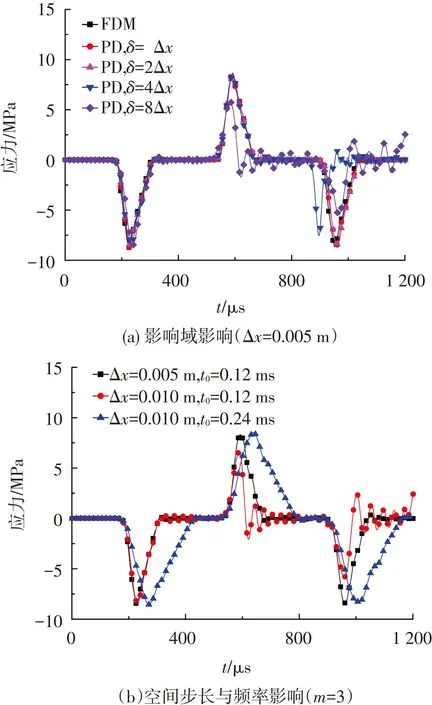
图7　岩杆中点的应力时程曲线

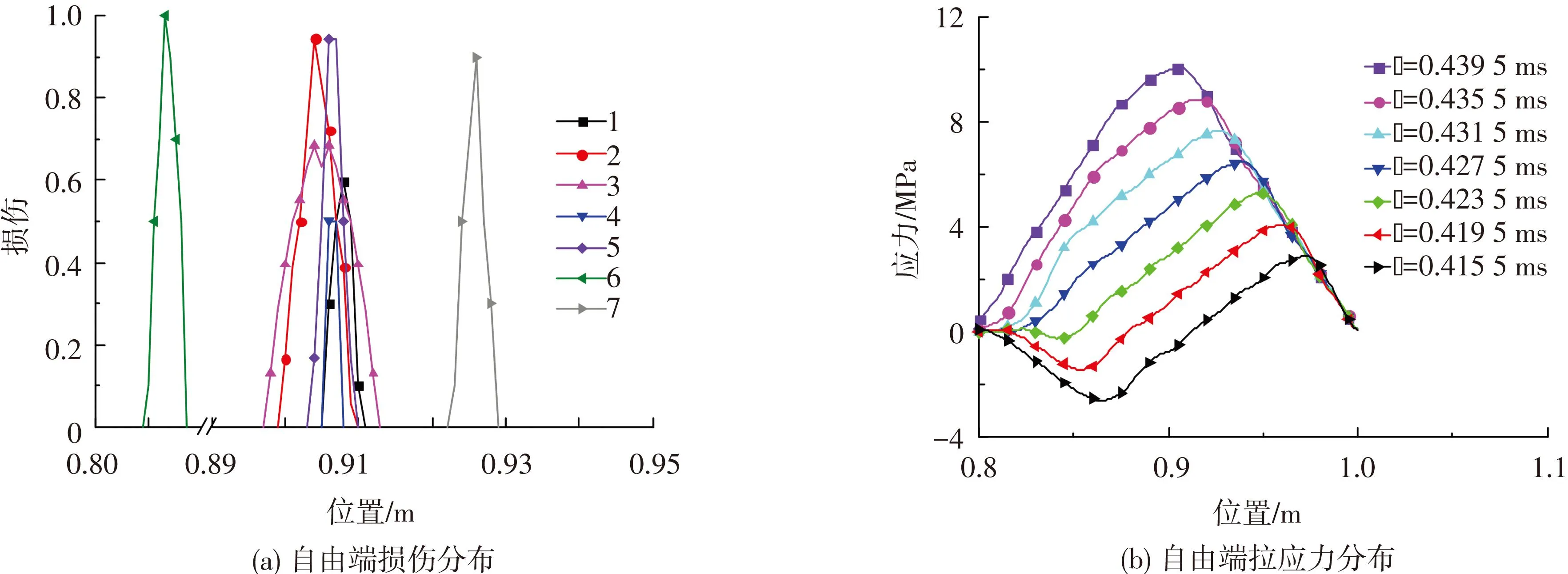
图8　层裂现象PD法模拟

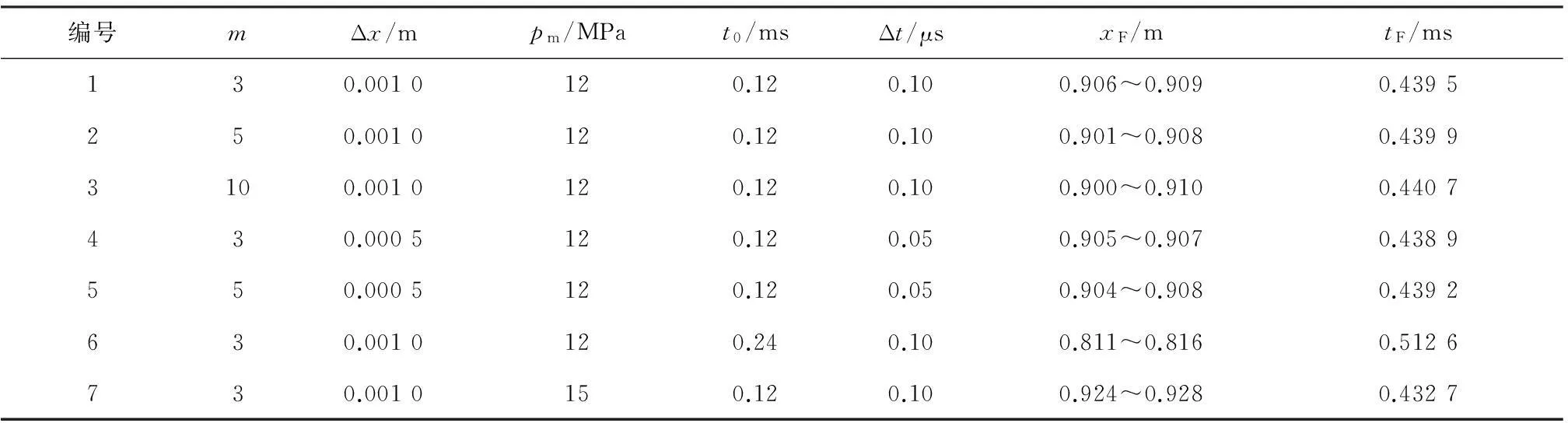
编号mΔx/mpm/MPat0/msΔt/μsxF/mtF/ms130.0010120.120.100.906~0.9090.4395250.0010120.120.100.901~0.9080.43993100.0010120.120.100.900~0.9100.4407430.0005120.120.050.905~0.9070.4389550.0005120.120.050.904~0.9080.4392630.0010120.240.100.811~0.8160.5126730.0010150.120.100.924~0.9280.4327

3.3试验验证

试验中采用的岩杆见图9(a)，杆长0.99 m，直径0.07 m，密度2 620 kg·m-3.由于岩石中存在微裂纹，应力脉冲在传播时会发生衰减.小振幅弹性波在岩石中的衰减是指数式的，一般情况下可通过弹性波振幅的变化获得其衰减系数，关系式为[26]

(19)

式中:σ0表示初始位置的应力峰值，σ(xF)表示传到距初始位置xF处的应力峰值，β为衰减系数.

首先采用低强度应力波冲击岩杆，得到杆中部位置(5#应变片，距入射端为0.6 m)应变信号，见图10(纵坐标为电压，横坐标为时间).由相邻拉应力波峰值时间差与杆长，求出波速c为2 740 m· s-1，则传播距离x可由x=ct得出.利用图10前5个拉应力波峰值拟合得出式(19)中的衰减系数β=0.52 m-1.

加大应力波强度，使得岩杆发生层裂，见图9(b)，测得其断裂面距加载端为0.79 m.按照镜像法，不考虑衰减效应，利用5#应变片信号，可得到不同时刻自由面附近的应力波形，见图11(纵坐标为轴向应力，横坐标表示杆件尾部位置).然后根据断裂位置找出该点的最大拉应力，就能确定“名义”层裂强度为σ0= 25.5 MPa.考虑压应力波由5#应变片位置传至自由端形成的拉应力波，再到断裂位置这一过程的衰减(传播距离x=(0.39+0.20)=0.59 m)，修正后得出层裂强度σt=25.5e-0.52×0.59=18.8 MPa.

图9　花岗岩杆层裂前后照片

图10　应力波衰减过程

将应力脉冲作为边界条件代入PD计算程序，其中Δx=0.01 m，Δt=2 μs.根据层裂强度，设定临界伸长率s0=σt/E= 0.000 95.考虑3种方法求解：

1)采用δ=3Δx的PD法进行计算；

2)先采用δ=Δx的PD法进行计算，当最大连接键伸长率smax= 0.9s0时，再令δ=3Δx计算；

3)先采用FDM法进行计算，当最大连接键伸长率smax= 0.9s0时，再用δ=3Δx的PD法计算.

以上3种方法分别记为：PD3，PD1-PD3和FDM-PD3，得出的断裂时间和计算耗时见表2，岩杆断裂时损伤情况见图12(纵坐标为损伤，横坐标表示杆件尾部位置).由表2看出，采用FDM-PD3求解耗时最少，PD3耗时最多.PD1-PD3和FDM-PD3得出的断裂时间接近，而PD3得出的断裂时间较大，这也反映了影响域增大，频散加重的特点.由图12可看出，杆0.79 m处发生断裂，与试验断裂位置一致，表明该方法能很好模拟杆中拉伸波导致的岩石层裂现象.文章提出的FDM和PD联合算法耗时少，精度高，有利于提高PD法对断裂问题的计算效率.

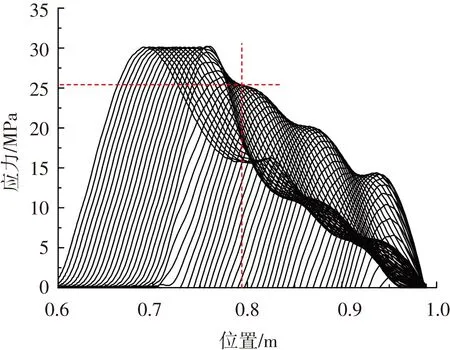
图11　应力波形叠加

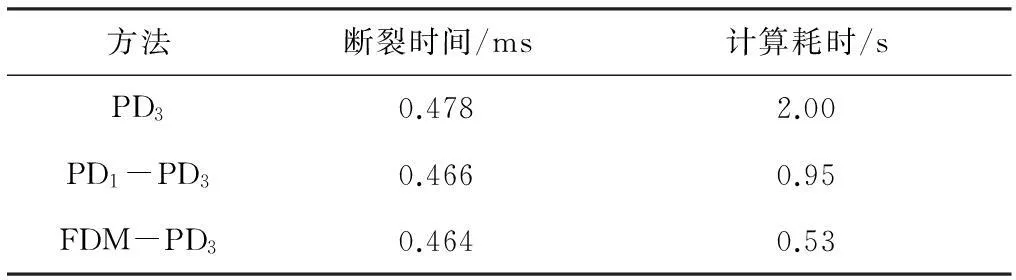
方法断裂时间/ms计算耗时/sPD30.4782.00PD1-PD30.4660.95FDM-PD30.4640.53

图12　岩杆断裂时损伤分布

4结论

研发了近场动力学法计算程序，并详细分析了该算法频散特性的影响因素，以及对数值计算的影响，之后应用到一维应力波作用下岩杆层裂破坏问题计算分析中，得出如下结论：

1)当空间步长不变时，随影响域变大，PD法计算精度降低；影响域内节点数目不变时，空间步长越小，PD法精度会显著提高；同一影响域内节点分布越密集，精度也有所提高；满足计算稳定性条件的前提下，PD法对时间步长变化不敏感.

2)PD法的离散方程可看作是一系列差分方程的组合，其截断误差为O(δ2)，当影响域半径δ等于Δx时，PD算法与中心有限差分法等价，此时计算精度高.当影响域增大时，PD法对连续变形问题计算效果要差于有限差分法.

3)岩杆一维波动层裂模拟结果与试验结果吻合度高.该方法简单易行，通过选择合适的计算参数压制数值频散，能很好地仿真出岩石拉伸波损伤发展演化直至断裂破坏的全过程，将FDM和PD法两者结合用于脆性材料损伤问题的分析，计算时间少，精度高，能够发挥各自优势，提高计算效率.

参考文献

[1] MADENCI E, OTERKUS E. Peridynamic theory and its applications[M]. New York: Springer-Verlag New York Inc, 2013.

[2] SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1):175-209.

[3] SILLING S A, ZIMMERMANN M, ABEYARATNE R. Deformation of a peridynamic bar[J]. Journal of Elasticity, 2003, 73(1/2/3):173-190.

[4] SILLING S A, ASKARI E. A meshfree method based on the peridynamic model of solid mechanics[J]. Computers & Structures, 2005, 83:1526-1535.

[5] HA Y D, BOBARU F. Studies of dynamic crack propagation and crack branching with peridynamics [J]. International Journal of Fracture, 2010, 162(1/2):229-244.

[6] HA Y D, BOBARU F. Characteristics of dynamic brittle fracture captured with peridynamics[J]. Engineering Fracture Mechanics, 2011, 78(6):1156-1168.

[7] WILDMAN R A, GAZONAS G A. A perfectly matched layer for peridynamics in two dimensions[J]. Journal of Mechanics of Materials and Structures 7(8):765-781.

[8] FOSTER J T, SILLING S A, CHEN W W. Viscoplasticity using peridynamics[J]. International Journal for Numerical Methods in Engineering, 2010, 81(10):1242-1258.

[9] HUANG Dan, ZHANG Qing, QIAO Pizhong. Damage and progressive failure of concrete structures using non-local peridynamic modeling[J]. Science China: Technological Sciences, 2011, 54 (3):591-596.

[10]沈峰, 章青, 黄丹，等. 基于近场动力学理论的混凝土轴拉破坏过程模拟[J].计算力学学报, 2013(增1):79-83.

[11] LIU W, HONG J W. Discretized peridynamics for linear elastic solids [J]. Computational Mechanics, 2012, 50(5):579-590.

[12]PARKS M L, PLIMPTON S J, LEHOUCQ R B, et al. Peridynamics with LAMMPS: A user guide, 2008-1035[R]. Albuquerque: Sandia National Laboratories, 2008.

[13]WECKNER O, ABEYARATNE R. The effect of long-range forces on the dynamics of a bar[J]. Journal of the Mechanics and Physics of Solids, 2005, 53(3):705-728.

[14]杨顶辉, 滕吉文. 各向异性介质中三分量地震记录的FCT有限差分模拟[J]. 石油地球物理勘探, 1997, (2):181-190.

[15]吴国忱, 王华忠. 波场模拟中的数值频散分析与校正策略[J]. 地球物理学进展, 2005, 20(1):58-65.

[16]刘东甲. 完整桩瞬态纵向振动的模拟计算[J]. 合肥工业大学学报(自然科学版)，2000，23(5): 683-687.

[17]柯宅邦, 刘东甲. 低应变反射波法测桩的轴对称问题数值计算[J]. 岩土工程学报, 2006, 28(12):2111-2115.

[18]卢志堂, 刘东甲, 龙丽丽, 等. 基桩低应变检测三维问题的数值计算[J]. 合肥工业大学学报(自然科学版)，2011，34(6):905-909.

[19]卢志堂, 王志亮, 刘东甲，等. 管桩低应变检测中的三维效应分析[J]. 同济大学学报(自然科学版), 2012, 40(11):1603-1607.

[20] 王礼立. 应力波基础[M]. 北京: 国防工业出版社, 2005:1-152.

[21]KLEPACZHO J R, BRARA A. An experiment method for dynamic tensile testing of concrete by spalling[J]. International Journal of Impact Engineering, 2001，25 (4):387-409.

[22]胡时胜, 张磊, 武海军, 等. 混凝土材料层裂强度的实验研究[J].工程力学, 2004, 21 (4):128-132.

[23]BRARA A, KLEPACZKO J R. Experimental characterization of concrete in dynamic tension[J]. Mechanics of Materials, 2006, 38(3):253-267.

[24]李夕兵, 陶明, 宫凤强,等. 冲击载荷作用下硬岩层裂破坏的理论和试验研究[J]. 岩石力学与工程学报, 2011, 30(6):1081-1088.

[25] WANG Zhiliang, ZHOU Nianqing, WANG Jianguo. Using Hopkinson pressure bar to perform dynamic tensile tests on SFRC at medium strain rates[J]. Magazine of Concrete Research, 2012, 64 (8):657-664.

[26]王志亮, 李洋, 阳栋. C75混凝土动态层裂强度试验研究[J]. 建筑材料学报, 2014, 17 (4):695-699.

[27]WANG ZhiLiang, YANG Dong. Study on dynamic behavior and tensile strength of concrete using 1D wave propagation characteristics[J]. Mechanics of Advanced Materials and Structures, 2015, 22(3):829-836.

(编辑赵丽莹)

Dispersion characteristics of peridynamics method and its application to spalling analysis of rock

LU Zhitang1, WANG Zhiliang1,2

(1.Department of Geotechnical Engineering，Tongji University，200092 Shanghai，China；2.School of Civil & Hydraulic Engineering, Hefei University of Technology, 230009 Hefei, China)

Abstract:The dispersion characteristics of PD is carried out to figure out the accuracy of peridynamics method (PD) and its simulation effects on rock spalling. Firstly, based on the dispersion analyses of the PD discrete equations, it is found that the numerical dispersion is more apparent with increasing the domain size if the space step is fixed; with the number of nodes in the domain fixed, the numerical dispersion becomes weaker when the space step decreases; the numerical dispersion also gets weaker with the increase of the nodes at a fixed domain. Subsequently, by comparing it to the traditional finite difference method, it is pointed out that the PD discrete equations can be written as the combination of a series of differential equations, whose truncation error is the second order infinitesimal of the domain radius (δ); when δ is set as the space step, PD method is equivalent to the central difference method, owning the highest calculational accuracy. Finally, the PD method is used to explore the one-dimensional spalling phenomenon of rock bar. The effects of space step and domain size on computing results are discussed, and the spalling time, spalling locations and damage distribution are further given. The effectiveness of PD method is also verified by contrast with the spalling test. It is shown that PD can be used for rock spalling analysis and high-precision results can be obtained by PD method coupled with FDM, costing less time and owning a clear advantage.

Keywords:peridynamics；dispersion characteristics；finite differential method；rock bar；spalling

中图分类号:TU45

文献标志码:A

文章编号:0367-6234(2016)02-0131-07

通信作者:王志亮,cvewzL@tongji.edu.cn.

作者简介:卢志堂(1985—)，男，博士研究生;王志亮(1969—)，男，教授，博士生导师.

基金项目:国家自然科学基金 (51174145，51379147，51579062)；

收稿日期:2015-06-23.

doi：10.11918/j.issn.0367-6234.2016.02.022

教育部博士点专项资金(20120072110024).