六点三重插值细分法

朱洪（安徽三联学院　基础部，安徽　合肥　230009）



六点三重插值细分法

朱洪
（安徽三联学院基础部，安徽合肥230009）

摘要：本文提出了双参数六点三重插值细分算法.利用生成多项式的方法分析了该算法的一致收敛和连续性条件，通过对参数的适当取值，极限曲线可达到C1,C2连续.数值算例表明，该方法是合理有效的.

关键词：三重细分法；插值；生成多项式；连续性

细分法是根据初始控制多边形或者初始数据由计算机生成曲线曲面或其他几何形体的一种方法，其处理方法简单而且易于实现，因此在曲线曲面造型中得到了广泛的应用.Dyn等[1]首次提出了只含一个参数的四点二重插值细分法（C1连续）.Hassan等[2]给出了四点三重插值细分算法（C2连续）.WANG Huawei等[3]提出了一种改进的三重插值细分算法，可以插值于开的控制多边形，极限曲线仍可以达到连续.Cavaretta A S等[4]对稳定细分法作了系统地研究.Rehan等[5]给出了一类三重细分算法，三点三重细分法（C1连续）和四点三重细分法（C2连续）.Siddiqi等[6]利用双曲函数，提出了动态的六点二重细分算法.本文提出了双参数的六点三重插值细分算法，利用生成多项式的方法讨论了此算法的一致收敛性和C1，C2连续性条件.

1　预备知识

给定初始控制点集P0={pi0∈Rd|i∈￠}，记Pk={pik∈Rd|i∈￠}为第k次细分后的控制点集，则三重细分法的生成规则为

其中α={ai|i∈￠}为此细分法的掩模，并将其记为S，则S的生成多项式为

定理1[2]若三重细分法A一致收敛，则掩模α={ai}满足

定理2[2]设三重细分法S的掩模α={ai}满足式（2），则存在一个三重细分法S1，满足

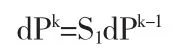
定理3[4]若三重细分法S的掩模α={ai}和Sj(j=1,2,…, n)的掩模α(j)={ai(j)}满足

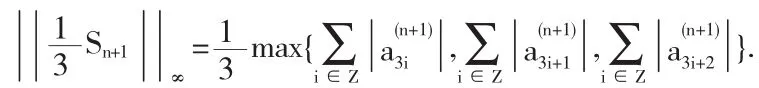
2　双参数六点三重插值细分法及收敛性和Ck连续性分析

定义1给定初始控制点集P0= {pi0∈Rd|i∈￠}，记Pk= {pik∈Rd|i∈￠}为第k次细分后的控制点集，递归地定义第k+1次细分后的控制点如下：

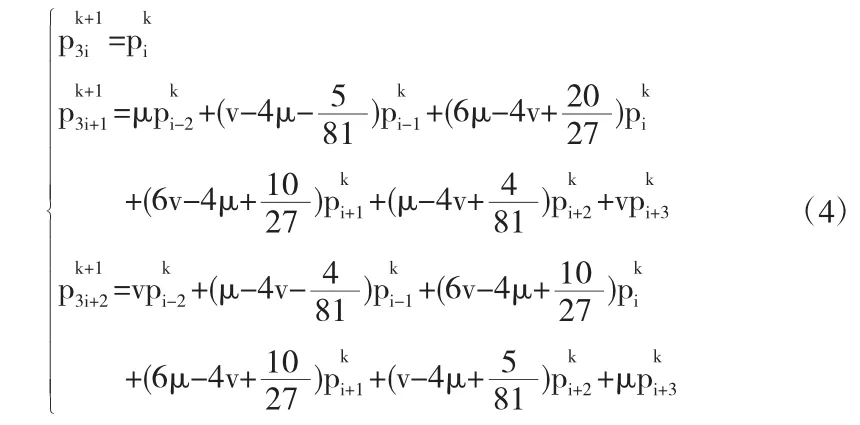
其中μ，v为参数.

下面利用定理[2]和定理[3]分析细分格式（4）的收敛性和Ck连续性.

定理4若参数μ，v满足：

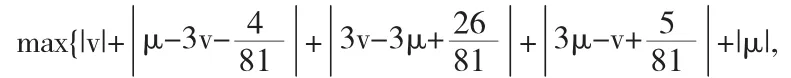
证明由细分格式（4）知该细分格式的生成多项式为：

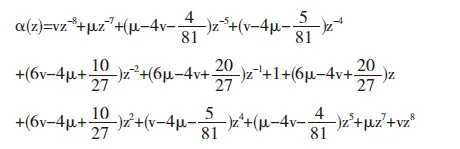
显然α满足（2）式.根据定理2知，

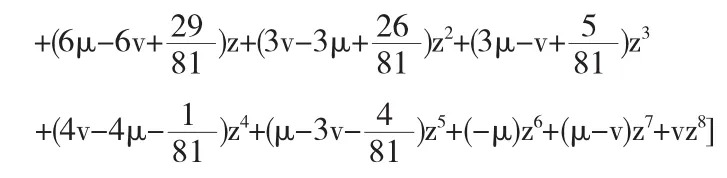
因此，当

时，此细分法是一致收敛的.

定理5若参数μ，v满足：

时，此细分法是C1连续的.

证明显然α，α(1)满足（3）式，且

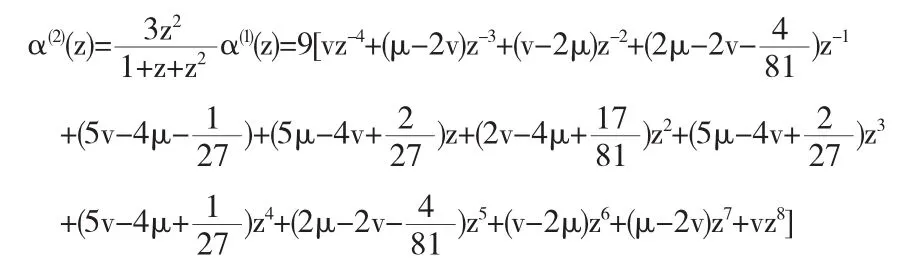
因此，当

时，此细分法是C1连续的.

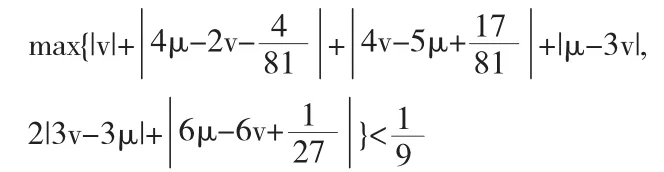
时，此细分法是C2连续的.

证明显然α，α(1)，α(2)满足（3）式，且

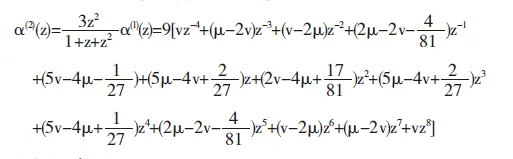
因此，当

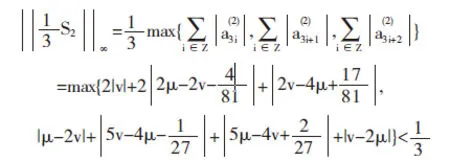
时，此细分法是C2连续的.

3　结论和数值实验

本文在文献[2]基础上给出了双参数六点三重插值细分算法，点数及参数的增加，使得对曲线的调控更加地灵活.下面给出几何造型曲线的实例，利用本文方法，经过六次细分，得到了C1,C2连续曲线，其中实线为细分曲线，虚线为初始控制多边形，如图1所示.

图1　六点三重插值细分法

该算法具有更高的细分效率，通过对比发现，对同一控制多边形，本文方法经过五次细分与文献[2]方法经过十次细分具有相同的曲线，如图2所示.

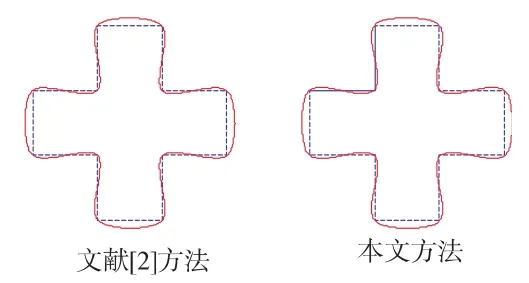
图2　对比算法

固定参数μ而改变另一参数v对极限曲线的影响，可发现，当固定参数μ，参数v在一定范围内从大到小变化时，曲线是先向外插值，再向内插值，同时向内微缩，如图3所示.固定参数v而改变另一参数μ，发现对极限曲线有类似的影响，如图4所示.

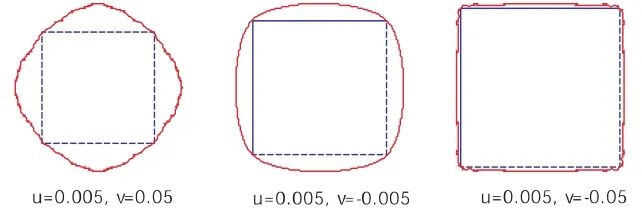
图3　参数v对极限曲线的影响

图4　参数μ对极限曲线的影响

当参数取某些特殊值时会有分形现象出现，如图5所示.因此，多点分形性质有待进一步研究.

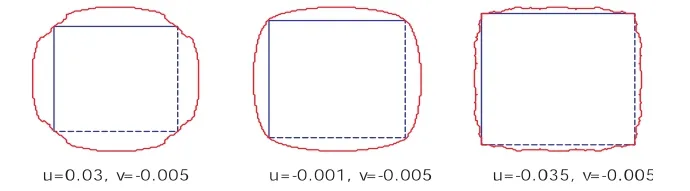
图5　分形现象

参考文献：

〔1〕Dyn N.Levin D, Gregory J A. A 4-point interpolatory subdivision scheme for curve design [J]. Computer Aided Geometric Design, 1987,4(4):257-268.

〔2〕Hassan M F, Ivrissimitzis I P, Dodgson N A, Sabin M A. An interpolating 4 -point ternary stationary subdivision scheme [J]. Computer Aided Geometric Design,2002,19(1):1-18.

〔3〕WANG Huawei, QIN Kaihuai. Improved Ternary Subdivision Interpolation Scheme [J]. TSINGHUA SCIENCE AND TECHNOLOGY,2005,10(1):128-132.

〔4〕Cavaretta A S, Dahmen W, Micchelli C A. Stationary subdivision [J]. Memoirs of the American Mathematical Society,1991,93(453):1-186.

〔5〕Rehan K, Siddiqi S S. A family of ternary subdivision scheme for curves [J]. Applied Mathematics and Computation, 2015:114-123.

〔6〕Siddiqi S S, Salam W, Rehan K. A new non-stationary binary 6 -point subdivision scheme [J]. Applied Mathematics and Computation, 2015: 1227-1239.

基金项目:安徽三联学院校级自然科学基金（2014Z002）

收稿日期：2015-11-05

中图分类号：TP391

文献标识码：A

文章编号：1673-260X（2016）01-0041-02