基于振动信号二维特征向量的配变铁心故障诊断

魏晓莹　宋仕江　郭谋发　卢国仪（. 福州大学电气工程与自动化学院，福州　50000；. 国网福建省电力有限公司邵武市供电公司，福建 邵武　54000；. 福州市城市地铁有限责任公司，福州　50000）



基于振动信号二维特征向量的配变铁心故障诊断

魏晓莹1宋仕江2郭谋发1卢国仪3
（1. 福州大学电气工程与自动化学院，福州350000；2. 国网福建省电力有限公司邵武市供电公司，福建 邵武354000；3. 福州市城市地铁有限责任公司，福州350000）

摘要配电变压器油箱表面蕴含着丰富的铁心振动信号，能够直接体现铁心的工作状况。通过希尔伯特黄（Hilbert-Huang Transform，HHT）带通滤波提取配电变压器铁心振动信号主成分，而后利用HHT二次带通滤波对配变铁心振动信号进行时频分解，分别求取各子频带所对应的能量值和重心频率，构成振动信号的二维特征向量。通过空载试验测得配变铁心在铁心正常、两点接地、铁心松动、接地不良等4种典型情况下的振动信号，对所测多组振动信号的二维特征向量做SVM分类。结果表明该特征向量能够准确、有效地表征配变铁心的各种状态。

关键词：配变铁心；振动信号；HHT带通滤波；二维特征向量；RBF_SVM

The Fault Identification Method for Distribution Transformer based on Support Vector Machine Classification of Vibration Signal Characteristics

Wei Xiaoying1Song Shijiang2Guo Moufa1Lu Guoyi3
（1. College of Electrical Engineering and Automation， Fuzhou University， Fuzhou350000;
2. Shaowu Electric Power Supply Company， State Grid Fujian Electric Power Co.， Ltd， Shaowu， Fujian354000; 3. Fuzhou Metro Co.， Ltd， Fuzhou350000）

Abstract The tank surface of distribution transformer contains a wealth of vibration signals from the iron core， which can directly reflect the working conditions of the core. Extracting the principal component of the core from vibration signals via Hilbert-Huang Transform （HHT） band-pass filter， and then the vibration signal is decomposed in time-frequency domain via the second band-pass filter of HHT， calculating the energy and center frequency of each sub-band reconstructed signal， which constitute the 2-D feature vector of the vibration signal. The vibration signal of the core in 4 typical conditions including normal states， two-point grounding， looseness and poor grounding are measured through no-load experiment， SVM classification is applied to these 2-D feature vectors. The result shows that the feature vector can represent each state of the core accurately and effectively.

Keywords：the core of distribution transformer; vibration signal; HHT band-pass filter; 2-D feature vector; RBF_SVM

铁心是配电变压器（以下简称配变）中传递、交换电磁能量的主要部件，对配变的电磁性能、机械强度等有着举足轻重的作用。统计资料表明，因铁心问题造成故障，占变压器总事故中的第三位[1]。配变运行时其油箱表面蕴含着丰富的振动信号，该信号主要由铁心和绕组所产生的振动混叠而成，铁心状态的改变将导致振动信号的变化。因此，配变振动信号的有效特征量可用于铁心各种状态的识别。

振动信号的处理包括信号分离和特征提取。信号分离主要采用盲源分离方法[2]。由于配变的振动信号来自多个振源，盲源分离算法能实现某种程度的信号分离，但存在着频带混叠的现象。常用的特征提取方法有小波变换[3]、HHT[4-5]、局域均值分解（Local Mean Decomposition，LMD）[6]等。针对变压器油箱表面不同测点的振动信号，文献[3]提出基于交叉小波变换的方法，在时频域上分析不同测点振动信号间的相关性。文献[5]通过希尔伯特变换得到希尔伯特边际谱与能量谱，最后利用获得的两个图谱揭示正常运行和有潜伏性故障的铁心振动特征。文献[6]运用LMD将振动信号自适应地分解为一系列单分量调幅-调频信号，表征铁心振动特征。以上特征提取方法均为一维特征量，缺乏一定的可靠性和准确性。

基于此，本文提出了利用HHT带通滤波的方法，分离出能够表征铁心振动特征的信号，采用能量和重心频率构成的二维特征向量作为故障诊断的依据，最后通过粒子群优化支持向量机进行铁心状态的分类，为配变铁心的在线诊断提供了一种有效的方法。

1　配电变压器振动原理

配变油箱表面的振动主要是由铁心和绕组引起的，其中铁心振动主要是由硅钢片的磁致伸缩效应引起的，绕组振动主要是由于电流通过绕组产生了电磁力引起的。配变空载运行时没有负载电流，因此可以忽略绕组振动，认为油箱表面的振动信号即为铁心振动信号。

铁心的振动加速度与电压的平方呈线性正相关关系，其基频分量为所施加电压的2倍频。由于磁致伸缩与磁通密度的关系是非线性的，同时沿铁心内外边缘的磁路长短也不一致，因此铁心振动加速度信号除基频分量外，还含有高次谐波分量，而这些分量与电压的平方不存在线性关系[7]。

2　振动信号的提取和二维特征向量的求取方法

2.1基于HHT的振动信号特征频带提取

如果某个信号的采样点数为N，经过EMD后得到L个IMF分量，再进行Hilbert变换可得到一个二维Hilbert谱灰色图，该图含有L×N个数据点，反映着时间t内所有IMF分量对应的瞬时频率，其灰度值大小对应着该时刻上IMF瞬时幅值的大小。因此，在Hilbert谱图中可以根据瞬时频率的不同进行频带的划分。为了得到某个频带范围内的信号，只需将各IMF分量在该频带范围外的幅值置零，然后对处理过的IMF分量进行重构，所得到的重构信号即为原始信号在该频带范围内的分量，以上即为HHT带通滤波的原理[8]。

2.2二维特征向量的求取方法

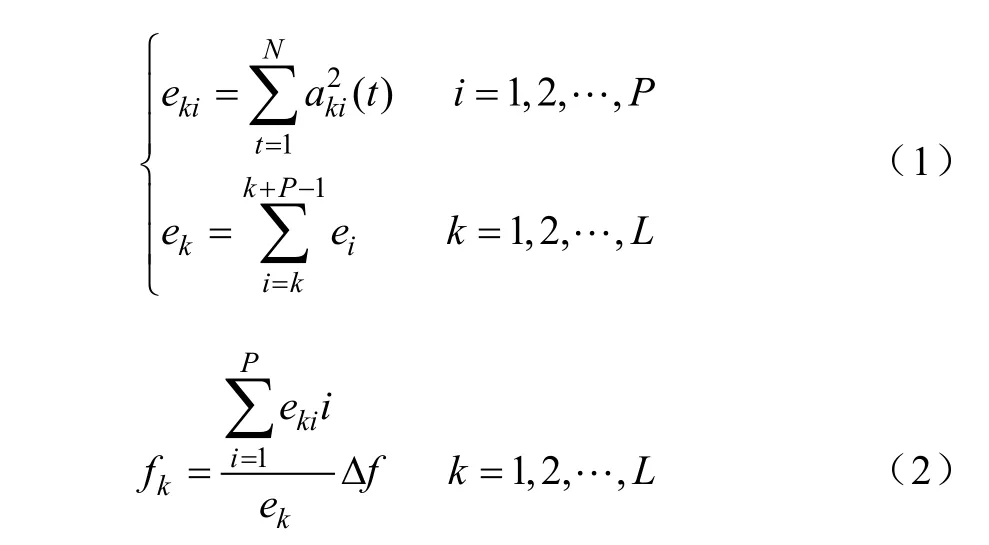
式中，ek、fk分别为第k个一次重构频带的能量值和重心频率。eki为第k个一次重构频带所对应的第i个子频带的能量值。假设有l个振动信号，由此可得这些振动信号构成的能量值矩阵如式（3）所示，重心频率矩阵如式（4）所示。

为更好地将振动信号二维特征向量进行比较，需对能量和重心频率归一化，具体处理分别如式（5）、（6）所示。

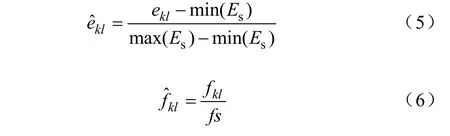
式中，ekl为Es中的元素，min（Es）为Es元素中的最小值，max（Es）为Es元素中的最大值；fkl为Fg中的元素，fs为振动信号的采样频率。将归一化后的能量和重心频率按式（7）交叉排序，构成一个二维特征向量矩阵作为配变铁心状态诊断的特征量。

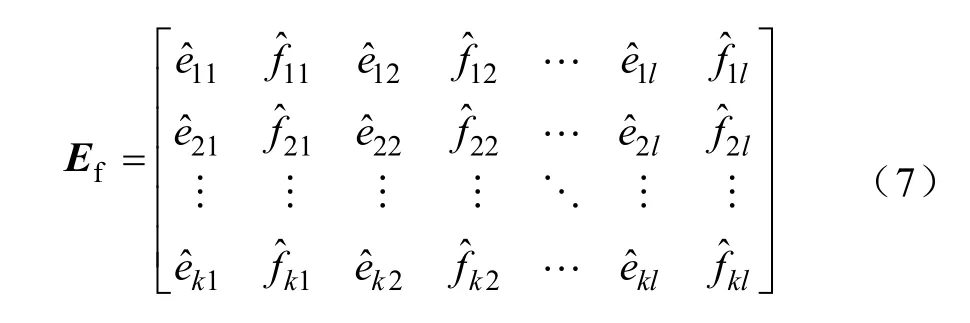
相比于仅用一个特征量表征铁心振动信号，二维特征向量所包含的能量和重心频率互为补充，增加了诊断的准确性和可靠性。

3　配电变压器铁心振动信号的采集和特征量的提取

3.1配电变压器振动采集试验

配变振动信号采集系统由加速度传感器、振动信号采集装置及上位机软件组成，如图1所示。

图1　配变振动信号采集系统

采用型号为LC0156A的压电式加速度传感器，其频率响应范围为0.1～2000Hz，灵敏度为1491mV/g （g为重力加速度），量程为0～±3g，分辨率为0.00002g；振动信号采集装置选用NI USB-6218模块搭建；上位机软件由Matlab和LabVIEW混合编程开发。

为避免高压侧的强磁干扰且考虑到安全性问题，测点宜选在低压侧。试验研究表明，低压侧中部的位置蕴含较大能量，可较好地反映变压器的振动特性。本文试验所选测点对应于低压侧A、B、C三相绕组，且位于油箱的中部，分别定义为测点1、测点2、测点3。

由铁心振动原理可知，负载电流对铁心振动没有直接的影响，因此可以基于空载试验模拟配变铁心正常工作、两点接地、铁心松动、接地不良等情况。选取型号为S11-M-315/10的配电变压器在其空载时做以上四种试验，如图2所示。

图2　配变铁心故障模拟

3.2基于HHT的铁心振动信号提取

在配变低压侧施加额定电压，模拟4种铁心运行状态。采集油箱表面的振动信号，以三个测点额定电压下不同运行状态为例，画出其频域柱状图，如图3所示。

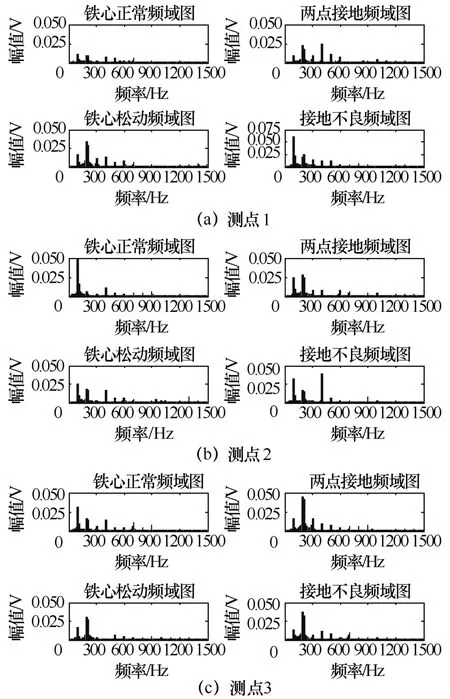
图3　空载额定电压时铁心不同状态下各测点振动信号频域图

从频域图可以看出，铁心振动信号主要集中在0～1000Hz，当频率大于1000Hz时其振幅几乎为0，可以忽略不计；另外，当铁心正常时，100Hz频率处的幅值为其振动的主要分量，在其他各频带的振动幅值较小；而发生故障时，振动信号含有大量的高频分量，由于模拟故障接地点在A相下方，因而在各测点的两点接地频域图中测点3振动幅值相对测点1、2较大。因此利用HHT带通滤波的方法分离出0～1000Hz频率成分作为表征铁心振动特性的信号。

3.3配电变压器铁心振动二维特征向量的提取

通过HHT带通滤波的信号分离方法可知，表征铁心振动特性的频率主要分布在0～1000Hz。对提取出的铁心振动信号进行一次HHT带通滤波，取频带间隔为100Hz得到一次重构分量。然后对每个带宽为100Hz的一次重构分量进行二次HHT带通滤波，取频带间隔为20Hz，则每个频带重构分量可划分为5个子频带。将这5个二次带通滤波重构信号根据式（2）、式（3）求出其所对应的一个能量值和一个重心频率。由于篇幅所限，本文仅列出测点3铁心4种状态下各取5个样本归一化后的能量值矩阵和重心频率矩阵，分别如式（8）、式（9）所示，每一行代表一个样本的特征值。

s 0 . 1 1 6 9　　0 . 0 5 1 0　　0 . 0 1 8 9　　0 . 0 0 9 7　　0 . 0 1 0 7　　0 . 0 1 1 3　　0 . 0 0 9 7　　0 . 0 0 7 2　　0 . 0 0 2 8　　0 . 0 0 1 3 0 . 1 3 1 5　　0 . 0 6 4 7　　0 . 0 2 5 2　　0 . 0 0 6 8　　0 . 0 0 8 7　　0 . 0 0 9 4　　0 . 0 0 7 4　　0 . 0 0 4 3　　0 . 0 0 2 2　　0 . 0 0 0 9 0 . 1 0 5 E ＝0　　0 . 0 4 4 9　　0 . 0 2 7 9　　0 . 0 0 5 5　　0 . 0 0 8 3　　0 . 0 1 0 9　　0 . 0 1 1 8　　0 . 0 0 5 4　　0 . 0 0 3 5　　0 . 0 0 0 9 0 . 1 1 2 1　　0 . 1 0 3 3　　0 . 0 2 0 3　　0 . 0 0 5 6　　0 . 0 0 6 7　　0 . 0 0 8 0　　0 . 0 1 1 9　　0 . 0 0 5 6　　0 . 0 0 2 3　　　　0 0 . 1 2 7 6　　0 . 0 5 6 7　　0 . 0 3 5 0　　0 . 0 1 4 3　　0 . 0 0 9 7　　0 . 0 0 9 6　　0 . 0 0 5 7　　0 . 0 0 5 0　　0 . 0 0 1 9　　0 . 0 0 1 1 0 . 1 3 7 8　　0 . 3 0 6 6　　0 . 1 6 5 0　　0 . 0 7 3 9　　0 . 0 9 7 1　　0 . 0 2 5 9　　0 . 0 1 5 7　　0 . 0 0 9 6　　0 . 0 0 8 2　　0 . 0 0 8 2 0 . 2 1 3 0　　0 . 2 3 3 5　　0 . 1 6 6 1　　0 . 0 7 8 9　　0 . 1 0 1 0　　0 . 0 1 6 1　　0 . 0 0 3 3　　0 . 0 0 0 4　　0 . 0 0 0 6　　0 . 0 0 0 5 0 . 1 3 4 8　　0 . 2 5 0 5　　0 . 1 7 6 0　　0 . 0 7 9 9　　0 . 0 7 9 4　　0 . 0 2 8 6　　0 . 0 1 5 3　　0 . 0 1 4 7　　0 . 0 1 1 1　　0 . 0 1 0 2 0 . 1 7 6 0　　0 . 2 7 0 2　　0 . 1 2 5 3　　0 . 0 8 0 5　　0 . 0 9 1 1　　0 . 0 3 2 1　　0 . 0 0 9 4　0 . 0 0 5 6　　0 . 0 0 5 2　　0 . 0 0 4 7 0 . 1 4 2 3　　0 . 2 7 0 4　　0 . 1 2 8 1　　0 . 0 6 7 7　　0 . 0 7 3 8　　0 . 0 3 4 0　　0 . 0 1 7 3　　0 . 0 0 5 8　　0 . 0 0 5 0　　0 . 0 0 5 1 0 . 1 4 2 2　　0 . 3 9 2 5　　0 . 2 6 2 9　　0 . 0 3 7 4　　0 . 0 2 1 1　　0 . 0 1 7 7　　0 . 0 0 9 5　　0 . 0 0 4 7　0 . 0 0 0 5　　0 . 0 0 0 7 0 . 1 5 0 4　　0 . 5 0 8 0　　0 . 2 1 1 0　　0 . 0 3 7 0　　0 . 0 3 2 7　　0 . 0 2 7 8　　0 . 0 2 4 1　　0 . 0 1 6 7　　0 . 0 1 2 7　　0 . 0 1 1 6 0 . 1 2 7 1　　0 . 5 1 1 4　　0 . 1 9 4 5　　0 . 0 3 6 1　　0 . 0 1 8 1　　0 . 0 1 2 9　　0 . 0 1 4 3　　0 . 0 0 6 2　　0 . 0 0 2 4　　0 . 0 0 1 9 0 . 1 0 0 2　　0 . 6 0 7 8　　0 . 2 1 1 4　　0 . 0 5 2 0　　0 . 0 1 8 6　　0 . 0 2 0 2　　0 . 0 1 9 2　　0 . 0 0 6 3　　0 . 0 0 6 0　　0 . 0 0 4 4 0 . 1 7 6 3　　0 . 4 7 4 2　　0 . 2 5 7 6　　0 . 0 6 9 3　　0 . 0 5 7 7　　0 . 0 4 6 5　　0 . 0 4 3 4　　0 . 0 3 7 0　　0 . 0 3 6 0　　0 . 0 3 5 7 0 . 7 8 5 9　　0 . 5 7 3 9　　0 . 1 8 4 2　　0 . 0 5 3 8　　0 . 0 3 6 9　　0 . 0 1 7 4　　0 . 0 1 2 9　　0 . 0 0 9 4　　0 . 0 0 7 7　　0 . 0 0 6 9 0 . 5 9 7 0　　0 . 6 8 3 6　　0 . 2 3 6 4　　0 . 0 6 0 5　　0 . 0 7 0 3　　0 . 0 5 9 4　　0 . 0 4 7 6　　0 . 0 4 5 0　　0 . 0 4 3 3　　0 . 0 4 2 3 0 . 4 7 8 9　　0 . 7 4 2 1　　0 . 2 6 4 2　　0 . 1 1 0 3　　0 . 1 0 3 5　　0 . 0 9 1 2　　0 . 0 8 6 7　　0 . 0 8 0 4　　0 . 0 7 9 2　　0 . 0 7 8 2 1 . 0 0 0 0　　0 . 5 0 8 4　　0 . 1 5 1 9　　0 . 0 3 0 8　　0 . 0 1 8 6　　0 . 0 1 2 9　　0 . 0 1 0 2　0 . 0 0 7 2　　0 . 0 0 4 7　　0 . 0 0 3 9 0 . 9 7 1 1　　0 . 7 1 3 9　　0 . 1 9 4 8　　0 . 1 2 9 4　　0 . 0 8 7 0　　0 . 0 8 4 0　　0 . 0 7 6 9　　0 . 0 7 4 3　　0 . 0 7 3 7　　0 . 0 7 3 0■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■（8 ）g 0 . 0 4 6 0　　0 . 0 5 9 5　　0 . 0 4 3 9　　0 . 0 6 6 6　　0 . 0 5 7 1　　0 . 0 6 1 5　　0 . 0 5 5 1　　0 . 0 5 4 9　　0 . 0 6 1 6　　0 . 0 5 5 4 0 . 0 5 1 0　　0 . 0 4 4 1　　0 . 0 4 5 2　　0 . 0 6 2 4　　0 . 0 5 6 8　　0 . 0 6 2 3　　0 . 0 5 7 1　　0 . 0 5 6 6　　0 . 0 5 5 4　　0 . 0 6 9 7 0 . 0 4 5 F ＝0　　0 . 0 6 1 4　　0 . 0 3 5 7　　0 . 0 7 2 6　　0 . 0 5 3 0　　0 . 0 6 1 3　　0 . 0 5 9 1　　0 . 0 5 8 7　　0 . 0 5 6 9　　0 . 0 5 8 0 0 . 0 4 4 8　　0 . 0 4 5 9　　0 . 0 3 9 2　　0 . 0 6 8 3　　0 . 0 5 9 9　　0 . 0 6 2 7　　0 . 0 5 8 1　　0 . 0 5 4 7　　0 . 0 5 1 2　　0 . 0 5 7 2 0 . 0 4 0 1　　0 . 0 6 0 1　　0 . 0 4 1 5　　0 . 0 6 1 2　　0 . 0 5 5 0　　0 . 0 6 2 8　　0 . 0 5 6 7　　0 . 0 5 6 3　　0 . 0 6 1 5　　0 . 0 5 7 9 0 . 0 4 9 5　　0 . 0 5 6 3　　0 . 0 4 7 6　　0 . 0 6 1 6　　0 . 0 5 4 6　　0 . 0 5 0 1　　0 . 0 5 6 0　　0 . 0 5 8 5　　0 . 0 6 2 0　　0 . 0 6 0 1 0 . 0 4 5 1　　0 . 0 5 7 8　　0 . 0 5 3 1　　0 . 0 5 5 1　　0 . 0 5 7 3　　0 . 0 4 5 3　　0 . 0 4 2 8　　0 . 0 5 7 5　　0 . 0 5 8 0　　0 . 0 5 9 6 0 . 0 4 6 7　　0 . 0 6 6 6　　0 . 0 5 1 1　　0 . 0 5 9 6　　0 . 0 5 7 5　　0 . 0 5 4 8　　0 . 0 5 6 2　　0 . 0 5 3 2　　0 . 0 5 9 8　　0 . 0 5 7 6 0 . 0 5 0 7　　0 . 0 5 5 7　　0 . 0 5 1 1　　0 . 0 6 2 3　　0 . 0 5 6 0　　0 . 0 5 1 8　　0 . 0 4 6 3　0 . 0 5 6 8　　0 . 0 5 7 1　　0 . 0 6 0 5 0 . 0 5 5 9　　0 . 0 6 0 4　　0 . 0 4 4 2　　0 . 0 6 9 2　　0 . 0 5 8 8　　0 . 0 5 1 9　　0 . 0 5 0 4　　0 . 0 5 8 8　　0 . 0 6 3 4　　0 . 0 5 7 3 0 . 0 4 1 3　　0 . 0 7 5 3　　0 . 0 4 2 6　　0 . 0 4 4 9　　0 . 0 5 8 3　　0 . 0 5 4 9　　0 . 0 5 7 4　　0 . 0 5 9 0　0 . 0 5 9 4　　0 . 0 5 7 3 0 . 0 5 5 9　　0 . 0 7 0 6　　0 . 0 3 9 2　　0 . 0 5 2 9　　0 . 0 6 0 1　　0 . 0 5 7 8　　0 . 0 5 6 6　　0 . 0 5 7 8　　0 . 0 6 0 5　　0 . 0 6 0 1 0 . 0 5 0 2　　0 . 0 6 8 5　　0 . 0 3 8 9　　0 . 0 4 5 5　　0 . 0 5 5 9　　0 . 0 6 0 6　　0 . 0 5 7 2　　0 . 0 4 8 3　　0 . 0 6 4 4　　0 . 0 5 9 3 0 . 0 3 4 4　　0 . 0 7 1 2　　0 . 0 4 0 8　　0 . 0 4 2 9　　0 . 0 5 9 0　　0 . 0 5 9 7　　0 . 0 5 4 7　　0 . 0 5 7 4　　0 . 0 5 9 1　　0 . 0 5 9 8 0 . 0 5 6 8　　0 . 0 6 9 6　　0 . 0 4 3 9　　0 . 0 5 3 5　　0 . 0 5 8 3　　0 . 0 5 9 6　　0 . 0 5 8 0　　0 . 0 5 9 1　　0 . 0 5 9 9　　0 . 0 0 0 2 0 . 0 8 3 6　　0 . 0 3 4 2　　0 . 0 4 6 7　　0 . 0 5 3 5　　0 . 0 6 3 0　　0 . 0 6 0 4　　0 . 0 5 9 1　　0 . 0 5 8 5　　0 . 0 5 8 6　　0 . 0 5 9 2 0 . 0 7 9 9　　0 . 0 3 2 9　　0 . 0 5 0 2　　0 . 0 5 7 3　　0 . 0 6 1 1　　0 . 0 5 5 1　　0 . 0 5 9 0　　0 . 0 5 9 8　　0 . 0 5 9 2　　0 . 0 5 9 9 0 . 0 8 0 8　　0 . 0 3 4 0　　0 . 0 5 1 3　　0 . 0 5 6 9　　0 . 0 5 9 1　　0 . 0 5 8 7　　0 . 0 5 9 2　　0 . 0 5 9 7　　0 . 0 5 9 9　　0 . 0 6 0 2 0 . 0 7 9 9　　0 . 0 3 3 0　　0 . 0 4 1 1　　0 . 0 5 5 7　　0 . 0 6 0 4　　0 . 0 5 6 6　　0 . 0 6 0 3　0 . 0 5 9 6　　0 . 0 5 5 6　　0 . 0 6 1 5 0 . 0 8 1 1　　0 . 0 4 1 7　　0 . 0 5 2 4　　0 . 0 5 7 7　　0 . 0 6 0 1　　0 . 0 5 8 5　　0 . 0 6 0 0　　0 . 0 5 9 6　　0 . 0 5 9 4　　0 . 0 5 9 9■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■（9 ）

以测点3铁心正常状态、两点接地、铁心松动、接地不良4种状态为例，各取5组数据计算其二维特征向量，画出散点分布图，分别如图4所示，用5种颜色的圆圈区别各组数据。

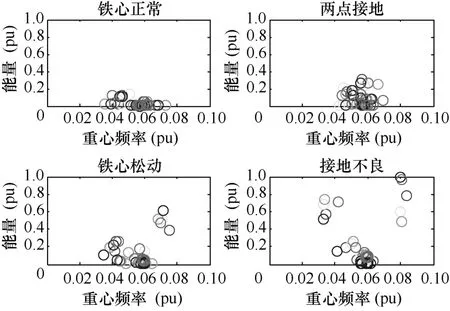
图4　二维特征向量分布图

从图中可以看出，铁心同一状态的5个样本分布大致相同；但不同状态所对应的二维特征向量分布有明显区别，各频段的重心频率和能量值大小均有显著差异。铁心正常时重心频率分布均匀且能量值较低；发生两点接地故障时，其能量值略高于正常情况，且重心频率较为集中；铁心松动时，在重心频率较大处的能量值也较大；而发生接地不良故障时，在重心频率较高和较低处的能量值均较高。二维特征向量同时反映了铁心振动信号能量值大小和能量谱重心位置的变化，二者互为补充，能够较为全面地描述振动信号的时频特性。

4　基于支持向量机的配变铁心状态诊断

4.1基于PSO优化的RBF核支持向量机

SVM是建立在统计学习理论和结构风险最小化原则基础上发展而来的学习机器，通过核函数的引入，可以把非线性空间的问题映射到高维线性空间解决，降低了算法的复杂度。SVM不论对小样本、非线性或是高维度模式识别都具有较好的效果。选用在缺乏问题先验知识的情况下适应性最好的RBF核作为SVM的核函数。在RBF核SVM的训练中，其主要性能受核参数σ 和惩罚参数C的影响，为了寻找最优参数，本文采用粒子群优化方法，该方法相对于遗传算法和网格法具有收敛快、准确率高等优点[10]。

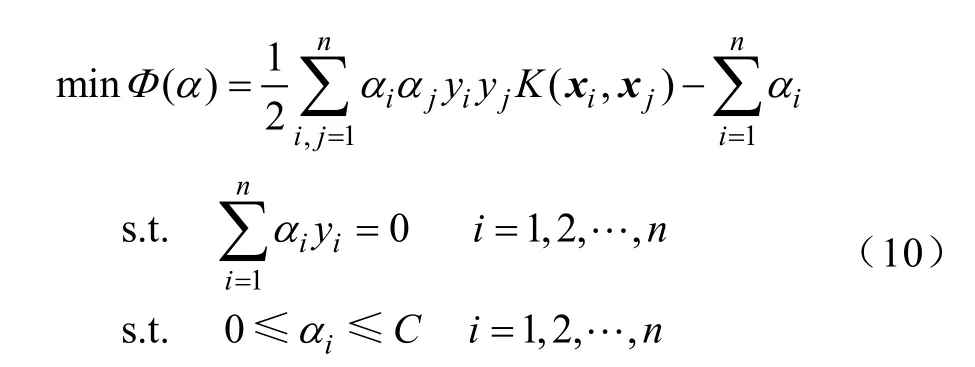
式中，C为惩罚参数，αi为拉格朗日乘子，将上述问题转化为对偶问题，求得对应的分类决策函数为

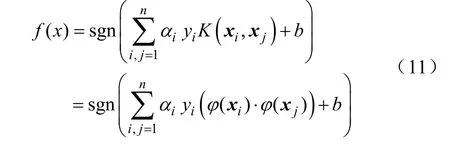
式中，K（ xi， xj）为核函数，RBF核函数的表达式为

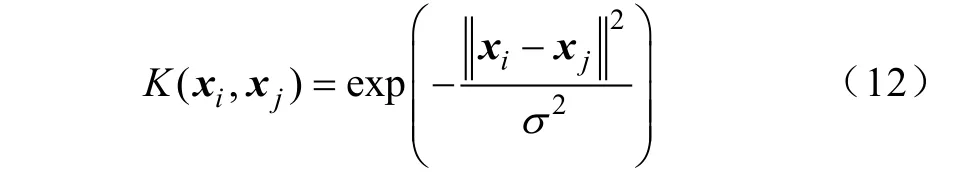
4.2配变铁心的支持向量机状态诊断

首先，利用实验室试验所测的配变油箱表面振动信号数据，提取铁心不同状态所对应的二维特征向量各50组；然后将这50组特征量随机均分为两组，取其中一组作为训练样本，另一组作为测试样本。定义类别标签为：①代表铁心正常；②代表两点接地；③代表铁心松动；④代表接地不良。通过PSO对训练样本的训练进行参数优化，得到各测点的最优核函数参数和最优惩罚参数，见表1。

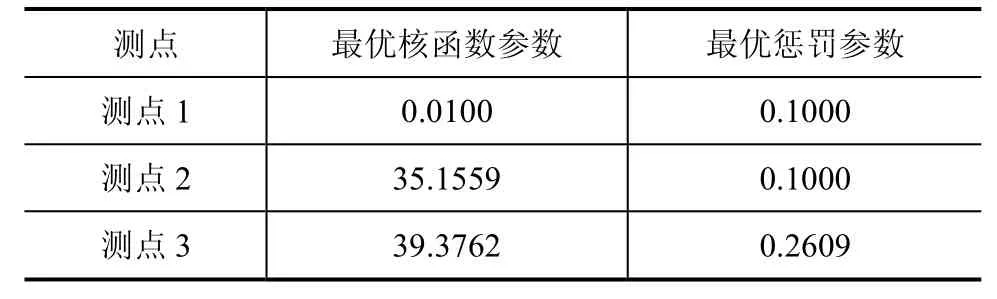
表1　各测点参数寻优结果

从表1可以看出，不同测点通过寻优求得的参数值有所不同，表明了在同一水平面不同相之间的振动特性差异较大。

通过PSO寻优确定最优σ和C后，即可对样本进行分类。分别输入各测点的训练样本和测试样本以及各自的类别标签，依次对各测点进行SVM。同样以测点3为例，画出其各测试样本的分类情况，如图5所示，用不同的图形及颜色来代表铁心各种运行状态，以便于区分。各测点分类结果见表2。

从图表中可以看出，SVM的结果验证了所提取特征量能够可靠并有效地表征配变铁心故障状态。

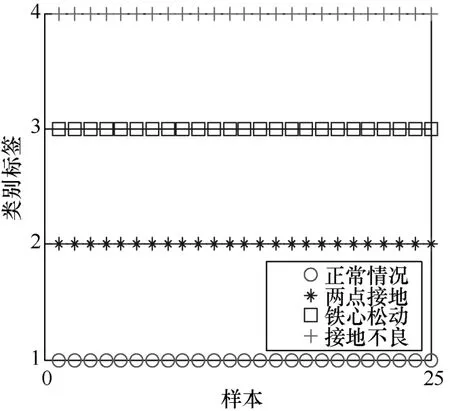
图5　测点3分类结果

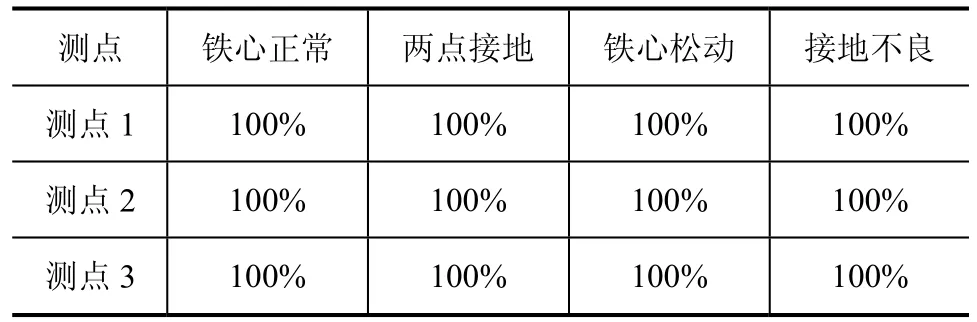
表2　各测点铁心待测样本集分类准确率

5　结论

运用HHT带通滤波得到能够表征铁心振动特性的特征频带，进而计算其能量及重心频率作为铁心的二维特征向量，最后利用PSO优化的RBF_SVM对铁心不同状态进行分类。理论分析和大量试验表明：

1）通过空载试验能够准确检测出铁心存在的各种隐患及故障，利用HHT带通滤波与重构可提取表征铁心振动特性的信号特征。

2）利用振动信号能量和重心频率构造二维特征向量，二者相互补充，较为全面地体现振动信号的特征，为故障诊断的可靠性和准确率奠定了基础。

3）通过PSO优化的SVM进行分类，验证了二维特征向量的有效性，其分类准确率高，并且能够解决小样本问题。

参考文献

[1]郑婧， 王婧（頔）， 郭洁， 等. 电力变压器铁心振动特性分析[J]. 电子测量与仪器学报， 2010， 24（8）: 763-768.

[2]郭俊， 汲胜昌， 沈琪， 等. 盲源分离技术在振动法检测变压器故障中的应用[J]. 电工技术学报， 2012，27（10）: 68-78.

[3]王峰， 苑津莎， 李中. 基于交叉小波变换的变压器振动信号分析[J]. 电工电能新技术， 2014， 33（4）: 36-40， 75.

[4]Huang Ne， Shen Z， Long Sr. A new view of nonlinear water waves[J]. Annual Review of Fluid Mechanics，1999， 31（1）: 417-457.

[5]熊卫华， 赵光宙. 基于希尔伯特-黄变换的变压器铁心振动特性分析[J]. 电工技术学报， 2006， 21（8）: 9-13.

[6]李纯子， 陈峰， 刘书成， 等. 基于小波变换和LMD算法的变压器振动信号分析[J]. 电工电能新技术，2013， 32（4）: 69-73， 78.

[7]徐志. 基于振动法的变压器在线监测研究[D]. 重庆:重庆大学， 2010.

[8]郭谋发， 徐丽兰， 缪希仁， 等. 采用时频矩阵奇异值分解的配电开关振动信号特征量提取方法[J]. 中国电机工程学报， 2014， 34（28）: 4990-4997.

[9]肖先勇， 张文海， 汪颖， 等. 基于故障相暂态信号特征的二维故障选线法[J]. 电网技术， 2012， 36（5）: 178-184.

[10]费胜巍， 苗玉彬， 刘成良， 等. 基于粒子群优化支持向量机的变压器故障诊断[J]. 高电压技术， 2009（3）: 509-513.

魏晓莹（1992-），硕士研究生，主要研究方向为配电网自动化。

作者简介