基于阶次分析的风机增速箱故障诊断
陈长征,王海童,孙自强
(沈阳工业大学 机械工程学院,辽宁 沈阳 110178)
·故障诊断·
基于阶次分析的风机增速箱故障诊断
陈长征,王海童,孙自强
(沈阳工业大学 机械工程学院,辽宁 沈阳 110178)
风力发电机组工作环境恶劣,振动信号往往具有非平稳的特性。为了提取故障信息的特征频率,提出了基于重采样的阶次分析和小波阈值去噪相结合的诊断方法。该方法与经典的计算阶次跟踪算法(COT)相比较,提高了重采样精度,与传统的FFT方法相比较,消除了因转速不稳定引起的“频率模糊”现象。并通过风场实验表明该方法有效,具有工程应有价值。
风力发电机;小波去噪;阶次分析;重采样
0 前言
齿轮箱作为风机最主要的结构之一,其发生故障的频率最高,造成的停机时间也最长。同时由于受风机自身结构和风速时刻变化的双重影响,所采集到风机齿轮箱的故障信号往往具有非平稳的特性,而传统的基于FFT的普通频谱分析方法只能提取机械在转速稳定状况下的特征频率。若将此方法用于提取风机故障时的特征频率,则将出现难以辨认的“频率模糊”现象[1-6]。阶次分析是以角域采样的理论为基础建立起来的,其重要的思想就是将振动信号从时域转换到角域,因此阶次分析的关键技术就是实现等角度采样[7]。要实现对风机旋转不稳定状态下的角域采样,可利用阶次跟踪的方法,常用的阶次跟踪方法有两种:一种是硬件阶次跟踪方法,一种是计算阶次跟踪方法[8]。硬件阶次跟踪不仅成本高而且在风机上安装比较困难。计算阶次跟踪可利用数值插值的方法实现角域采样,降低了成本。而基于等角度重采样的阶次分析是最常用的一种阶次跟踪方法但在实际工程中,由于受各种因素的影响,所采集到振动信号信息不可避免的会存在各种噪声,从而会影响重采样的精度,本文采用小波硬阈值去噪的方法对其重采样后的角域信号进行去噪处理,再进行FFT变换得到阶次谱,通过和经典的阶次跟踪方法(COT)相比较,提高了其重采样精度。
1 基于阶次分析和小波阈值去噪处理非平稳信号的原理
1.1 阶次分析和经典的计算阶次跟踪(COT)
(1)
式中,O为阶次;F为振动信号的频率;n为参考轴的转速。
为了能得到等间隔角度的时间采样点,假定在短时间内,转轴的角加速度是保持不变的,转过的角度和时间的关系可表示为
φ(t)=b0+b1t+b2t2
式中,t为时间点;并假设每2个脉冲之间的相位差为Δφ;b0~b2表示未知系数,则
由式(2)、式(3)可得
(4)
式中,Δφ为采样角度;k为插值系数,其与采样阶次之间的关系为
(5)
根据式(4)求出的时间点,可得到等角度间信号序列,从而实现时域信号到角域信号的转变,对重采样后的信号进行FFT变换,得到信号的阶次谱,并依据齿轮阶次和频率的关系,可以得出故障信号幅值与阶次的函数关系[9]。
在定量选矿废水中加入次氯酸钙粉末、次氯酸钠溶液、双氧水、高锰酸钾、氯酸钾等氧化剂各水体的COD浓度变化情况见表2。
1.2 小波阈值去噪
小波阈值去噪算法是一种对小波系数进行非线性处理的方法,通过设置一个适当的阈值,达到滤除噪声信号的目的。目前阈值的选取方式包括硬阈值法和软阈值法两种。其中硬阈值函数为
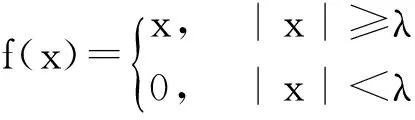
(6)
软阈值函数

(7)

2 风机增速箱故障信号重采样的实现及采样率的设置
重采样需要通过同步采集振动信号与参考轴的转速信号的方式实现,并通过对键相信号的计算和插值,实现对振动信号的等角度采样。计算键相脉冲到达时刻通常有两种方法:一种是在上升沿设定一个触发阈值;一种是在下降沿设定一个触发阈值。在定好触发阈值之后,至少选取靠近阈值的一点作为键相时标。其触发阈值的取值范围为
(8)
式中,fh为键相脉冲的高电平稳态值;fi为键相脉冲的低电平稳态值;fmax和fmin分别表示触发阈值的最大值和最小值。在其范围内选取一个触发阈值f,并设靠近触发阈值前后的两点分别记为fj和fj+1,与之对应的时间标记为tj和tj+1,采样的周期为T,则可利用两点线性插值法计算键相脉冲触发阈值处的时标ti为
(9)
由式(9)可得出触发阈值处的时标,由此可求得每段脉冲间隔的平均转速[11]
(10)
式中,k为每转的脉冲数。
由于重采样过程中角域信号受时域采样频率性质的影响以及采样后仍然需要经过FFT变换得到阶次谱,为了避免阶次混叠,在满足奈奎斯特采样定律的同时,角域采样的阶次应满足:
σs≥2 omax
(11)
式中,omax表示需要分析的最大阶次。即采样的角度间隔为
(12)
在对角域进行采样时,角域的采样率随转速的变化而变化,设某一时域信号X(ω,t)的采样率为fs,则依据采样定律,可得抗混滤波器的最大频率:
(13)
在角域可将此信号看作是随时域ω变化的变采样率采样信号,即
(14)
由式(11)~(13)可得与角域对应的时域抗混滤波最大阶次
(15)
(16)
综上所述,在时域内若想保留信息,依据式(16)及采样定理可得fs满足:
(17)
在角域采样时,若不进行抗混滤波,由式(10)、(15)可得
(18)
由式(17)、(18)可知重采样率是由时域采样频率和最小转速共同决定的,所以为了避免混叠现象,最终采样频率要比预设值大。
3 诊断实例分析
为了验证上述方法的优越性和可行性,对瓦房店某风场存在潜在故障的1.5MW风机(CCWE-1500/70.DF)增速箱进行了长时间的数据采集,在其增速箱的低速端和高速端安装加速度传感器,并采用Matlab软件对所测到的故障信号进行处理对比分析。其风机增速箱的结构简图如图1所示。

图1 增速箱的结构简图Fig.1 Structural diagram of gearbox
由图1可知,此型号的增速箱由一级行星轮系加二级平行轴组成。此次采集的振动信号以输入轴为参考轴,采样频率为2 048 Hz,采样时间5 s,依据主轴转速和各部件的啮合情况[12],可计算出二级齿轮额定工作状态下的1倍频、2倍频、3倍频分别为97.39 Hz、194.78 Hz、389.56 Hz,转动频率为9.8 Hz。此处齿轮点蚀的明显故障特征就是齿轮齿面磨损严重时会出现高阶振动,且随转轴频率的增大,振动能量也会明显增大。在增速箱的输出轴径向安装加速度传感器,其采集的故障振动信号的时域波形如图2所示。

图2 故障齿轮的原始信号Fig.2 Original signal of failure gear
由图2的时域信号可以看出,振动冲击比较明显,且信号中含有大量的噪声信号,由于转速的不平稳造成齿轮振动信号具有非平稳性,冲击的时间间隔也不均匀。对其先进行FFT分析,得到频谱图,如图3所示。

图3 故障齿轮振动信号的FFT频谱Fig.3 FFT spectrum of fault gear vibration signal
图3中该信号在275 Hz处波动,FFT谱是非常模糊的,无法有效判断其故障特征。本文分别利用经典计算阶次跟踪(COT)、阶次分析和小波阈值去噪相结合的方法对该故障信号进行处理分析。对原始信号进行sinc插值,得到等角度采样信号如图4所示,但由于得到的等角度采样信号同样会受噪声和调制的双重影响,使得阶次分析产生的分析效果不是太明显,所以对含有噪声信号的重采样信号选用db4小波对其进行分解,分解层数为5层,采用硬阈值方法去噪,所得的等角度采样信号如图5所示,可见去噪后的信号逼近程度高,无相位失真和信号损失,频谱更加清晰。

图4 等角度采样信号Fig.4 Angle sampling signal

图5 硬阈值去噪后的等角度采样信号Fig.5 The Angle sampling signal after the hard threshold de-noising
得到等角度采样信号后,对其分别进行FFT变换,得到了故障信号的阶次谱,如图6、7所示。
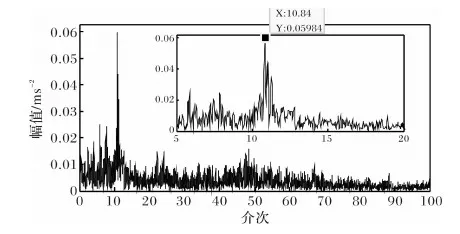
图6 基于COT重采样的阶次谱Fig.6 Order spectrum of re-sampling based on the COT

图7 硬阈值去噪后基于COT重采样的阶次谱Fig.7 Order spectrum of re-sampling based on the COT after the hard threshold de-noising

图8 故障信号阶次细化谱Fig.8 Zoom spectrum of fault signal order
由图4~7可以看出等角度重采样的信号比较稳定,得到的阶次谱与FFT谱相比较,消除了频谱的模糊现象。由图7可知,信号在10.84阶次处有明显的波峰,边频带少且稀疏,对应啮合频率的1倍频,故依据此处齿轮的故障特征初步定为磨损或点蚀。为进一步明确故障类型,将5~20阶次处的边频带局部细化,所得细化谱如图8所示,由细化谱可知,在啮合阶次10.84两端的变频较小,幅值的下降趋势比较明显,再结合时域波形的冲击振动比较明显来看,此故障应为点蚀故障。在本次的检修过程中,对风机齿轮箱进行了拆卸,发现风机齿轮箱内部太阳轮轴的齿轮齿面有金属块脱落的现象。此外为了验证阶次分析和小波阈值去噪相结合的方法与经典阶次跟踪方法(COT)重采样精度的差别,利用均方根误差来评价重采样精度。
(19)
由式(19)可以求出基于经典阶次跟踪方法重采样的均方根误差为0.9526,,基于小波阈值去噪和阶次分析相结合的方法重采样的均方根误差为0.3728,由此可知对信号进行经典阶次跟踪的重采样,再对其重采样后的信号进行小波阈值去噪,所得的重采样精度更高。
4 结论
大型风力机齿轮箱在实际运行过程中,由于受环境和自身结构的双重影响,对其所采集到的时域信号往往具有非平稳特性且含有大量的噪声信号,为了能更好的改善分析效果,提取故障信号的有效特征频率,本文将阶次分析和小波阈值去噪的诊断方法相结合,解决了因转速波动引起的频率模糊和阶次分析不适合在强噪声环境条件下工作的问题,并提高了重采样的精度,通过实践工程中的应用和理论上的对比分析,证明了此方法在处理旋转机械故障中的有效性,且能快速准确的诊断出风机齿轮箱的故障类型,在实际的故障诊断中具有广阔的工程前景和意义。
[1]JacekUrbanek,TomaszBarszcz,NaderSawalhi,etal.Comparisonofamplitude-basedandphase-basedmethodsforspeedtrackinginapplicationtowindturbines[J].MetrologyAndMeasurementSystems, 2011,XVIII(2): 295-304.
[2]BartelmusW. ,ZimrozR.Anewfeatureformonitoringtheconditionofgearboxesinnon-stationaryoperatingconditions[J].MechanicalSystemsandSignalProcessing, 2009, 23(5):1528-1534.
[3] 张磊,陈长征,刘杰.自适应EEMD法提取大型风机主轴承早期故障特征[J].重型机械,2015(3):5-8.
[4] 彭富强,于德介,武春燕.基于自适应时变滤波阶比跟踪的齿轮箱故障诊断[J].机械工程学报,2012,48(7):77-85.
[5] 陈向民,于德介,罗洁思.基于线调频小波路径追踪阶比循环平稳解调的齿轮故障诊断[J].机械工程学报,2012,48(3):95-101.
[6] 程军圣,李宝庆,杨宇.基于广义解调时频分析和瞬时频率计算的阶次谱方法在齿轮故障诊断中的应用[J].振动与冲击,2011,30(9):30-34.
[7] 丛华,吴广平,绕国强,等.计算阶次分析中避免阶次混叠的滤波定阶方法及其应用[J].振动与冲击,2012,31(12):42-45.
[8] 宋宝玉,解志杰,张锋,等.基于角度同步平均和阶次分析的低速斜齿轮故障诊断[J].吉林大学学报,2015,45(2):454-459.
[9] 岳晓峰,朱成伟.阶次分析在变速箱故障诊断中的应用及研究[J].自动化仪表,2015,36(6):8-11.
[10]景新幸,冼灿娇,杨海燕.基于改进小波阈值去噪算法的确定[J].电声技术,2015,39(5):80-83.
[11]李蓉,于德介,陈向民,等.基于阶次分析与循环平稳解调的齿轮箱复合故障诊断方法[J].中国机械工程,2013,24(10):1320-1326.
[12]Amirat Y, Choqueuse V, Benbouzid M.EEMD-based wind turbine bearing failure detection using the generator stator current homopolar component[J] Mechanical Systems and Signal Processing,2013,41(1):667-678.
Fault diagnosis of wind turbine gearbox based on order analysis
CHEN Chang-zheng, WANG Hai-tong, SUN Zi-qiang
(School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110178, China)
Wind turbine run under the poor working conditions, vibration signals often have the character of non-stationary. In order to extract the characteristic frequency of fault information, a new diagnosis algorithm is proposed based on the re-sampling order analysis and wavelet threshold de-noising. Compared with the algorithm of classical calculation order tracking (COT), the accuracy of re-sampling is improved, and compared with the methods of traditional FFT to eliminate the phenomenon of “frequency aliasing” cased by speed instability. Then through the wind field experiment shows that the method is effective and valuable in engineering.
wind turbines; wavelet de-noising; order analysis; re-sampling
2015-08-21;
2015-09-25
辽宁省自然科学基金(2014028017)
陈长征(1964),男,辽宁省沈阳市,教授,博士生导师,主要从事振动噪声的研究。
王海童(1988-),男,沈阳工业大学硕士研究生。
TH132.46
A
1001-196X(2016)02-0086-05

