沪深300股指期货交易量与波动率关系的分析

鹿 波

（北京金融衍生品研究院有限责任公司，北京100033）

技术分析有两种类型，一种是单纯根据资产价格对未来进行预测，一种是根据资产价格和交易量两方面的数据对未来进行预测。交易量中是否包含关于资产价格的信息是一个值得研究的问题，学术界对量价关系的研究也非常多。当前我国股指期货在实施临时性管制措施之后，交易量急剧减少，管制措施前后市场中量价关系是否发生了显著变化，如果发生变化，这种变化有什么含义？

一、文献回顾

关于收益率、波动率与交易量的关系的研究有很多，实证研究发现很多金融市场的波动率与交易量存在同期正相关关系，股票市场上存在正相关关系的还有收益率与交易量。Karpoff（1987）对之前量价关系方面的学术研究进行了总结，关于波动率与交易量的同期正相关关系，有以下几个理论解释：序列信息到达假说 （Sequential arrival of information）、混合分布假说（Mixture of distribution hypothesis，MDH）、生命周期交易假说 （life-cycle trading），关于股票市场上收益率与交易的同期正相关关系的解释较为一致，即来自于卖空交易的限制。这之后有文献从投资者信念和行为金融的角度对金融市场上的量价关系进行研究。Harris和Raviv（1993）构建的模型表明投资者对于相同信息的不同理解也能够解释价格波动与交易量之间的正相关关系。Shalen（1993）构建的两期期货市场理性预期模型表明对未来价格的不同预期有助于解释价格波动与交易量之间的正相关关系以及绝对价格变化序列的正相关特征。Statman，Thorley和Vorkink（2006）发现市场收益率对之后数月甚至数年的市场和个股的交易量有正的影响，并将这一现象归因于投资者的过度自信。此外，MDH模型也有所发展，Andersen（1996）假设收益率和交易量都受到信息到达频率Kt的影响，并使用修正之后的MDH模型和广义矩估计方法对真实数据进行校准，发现解释力优于标准MDH模型。Hasrouck（1991a）和（1991b）使用VAR模型分析不同股票的交易量与价格变动之间的关系，假设价格对交易不具有同期影响，而交易对价格具有同期影响，因此交易量方程残差可以看做是私人信息，而价格方程的残差可以看做是公共信息，通过脉冲响应函数分析，可以得到不同股票的私人信息占比，结果发现股票市值越大，私人信息占比越小，信息不对称程度越小。期货市场上量价关系的研究也有很多。Daigler和Wiley（1999）使用两变量GARCH模型研究期货市场波动率和交易量的关系，其中交易量数据根据投资者类型进行进一步划分，发现波动率和交易量之间的关系因投资者类型的不同而不同。国内的研究，张永冀、汪昌云和华晨（2013）使用VAR和SVAR模型发现历史量价关系信息在中国股票市场价格发现中比单纯历史价格信息更有效。

二、实证分析

（一）划分不同的考察区间

本文使用沪深300股指期货品种主力合约2010年4月16日至2016年5月5日的日度、周度和月度收益率和交易量数据，收益率采用对结算价取自然对数并差分的方法计算。平稳性检验表明，收益率序列是平稳的，而交易量数据在全区间内是不平稳的。进一步划分为2015年9月前后两个区间，分别进行平稳性检验，发现2015年9月之前仍然是趋势平稳序列（表1）。为了将交易量数据变为平稳，需要进行去趋势操作。时间序列去趋势的方法有很多种，既有参数方法，也有非参数方法。各种方法选择的主观性较大，因此，我们不采用去趋势的方法，而是进一步划分时间区间以求在更短的区间内消除交易量数据的时间趋势。

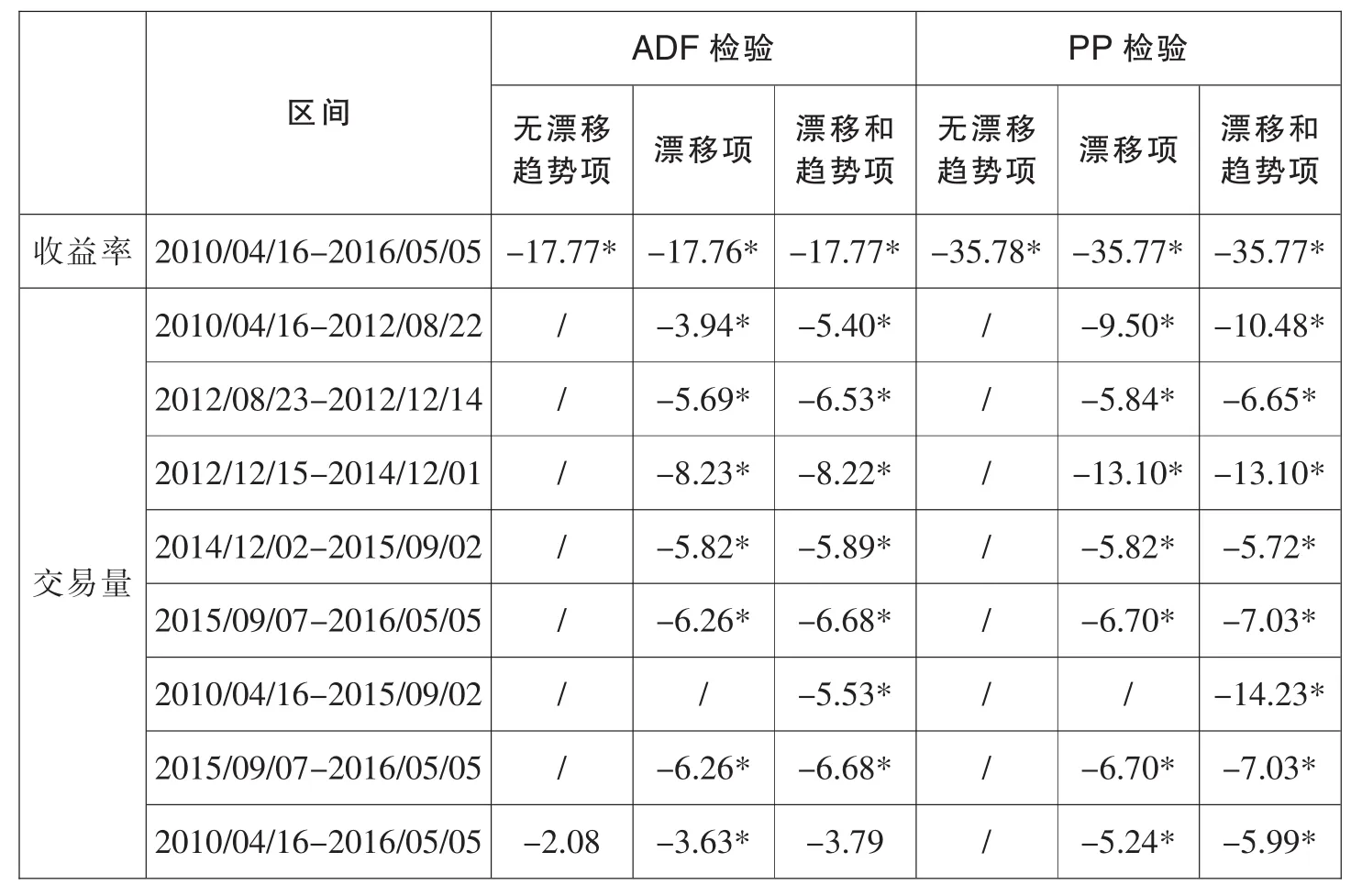
表1 沪深300股指期货收益率和交易量数据的单位根检验统计量①

划分区间的方法参考Inclan和Tiao（1994），简单来说就是寻找成交量的分布发生变化的断点，然后根据这些断点将整个样本区间划分成多个子区间，使得每一个子区间内成交量都保持相对的稳定。最终沪深300股指期货的子区间如图1所示，具体划分方法参见附件1。子区间内交易量数据都是平稳的（表 1）。

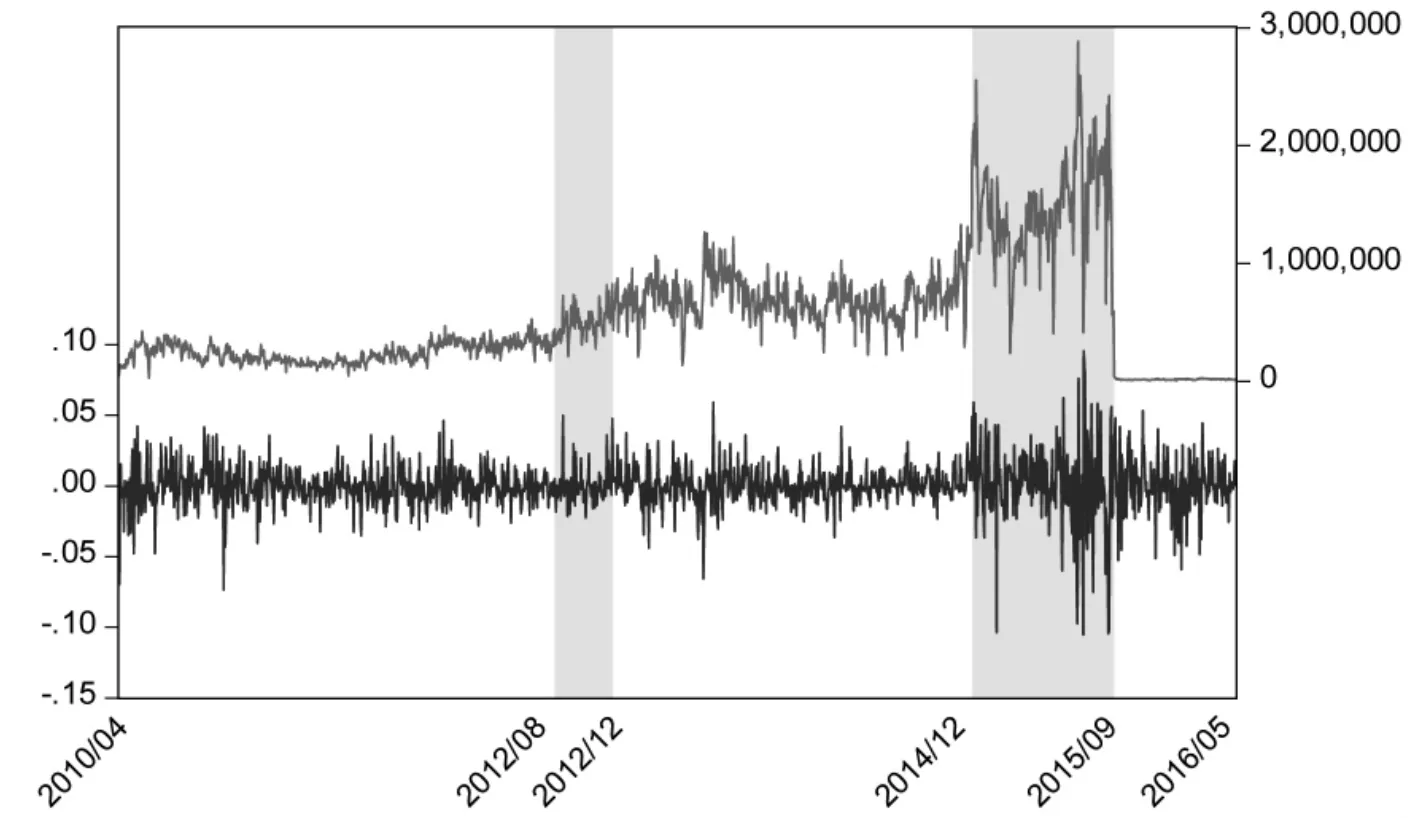
图1 沪深300股指期货按照成交量划分的五个子区间②

（二）同期相关性分析

下面分析交易量与收益率和波动率的同期相关性。学术研究发现从长期来看，收益率与交易量的同期相关性与做空成本有关系，做空成本越高，两者的正相关性越高。因为做空成本越高，市场下跌时相比于市场上涨时的交易量越少，市场表现出“量价齐升”和“量价齐跌”的可能性越大。因此，从理论上来说，期货市场的收益率与交易量不会存在相关关系。而不同的学术研究发现，波动率与交易量的同期相关性则与信息到达的频率、信息传播的速度、投资者的信念差异等多种因素有关。本文中波动率采用两种代表方式，一种是收益率的平方（R 2），一种是GK估计量，即使用Garman和Klass（1980）的计算公式：

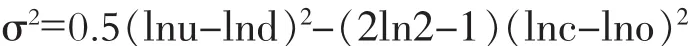
其中lnu、lnd、lnc和lno分别代表取自然对数之后的最高价、最低价、收盘价和开盘价。GK估计量更多地考虑了期内价格的变化。根据Garman和Klass（1980），GK估计量相比R2的效率提高7倍。

表2给出了同期相关性的实证结果。除区间二之外，收益率与交易量的相关性较弱。因此从实证上来说，收益率和交易量长期来看不存在同期相关关系。以GK估计量代表的波动率与交易量的同期相关性在所有区间均为正值，且日度数据得到的相关性均显著为正。另外，GK估计量与交易量的相关性在绝大多数情况下均大于R2与交易量的相关性。

表2 股指期货不同区间收益率和波动率与交易量的同期相关系数④

（三）SVAR 分析

1.日度数据分析

下面使用SVAR模型对收益率、波动率和交易量，特别是波动率与交易量之间的相互关系进行分析。SVAR模型考虑了收益率、波动率和交易量三者之间的同期相关关系，因此比VAR更合理。假设收益率对波动率不具有同期影响，收益率和波动率对交易量不具有同期影响。在此假设之下，由Hasbrouck（1991a）和Hasbrouck（1991b），交易量方程的残差代表未预期交易产生的信息，包括私人信息和公共信息发布之后通过交易在市场中传播的信息，但更多的是私人信息；波动率方程的残差代表剔除交易产生信息之后的其他信息，包括公共信息和由于市场机制（例如价格变动的非连续）方面的原因产生的价格变动，但更多的是公共信息。此外，由于三个变量之间的量纲差别巨大，为了减少计算误差，需要对变量进行调整。我们在五个区间内分别对收益率、波动率和交易量数据进行减均值除以标准差的标准化变换，然后使用变换之后的数值进行SVAR分析。各区间滞后阶数取AIC准则确定的所有最优滞后阶数的最大阶数，即6阶。交易量和波动率之间的同期相互关系如表3所示。除区间四之外，交易量对日度以R2代表的波动率（日间波动率）均具有显著的正影响；所有区间内的交易量对以GK估计量代表的波动率（日内波动率）具有显著的正影响。

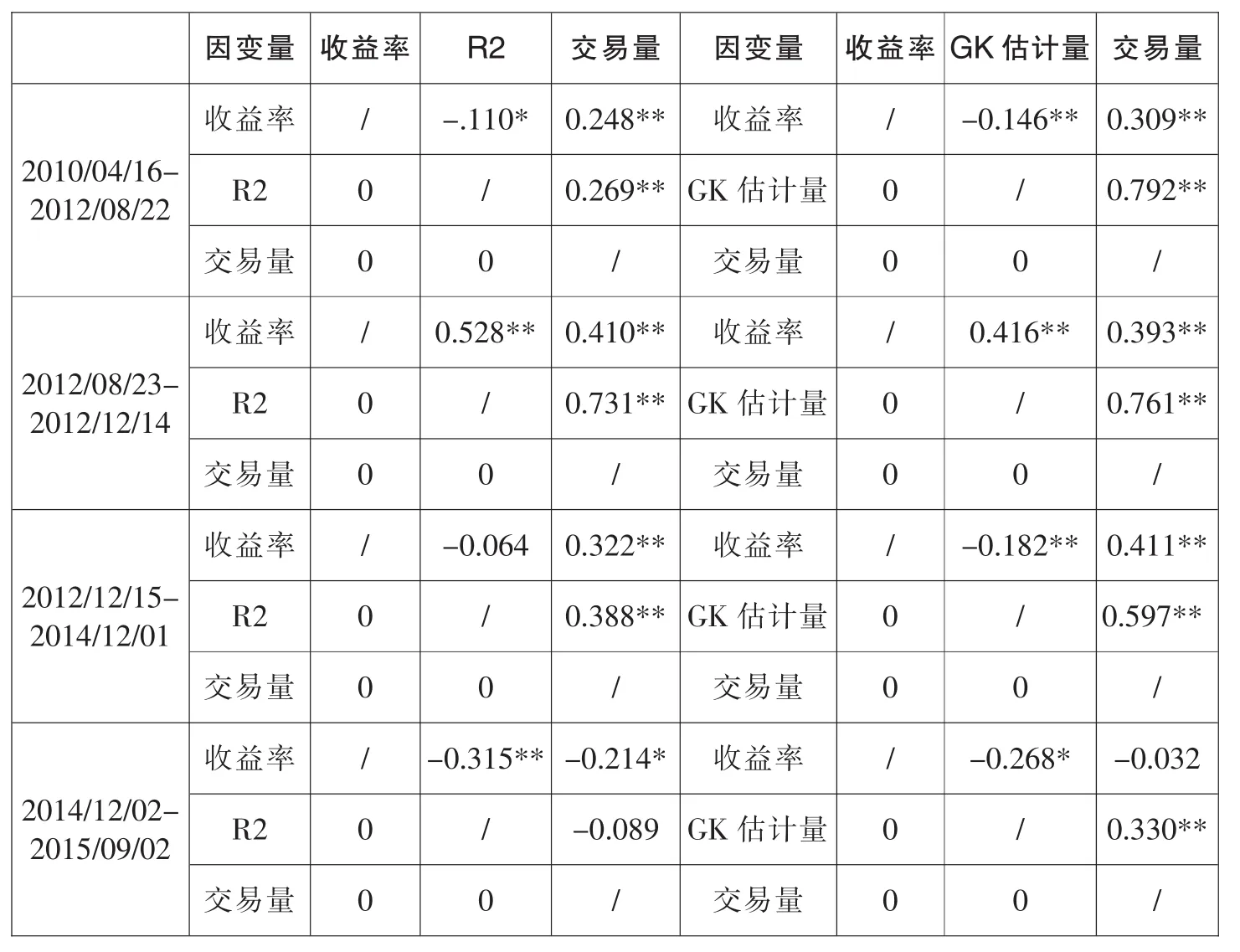
表3 SVAR分析中收益率、波动率与交易量的同期相互关系⑤

2015/09/07-2016/05/05收益率 / -0.176 0.231 收益率 / -0.354* 0.313*R2 0 / 0.365**GK估计量 0 / 0.459**交易量 0 0 / 交易量 0 0 /

下面依据SVAR模型进行结构脉冲响应分析，结果如表4所示，数值代表自变量一个标准差的变动所引起的因变量数值的变化，由于数据都进行了标准化，因此也代表自变量一个单位变动引起因变量的变动。交易量（私人信息）对波动率的影响方面，区间四的交易量对日间波动率不具有显著影响，除此之外交易量对日间波动率和日内波动率均具有显著正影响。波动率（公共信息）对交易量的影响方面，区间四的日间波动率对交易量具有显著的正影响，除此之外波动率对交易量影响不显著。

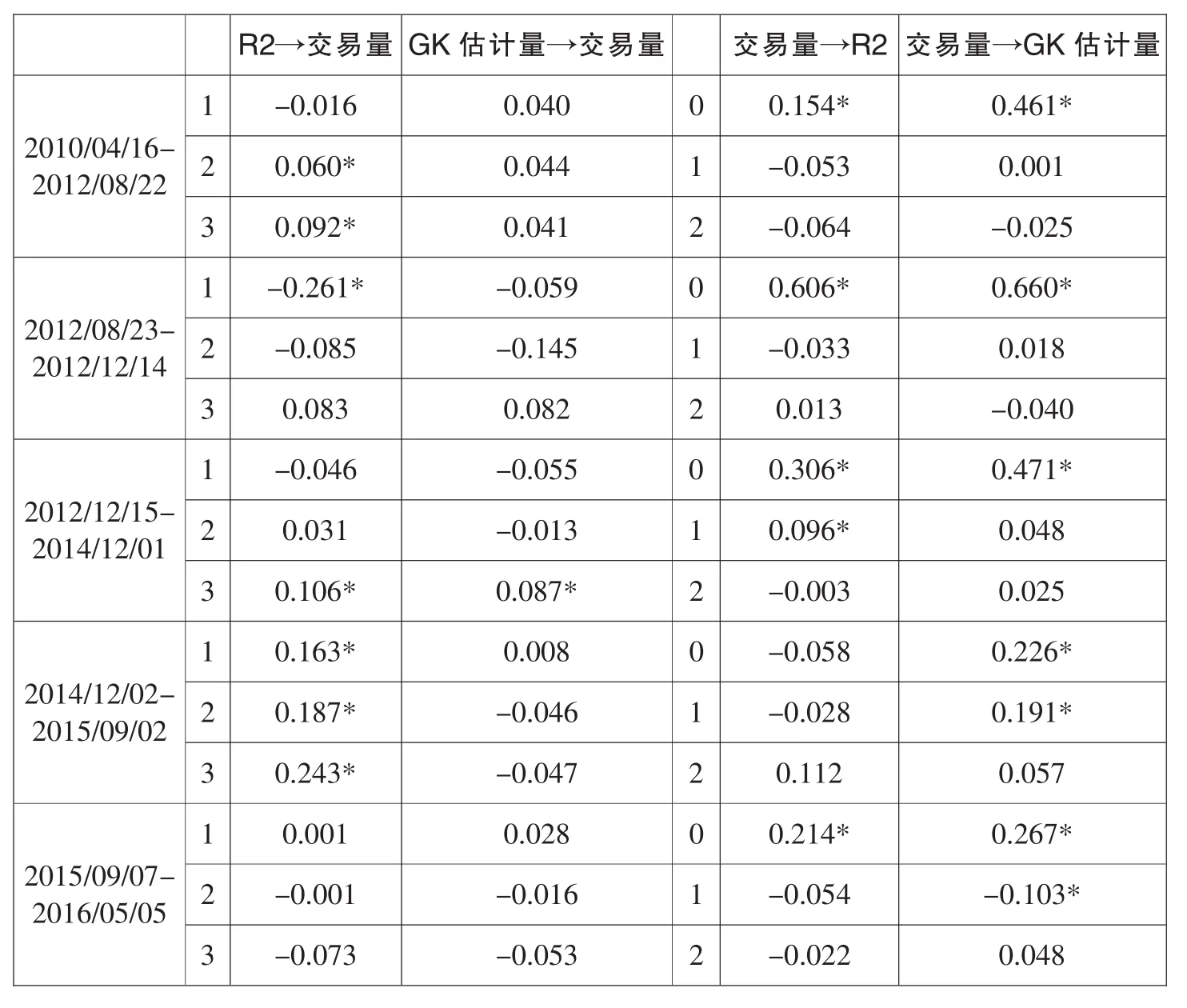
表4 波动率与交易量的结构脉冲响应分析

2.稳健性检验

（1）滞后阶数

将SVAR模型的滞后阶数调整为2期和4期，得到的结构脉冲响应结果如表5所示。滞后2阶和4阶的结果与滞后6阶一致。区间四的日间波动率对交易量具有显著正影响，交易量对日间波动率则不具有显著影响。波动率对交易量的持续影响意味着波动率越大，接下来几天交易越多，这些增加的交易都是跟风交易，跟风交易又会对日内波动率产生影响。因此，区间四波动率的增加与跟风交易增多有一定关系。区间五的日内波动率受交易量的影响存在过度反应，根据序列信息到达假说理论，这表明采取限制措施之后，市场深度变差，私人信息通过交易扩散到市场中的进程拉长。除此之外，交易量对波动率均具有显著的正影响，波动率对交易量不具有显著影响。

表5 波动率与交易量的结构脉冲响应分析（滞后2期和4期）

（2）量纲

假设数据不做标准化变换，而是适当调整量纲，收益率使用乘以100之后的数值，波动率使用乘以10000之后的数值，而区间一至区间四的日度交易量数据使用除以100000之后的数值，区间五的日度交易量则使用除以1000之后的数值，则结构脉冲响应分析的结果如表6所示，结果与标准化变换一致。

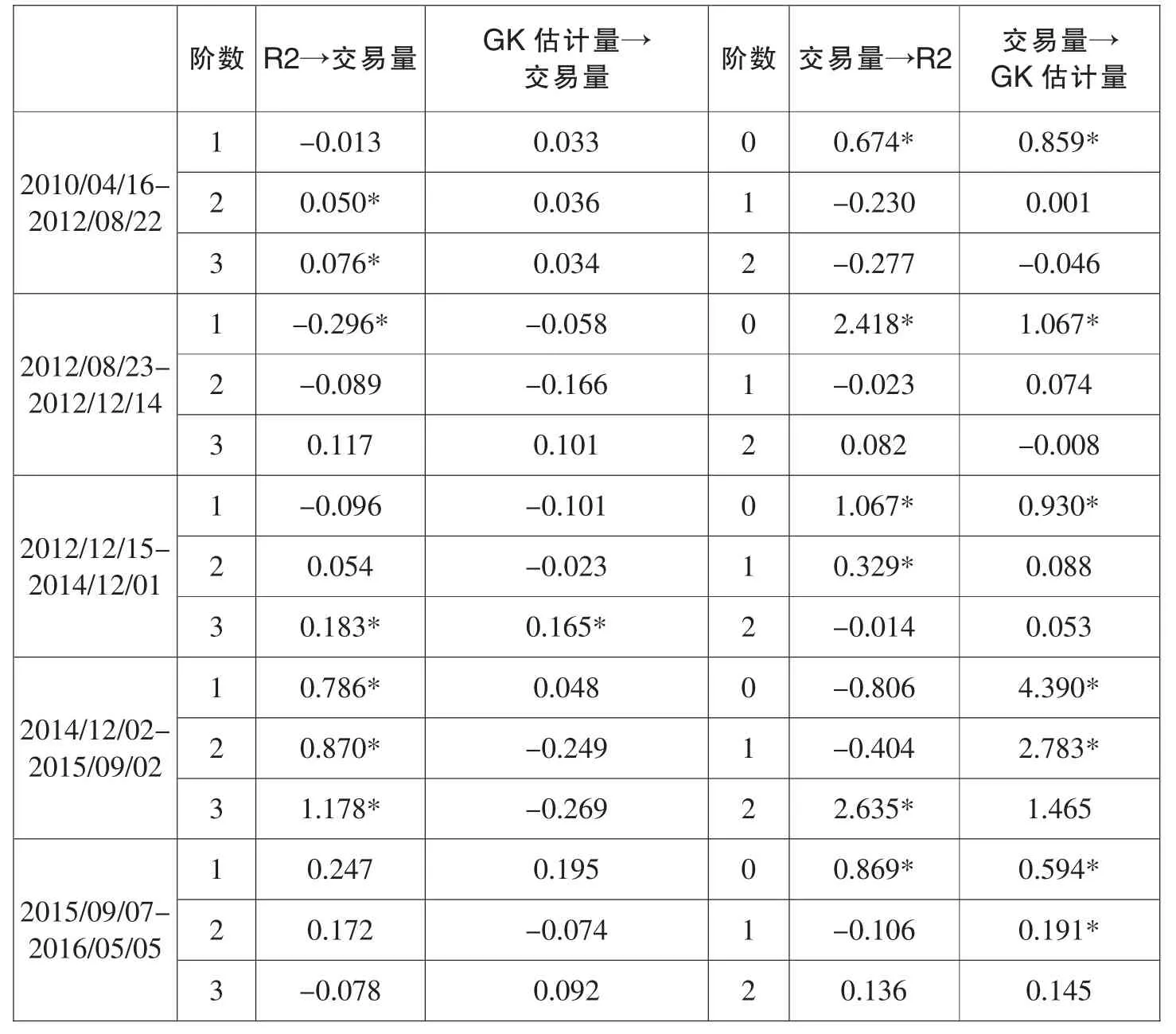
表6 波动率与交易量的结构脉冲响应分析（量纲调整）

3.周度数据分析

使用标准化变换之后的周度数据进行SVAR分析，得到的结果如表7所示。区间一的周间波动率对交易量具有显著正影响，交易量对周间波动率则没有显著影响，表明区间一内也存在一定的跟风交易。除此之外波动率对交易量没有显著影响，由于周度的波动率数据受市场机制的影响比日度数据小，因此周度波动率方程的残差更能够代表公共信息，上述结果表明公共信息对交易量没有显著影响。交易量对周内波动率的影响在绝大多数情况下显著为正，只是在区间四内同期影响不显著，交易量对周间波动率的同期影响也均为正，只是在区间一和区间五不显著，表明区间五交易的信息含量减少。值得一提的是，周度数据在区间二、区间四和区间五内的样本个数较少，在区间二内甚至只有14个样本点，因此统计结论的稳健性可能受此影响。

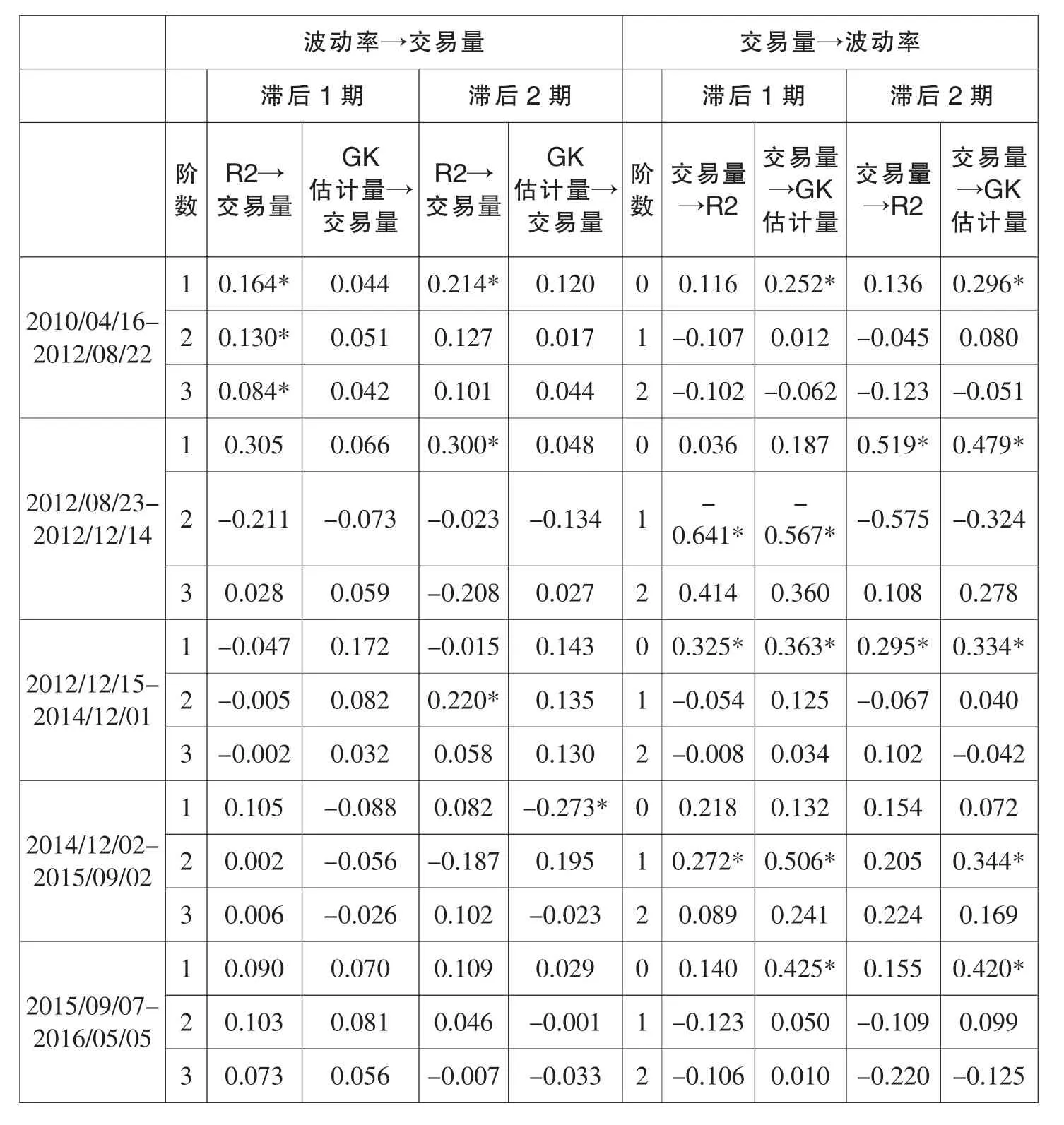
表7 波动率与交易量的结构脉冲响应分析（周度数据）

（四）私人信息占比

根据 Hasbrouck（1991a）和 Hasbrouck（1991b），在脉冲响应分析中，假设交易量冲击（私人信息）对波动率的累积影响为a*，波动率受自身滞后期冲击（公共信息）的累积影响为b*，则私人信息在所有信息中的占比可以表示为：

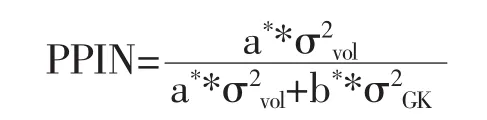
其中，σ2vol代表交易量方程中残差的方差，σ2GK代表波动率方程中残差的方差。五个区间相应数值如表8所示，区间五由于股指期货交易所带来的私人信息在所有信息中的占比明显低于其他区间，因此区间五股指期货交易的信息含量有所降低。

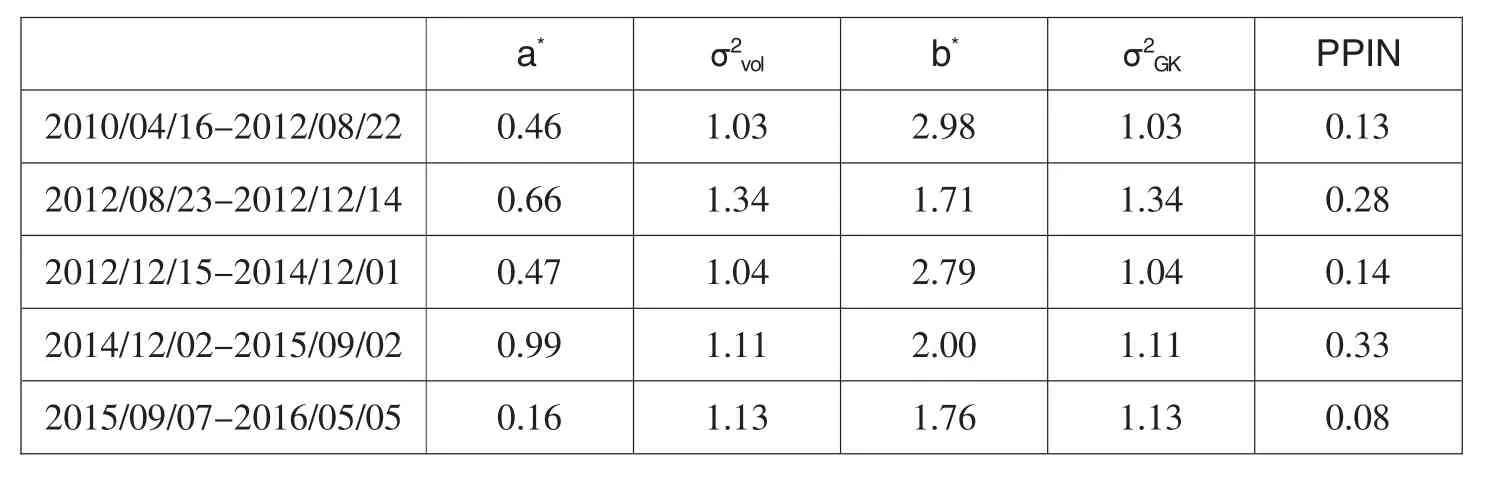
表8 私人信息在所有信息中的占比

三、结 论

通过上述分析，可以发现波动率冲击（公共信息）对交易量的影响在多数情况下不显著，而交易量冲击（私人信息）对波动率的影响在多数情况下显著为正。这表明在多数情况下股指期货交易含有显著的私人信息成分，而且跟风交易并不显著。股市波动较大时，股指期货交易存在一定的跟风交易成分。管制措施实施之后，市场深度变差，私人信息通过交易扩散到市场中时存在过度反应，信息传播过程拉长，且私人交易在所有信息中的占比下降。因此，应当尽快解除股指期货的临时管制措施，促进股指期货的功能发挥。

附件1

划分股指期货不同区间的方法介绍

我们参考了Inclan和Tiao（1994）的方法，并对此方法进行了改进。

1.统计量

根据Inclan和Tiao（1994），如果变量M服从卡方分布，则有关于M的统计量：其中，T是拟考察的时间区间，K=1,2,3……T。假设卡方分布的自由度在T内不发生变化，则统计量DK渐进服从布朗桥（Brownian bridge）过程。根据显著性水平P的不同，存在不同的渐进分布临界值。如果在k=处超过临界值，则表明原假设不成立，M服从卡方分布的自由度在前后发生了变化。

2.临界值

根据Inclan和Tiao（1994）的结论，样本数量大于200时，渐进临界值就会比较有效，因此我们使用渐进临界值。我们使用1%显著程度下的临界值1.628对交易量数据进行区间划分。

3.检验过程

与Inclan和Tiao（1994）不同的是，本文使用改良之后的检测程序。Inclan和Tiao（1994）首先对全区间进行检测，如果不存在大于临界值的点则检测结束，全区间没有变化点。如果存在变化点，假设第一个变化点是t1，最后一个变化点是tn，则分别在[0,t1][tn,T]两个区间内分别进行检测，如果两个区间内都没有大于临界值的点，则t1就是全区间的第一个变化点，tn是全区间的最后一个变化点。然后，继续在[t1,tn]区间内进行上述步骤，直到每一个子区间内都没有大于临界值的点为止。该程序不便于编程操作，因此我们对检测程序进行了改良。首先对[0,2]进行检测，如果不存在大于临界值的点，则对[0,3]进行检测，直到发现[0,n]内存在大于临界值的点，这时[0,n-1]就是第一个无变化点的区间，接着对[n,n+2]进行检测，如果不存在大于临界值的点，则对[n,n+3]进行检测，以此类推。

4.考察变量

划分样本区间的考察变量M是成交量。成交量服从伽马分布，而卡方分布是一种特殊的伽马分布，因此，成交量近似满足卡方分布的假设条件。

注释：

① 采用日度数据，*代表在1%显著水平下拒绝存在单位根的原假设，未标出的区域表明前一步骤拒绝零假设且趋势项和漂移项显著，趋势项和漂移项的临界值参考张晓峒和攸频（2006）。

②图中上方曲线代表成交量，下方是收益率，白色和灰色区域间隔代表五个子区间。

③公共信息指市场上所有参与者都可以获得的信息，包括宏观经济政策、市场监管措施等。

④*代表1%显著水平下显著，区间二的月度数据样本数为8，统计量受样本影响较大，因此未给出相关系数。

⑤ *代表1%显著水平下显著，假设交易量与收益率同期不相关。

[1]Andersen T G.Return volatility and trading volume： An information flow interpretation of stochastic volatility[J].The Journal of Finance，1996，51（1）： 169-204.

[2]Daigler R T，Wiley M K.The impact of trader type on the futures volatility‐volume relation[J].The Journal of Finance，1999，54（6）： 2297-2316.

[3]Harris M，Raviv A.Differences of opinion make a horse race [J].Review of Financial studies，1993，6（3）： 473-506.

[4]Hasbrouck J.Measuring the information content of stock trades [J].The Journal of Finance，1991，46（1）： 179-207.

[5]Hasbrouck J.The summary informativeness of stock trades： An econometric analysis[J].Review of Financial Studies，1991，4（3）： 571-595.

[6]Inclan C，Tiao G C.Use of cumulative sums of squares for retrospective detection of changes of variance[J].Journal of the American Statistical Association，1994，89（427）： 913-923.

[7]Karpoff J M.The relation between price changes and trading volume： A survey [J].Journal of Financial and quantitative Analysis，1987，22（01）： 109-126.

[8]Shalen C T.Volume，volatility，and the dispersion of beliefs [J].Review of Financial Studies，1993，6（2）： 405-434.

[9]Statman M，Thorley S，Vorkink K.Investor overconfidence and trading volume [J].Review of Financial Studies，2006，19（4）： 1531-1565.

[10]张永冀，汪昌云，华晨.历史价量信息在价格发现中更有效吗?——基于中国证券市场的数据分析[C]//中国管理科学学术年会.2013.