基于稀疏表示分步重构算法的高光谱目标检测
廖佳俊,刘志刚,姜江军,路志勇
基于稀疏表示分步重构算法的高光谱目标检测
廖佳俊1,刘志刚1,姜江军1,路志勇2
(1. 火箭军工程大学,陕西 西安 710025;2. 96831 部队,北京 100015)
针对传统稀疏表示重构算法在高光谱目标检测中表现出运算速度慢的问题,提出了分步重构算法(Two Steps Reconstruction,TSR)。该方法先求得个与待测像元最相似的字典原子,然后用这些原子线性表示待测像元以求解稀疏向量,舍弃了传统重构算法的迭代求解的方式,直接通过求解逆矩阵,简化了运算过程,使运算速度大幅提高。本文给出了方法的具体过程并将其与传统方法及其改进方法进行比较。实验结果表明,TSR在保证检测精度不下降的同时能够大幅提升运算速度。
高光谱目标检测;重构算法;稀疏表示
0 引言
目标检测是高光谱遥感技术应用的重要方向之一,它涵盖了环境监测、城市调查、矿物填图和军事侦察等诸多领域。传统的目标检测方法有光谱角填图(Spectral Angle Mapping,SAM)、匹配子空间(Matched Subspace Detector,MSD)、正交子空间投影(Orthogonal Subspace Projection,OSP)等[1]。这些方法在高光谱目标检测方面有着广泛的运用,但也存在检测结果精度不高、对分布模型假设准确与否关系大等不足之处。今年来,稀疏表示理论在图像处理及目标检测中取得了较好的发展[2-3]。2010年,Yi Chen等人将稀疏表示成功应用于高光谱图像分类和目标检测[4-5],取得了不错的效果。越来越多的学者开始关注将稀疏表示应用于高光谱图像,稀疏表示为高光谱目标检测提供了一条新的研究思路。基于稀疏表示的方法虽然能克服传统方法精度不高以及需要假设分布模型等问题,但由于高光谱图像光谱分辨率高带来的海量数据,使得目前稀疏表示中应用比较广泛的正交匹配追踪算法(Orthogonal matching pursuit,OMP)[6]在计算时由于迭代次数过多而造成运算量大、速度慢的问题,特别是当字典中原子数目过多或者稀疏度过高时会使得计算复杂度成指数增长。在压缩感知领域,不少学者提出了许多OMP算法的改进形式,包括gOMP、StOMP、SWOMP和CoSaMP[7-10]等;赵春晖等人将StOMP算法应用到高光谱目标检测之中,取得了一定的效果[11]。我们将上述改进方法应用在高光谱目标检测中发现,由于光谱的复杂性使得高光谱待测像元并不能由字典中的原子精确重构,有些算法在运行时可能并不是由重构误差达到精度而完成重构而是由于达到迭代次数而完成重构,所以目标检测效果并不理想。针对这个问题,本文提出了一种分步重构算法,放弃了原来迭代求解的思路,而通过直接求解逆矩阵实现重构,使运算速度得到大幅提高。
1 基于稀疏表示的高光谱目标检测及OMP算法概述
稀疏表示的思想就是将原始信号表示为字典与稀疏向量相乘的形式:
=(1)
式中:是一个过完备字典;稀疏向量是一个只有少数元素不为零的向量。
在高光谱目标检测中,一个待测像元可以通过大量端元中部分原子的线性组合表示。对应于稀疏表示,可将大量端元构成一个超完备字典,由目标子字典t和背景子字典b级联构成,那么待测像元可以由下式表示:

式中:t和b分别对应目标子字典t和背景子字典b的稀疏向量。通过求解稀疏向量并判断t和b是零向量还是稀疏向量即可判断该待测像元是目标还是背景。算法基本原理如图1所示。
该方法关键性步骤之一就是求解稀疏向量的重构算法,其中最为常见的就是OMP。其主要思路可以简单总结如下:
Step 1:初始化残差0=,索引矩阵0=Æ,字典支撑集0=Æ,迭代次数=1。

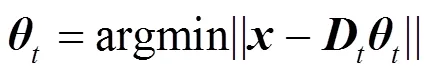
Step 4:更新残差r=-。

2 分步重构算法
重构算法的目标是找到个合适的字典原子以表示待测像元。OMP算法采用逐个求解的思路,由于反复迭代,运算时间很长。为了提高效率,可否一次性求解个合适的字典原子呢?根据这一思路,本文提出了一种分步重构的算法,舍弃了迭代求解的方式,试图使运算过程得以简化。该方法流程图如图2所示,具体步骤如下:
第一步:从字典中选取个与待测像元最相似的原子。
在这一步中本文提出两种求解方法:线性表示法和直接表示法。相对而言,线性表示法在像素点多,稀疏度高的情况下速度更快;直接表示法在稀疏度稍低的情况下速度更快。其方法具体原理如下:
1)线性表示法(Two Steps Reconstruct with Linear Representation,TSR-L)
假设待测像元可以表示为如下等式:
=11+…+da=(3)
式中:表示待测像元;1, …,d表示字典中的各个原子;1, …,a表示系数。
由于通常是奇异矩阵,可以通过式(4)求解:
=(D+I)-1x(4)
式中:是一个极小的正则化项;是单位矩阵。
通过式(3)可以发现每一个原子都对待测像元的表示都做出了贡献。计算每一个原子与待测像元的残差:

其中ei可以表示每一个字典原子与待测像元之间的差别,较小的ei对应字典原子对待测像元贡献度越大。那么通过比较ei就能够确定K个与待测像元最相似的字典原子,记为d1,…,dK,该方法通过逆矩阵一次求出每个原子对应的贡献度,对于稀疏度越高的情况效果越明显。
Fig.1 Basic principle of Sparse representation

图2 算法流程图
Fig.2 Flow chart of algorithm
2)直接表示法(Two Steps Reconstruct with Direct Representation TSR-D)
第一步主要问题是求出个与待测像元相似的字典原子,由于待测信号与字典原子都进行了归一化处理,假设字典原子与待测像元的相似度可由下式表示:
L=xd,=1, …,(6)
式中:L越大表示相似度越高,通过排序后,取出前个值,即可求得与待测像元最相似的个字典原子,记为1,…,d,该方法由于计算简单,在大多数情况下效果突出。如果待测像元是目标像元,那么1,…,d中全部或者大部分都应该属于目标子字典,否则应全部或大部分属于背景子字典。
第二步:用选出的个字典原子的线性组合进一步表示待测像元,计算稀疏向量。
假设待测像元满足如下等式:
=11+…+bd=bD(7)
式中:1,…,d表示与待测像元最相似的字典原子;1,…,b表示系数。由于通常也是奇异矩阵,那么可以通过式(7)求解:

式中:是一个极小的正则化项;是单位矩阵。
然后,将中原子和根据式(8)求出来的对应的系数的乘积之和分别求目标和背景的重构误差t和b,如式(9)所示:

式中:t表示目标子字典原子及其对应系数相乘之和;b表示背景子字典原子及其对应系数相乘之和;若待测像元为目标,那么t应当越小,b应当越大,反之亦然。最后设置一个阈值,通过求t和b的差值(),如式(10)所示:

根据上述步骤,即可实现对高光谱图像的目标检测处理。可以看出,本方法舍弃了迭代求解稀疏向量的形式,通过直接求逆矩阵的形式求解稀疏向量,简化了运算。
3 实验结果及分析
在本章中,采用3组实测高光谱图像数据对本文提出的算法进行验证,以接收机特性(Receiver Operating Characteristic,ROC)曲线下的面积(Area Under the Curve,AUC)[12]为检测结果的效果指标,将检测效果和时间与OMP、StOMP、gOMP算法进行对比。本文字典的选取采用文献[3]提出的方法,其中目标子字典原子个数依次分别为52,38,38;背景子字典窗口大小为内窗7×7,外窗11×11,共计72个原子;稀疏度=16。实验环境为Dell Precision T1650图形工作站;8核处理器,主频3.30GHz;内存16G;操作系统:Microsoft Windows7;程序运行平台:MATLAB 2014a。
3.1 MSHyperSIS水杯数据
第一组实验数据是用地面MSHyperSIS成像光谱仪获取的一幅高光谱图像。图像原始大小为260×336,共256个波段。本实验中所用的图像数据是从原始图像中裁取出来的,其大小为80×80,剔除其中的无效波段,保留有效波段181个。实验数据如图3所示,图像区域为一片水泥地,水泥地中放置了一个水杯为待检测的目标。其中,图3(a)是第69个波段的灰度图,图3(b)是水杯的空间分布图。

图3 实验数据图像
Fig.3 Experimental image
图4(a)~(e)给出了OMP、StOMP、gOMP、TSR-L、TSR-D的目标检测效果图。其目标检测所对应的AUC值以及所消耗的时间如表1所示。

图4 图3的检测结果对比

表1 图3用不同重构方法所得AUC值及时间
从图4和表1中可以看出各种算法检测结果相差不大,OMP算法运算速度相对较慢;基于OMP算法改进的StOMP算法速度有所提升,但检测精度略有下降;gOMP算法运算速度不升反降;本文提出的分步重构算法对比于OMP算法在检测精度略有提高的情况下,TSR-D运算速度大幅提升,降低到OMP的15.2%,而TSR-L运算时间则略有增加。
3.2 AVIRIS数据
第2组数据为机载可见光及红外成像光谱仪(Airborne Visible/Infrared Imaging Spectrometer, AVIRIS)拍摄的美国圣地亚哥海军机场的高光谱图像。该高光谱图像波长范围为370~2500nm,空间分辨率为3.5m,大小为400×400个像元。截取其中100×100的子图像,除去水汽吸收波段和信噪比较低的波段后,保留189个波段。图5(a)是第204波段的灰度图,图5(b)是停靠飞机的空间分布图。
图6(a)~(e)给出了OMP、StOMP、gOMP、TSR-L、TSR-D的目标检测效果图。其目标检测所对应的ROC曲线下面积值以及所消耗的时间如表2所示。

图5 实验数据图像
从图6和表2中可以看出OMP算法运算速度相对较慢;基于OMP算法改进的StOMP算法速度有所提升,检测精度略有下降;gOMP算法运算速度不升反降;本文提出的分步重构算法对比于OMP算法在检测精度略有提高的情况下,运算速度大幅提升,其中TSR-L运算时间降低到OMP的64.2%,TSR-D降低到OMP的29.3%。

图6 图5的检测结果对比
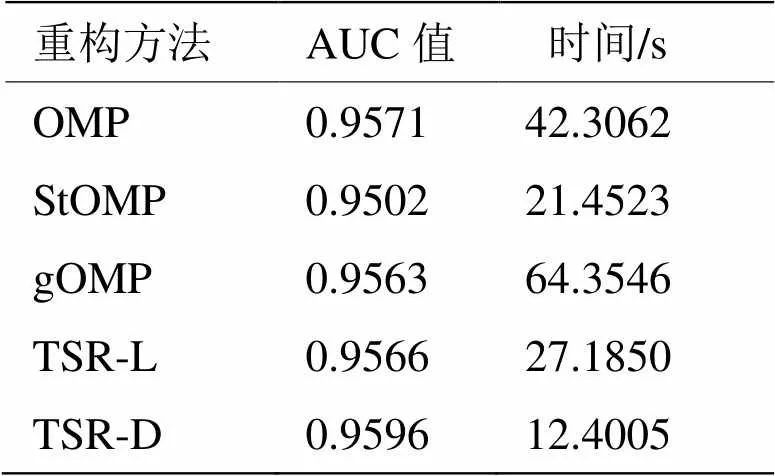
表2 图5用不同重构方法所得AUC值及时间
3.3 MSHyperSIS迷彩服数据
第3组实验数据是用地面MSHyperSIS成像光谱仪获取的一片以树林为背景的高光谱图像。图像原始大小为500×336,共256个波段。本实验中所用的图像数据是从原始图像中裁取出来的,其大小为200×200,剔除其中的无效波段,保留有效波段181个。实验数据如图7所示,图像区域为一片树林,树林中放置的3件迷彩服为待检测的目标。其中,图7(a)是第69波段的灰度图,图7(b)是迷彩服的空间分布图。

图7 实验数据图像
图8(a)~(e)给出了OMP、StOMP、gOMP、TSR-L、TSR-D的目标检测效果图。其目标检测所对应的ROC曲线下面积值以及所消耗的时间如表3所示。

图8 图7的检测结果对比

表3 图7用不同重构方法所得AUC值及时间
从图8和表3中可以看出OMP算法运算速度也相对较慢;基于OMP算法改进的StOMP算法速度有所提升,检测精度略有下降;gOMP算法运算速度不升反降;本文提出的分步重构算法对比于OMP算法在检测精度略有提高的情况下,运算速度大幅提升,其中TSR-L运算时间降低到OMP的62.5%,TSR-D降低OMP的28.9%。
3.4 实验结果分析
对比上述3组实验结果可以看到,StOMP算法相比于OMP算法在运算速度上有一定的提升,但精度有少许降低,这可能是因为每次迭代选择多个原子不如选择单个原子精确度高。gOMP算法在运算速度上不升反降,这可能是因为运行时不是由重构误差达到精度而完成重构而是由于达到迭代次数而完成重构。TSR-D在所有数据中均有最好的表现,不仅精度高而且运算速度比传统的OMP算法提升超过70%;TSR-L在像素点比较多的情况下能保持比较高的精度,同时速度也比OMP和gOMP算法快,但相比TSR-D速度上还有一定差距。本文进一步研究发现,当稀疏度越高时,TSR-L相比TSR-D有更快的速度,如图9所示,这可能是因为TSR-L在第一步时也是通过逆矩阵求解,而相比之下求解逆矩阵对稀疏度的增加更不敏感。进一步对比本文算法以及OMP类算法的原理,我们发现在进行字典原子的选择时,由于原理不同各自选出的原子可能并不相同,本文算法选出的原子本身和待测像元更相似,所以该方法是合理的。综上,本文提出的两种方法在检测精度,特别是运算速度上相比传统算法有明显提高,并且在稀疏度高低不同的情况下有各自的优势。

图9 不同稀疏度下TSR-D和TSR-L运行时间对比图
4 结束语
本文针对传统稀疏表示重构算法在高光谱目标检测中表现出的运算速度较慢的问题,提出了分步重构算法。该算法舍弃了传统方法使用迭代求解稀疏向量的方法,通过直接求解逆矩阵使得运算简化,从而达到了大幅提升算法运算速度的效果,并且两种方法在稀疏度高低不同的情况下有各自的优势。本文提出的方法简单易行,与传统算法及其改进算法进行目标检测实验对比的结果表明,该算法在保证检测精度不下降的同时大幅提升了运算速度。
[1] 张兵, 高连如. 高光谱图像分类与目标探测[M]. 北京: 科学出版社, 2011: 223, 248.
ZHANG B, GAO L R.[M]. Beijing:,2011: 223, 248.
[2] 杨春伟, 王仕成, 廖守亿,等. 基于核稀疏编码的红外目标识别方法[J]. 红外技术, 2016, 38(3):230-235.
YANG C W, WANG S C, LIAO S Y.An infrared target recognition method based on Kernel Sparse coding[J]., 2016, 38(3): 230-235.
[3] 孙君顶, 赵慧慧. 图像稀疏表示及其在图像处理中的应用[J]. 红外技术, 2014, 36(7): 533-537.
SUN J X, ZHAO H H.Sparse representation and applications in image processing[J]., 2014, 36(7):533-537.
[4] CHEN Yi, Nasrabadi N M, Tran T D. Sparsity-based classification of hyperspectral imagery[C]//2010(IGARSS), 2010: 2796-2799.
[5] CHEN Yi, Nasrabadi N M, Tran T D. Sparse representation for target detection in hyperspectral imagery[J]., 2011, 5(3): 629-640.
[6] Pati Y C, Rezaiifar R, Krishnaprasad P S. Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition[C]//, 1993, 1: 1-3.
[7] Donoho D L, Tsaig Y, Drori I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]., 2012, 58(2): 1094-1121.
[8] WANG J, Kwon S, Shim B. Generalized Orthogonal Matching Pursuit[J]., 2011, 60(12): 6202-6216.
[9] Blumensath, T, Davies Mike E. Stagewise weak gradient pursuits[J]., 2009, 57(11): 4333-4346.
[10] Needell D, Tropp J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]., 2009, 26(3): 301-321.
[11] 赵春晖, 靖晓昊, 李威. 基于StOMP稀疏方法的高光谱图像目标检测[J]. 哈尔滨工程大学学报, 2015, 36(7): 992-996.
ZHAO C, JING X, LI W. Hyperspectral imagery target detection algorithm based on StOMP sparse representation[J]., 2015, 36(7): 992-996.
[12] WANG Y, HUANG S, LIU D, et al. A novel band selection method based on curve area and genetic theory[J]., 2014, 43(3): 193-202.
Target Detection in Hyperspectral Image Using Two Steps Reconstruction Based on Sparse Representation
LIAO Jiajun1,LIU Zhigang1,JIANG Jiangjun1,LU Zhiyong2
(1.,710025,; 2.96831,,100015,)
Aiming at the efficiency problem of traditional reconstruction algorithm for target detection in hyperspectral image, a two steps reconstruction algorithm was proposed.nearest atoms with text pixel were calculated for representing the text pixel to calculate sparse vectors. This method solves the problem by calculating inverse matrix instead of iteration, which simplifies the process. The specific process of the method is given and the method is compared with the traditional and improved ones. Experimental results show that this method can improve the computation speed without decreasing the accuracy of detection.
hyperspectral target detection,reconstruction algorithm,sparse representation
TP75
A
1001-8891(2016)08-0699-06
2016-04-08;
2016-05-17.
廖佳俊(1992-),男,湖南湘潭人,硕士研究生,主要从事遥感图像处理研究。
国家自然科学基金项目(41574008)。

