基于改进型LOG算子的图像增强方法在InGaAs宽光谱红外器件中的应用
葛 朋,李 龙,潘治云,史衍丽
基于改进型LOG算子的图像增强方法在InGaAs宽光谱红外器件中的应用
葛 朋1,2,李 龙1,2,潘治云2,史衍丽1,2
(1.昆明物理研究所,云南 昆明 650223;2.北方夜视技术股份有限公司,云南 昆明 650217)
传统的LOG(高斯-拉普拉斯)算子,由于高斯函数关于中心对称,故它具有各向同性的特点,不能对不同方向的边缘进行有效地检测。基于此,建立并推导了一种改进型的LOG算子,引入了尺度参量和角度参量,改进后的LOG算子是各向异性的,能对不同方向的边缘更有效地检测,从而能更好地增强图像中目标细节。将这种改进后的LOG算子用在InGaAs宽光谱红外器件上,对其所成图像进行图像增强,经过在MATLAB里对于同一幅图像进行比较试验,结果表明相比于传统的高斯-拉普拉斯算子,改进型LOG算子检测到的图像边缘更多,同时对噪声的抑制效果更好,图像细节增强效果更好。
高斯-拉普拉斯算子;图像增强;高斯函数;InGaAs宽光谱器件
0 引言
图像边缘是图像的基本特征之一,图像边缘蕴含了大量图像的方向和形状等内在信息。对图像边缘进行增强旨在加强图像轮廓,突出图像边缘信息,使人们更好地辨识和理解图像所表达的内容[1]。
图像边缘是由于图像中灰度不连续产生的,这种不连续性是随机的,在图像的各个方向,各个角度都有可能发生[2]。同样图像噪声的分布和大小也是随机的。图像边缘以及图像噪声的频率分布大多都在频域的高频部分[3],在进行边缘检测时往往也会加强图像噪声,怎么在准确地检测图像边缘的同时还能做到有效抑制图像噪声一直是图像处理中难点。传统的边缘检测算子有一阶微分算子和二阶微分算子,一阶微分算子如Robert梯度算子、Prewitt算子和Sobel算子等是求取图像的梯度即一阶导数来检测边缘的,而二阶微分算子如Laplace算子和LOG算子等是求取图像二阶导数来检测边缘的,它们都有各自特点。
经典的LOG算子是先对图像进行高斯平滑处理,再进行拉普拉斯边缘检测,相对于其他边缘检测算子具有更好更准确的边缘检测能力。通过深入研究LOG算子原理,推导出了一种具有变尺度、变方向的新的边缘检测算子,并且推导出了引入尺度参量和角度参量的LOG卷积模板的计算方法。仿真实验表明改进后的LOG算子既保留了LOG算子本身的优点,同时还增强了对不同方向边缘的检测能力,对噪声的抑制能力更好。基于此方法,本文将此改进型的LOG算子应用在InGaAs宽光谱器件上,对其成像图像进行图像增强,仿真结果表明相对于传统LOG算子具有更好的增强效果。
1 带尺度、角度分量的LOG算子
1.1 经典LOG算子
高斯-拉普拉斯(LOG)算子源自Marr视觉理论中提出的边缘检测思想,首先对原始图像进行高斯平滑处理,再对平滑后的图像采用拉普拉斯二阶求导求取边缘。其中,平滑处理采用的是二维高斯函数(,):

式中:为高斯函数的空间分布系数。对该函数求拉普拉斯二阶方向导数,即得二维LOG算子的函数形式:
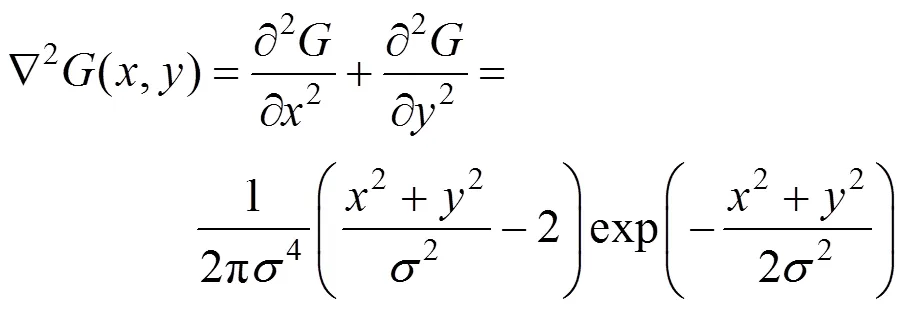
Ñ2呈现圆对称形状,当式(2)中的=0.5时,其形状如图1所示,从三维图像中可以看出,它是关于中心对称的,因此具有各向同性的特征,即当用LOG算子对图像进行边缘检测时,无论取何值,它在各个方向上的边缘检测尺度都是一样的。然而,图像的边缘会出现在各个角度上,对于复杂的图像,其边缘方向更是分布不一样,对不同角度的边缘,应该采用不同的尺度进行检测,这样才能有更好的针对性和效果[4]。
1.2 改进型LOG算子
通过对式(1)二维高斯函数的表达式进行分析,从式(2)中的项-(2+2)/22也可以看出:无论取何值,它对、的影响都是一样的,从而体现了它的各向同性的特点。因此可以在、方向上对取不同的值,引入尺度参量,从而可以让的取值对、的影响不同。

图1 s=0.5时的LOG算子的三维图像
1.2.1 引入尺度参量、
二维高斯函数(,)的基本特征为在方向与方向呈高斯分布,通过三维图像也可以看出。如果将方向与方向上采取不同的尺度,新的高斯函数成了关于中心的椭圆对称。将方向的尺度记为,方向的尺度记为,当>时,椭圆的长轴落在轴上,短轴落到轴上;当<时,椭圆的长轴落在轴上,短轴落到轴上[5]。则根据公式(1)二维高斯函数就变成公式(3):

再对式(3)求拉普拉斯变换(即二阶求导),即可得到变尺度的LOG边缘检测算子:

如图2所示,当=1.5、=1时,从三维图可以看出关于圆对称的LOG算子,变成了关于椭圆对称的形状,并且椭圆的长轴落在轴上,短轴落在轴上。如图3所示,当=1、=1.5时,从三维图看出它也是关于椭圆对称的形状,并且椭圆的长轴落在轴上,短轴落在轴上。
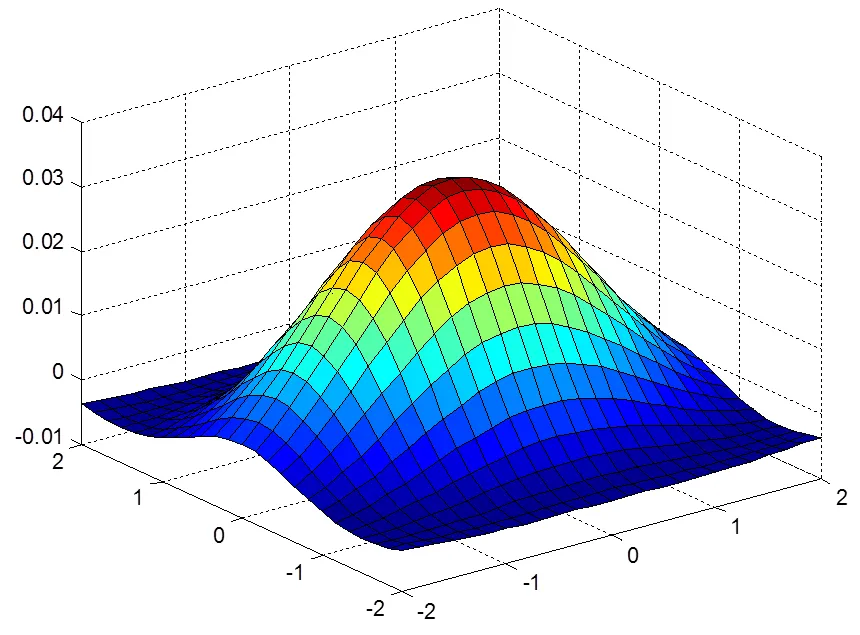
图2 sx=1.5、sy=1时的LOG算子三维图

图3 sx=1、sy=1.5时的LOG算子三维图
1.2.2 引入角度参数
对于一个标准的椭圆,当>时,长轴落在轴上,短轴落在轴上,其表达式是:

现将这个椭圆以坐标原点为中心向逆时针方向旋转a角度,引入一个角度参量a,得到的椭圆形状[6]如图4所示。
旋转角度后,该椭圆坐标关系为:

将式(6)带入标准椭圆表达式(5)中,可以得到以该椭圆方程为:

可以将式(7)的角度参量带入式(3)中,可得引入了角度参量的二维高斯函数表达式:
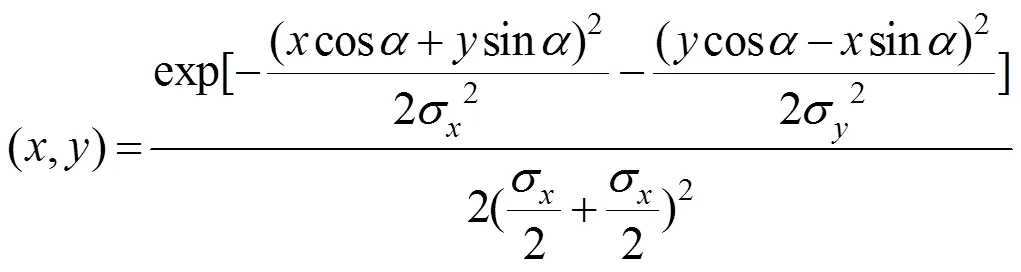
再求式(8)的拉普拉斯变换,得到:

用式(9)生成的卷积模板作用于图像,当取不同的角度值时,即可对不同角度的边缘进行检测。
1.2.3 带有尺度参量、角度参量的LOG卷积模板
LOG模板是将连续的二维LOG算子函数离散化表示,通过建立一个(2+1)×(2+1)的矩阵,只要取值不同,任意大小的LOG模板都能得到[7],其(,)位置的元素值可由式(9)的LOG算子函数确定,将其离散化表示即可得到LOG卷积模板的矩阵形式:

例如当=1.0、=0.8、=2时,取π/4,带入式(10)中,归一化后得到5×5改进型LOG的卷积模板如下:
-0.2197 -0.4968 -0.7349 -0.4558 -0.0723
-0.4968 0.4565 0.9785 -1.0728 -0.4558
-0.7349 0.9785 5.6524 0.9785 -0.7349
-0.4558 -1.0728 0.9785 0.4565 -0.4968
-0.0723 -0.4558 -0.7349 -0.4968 -0.2197
2 试验结果及分析
2.1 改进型LOG算子与传统LOG算子比较
在仿真实验中,首先对比了本文改进型LOG算子和传统LOG算子对Lena图像的增强效果。其中图5(b)采用的LOG模板是由=0.5、=0.4、=2、=π/4得到的,模板矩阵如下:
-0.0000 -0.0005 -0.0009 -0.0000 -0.0000
-0.0005 -0.1038 -0.3472 -0.0341 -0.0000
-0.0009 -0.3472 2.6706 -0.3472 -0.0009
-0.0000 -0.0341 -0.3472 -0.1038 -0.0005
-0.0000 -0.0000 -0.0009 -0.0005 -0.0000
从上面的矩阵可以看出,该矩阵是关于中心位置45°椭圆对称的。图5(c)是由传统的5×5的LOG算子增强后得到的,其中=0.45,模板矩阵如下:
0.1119 0.1123 0.1152 0.1123 0.1119
0.1123 0.3158 1.0102 0.3158 0.1123
0.1152 1.0102 -7.1102 1.0102 0.1152
0.1123 0.3158 1.0102 0.3158 0.1123
0.1119 0.1123 0.1152 0.1123 0.1119
如图5(a)、(b)、(c)所示,采用改进型的LOG算子对Lena原始图像进行增强后的效果明显比采用传统LOG算子增强的效果好,从图5(b)中可以看出,传统LOG算子对噪声也具有加强效果,如从图中的背景可以看出存在明显的颗粒噪声,同时对目标细节容易出现锐化过度的缺陷,如头发细节,帽子细节等;而采用本文改进型的LOG算子得到的图像,不论是图像清晰度还是对噪声的抑制,都要比传统的LOG算子效果好。

图5 改进型LOG算子与传统LOG算子增强效果对比
2.2 改进型LOG算子对不同方向边缘的检测效果验证
用MATLAB对本文提出的改进型LOG算子对不同方向图像边缘检测进行了仿真验证,如图6所示,其中(b)、(c)、(d)、(e)、(f)采用的LOG模板分别是由=0.5、=0.4、=2,分别取0、3p/20,p/4、p/2、3p/4得到的。从图中可以看出,在分别取0、3p/20、p/4、p/2、3p/4时,沿着角度上的边缘很明显地被检测出来,从而验证了含有角度参量的LOG算子在角度取值不同时,能对不同角度的边缘更有效地提取。
2.3 改进型LOG算子在InGaAs宽光谱红外器件的应用
2.3.1 InGaAs宽光谱红外器件图像特点
InGaAs宽光谱红外器件能同时探测可见光和短波红外波段信息[8]。通过把它的光谱响应延伸到可见光,与标准InGaAs短波红外探测器相比,InGaAs宽光谱器件增加了目标对可见光的反射信息,大大丰富了目标的探测信息,实现了类似可见光/短波双波段探测的效果,可有效提高对目标的探测和识别能力[9]。但是InGaAs宽光谱红外器件所成图像仍然存在较大的缺陷,比如目标边缘模糊,目标细节还有待增强等。
如图7所示,(a)、(b)分别是InGaAs宽光谱红外器件对建筑和人脸所成图像。
从图7(a)中可以看出,远处的建筑的细节和2.3km处塔尖已经很难看清楚了;从图7(b)中可以看出,对于人脸成像眼睛和头发细节体现较多,可以看到额头上头发丝的轮廓,但是看不清楚。

图6 不同a值的LOG算子的边缘检测效果图
Fig.6 LOG operator edge detection of rendering with different

图7 InGaAs宽光谱红外器件对建筑和人脸所成图像
2.3.2 改进型LOG算子在InGaAs宽光谱红外器件上的应用
如图8所示,(a)、(b)、(c)、(d)分别是采用改进型LOG算子和传统LOG算子对InGaAs宽光谱红外器件的建筑图像的边缘捡取和增强效果对比。从图8(a)中可以看出改进型LOG算子的边缘捡取更好,而图8(b)中传统LOG算子的边缘捡取相对较少,且对噪声加强程度更大。
从图8(c)和图8(d)中可以看出,传统的LOG算子在增强细节的同时加强了噪声,并且图像整体出现过锐化现象;改进型LOG算子对图像细节增强效果更好,图像更清晰,同时引入的噪声更小,并且相对于原始图像,2.3km处塔尖也清晰可见。
如图9所示,(a)、(b)、(c)、(d)分别是采用改进型LOG算子和传统LOG算子对InGaAs宽光谱红外器件的人脸图像的边缘捡取和增强效果对比。从图9(a)中可以看出改进型LOG算子的边缘捡取更多,而图9(b)中传统LOG算子的边缘捡取相对较少,从两者对盲元区域的加强作用中可以看出传统LOG算子对噪声加强程度更大。
从图9(c)和图9(d)中可以看出,传统的LOG算子在增强细节的同样加强了噪声,并且图像整体出现过锐化现象;改进型LOG算子对图像细节增强效果更好,图像更清晰,同时引入的噪声更小,并且相对于原始图像,人额头上的头发丝更容易识别清楚。

图8 改进型LOG算子和传统LOG算子在InGaAs宽光谱器件中对建筑增强效果对比(sx=1.0、sy=0.8,k=2,a=p/4)

图9 改进型LOG算子和传统LOG算子在InGaAs宽光谱器件中对人脸增强效果对比(sx=1.0、sy=0.8,k=2,a=p/4)
3 结论
建立并推导了一种改进型的LOG算子,通过引入尺度参量和角度参量,能对图像不同方向的边缘更好的捡取,从而更好地增强图像中目标细节。
通过MATLAB对InGaAs宽光谱器件所成图像图像处理的仿真,得到改进型LOG算子检测到的图像边缘更多,同时对噪声的抑制效果更好,经过图像增强处理后的图像细节增强效果更好。
基于改进型LOG算子的各向异性,对不同方向边缘能更准确有效检测的特点,改进型LOG算子适用于低对比度条件下的红外识别与跟踪领域,这方面的应用前景还有待深入研究。
[1] 郑英娟. 基于八方向Sobel算子的边缘检测算法研究[D]. 石家庄: 河北师范大学, 2014.
ZHENG Yingjuan. Edge Detection Algorithm Based on Eight Directions Sobel Operator[D]. Shijiazhuang: Hebei Normal University, 2014.
[2] 陈亮, 郭雷, 高世伟, 等. 一种基于多尺度梯度的边缘提取方法[J].计算机应用, 2008, 28(12): 3129-3133.
CHENG Liang, GUO Lei, Gao Shiwei, et al. An edge detection method based on multi-scale gradient[J]., 2008, 28(12): 3129-3133.
[3] 黄剑玲, 邹辉. 基于高斯Laplace算子图像边缘检测的改进[J]. 微电子学与计算机, 2007, 24(9): 155-157.
HUANG Jianling, ZHOU Hui. Improvement of image edge detection based on Gauss Laplace Operator[J]., 2007, 24(9): 155-157.
[4] 严国萍, 何俊峰. 高斯-拉普拉斯边缘检测算子的扩展研究[J]. 华中科技大学学报: 自然科学版, 2006, 34(10): 21-23.
YAN Guoping, HE Junfeng. Extended Laplacian of Gaussian Operator for edge detection[J]., 2006, 34(10): 21-23.
[5] 何俊峰. 基于视觉原理的图像边缘检测算子研究[D]. 武汉: 华中科技大学, 2006.
HE Junfeng. Based on the Principle of Visual Image Edge Detection OperatorResearch[D]. Wuhan: Huazhong University of Science and Technology, 2006.
[6] 陈银平, 涂碧海, 张毅, 等. 改进型LOG算子在偏振片绝对角度中的应用[J]. 计算机技术与发展, 2014, 24(5): 164-167.
CHEN Yinping, XU Bihai, Zhang Yi, et al. The application of modified LOG operator in absolute angle of polarizer[J]., 2014, 24(5): 164-167.
[7] 赵磊. 基于图像处理的贴片电阻缺陷检测方法研究与应用[D]. 南京: 南京邮电大学, 2013.
ZHAO Lei. Research and Application on SMD Resistor Defect Detection Method Based on Image Processing[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2013.
[8] 张卫锋, 张若岚, 史衍丽, 等. InGaAs短波红外探测器研究进展[J].红外技术, 2012, 34(6): 361-365.
ZHANG Weifeng, ZHANG Ruolan, SHI Yanli, et al. Development process of InGaAs short-wave infrared focal plane arrays[J]., 2012, 34(6): 361-365.
[9] 史衍丽, 李龙, 葛朋, 等. 高性能InP/InGaAs宽光谱红外探测器[J]. 红外技术, 2016, 38(1): 1-5.
SHI Yanli, LI Long, GE Peng, et al. High performance InP/InGaAs wide spectrum infrared detectors[J]., 2016, 38(1): 1-5.
Image Enhancement Method Based on Modified LOG Operatorin the Application of InGaAs Wide Spectrum Infrared Device
GE Peng1,2,LI Long1,2,PAN Zhiyun2,SHI Yanli1,2
(1.,650223,; 2..,650217,)
Traditional LOG(Gauss-Laplacian) operator, as a result of which the Gaussian function is symmetrical about the center, it is isotropic, unable to effectively detect the edge of different directions. Based on it, a modified LOG operator has been set up and derived. Owing to the introduction of the scale parameter and angle parameter, the improved LOG operator has the characteristics of anisotropy, on the edge of the different directions it can better effectively detect, which can better enhance image target in details. Using the modified LOG operator in the InGaAs wide spectrum infrared device to enhance its image, after comparison test for the same image in MATLAB, results show that compared with the traditional Gauss-Laplacian, the improved LOG operator detect image edges more, at the same time it is better for noise suppression and image detail enhancement effect.
Gauss-Laplacian,image enhancement,Gauss function,InGaAs wide spectrum infrared device
TN215,TN911.73
A
1001-8891(2016)08-0670-08
2016-05-31;
2016-06-24..
葛朋(1992-),男,硕士研究生,主要研究方向为红外图像处理技术。E-mail:542851112@qq.com。
史衍丽(1969-),女,研究员,博士生导师,博士,主要研究方向为探测器研究与制备。E-mail:ylshikm@hotmail.com。
云南省重点基金项目(2015FA00);昆明市科技计划项目(2015-2-R-01728);云南省应用基础研究计划重大项目(2016FC002)

