机载红外系统主反射镜的拓扑优化设计
李 蕾,张 葆,李全超
机载红外系统主反射镜的拓扑优化设计
李 蕾1,2,张 葆1,李全超1
(1. 中国科学院长春光学精密机械与物理研究所 中国科学院航空光学成像与测量重点实验室,吉林 长春 130033;2. 中国科学院大学,北京 100049)
反射镜轻量化设计一直是光机结构设计领域的一项挑战性课题。针对某机载红外光学系统的主反射镜,提出了一种基于SIMP拓扑优化方法的反射镜轻量化设计流程,建立了反射镜拓扑优化的数学模型,以最小化镜体自重和抛光载荷作用下的镜面矢高位移RMS值为优化目标,同时考虑对称约束和拔模约束,对反射镜进行了拓扑优化设计。根据拓扑优化结果设计了新的反射镜轻量化结构,并将其与传统结构进行了对比。采用拓扑优化方法设计的反射镜具有更高的轻量化率,同时能够获得较高的面形精度。
红外系统;主反射镜;轻量化设计;拓扑优化
0 引言
机载红外系统是载机进行目标探测、搜索、警戒、预警的重要设备,在现代空战中起着举足轻重的作用[1]。为实现高灵敏度、大视场、高空间分辨率要求,现代红外光学系统一般采用大口径折反式系统。主镜作为系统中的主要部件,其镜面面形直接影响了系统成像质量。此外,机载环境对载荷重量有极其严格的要求,因此,在尽量减轻镜体重量的同时,使镜面在自重、加工载荷等外部载荷的作用下的面形精度满足设计要求,具有十分重要的意义。
传统的反射镜轻量化结构多为三角形、扇形和六边形轻量化孔形式,针对这种布局固定的结构,进行优化设计时仅以加强筋的截面尺寸和形状、轻量化孔尺寸等作为优化变量,存在着不能改变结构拓扑的缺陷,优化效果十分有限。
随着近年来结构优化技术的发展,连续体拓扑优化方法开始被应用于反射镜轻量化设计。Shutian Liu等人[2]将拓扑优化方法应用于大口径空间反射镜的设计,在考虑拔模约束和抛光载荷的条件下,提出了一种单元分组策略,获得了材料的最优化空间分布,但是其优化过程以结构整体刚度为优化目标,没有直接考虑光学性能指标。Kang-Soo Park等人[3]在优化过程中以镜面面形误差RMS为优化目标,但是仅能获得反射镜背部材料的平面分布。
针对现有方法的不足,本文将拓扑优化方法应用于某机载红外系统的主反射镜轻量化设计中,以最小化镜面面形误差为优化目标,设计了新的反射镜轻量化结构,并将其与传统结构进行了对比。
1 反射镜拓扑优化的数学描述
1.1 连续体拓扑优化方法
目前常用的连续体拓扑优化方法有均匀化法[4]、SIMP法(Solid Isotropic Material with Penalization,各项同性材料惩罚模型)[5]、渐进结构优化法[6]、水平集法[7]等。其中,SIMP法具有单元设计变量描述简单、便于实施的优点,是当前应用最成熟的方法。
SIMP法又称为人工材料法(Artificial Material Method)或密度法(Density Method),该方法引入一种密度可变材料,以在[0, 1]范围内连续变化的单元相对密度为设计变量。迭代过程中,为了抑制中间密度单元,获得相对密度成0-1分布的清晰结构,SIMP法采用如下材料插值模型惩罚中间密度单元:
E=xE0,>1,∈[0, 1] (1)
式中:E为弹性张量;E0为实体材料的弹性张量;为单元相对密度(=/0,为单元实际密度,0为实体材料密度);为惩罚因子,用于惩罚中间密度单元。通过选取大于1的惩罚因子,可降低中间密度材料对弹性张量的贡献程度,使设计结果趋近于0-1分布。已有文献证明,惩罚因子的取值应不小于3[5],能够获得一个比较理想的结果。式(1)建立了单元相对密度与弹性张量的直接关系函数,拓扑优化问题就转化为以相对密度为设计变量的尺寸优化问题,能够采用传统的准则法、数学规划法、移动渐近线法(MMA)等进行求解。
1.2 优化问题的数学模型
以某机载红外系统的主反射镜为设计对象,该系统采用同轴折反式光学系统,主镜外径400mm,中心孔径100mm,镜厚55mm。镜体材料选用铝合金6061,其具体参数详见表1。铝合金材料密度小、重量轻,并且具有优异的加工性能,可直接在镜体背部加工出复杂的轻量化孔和支撑结构,极大地缩短了加工周期,降低了加工成本[8-9]。

表1 铝合金6061参数表
反射镜采用背部三点支撑,Vukobratovich[10]给出了三点支撑的最优支撑半径为0.645max,此时反射镜在重力作用下面形误差PV值最小,本例支撑半径为129mm。
反射镜拓扑优化的目标是在满足载荷重量要求的前提下,设计出使镜面变形最小的反射镜轻量化结构。优化过程中,将反射镜水平放置,此时镜面变形主要由反射镜自重导致。此外,考虑加工载荷,尤其是镜面抛光过程中的抛光压力,可能导致镜面出现较大局部变形,严重影响反射镜的光学性能。因此,设计过程中要同时考虑重力载荷和抛光压力的影响。
光学表面变形一般用面形误差的峰谷值(PV)和均方根值(RMS)来定量描述,而表面变形通常可以用去除刚体位移后的矢高位移(即沿光轴方向位移)或表面法向位移来表示[11],其RMS值可表示为:
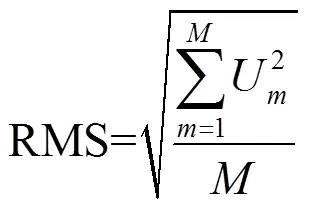
式中:为光学表面节点总数;U为第个节点处的矢高位移或法向位移。
光学表面误差和光学系统波前差之间的关系存在着简单的表达式,在被一个变形的光学表面反射后,光线的波前误差为:
WFE=2scos(3)
式中:WFE为波前差;s为光学表面误差;为入射角。因此,光机集成分析中通常利用光学表面误差RMS和PV值来对光学表面变形对光学系统性能的影响进行定量描述。
现有文献中多以结构整体刚度、固有频率等间接指标作为优化目标,本文直接以最小化矢高位移RMS值为优化目标,优化过程中直接考虑光学性能指标。设计约束选取为反射镜体积。此外,考虑反射镜的外形和加工条件,还应考虑一些工艺约束,如对称约束、拔模约束等。
综上所述,基于SIMP材料插值模型的反射镜拓扑优化问题,其数学表达形式为:

式中:是由设计变量所组成的向量;x表示第个单元的相对密度;为单元总数;()为目标函数;为光学表面节点总数;U为第个节点处的矢高位移;V表示第个单元的体积;*是事先指定的体积上限;min是单元相对密度的下限值。这是一种“软杀”(soft kill)方法,空单元并不是从结构中直接删除,而是用一种弱材料代替。采用这种方法的原因是:设计过程中,每一步迭代都需要根据上一步中结构的有限元分析结果来判断单元的添加或删除,采用弱材料替代空单元,就可以将这些“空单元”包含到分析过程中,为下一步迭代提供必要的信息。
优化过程中,采用单元灵敏度作为更新设计变量的依据。灵敏度是目标函数相对于设计变量的导数,可以衡量设计变量的变化对目标函数产生的影响。对于式(4)所描述的问题,单元灵敏度定义为矢高位移RMS值相对于单元设计变量的导数:

2 反射镜拓扑优化设计的应用
2.1 反射镜设计模型
反射镜初始设计模型如图1所示,模型采用C3D8R(八节点六面体减缩积分)单元进行离散,单元数16371,节点数19605。将支撑孔和镜面(6.5mm)区域定义为非设计区域,其他区域均为设计区域。

图1 初始设计模型
定义反射镜光轴方向为竖直方向,镜面朝上,背部3个支撑孔施加固支约束。镜体承受重力载荷(=9.81N/kg),同时在镜面施加均布载荷0.2kPa,模拟抛光压力。其他设计参数定义为:*=0.30(0为初始模型体积),=3,min=0.001,即相对密度低于0.001的单元视为空单元,同时施加对称约束和拔模约束。
拓扑优化流程如图2所示,本文采用Abaqus/ATOM进行优化求解,每次迭代首先对结构进行一次有限元分析,然后根据有限元分析结果计算单元灵敏度,并更新单元相对密度。

图2 优化设计流程
2.2 设计结果分析和对比
优化过程经历45次迭代达到收敛,最终获得拓扑优化结果如图3所示。拓扑优化仅能给出大致的材料分布,从图中可以看到材料分布在3个支撑点内侧形成一个六边形布局,每个支撑点位置向镜体边缘伸出两条平行的加强筋,且距离支撑点越远,高度越低。
显然,拓扑优化结果难以直接应用于实际生产,且筋板结构存在不连续处,需要根据实际加工条件,进行重新设计,新的轻量化反射镜形式如图4所示,该结构轻量化率达到72.8%。

图3 拓扑优化结果
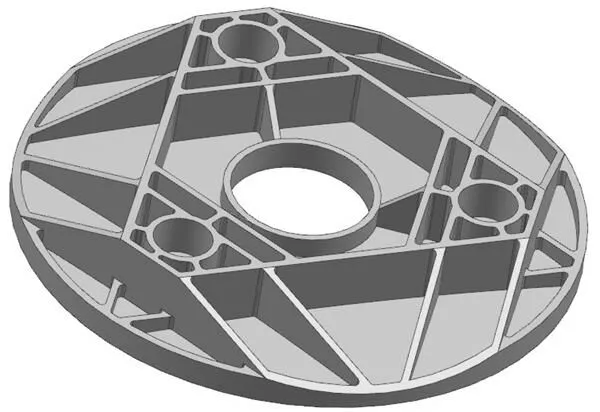
图4 拓扑优化后的轻量化反射镜
根据2.2中所述,利用面形误差PV和RMS值,可定量评价光学表面变形对光学系统性能的影响。为了比较拓扑优化后反射镜的PV和RMS值,建立了如图5所示的对比模型,采用传统的三角形轻量化孔形式,轻量化率为61.7%,小于拓扑优化结果。在轴向和径向重力载荷作用下对两种结构进行了对比分析,通过面形拟合获得了镜面变形PV值和RMS值。为验证结构的动态刚度,对其进行了模态分析。此外,考虑机载低温环境,分析了环境温度-20℃和-40℃条件下的镜面变形。对比分析结果如表2所示。

图5 传统轻量化结构
轴向重力载荷是拓扑优化所采用的工况,镜面变形如图6所示。该工况下拓扑优化结构的面形误差PV值为99.5nm,RMS值为23.9nm,均小于采用三角形轻量化孔的结构。
径向重力加载条件下的镜面变形如图7所示。该工况下传统结构的镜面面形略优于拓扑优化结构。这是由于拓扑优化时的工况是轴向重力加载,未考虑径向重力载荷,但是两种结构的镜面变形RMS值分别仅为6.0nm和4.1nm,相差不大,且远低于光学设计公差,完全满足设计要求。
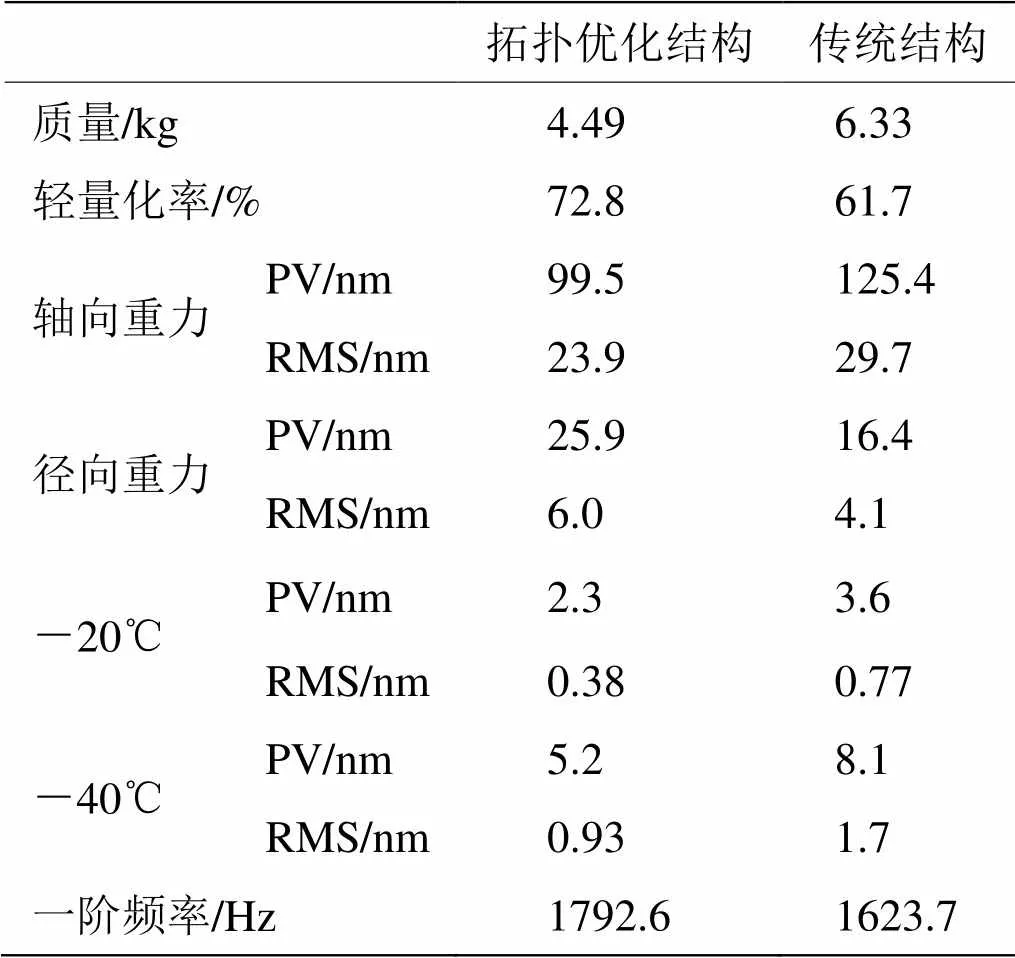
表2 分析结果对比

图6 拓扑优化结构(左)和传统结构(右)在轴向重力加载下的镜面变形云图

图7 拓扑优化结构(左)和传统结构(右)在径向重力加载下的镜面变形云图
针对机载低温环境,分析了-20℃和-40℃条件下的镜面变形。结果表明,随着温度降低,镜面面形误差RMS和PV值均增大,且拓扑优化结构的镜面面形略优于传统结构。然而,温度变化导致的面形误差RMS值和PV值都很小,相对于重力的影响可忽略不计。由于反射镜采用铝合金材料,因此只需将支撑结构选用相同的材料,即可使结构具有较高的温度适应性,将温度变化对镜面变形的影响降至最低。
模态分析结果表明,拓扑优化结构的一阶固有频率也高于传统结构,表明其具有更高的动态刚度。注意到,两种结构的固有频率数值都较大,这是由于模态分析时,仅对反射镜在背部三点固支条件下进行分析,未考虑支撑结构的影响。
综上所述,采用拓扑优化方法获得的反射镜轻量化方案由于传统的轻量化结构。
3 结论
采用SIMP法,以镜面矢高位移RMS值为优化目标,对机载红外系统主反射镜进行了拓扑优化设计,设计的反射镜在满足结构轻量化的同时获得了较高的面形精度。镜体轻量化率达到72.8%,镜面面形误差RMS值仅为23.9nm,满足设计要求,且优于传统轻量化结构。
利用拓扑优化方法进行反射镜轻量化设计设计,克服了传统设计方法的盲目性和参数化设计的局限性,极大提高了设计效率。
[1] 申洋, 唐明文. 机载红外搜索跟踪系统(IRST)综述[J]. 红外技术, 2003, 25(1): 13-18.
SHEN Yang, TANG Mingwen. An overview of infrared search and track (IRST)system[J]., 2003, 25(1): 13-18.
[2] LIU S, HU R, LI Q, et al. Topology optimization-based lightweight primary mirror design of a large-aperture space telescope[J]., 2014, 53(35): 8318-25.
[3] Park Kang-Soo, Lee Jun Ho, Youn Sung-Kie. Lightweight mirror design method using topology optimization[J]., 2005, 44(5): 053002.
[4] Bendsoe MP, Kikuchi N. Generating optimal topology in structural designusing a homogenizationmethod[J]., 1988,71:197-224.
[5] Bendsoe M P.-[M]. Springer, 2003.
[6] HUANG X, XIE Y M. A further review of ESO type methods for topology optimization[J]., 2010, 41(5): 671-683.
[7] Michael Y W, WANG X M, GUO D M. A level set for structural topology optimization[J].2003, 192: 227-246.
[8] 张东阁, 傅雨田. 铝合金反射镜的发展与应用[J]. 红外技术, 2015, 37(10): 814-823.
ZHANG Dongge, FU Yutian. Development and application of aluminum mirrors in optical system[J]., 2015, 37(10): 814-823.
[9] 范磊, 赵勇志, 曹玉岩. 红外离轴系统金属反射镜设计与分析[J]. 红外技术, 2015, 37(5): 374-379.
FAN Lei, ZHAO Yongzhi, CAO Yuyan. Design and analysis of metal mirror for infrared off-axial system[J]., 2015, 37(5): 374-379.
[10] Vukobratovich D. Optimum Shapes for Lightweighted Mirrors[C]//, 1982, 332: 419-432.
[11] Keith B Doyle, Victor L Genberg, Gregory J Michels.[M]. 2ndedition,, 2012.
Topology Optimization of Primary Mirror in Airborne Infrared System
LI Lei1,2,ZHANG Bao1,LI Quanchao1
(1.,,,,130033,; 2.,100049,)
The lightweight design of mirror has always been a challenging task in the field of opto-mechanical structure design. For the lightweight design of the primary mirror in an airborne infrared optical system, a lightweight mirror design procedure is proposed based on the SIMP topology optimization method. The mathematical model of topology optimization is established. With the objective of minimizing the RMS value of surface sag displacements under the load of gravity parallel to the optical axis and polishing pressure, the mirror is optimized by using topology optimization method while symmetry and casting constraint considered. According to the topology optimization result, a new lightweight mirror configuration is designed. The proposed mirror is compared with a traditional lightweight structure. The comparison results show that the lightweight ratio of the mirror obtained by using topology optimization method is higher than the traditional one. And a high optical surface accuracy can be achieved.
infrared system,primary mirror,lightweight design,topology optimization
TH745
A
1001-8891(2016)08-0648-05
2016-02-02;
2016-04-05.
李蕾(1989-),男,研究实习员,主要研究方向为结构优化设计。
国家自然科学基金青年科学基金项目(61405192)。

