换热网络多目标综合优化算法研究进展
吕俊锋,肖武,王开锋,李中华,贺高红(大连理工大学精细化工国家重点实验室,膜科学与技术研究开发中心,辽宁 大连 116024)
换热网络多目标综合优化算法研究进展
吕俊锋,肖武,王开锋,李中华,贺高红
(大连理工大学精细化工国家重点实验室,膜科学与技术研究开发中心,辽宁 大连 116024)
摘要:资源和能源的可持续发展使得换热网络综合不仅要考虑经济性,同时要满足柔性、可靠性、可操作性和环境影响度等指标的要求。目前,换热网络多目标综合的研究有了初步进展并引起了广泛关注。本文阐述了进行换热网络多目标综合的必要性并总结了相关研究。重点对常用的多目标优化算法作了总结和对比,综述了其在换热网络多目标优化设计中的应用进展。研究表明,传统多目标算法越来越无法满足复杂模型的求解,而多目标进化算法可以很好地求解换热网络综合多目标优化问题,其中NSGA-Ⅱ算法是目前应用最广的有效算法。提出尝试NSGA-Ⅱ等多目标进化算法,基于超结构建立包括经济性、柔性、可靠性、可操作性和环境影响度等在内的换热网络多目标综合模型,给出Pareto最优解集合供决策者选择是未来的研究方向。
关键词:系统工程;优化设计;换热网络;多目标;算法;NSGA-Ⅱ
第一作者:吕俊锋(1992—),男,硕士研究生,主要从事过程系统优化研究。联系人:肖武,副教授,硕士生导师,主要从事化工系统工程和过程强化的研究。E-mail wuxiao@dlut.edu.cn。
换热网络综合是过程系统工程(PSE)的一个重要分支,从20世纪70年代爆发石油能源危机之后,换热网络综合开始引起广泛的关注[1]。一直以来,对换热网络综合的研究主要以节能降耗和降低年度总费用为目标。然而,近年来随着资源和能源可持续发展步伐的不断加快,人们不再仅仅关注换热网络的经济性指标,同时对柔性、可靠性、可操作性和环境影响度等指标的要求也随之增长。因此越来越多的学者开始从多目标的角度进行换热网络综合。
在换热网络综合中,一些问题是由多个目标组成,并且各个目标之间通过变量相互影响、相互制约。因此综合的权衡换热网络的各个目标,进行换热网络多目标综合,给决策者提供多个Pareto解的选择方案具有非常重要的现实意义[2]。然而虽然多目标优化理论在化工领域的应用越来越广泛,但是将其应用于换热网络综合的研究仍然停留在理论阶段[3]。这是因为在换热网络多目标综合中,为了降低模型求解的复杂度作了很多假设和简化,导致结果偏离工程实际应用。
目前,国内外已发表的换热网络多目标综合的文献中,常用的多目标优化算法主要有加权求和法、ε-约束法、NIMBUS法和NSGA-Ⅱ算法。模型中目标函数不仅有换热单元数目、换热面积、公用工程消耗量等经济性目标,还包括环境影响度和柔性等目标。将可靠性和可操作性等目标函数加入到模型之中,以及尝试更多优秀的多目标优化算法仍然有待于进一步研究。
本文阐述了进行换热网络多目标综合的必要性,对已发表的换热网络多目标综合的文献进行了概括总结,并对其中常用的多目标优化算法进行了对比分析。以期为从事换热网络多目标综合相关研究的学者在模型建立和算法选择方面提供参考。
1 必要性及问题描述
1.1 换热网络多目标综合的必要性
在以往换热网络综合的研究中,很多学者从单目标优化的角度考虑了换热网络的可靠性、柔性、可操作性和环境影响度等指标。
YI等[4]提出了同时满足换热网络柔性和可靠性指标的两步渐进式方法。第一步利用虚拟T-H图,初步综合得到能够满足柔性指标的换热网络结构,第二步通过网络解耦提高可靠性,使换热网络的可靠性不低于0.9,以总费用为目标函数,采用GA/SA算法求解,最后求出在满足柔性和可靠性指标的约束条件下总费用最低的网络结构。ESCOBAR等[5]提出了同时满足换热网络柔性和可操作性指标的优化模型,为了降低计算的复杂度,采用静态分析法和一些线性假设简化模型,在GAMS软件环境下对总费用进行优化。WEN和SHONNARD[6]建立了同时考虑经济性和环境影响度的数学模型,对7个生命周期影响评估指标(LCIA)环境影响指标进行标准化,然后经过权衡计算得出复合环境影响评价指标(IPC),采用层次分析法(AHP)将IPC指标与经济性指标合并,计算得出经济性和环境影响度两个指标所占权重分别是0.82和0.18。对最小传热温差进行优化,并通过案例中的灵敏度分析说明了不同因素对最小传热温差的影响程度大小。CHEN和HUNG[7]以YEE和GROSSMANN的分级超结构模型为基础,建立了一个同时考虑柔性、最低公用工程消耗量和最少换热单元数的模型,采用两级模糊决策的方法将多目标问题转化为单目标优化的问题,在GAMS和CPLEX软件环境下进行求解。
上述文献以单目标优化的角度,在优化总费用的同时考虑了多个指标,在一定程度上是一种改进。但其缺陷也很明显,BJÖRK和WESTERLUND[8]说明了由于模型中具有二元变量,仅仅通过改变年度费用权值因子的单目标优化方法无法获得完整的优化解。然后提出多目标优化中的Pareto曲线能够更好地描述多个目标之间的权衡,并且能够提供多个选择方案,更贴近实际应用。SREEPATHI和RANGAIAH[9]提出在客观条件以及实际操作环境的限制下,单目标优化得到的结果只是理论上最优,无法满足实际工况的多方面要求,并且通过数据说明了换热面积、换热设备数量和公用工程消耗这3个费用目标处于相互竞争、相互影响的状态,指出通过多目标优化得出的非支配解集能够更好地兼顾各个费用目标,进一步说明换热网络多目标综合的必要性。
1.2 换热网络多目标综合的问题描述
一般地,换热网络多目标综合问题可以描述成如式(1)~式(3)形式[10]。

式中,x是变量,包括浓度、温度、流量、压力和设备尺寸等;f(x)是目标函数的集合;fp(x)是换热网络相应的公用工程费用、换热单元数目、换热面积、可靠性、柔性、可操作性和环境影响度等目标函数;gi(x)和hj(x)是流股和换热器的热平衡、流股质量和热量衡算、最小传热温差、连续变量非负等约束条件[11];I是不等式约束条件;J是等式约束条件。
经过多目标优化得到的一系列解称为非支配解(non-dominated solutions)或Pareto最优解,并且这些非支配解之间无法比较优劣[12],而单目标优化通常得出的是唯一解,这是两种优化方法的本质区别。如图1是对年度总费用和环境影响度[13]两个目标函数进行换热网络多目标综合获得的Pareto曲线,位于Pareto曲线上的点是Pareto最优解,位于曲线上侧的是次优解,位于曲线下侧的是不可行解。通过曲线可以很好地权衡比较两个目标,避免了单目标优化顾此失彼的弊端,同时给决策者提供多个选择方案,方便决策者根据实际情况选择最佳方案。
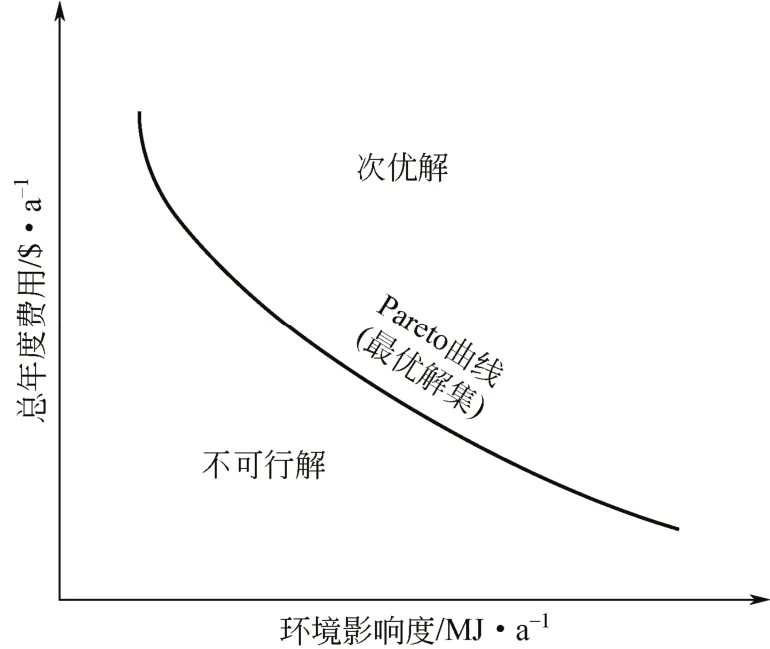
图1 Pareto曲线[13]
2 换热网络多目标综合中常用算法
在进行换热网络多目标综合时[14],第一步是根据换热网络的物理特性建立一个由约束条件和目标函数组成的数学模型;第二步是选择合适的多目标优化算法对所建立的模型进行求解,从而求得在满足约束条件的前提下,使多个目标函数都得到优化的Pareto解集。换热网络多目标综合中常用的多目标优化算法分为两类,第一类是包括加权求和法、ε-约束法和NIMBUS法在内的传统多目标算法,第二类是以NSGA-Ⅱ为代表的多目标进化算法[15]。下面结合常用算法对换热网络多目标综合的相关研究进行总结。
2.1 加权求和法
这种方法是给各个目标函数分配权重,然后通过加权求和的方法,将多目标优化问题转化为单目标优化问题进行求解[15],表示如式(4)。
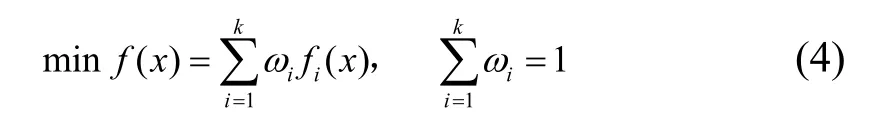
式中,ωi是权重,不同的权重分配,经过计算可以得到不同的Pareto最优解。其优点是求解简单,便于计算,容易理解;缺点是权重的选择主观性较大,多个目标间不可比较,并且Pareto前沿非凸时此方法无法求解。
WEN和SHONNARD[6]应用该方法对换热网络的环境影响度和经济性指标进行了评估。JIN等[16]建立了同时考虑环境影响度和经济性的数学模型,分别将环境影响度和经济性指标除以相应条件下的最大值,从而将两个不同量纲的目标函数转化为标量函数,然后针对这两个标量采用加权求和的方法求解,将多目标问题转化为单目标问题,最终结果使每年污染物排放量降低了68.07%。
2.2 ε-约束法
其原理是选取某个目标函数作为优化目标,而将其余的目标函数作为约束条件,转化为单目标优化问题后,用单目标算法求解[17]。表达式如式(5)、式(6)。

该方法的优点是解算简单,易实现,在优化过程中h取不同的值,计算可得多个Pareto最优解;缺点是ε值难以选取,需要未知的先验知识。
LÓPEZ-MALDONADO等[13]应用该算法对建立的mo-MINLP换热网络多目标综合模型进行求解,模型中目标函数包括年度费用和环境影响度,采用eco-indicator 99作为环境影响度的指标,实现了换热网络经济性和环境影响度的多目标综合。VASKAN等[18]指出仅仅采用经过整合的单一指标(例如eco-indicator 99等)并不足以评价环境影响度,因此采用了应用更广泛的LCA量化环境影响,建立了以总费用和环境影响度为目标函数的MINLP模型,在求解模型过程中,同样采用了ε-约束法,通过改变ε的值并多次运行,获得了不同的Pareto解。案例中包含12个目标函数(总费用和11个LCA环境影响度目标),采用降维法分析并移除多余的目标,从而在不改变结构的前提下降低了求解问题的复杂度。将案例优化结果与文献[13]的结果进行对比,说明了选取LCA可以更有效地评价环境影响度,更好地实现了换热网络经济性和环境影响度的多目标综合。
2.3 NIMBUS法
NIMBUS是一种交互式规划的方法[19],这种决策方法可以使决策者参与到模型的优化与求解中,即分析和决策交替进行,主要思想是在每一步交互过程中,决策者根据对目标函数的满意程度对其进行分类,引导算法向指定区域搜索,无需给出具体的偏好信息(例如目标的排序和权重等),并且可以充分利用决策者的专业知识和经验。NIMBUS可以求解不可微分和非凸的多目标优化问题,不受目标函数的数目影响,同时这种多目标优化方法在互联网上有在线平台。但是这种算法仍是将多目标问题转化为单目标子问题进行求解,与加权求和法相比,只是更好地考虑了决策者的偏好,其本质依然是单目标优化。
LAUKKANEN等[20]采用了这种NIMBUS交互式多目标优化的方法,以YEE和GROSSMANN的超结构模型为基础,以换热单元数目、总换热面积、冷热公用工程消耗量为目标函数,进行了换热网络的多目标综合,通过NIMBUS将多目标问题转化为单目标问题,然后在GAMS软件系统中进行求解。对两个案例进行了优化,通过案例一优化了总费用,同时协调了各个目标,并说明了单目标优化无法得到非支配解,案例二使总费用降低了32%。随后,LAUKKANEN等[21]采用经过简化的NIMBUS将多目标问题标量化为一个单目标函数,然后在GAMS环境下对标量化的单目标函数进行求解,结合双层优化策略,实现了对中等规模换热网络的多目标综合。
2.4 NSGA-Ⅱ算法
2002年,DEB等[22]提出了第二代基于非支配排序的遗传算法(NSGA-Ⅱ),NSGA-Ⅱ算法性能优良,主要对NSGA进行了三点改进[23]:首先是引入精英保留策略,提高了算法的收敛性;其次改进了非支配排序的算法,使时间复杂度从O(mN3)降低到O(mN2),提高了算法效率;另外采用拥挤度比较算子代替了共享策略,解决了需要人为确定共享参数的缺点。迄今为止,NSGA-Ⅱ是最优秀的多目标优化算法之一。在进化多目标优化的领域,DEB提出 NSGA-Ⅱ的文献被引用次数最多[24],目前被引用次数达到了14000余次。
AGARWAL和GUPTA[25]首次将NSGA-Ⅱ算法应用于换热网络综合,摆脱了启发探试的方法,采用NSGA-Ⅱ算法并引入交叉算子,同时结合sJG转位子加快算法的收敛速度。目标函数包括年度费用、公用工程消耗、能量回收率和换热单元数量。文献中并没有同时对这4个目标函数进行优化,而是分别选取了其中2个和3个目标函数,分别进行换热网络双目标和三目标综合,指出NSGA-Ⅱ更适合于求解双目标优化问题,并通过多个案例对比,说明通过多目标优化得到的非支配解集优于单目标优化的唯一解。任建强[26]以成本和火积耗散数为目标函数,同样采用NSGA-Ⅱ算法实现了对换热网络成本和换热效果的多目标优化。林露[27]建立了以环境影响度、公用工程费用和投资费用为目标函数的换热网络多目标综合MINLP模型,在模型引入温差修正系数,并且去除了等温混合的不合理假设。采用IPCC方法,同时结合全球变暖潜值(GWP),以温室气体排放量作为环境影响度的衡量标准,这种方法是从局部衡量换热网络的环境影响度。在MATLAB-GUI平台上,基于换热网络综合软件系统HenDesign,开发了采用NSGA-Ⅱ算法的换热网络多目标综合的模块。根据建立的换热网络多目标综合模型和NSGA-Ⅱ求解方法,对3个案例进行了换热网络的综合,每个案例均获得了令人满意的结果。
2.5 算法对比
传统多目标优化算法[29]本质是采用一些技术和方法将多个目标函数转化成单目标函数,然后以单目标优化方法进行求解。其缺点主要有:对目标函数有连续性、凸性、线性等要求;为了得出多个Pareto最优解,需要多次独立运行求解,增加了计算时间,计算结果难以比较;在分配权重系数或者惩罚值时,需要人为规定,主观性较大。
近年来多目标进化算法[30]在求解多目标优化问题的应用中展现了良好的前景,其在换热网络综合中的应用也是目前的研究热点。遗传算法3个方面的优点[31]使得它非常适用于求解多目标优化问题:首先,进化算法以种群进化为基础使其具有搜索的全局性和多向性特点,算法运行一次便能得到多个Pareto最优解;其次,进化算法通过个体之间支配关系决定个体的适应度值,不需要为各个目标配置权重;最后,进化算法可以处理所有类型的约束条件和目标函数,不需要满足连续性、凸性和线性等数学条件。
然而虽然多目标进化算法在多目标问题的求解上取得了非常好的成效,但是这并不意味着多目标进化算法会彻底取代传统多目标算法[32]。多目标进化算法的理论研究仍有很多不成熟的地方,比如其早熟问题还没有得到解决、缺少收敛性证明以及参数设置比较困难等。相反,传统多目标优化算法仍然具有很大的优势,比如易实现、计算量小、计算速度快、设计简单、容易理解、方便建立数学模型等。
换热网络多目标综合中常用的多目标算法比较如表1所示。可以看出,在换热网络多目标综合中,综合的考虑各个算法的优点和缺点,选择合适的算法至关重要。对于目标函数满足连续性、凸性、线性要求的简单模型,传统多目标优化方法仍不失为一种简单易行的方法。然而为了贴近工程实际,需要考虑很多复杂因素的换热网络,其数学模型经常呈现严重的不连续性、非凸性和非线性,具有全局最优性的多目标进化算法是求解这类问题的非常好的选择[28]。虽然NSGA-Ⅱ算法已经应用到换热网络多目标综合,然而仍然还有很多优秀的算法有待于尝试。为了更贴近工程实际需要,应该尽可能减少各种假设和简化,建立符合生产实际的详细数学模型,并采取更有效的算法对模型进行求解。
3 结语与展望
3.1 结语
虽然通过单目标优化的方法可以考虑换热网络柔性、可靠性、可操作性和环境影响度等约束条件,但是换热网络多目标综合可以将这些约束与经济性放在一起作为目标函数同时进行优化,具体优势体现在以下方面。
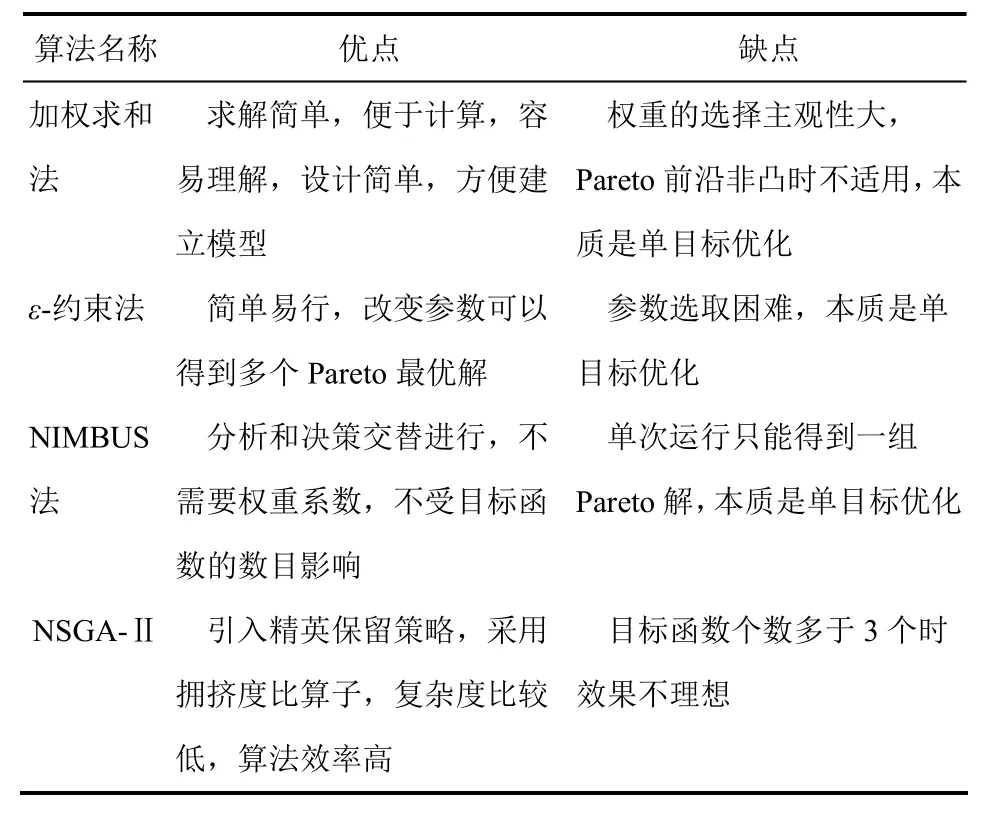
表1 换热网络多目标综合中常用的多目标算法
(1)单目标优化得到的唯一解很难满足工程实践多元化的要求,而通过换热网络多目标综合得到的非支配解集可以很清楚的看出各个目标之间的关系,从而更好地衡量各个目标,便于决策者选择具体的实施方案。
(2)单目标优化只能同时优化一个目标,而换热网络多目标综合可以使多个目标函数的结果收敛于Pareto前沿,实现同步优化多个目标函数。
3.2 展望
换热网络多目标综合是非常复杂的设计问题。模型的求解非常具有挑战性。虽然通过引入很多简化和假设可以采用传统多目标算法进行求解,但是与此同时也会导致优化结果严重偏离实际情况。未来的研究工作应在以下两方面得到重视。
(1)目前模型中考虑的约束和目标仍不全面,尽可能减少简化和假设,建立包括经济性、柔性、可靠性和环境影响度等在内的换热网络多目标综合模型。
(2)传统多目标算法越来越无法胜任复杂模型的求解,严重限制了换热网络多目标综合的发展,尝试性能更好的多目标进化算法(如NSGA-Ⅱ算法)是非常好的选择。
参 考 文 献
[1] 霍兆义,尹洪超,赵亮,等. 国内换热网络综合方法研究进展与展望[J]. 化工进展,2012,31(4):726-731.
[2] KANG L,LIU Y,LIANG X. Multi-objective optimization of heat exchanger networks based on analysis of minimum temperature difference and accumulated CO2emissions[J]. Applied Thermal Engineering,2015,87(5):736-748.
[3] RAVAGNANI M A S S,MANO T B,CARVALHO E P,et al. Multi-objective heat exchanger networks synthesis considering economic and environmental optimization[J]. Computer Aided Chemical Engineering,2014,33:1579-1584.
[4] YI D K,HAN Z Z,WANG K F,et al. Strategy for synthesis of flexible heat exchanger networks embedded with system reliability analysis[J]. Chinese Journal of Chemical Engineering,2013,21(7):742-753.
[5] ESCOBAR M,TRIERWEILER J O,GROSSMANN I E. Simultaneous synthesis of heat exchanger networks with operability considerations:flexibility and controllability[J]. Computers & Chemical Engineering,2013,55:158-180.
[6] WEN Y,SHONNARD D R. Environmental and economic assessments of heat exchanger networks for optimum minimum approach temperature[J]. Computers & Chemical Engineering,2003,27(11):1577-1590.
[7] CHEN C L,HUNG P S. Multicriteria synthesis of flexible heat-exchanger networks with uncertain source-stream temperatures[J]. Chemical Engineering and Processing:Process Intensification,2005,44(1):89-100.
[8] BJÖRK K M,WESTERLUND T. Proceedings of the IEASTED international conference:Modelling,identification,and control[C]// Acta Press,Calgary,AB,Canada,2002.
[9] SREEPATHI B K,RANGAIAH G P. Review of heat exchanger network retrofitting methodologies and their applications[J]. Industrial & Engineering Chemistry Research,2014,53(28):11205-11220.
[10] COELLO C A. Evolutionary multi-objective optimization:a historical view of the field[J]. Computational Intelligence Magazine,IEEE,2006,1(1):28-36.
[11] NA J,JUNG J,PARK C,et al. Simultaneous synthesis of a heat exchanger network with multiple utilities using utility substages[J]. Computers & Chemical Engineering,2015,79:70-79.
[12] ZHOU A,QU B Y,LI H,et al. Multiobjective evolutionary algorithms:a survey of the state of the art[J]. Swarm and Evolutionary Computation,2011,1(1):32-49.
[13] LÓPEZ-MALDONADO L A,PONCE-ORTEGA J M,SEGOVIA-HERNÁNDEZ J G. Multiobjective synthesis of heat exchanger networks minimizing the total annual cost and the environmental impact[J]. Applied Thermal Engineering,2011,31 (6):1099-1113.
[14] KLEMEŠ J J,KRAVANJA Z. Forty years of heat integration:pinch analysis and mathematical programming[J]. Current Opinion in Chemical Engineering,2013,2(4):461-474.
[15] 温录亮. 多目标最优化方法与应用[D]. 广州:暨南大学,2009.
[16] JIN Z L,CHEN X T,WANG Y Q,et al. Heat exchanger network synthesis based on environmental impact minimization[J]. Clean Technologies and Environmental Policy,2014,16(1):183-187. [17] KIRLIK G,SAYIN S. A new algorithm for generating all nondominated solutions of multiobjective discrete optimization problems[J]. European Journal of Operational Research,2014,232 (3):479-488.
[18] VASKAN P,GUILLÉN-GOSÁLBEZ G,JIMÉNEZ L. Multiobjective design of heat-exchanger networks considering several life cycle impacts using a rigorous MILP-based dimensionality reduction technique[J]. Applied Energy,2012,98:149-161.
[19] MIETTINEN K,MÄKELÄ M M. Interactive multiobjective optimization system WWW-NIMBUS on the internet[J]. Computers & Operations Research,2000,27(7):709-723.
[20] LAUKKANEN T,TVEIT T M,OJALEHTO V,et al. An interactive multi-objective approach to heat exchanger network synthesis[J]. Computers & Chemical Engineering,2010,34(6):943-952.
[21] LAUKKANEN T,TVEIT T M,OJALEHTO V,et al. Bilevel heat exchanger network synthesis with an interactive multi-objective optimization method[J]. Applied Thermal Engineering,2012,48:301-316.
[22] DEB K,PRATAP A,AGARWAL S,et al. A fast and elitist multi-objective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[23] METAXIOTIS K,LIAGKOURAS K. Multiobjective evolutionary algorithms for portfolio management:A comprehensive literature review[J]. Expert Systems with Applications,2012,39(14):11685-11698.
[24] 公茂果,焦李成,杨咚咚,等. 进化多目标优化算法研究[J]. 软件学报,2009,20(2):271-289.
[25] AGARWAL A,GUPTA S K. Multiobjective optimal design of heat exchanger networks using new adaptations of the elitist. nondominated sorting genetic algorithm,NSGA-Ⅱ[J]. Industrial & Engineering Chemistry Research,2008,47(10):3489-3501.
[26] 任建强. 管壳式换热器及换热器网络的多目标优化设计[D]. 济南:山东大学,2011.
[27] 林露. 基于非支配排序遗传算法的换热网络多目标优化[D]. 杭州:浙江工业大学,2013.
[28] SRINIVASAN S,RAMAKRISHNAN S. Evolutionary multi objective optimization for rule mining:a review[J]. Artificial Intelligence Review,2011,36(3):205-248.
[29] 高媛. 非支配排序遗传算法 (NSGA) 的研究与应用[D]. 杭州:浙江大学,2006.
[30] VON LÜCKEN C,BARÁN B,BRIZUELA C. A survey on multi-objective evolutionary algorithms for many-objective problems[J]. Computational Optimization and Applications,2014,58(3):707-756.
[31] 师瑞峰. 多目标进化算法研究及其在生产排序中的应用[D]. 北京:北京航空航天大学,2006.
[32] 马小姝,李宇龙,严浪. 传统多目标优化方法和多目标遗传算法的比较综述[J]. 电气传动自动化,2010,32(3):48-50.
综述与专论
Research progress on optimization algorithms in multi-objective synthesis of heat exchanger networks
LÜ Junfeng,XIAO Wu,WANG Kaifeng,LI Zhonghua,HE Gaohong
(State Key Laboratory of Fine Chemicals,R&D Center of Membrane Science and Technology,Dalian University of Technology,Dalian 116024,Liaoning,China)
Abstract:For the sustainable development in resources and energy,the designers should not only consider economy,but also flexibility,reliability,operability and environmental impact in the synthesis of heat exchanger networks(HENs). Multi-objective synthesis of HENs has got preliminary progress and drawn great attention. This paper illustrates the necessity of multi-objective synthesis of HENs and summarizes the research progress on multi-objective synthesis of HENs. The summary and comparison of the algorithms for solving multi-objective optimization problems were mainly focused. Application in multi-objective synthesis of HENs was reviewed. Research shows that traditional multi-objective algorithms are less suitable for solving the problems of complex superstructure. However,multi-objective evolutionary algorithms can solve multi-objective problems better in the synthesis of HENs. Non-dominated sorting genetic algorithm(NSGA-Ⅱ) is one of the most popular and effective applied algorithms. It was proposed that based on superstructure,establishing multi-objective models which involve economy,flexibility,reliability,operability and environmental impact and then present the decision makers with Pareto optimum solutions is the future of HEN synthesis.
Key words:systems engineering;optimal design;HENs;multi-objective;algorithms;NSGA-Ⅱ
基金项目:国家自然科学基金(21206014,21125628)、中央高校基本科研业务费专项基金(DUT14LAB14)及中国石油化工股份有限公司资助项目(X514001)。
收稿日期:2015-09-01;修改稿日期:2015-09-10。
DOI:10.16085/j.issn.1000-6613.2016.02.002
中图分类号:TQ 021.8
文献标志码:A
文章编号:1000–6613(2016)02–0352–06

