SI –FLAT板形仪工作特性仿真分析
Simulated analysis of the SI-FLAT contactless flatness measurement working characteristics
张 艺1,李洪波2,包仁人2
ZHANG Yi1, LI Hong-bo2, BAO Ren-ren2
(1.国家知识产权局专利局专利审查协作北京中心,北京 100190;2.北京科技大学 机械工程学院,北京 100083)
SI –FLAT板形仪工作特性仿真分析
Simulated analysis of the SI-FLAT contactless flatness measurement working characteristics
张艺1,李洪波2,包仁人2
ZHANG Yi1, LI Hong-bo2, BAO Ren-ren2
(1.国家知识产权局专利局专利审查协作北京中心,北京 100190;2.北京科技大学 机械工程学院,北京 100083)
摘 要:为掌握SI-FLAT板形仪的工作特性,以某2180mm冷连轧机配备的SI-FLAT非接触式板形仪为研究对象,分析了其基本测量原理。建立有限元仿真模型分析激振力沿带钢宽度方向的分布形式,发现当带钢宽度变化时,激振力在带钢宽度中间分布较为均匀,而在距边部250mm~300mm左右处开始出现较为明显的衰减。进一步建立带钢受迫振动过程仿真分析,分析表明带钢宽度方向中部振幅相对平缓,而在距边部250mm~300mm左右处开始出现较为明显的衰减,因此需在板形控制目标曲线中添加边部补偿量。
关键词:SI-FLAT板形仪;激振力;受迫振动;振幅;有限元
0 引言
板形是衡量冷轧带钢产品质量的一个重要方面,对冷轧带钢板形缺陷(残余应力)的检测是实现板形自动控制、消除板形缺陷的前提。冷轧板形在线自动检测技术可以分为接触式和非接触式两种,具有代表性的接触式自动检测技术为分割辊式张力检测技术,但其在检测过程中检测装置必须与带钢接触,从而容易磨损带钢表面;近年来,采用气流激振-涡流测幅原理的西门子SI-FLAT非接触式板形仪得到了比较普遍而成功的应用[1~3]。
国内某2180mm冷连轧机首次采用了SI-FLAT非接触式板形仪,与其他接触式板形仪相比,国内外关于SI-FLAT非接触式板形仪全面而深入的研究较少。文献[3~5]介绍了SI-FLAT非接触式板形仪的系统结构、工作原理与使用情况;文献[6]采用分条离散化的解析模型,将气动载荷简化为集中载荷,研究了带钢振幅-残余应力的关系等,采用有限元模型修正气动载荷分布规律,并与西门子公司提供的振幅-残余应力模型进行对比;文献[7]对SI-FLAT的测量准确性及误差分布形式进行了分析,解释了误差形成机理,同时给出了相应的补偿量计算方法;文献[2]在实际生产数据的基础上提出了气动载荷激振频率的设置原则,并利用有限元模型分析了具有几种典型残余应力分布形式的带钢在不同宽度、厚度、张应力等情况下固有频率对振幅的影响。
为进一步掌握SI-FLAT板形仪的工作特性,以某2180mm冷连轧机配备的SI-FLAT非接触式板形仪为研究对象,在对其基本测量原理进行分析的基础上,建立有限元仿真模型,对激振力横向分布规律以及带钢受迫振动过程进行仿真分析。
1 SI-FLAT非接触式板形仪检测原理
某2180mm冷连轧机配备的SI-FLAT非接触式板形仪主要包括以下四部分[3]:1)带有气孔和电涡流测距传感器的检测平台;2)用于产生低压的风机;3)空气管道;4)用于风机和调频器的传动控制设备。
SI-FLAT板形仪的主要检测装置是在带钢下方的非接触式电涡流传感器,通过一台风机将带钢与检测平台间的空气抽出,在带钢和检测平台间形成负压,利用空气通道中由变频电机控制转速的调频器改变负压大小,使带钢产生3Hz~10Hz的正弦型周期振荡。针对不同规格的带钢,通过调节风机转速使带钢的平均振幅保持在100µm~200µm的范围内。利用电涡流传感器测量出带钢在垂直方向的位置变化,通过快速傅里叶变换计算出带钢受迫振动的振幅,进而将带其代入板形计算模型求解带钢的横向延伸率分布。
2 激振力横向分布规律仿真分析
SI-FLAT板形仪通过气流对带钢施加的激振力沿带钢宽度方向并不是均匀分布的,尤其是在带钢边部,因边界条件的改变,激振力会出现明显区别于其他位置的变化,而这样的分布形式,必然会对带钢宽度方向各处振幅造成影响,给板形测量结果带来误差,因此必须确定激振力沿带钢宽度方向的分布形式,才能将测量误差定量化。
为分析激振力的分布形式,根据流场理论,利用有限元方法建立分析模型,首先对物理模型进行简化:
1)板形仪激振部分可视为由带钢与空气流体空间两部分组成,带钢可简化为流体中的壁面边界条件;
2)考虑带钢及SI-FLAT板形仪气流通道沿轧制中线对称,建立1/2模型;
3)气流通道可简化为长度与气流通道最大长度相同、面积与气孔总面积等同的矩形,经计算矩形宽度为15.73mm;
4)带钢上方空间只有接近带钢边部一定范围内的空气参与流场分析,带钢上方靠近中部的空气不纳入流体模型。
实际应用于2180mm冷连轧机SI-FLAT板形仪的风机额定流量为125m3/min,调频器设定频率为5.105Hz,带钢平均振幅约为150µm。带钢宽度B分别取1000mm、1500mm和2000mm,厚度取2mm,则空间流体区域的截面尺寸如图1所示,利用ANSYS Workbench建立如图2所示的几何模型,x为带钢宽度方向,z为带钢长度方向,取900mm,单元数量随带钢宽度不同而略有不同,约为90000个。利用Fluent软件进行仿真计算,湍流模型采用标准k-ε模型,考虑到空气流动速度较小,将空气设置为理想气体。将SI-FLAT板形仪测量平台的气流通道设置为流量出口边界,出口流量设置为额定流量的30%,气流通道所在平面的其他区域、带钢上表面及侧面设置为壁面边界,带钢上方及靠外一侧为压力入口边界设置大气压力,对称面设置为对称边界,各边界所在位置参考图2。
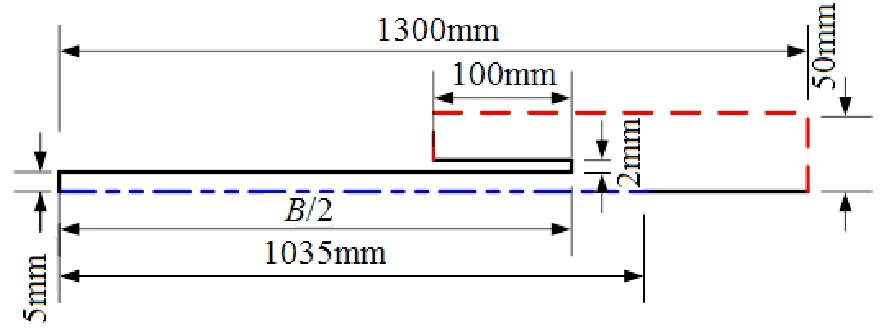
图1 仿真模型几何尺寸示意图

图2 激振气流半板宽仿真模型示意图
宽度为1500mm带钢下表面压力分布计算结果如图3所示。仅改变带钢宽度进行仿真计算,得到气流通道对称面带钢所受压力分布如图4所示,可见当带钢宽度变化时,激振力在带钢宽度中间分布较为均匀,而在距边部250mm~300mm左右处开始出现较为明显的衰减,这必然会对板形检测结果带来一定误差。

图3 宽度为1500mm带钢半板宽范围内受力分布仿真结果

图4 激振力沿带钢宽度分布
3 带钢受迫振动过程仿真分析
为进一步求取不均匀激振力对带钢振幅的影响还需建立激振力分布-振幅模型,此类问题的求解可采用解析法或有限元法,其中有限元法利用有限自由度的离散系统来代替无限自由度的连续系统,避开了数学上求解微分方程的困难,使得原来无法求解的问题有了数值解,且计算精度较高,是有效的工程分析手段。因此采用有限元法对带钢受迫振动进行分析。
冷轧出口处通常存在两个显著的特征:一是带钢受到大张力的作用,二是存在轧制方向的运动。相关研究[8]表明,运动速度对带钢固有频率的影响很小,可忽略不计,而张力对固有频率的影响较大,需予以考虑。SI-FLAT板形仪测量区域内带钢的长度和宽度均远大于厚度,符合薄板理论的假设,取带钢的中面为xy平面,z轴垂直于中面且与x轴、y轴形成右手螺旋,则板形检测过程可视为一对边简支、另一对边自由的矩形薄板在张力N(x)作用下的弹性矩形薄板受迫振动问题[9,10],如图5所示。
利用有限元软件ANSYS Mechanical APDL建立了带钢振动的仿真模型,模型单元采用弹性壳单元shell63,四节点六自由度,不考虑剪切变形。约束条件为沿轧制方向两端面简支,另两边自由,建立模型如图6所示。带钢y方向的长度对应板形检测段带钢长度取900mm,弹性模量2.1×1011Pa,泊松比0.3,密度7850kg/m3。生产过程中2180mm冷连轧机实际出口张力与带钢的截面积相关,二者之间近似呈线性关系,因此确定仿真模型主要参数如表1所示。

图5 板形检测段带钢受力示意图

图6 带钢受迫振动的有限元模型
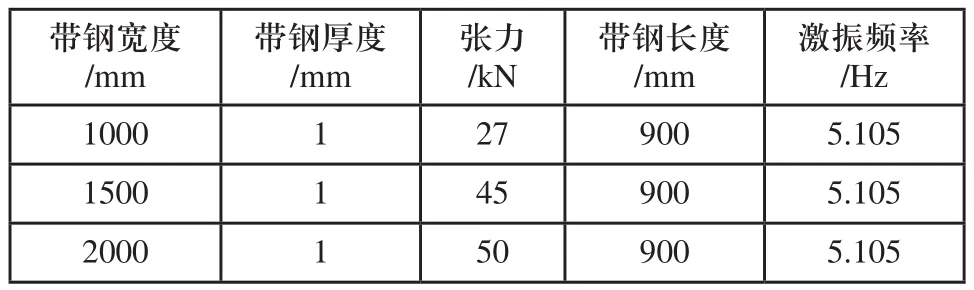
表1 带钢振动仿真模型主要参数
模态求解方法采用分块兰索斯法(B l o c k Lanczos),在计算一定范围内的固有频率时,该方法具有收敛速度快、计算精度高的特点。在进行带钢受迫振动的谐响应分析时,还需对带钢施加激振力,激振力的施加情况由前文激振力的仿真求解确定,本文采用的谐响应分析方法为模态叠加法。对应表1参数求解得到板形仪检测点处带钢振幅如图7所示。与激振力沿带钢宽度方向分布的情况类似,带钢宽度方向中部振幅相对平缓,而在距边部250mm~300mm左右处开始出现较为明显的衰减。这一衰减必然导致板形检测误差的存在,因此需要在板形控制系统中予以补偿,2180mm冷连轧机采用在目标曲线中添加边部补偿量的方法解决这一问题。
4 结论
1)SI-FLAT板形仪通过一台风机使带钢产生3Hz~10Hz的正弦型周期振荡,并利用电涡流传感器测量出带钢在垂直方向的位置变化,通过快速傅里叶变换计算出带钢受迫振动的振幅,根据板形计算模型求解带钢的横向延伸率分布。
2)有限元仿真分析表明,当带钢宽度变化时,激振力在带钢宽度中间分布较为均匀,而在距边部250mm~300mm左右处开始出现较为明显的衰减,这必然会对板形检测结果带来一定误差。
3)与激振力沿带钢宽度方向分布的情况类似,仿真分析表明带钢宽度方向中部振幅相对平缓,而在距边部250mm~300mm左右处开始出现较为明显的衰减,因此需在板形控制目标曲线中添加边部补偿量。

图7 振幅沿带钢宽度分布
参考文献:
[1] 赵小燕,张朝晖,迟健男,等.基于张力测量的板形检测技术[J].制造业自动化,2007,29(3):90-92.
[2] 杨光辉,张杰,曹建国,等.SI-FLAT板形仪激振频率设定[J].天津大学学报(自然科学与工程技术版),2014,47(10):871-878.
[3] 杨光辉,张杰,曹建国,等. 带钢非接触式平坦度检测原理及其检测系统[J]. 冶金自动化,2009(增1):665-668
[4] Spreitzhofer G,Duemmler A,Riess M, et al. SI-FLAT contactless flatness measurement for cold rolling mills and processing lines[J]. Revue de Metallurgie,2005,102(9):589-595.
[5] 秦政.新型冷轧带钢板型仪SI-FLAT在冷连轧机的应用[J].冶金自动化,2004(2):63-65.
[6] 黄桥宝.SI-FLAT冷轧带钢板形检测技术研究[D].北京:北京科技大学,2013.
[7] 包仁人.超宽冷连轧机带钢复杂板形的特征分析与控制[D].北京:北京科技大学,2015.
[8] 李健,颜云辉,郭星辉,等.基于薄板固有特性的连续热镀锌带钢表面质量在线控制[J].机械工程学报,2011,47(9):60-65.
[9] 张英世.两边受拉压的矩形薄板的振动[J].北京航空航天大学学报,1999,25(1):64-67.
[10] 杨桂芝,林长圣. 矩形薄板混合边界条件受迫振动分析[J].赤峰学院学报(自然科学版),2005,21(04):16-17.
作者简介:张艺(1983 -),女,四川乐山人,博士,主要工作内容为专利审察。
基金项目:中央高校基本科研业务费专项资金资助项目(FRF-TP-15-016A3)
收稿日期:2015-10-13
中图分类号:TG333.71
文献标识码:A
文章编号:1009-0134(2016)01-0016-03

