静电除尘用大功率高频高压电源预测控制研究
吴 尚,申兆丰,魏 月,曾庆军
(江苏科技大学 电子信息学院,江苏 镇江 212003)
静电除尘用大功率高频高压电源预测控制研究
吴尚,申兆丰,魏月,曾庆军
(江苏科技大学 电子信息学院,江苏 镇江212003)
摘要:静电除尘用大功率高频高压电源系统具有非线性、时变性、迟滞性等特点,需要一类数学模型要求低、自适应能力强的非线性控制方法;以自主研发的静电除尘用大功率高频高压电源为研究对象,基于现场实际电源系统试验结果,采用最小二乘法辨识系统的近似传递函数模型,最后设计了一种新颖的基于动态矩阵算法(DMC)的模型预测控制器,实现针对电源输出电压的控制;仿真结果表明,该算法具有稳定性好、自适应强等优点,并具有良好的控制效果。
关键词:静电除尘;高频高压电源;模型辨识;模型预测控制
0引言
随着大气污染问题越来越严重,国家对此十分重视,制定了相关法律、法规,来限制工业排放烟气中的粉尘浓度。常见的工业除尘方法有:机械除尘、洗涤除尘、过滤除尘和静电除尘等,静电除尘以其除尘效率高、范围广、维护方便、可处理高温气体等优点被广泛应用。目前静电除尘的供电电源主要是传统的工频电源,然而工频电源存在着体积庞大、材料浪费严重、电压输出波纹较大、电压侧谐波严重等问题。高频高压电源则以其体积小、重量轻、电损耗小、输出电压平滑、易于控制等优点[1-2],受到越来越多的关注。
目前,国内针对静电除尘高频电源控制方法的研究很多,例如文献[3]采用PID控制器控制晶闸管触发脉冲电路,调节输出电压大小,实现电压闭环控制;然而在实际使用中发现电源系统具有非线性、时变性及迟滞特性等特点,很难得到精准的数学模型,使得传统的PID控制器控制参数难以选定,因而控制往往失效。文献[4]采用了一种能使静电除尘系统稳定运行的模糊控制方法,在除尘器开机上电后,进入模糊控制阶段,在找到工作点并运行一段时间后,进入稳定运行阶段,达到除尘系统稳定运行的目的,实现自动控制效果。但是,这种模糊控制方法自适应能力不足,无法解决随着电源器件的老化、系统参数发生变化,而引起的控制器失配的情况。文献[5]提出了一种滑模变结构控制方法,通过该控制方法实现对电源系统的有效控制,并对参数变化及外部干扰具有很好的鲁棒性,但该方法难以克服抖振等缺点,易导致控制系统崩溃,并且该算法较复杂,工程实现困难。这就限制了上述控制方式的推广应用。
本文针对静电除尘用高频高压电源系统因非线性、时变性、迟滞性等原因造成的无法建立精确数学模型,以及工作环境复杂引起的外部干扰严重,超长时间运行过程中系统参数发生变化等问题,首先,依据自行研发的高频电源实际运行结果,结合该电源的实际系统模型,辨识出实际系统的控制模型,然后,利用该模型为预测模型,结合基于动态矩阵算法(DMC)的模型预测控制器,实现对电源的有效控制。该控制方法降低了对精确模型的依赖性,并对模型失配有很强的鲁棒性,控制系统实现简单,易于工程实现,克服了上述缺点。
1高频高压电源系统组成
静电除尘用高频高压电源系统分为主电路系统和控制系统两大部分,如图1所示。主电路系统主要由三相交流电源和除尘器等效网络之间依次连接的EMI滤波器、三相桥式整流模块、全桥逆变电路、谐振电容组、高匝比高频升压变压器、高压整流硅堆等组成。控制系统主要包括模拟信号采集单元、预测控制器、数字逻辑/驱动单元组成。
控制系统利用模拟信号采集单元采集主电路的二次电压信号,通过预测控制器计算、处理输出控制量,经过数字逻辑/驱动单元输出PWM驱动信号,控制绝缘栅双极型晶体管(IGBT),从而实现电源系统的控制。

图1 高频高压电源系统原理图
2高频高压电源数学模型
静电除尘电源系统为非线性、时变性、迟滞性系统,建立精确数学模型十分困难,并且即使建立较为精确的模型,也会因为模型过于复杂而无法直接使用。本文采用基波分析法,将系统中变量近似为正弦量,再利用线性交流分析法对系统进行分析,获得电源系统稳态情况下的传递函数模型。又由于系统建模时,环节众多以及多处近似,基波分析法获得的数学模型往往与实际系统相差甚远,所以,我们以该模型为基础,利用最小二乘法辨识系统传递函数参数,使获得的数学模型更贴近实际系统。
2.1电源系统传递函数
基波分析法是建立在系统所用器件均为理想器件、负载电容C0足够大等假设下的。由图1我们可知,系统电压输出实际为负载RLD两端电压,记为U0,对系统电压输出起控制作用的是系统数字逻辑/驱动单元输出的PWM信号,而PWM信号也是通过对IGBT的通断来影响图1中(A,B)点的电压输入(UAB)来实现控制的。所以我们可以认为UAB为系统的输入信号,U0为输出信号,建立的系统传递函数即为它们之间的传递函数。
首先,由基波分析法可得UAB与电容Cp两端电压UCp之间的等效交流电路[6],如图2。

图2 高频高压电源系统交流等效电路
其中:Ce,Re分别为等效电容和等效电阻。
然后可得UAB与电容Cp两端电压UCp之间的传递函数H(s):



其中:变压器副边对原边的匝比n、高频变压器极间电容Cp和漏感Ls、谐振电路串联电容Cs、负载电阻RLD、谐振频率fs为电路参数已知参量。
然后,我们根据高频变压器和单相全波整流器相关特性[7],可得UCp与U0之间的传递函数W(s):

最后,我们可得系统U0与UAB之间的传递函数G(s):
G(s)=H(s)·W(s)=
(1)
以上得到电源系统传递函数模型的近似结构,由于推导过程中多次近似,所以本文只参考此传递函数的结构形式,具体参数将采用最小二乘法辨识。
2.2模型辨识原理
本文讨论系统为单输入单输出系统,其离散系统[8]描述方程为:
z(k)=-a1z(k-1)-…-anaz(k-na)+b1u(k-1)+b2u(k-2)+…+bnau(k-nb)+e(k)
式中,z(k)为系统输出量的第k次观测值,u(k)为系统的第k次输入值,依此类推;e(k)是均值为零的随机噪声。
可得系统输入输出的最小二乘格式
z(k)=hT(k)θ+e(k)
式中,h为样本集合,θ为被辨识的参数集合。
取准则函数
(2)
式(2)表明,位置模型参数θ最可能的值是在实际观测值与计算值之累次误差的平方和达到最小值处,所得到的这种模型输出能最好地接近实际系统输出。
这样就利用最小二乘法得到了系统的离散模型,再将系统连续化得到系统传递函数。
2.4实际模型辨识
为使辨识出的模型更符合真实系统,在本文中,采用自主研发的静电除尘用大功率高频高压除尘电源在除尘现场实际输出的电压数据(如图3),与上文推导的数学模型相结合的方法,辨识系统的近似传递函数模型。本文使用的实际除尘电源运行方式,为固定频率、占空比下的电源系统直接运行方式,所以我们可以把这种运行模式下获得的数据看作系统的阶跃响应结果。
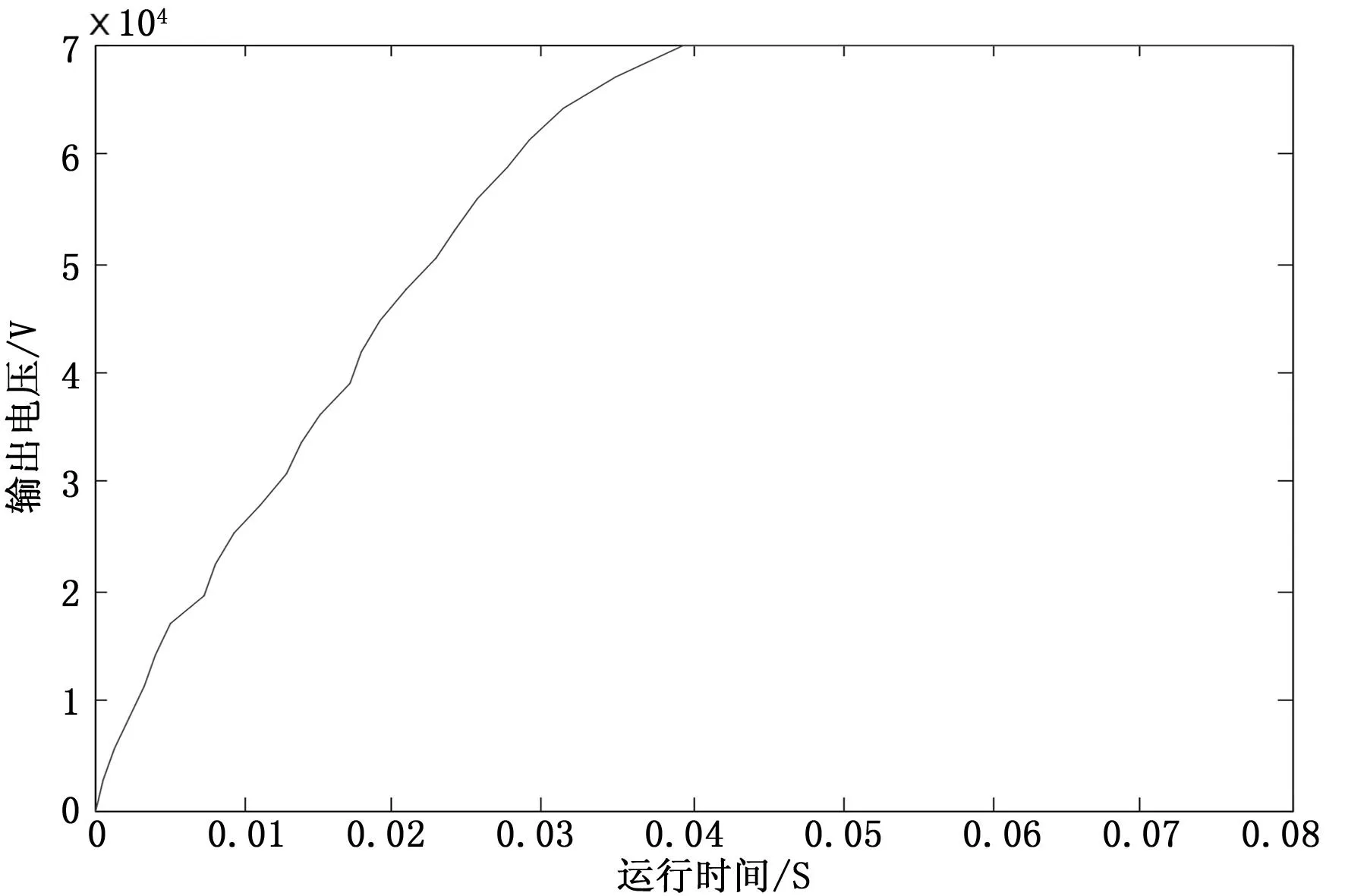
图3 高频高压电源实际输出波形
依据高频高压电源除尘现场实际输出电压值,采用最小二乘法辨识出系统的传递函数模型:
(3)
3动态矩阵算法(DMC)的状态空间实现
为了充分利用现代控制(特别是最优控制)的理论成果,本文采用DMC算法的状态空间实现方法,进行控制研究,由文献[9]可知所建立的状态空间阶跃响应模型,与传统的卷积表达形式是一致的。
首先,将被控系统传递函数模型转变为状态空间方程,并求得其单位阶跃响应模型,形式如下:
(4)


由式(4)设计状态观测器,
(5)
其中:KF是估计器增益。
设定预测时域为p,控制时域为m,且m≤p,控制时域之外,控制量不变,有预测方程:
(6)
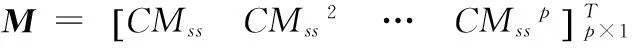

系统性能指标满足以下条件:

(7)
其中:Γy,Γu为加权矩阵,R(k+1)为参考序列。
将式(6)带入式(7)后,得
(8)
经推导得DMC控制律:
(9)
其中:Kmpc为控制增益,
将式(8)带入式(9)后,得
控制量为:
u(k)=u(k-1)+Δu(k-1)
(10)
数字逻辑/驱动单元利用输出的控制量来确定PWM信号,完成系统控制。
4高频高压电源仿真实验
4.1高频高压电源PID算法仿真实验
利用传递函数(3)为预测模型,建立针对高频电源模型预测控制系统,并进行实验,为了显示模型预测控制的效果,本文采用PID控制为对照组。
PID控制器仿真模型结果见图4,横坐标为系统运行时间,纵坐标为电源系统二次电压输出。
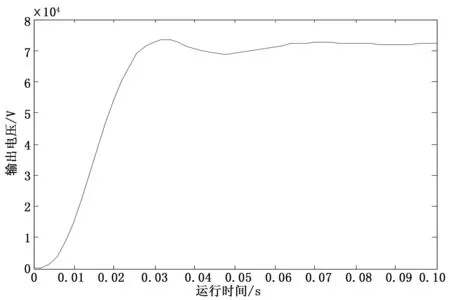
图4 PID控制器仿真结果
4.2高频高压电源DMC算法仿真实验
DMC控制器实验结果见图5,图中上方的图是电源系统二次电压输出仿真结果,下方的图为电源模型预测控制系统的输出坐标图,即式(10)的控制量输出,此控制量经过数字逻辑/驱动单元转变为PWM信号,实现针对系统的控制。
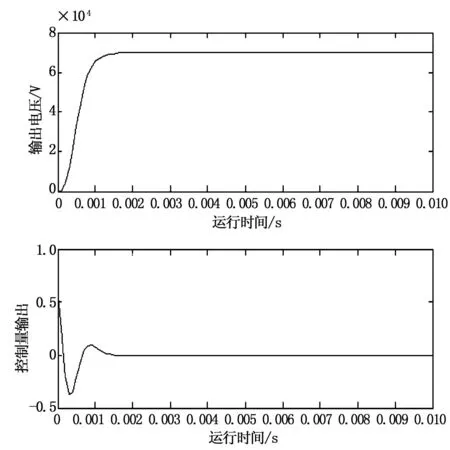
图5 预测控制器仿真结果
4.3模型失配情况下的DMC控制
在实际电源系统中,随着设备的使用以及外界复杂环境的影响,设备参数会出现变化,这时就要求控制器针对模型失配的鲁棒性要强,本文依照现场运行经验,设定电源系统数学模型参数均增加20%,并且出现时延工况,得到如式(11)所示模型,其仿真结果与未失配情况下的仿真结果如图6所示。
(11)


图6模型未失配、失配情况下的预测控制器仿真结果
4.4仿真结果分析
通过对比图3、图4可知,应用PID控制方法对电源系统进行控制时,系统快速性比开环系统略好,但面对结构较为复杂,传递函数阶次较高的高频电源系统时,参数难以确定,控制效果不够理想。然而,再次对比图5可知,预测控制器仿真结果良好,相比开环系统、PID控制系统性能提升明显,预测控制器控制的电源系统调节时间短,并且电压输出稳定,无抖振等不良现象发生,效果远优于开环系统和PID控制器系统,系统的仿真输出快速性、稳定性都达到了理想效果。
通过图7可知,基于动态矩阵算法(DMC)的模型预测控制系统,在出现模型失配情况下,虽然开始时快速性下降,但能很快进入稳定状态,控制输出仍然符合期望,效果依然良好,说明该控制方法具有良好的鲁棒性。
5结论
本文以静电除尘用高频高压电源为研究对象,介绍了电源系统组成,以基波分析法分析了电源系统,并得到了近似传递函数模型,同时,结合电源系统实际输出,依据最小二乘法辨识出电源系统传递函数模型的具体参数,建立了电源系统的近似模型。设计了状态空间函数模型实现的、以动态矩阵算法为核心的模型预测控制器,并设计仿真实验,经过多次调试,得到了较好的控制效果,证明了预测控制器的可行性,并与PID控制器仿真结果对比,证明了该预测控制器的优越性,最后,验证了模型失配情况下控制器的有效性,证明该控制器具有良好的鲁棒性。该控制系统实现简单,易于工程上实现。
参考文献:
[1]Thiago B S,Muhlethaler J,Linner J,et al.Automated design of a high power high frequency LCC resonant converter for electrostatic precipitator[J].IEEE Transactions on Industrial Electronics,2013,60(11):4805-4819.
[2]李洪文,李元春.经纬仪伺服系统功率开关电源及控制系统设计[J].计算机测量与控制, 2006,14(1):78-81.
[3]郭勇.基于DSP的高压直流静电除尘电源控制系统[J].电工技术,2007(10).
[4]杨炜,曾庆军,陈峰.模糊控制在静电除尘高频高压电源中的应用研究[J].电子设计工程,2014(2).
[5]Castilla M,Vicuna L G,Guerrero J M,et al.Sliding-mode control of quantum series-parallel resonant converters via input-output Linearization[J].IEEE Transactions on Industrial Electronics, 2005,50(2).
[6]夏冰.LCC谐振变换器在大功率高输出电压场合的应用研究[D].南京:南京航空航天大学,2008.
[7]由克伟.可控硅整流器的数学模型[J].成都科技大学学报,1979(2).
[8]任晓军,李四保,谢劲松.基于Matlab的电动舵系统模型辨识[J].战术导弹控制技术,2010,27(3).
[9]陈虹.模型预测控制[M].北京:科学出版社,2013.
Research on Prediction Control of High-power High-frequency High-voltage Power for Electrostatic Precipitator
Wu Shang,Shen Zhaofeng,Wei Yue,Zeng Qingjun
(School of Electronics and Information, Jiangsu University of Science and Technology, Zhenjiang212003, China)
Abstract:The dust movement by high-power high-frequency high-voltage power is characterized with nonlinear, time-varying, hysteresis and so forth. Thus, it requires a nonlinear control algorithm which has better adaptive features and a low demand for mathematical models. A high-power high-frequency high-voltage power,which is independently developed for electrostatic precipitator, is selected as the research object. Based on the field experiment results, parameters of the approximate transfer function are indentified by using least aquare method. A new Model Predictive Controller based on dynamic matrix control algorithm (DMC) is designed, realizing the control for the output voltage of power. Simulation results present that this algorithm has such advantages as good stability and strong self-adapting, with great control effects as a whole.
Keywords:electrostatic precipitator; high-frequency high-voltage power; model identification; model predictive control
文章编号:1671-4598(2016)02-0107-04
DOI:10.16526/j.cnki.11-4762/tp.2016.02.029
中图分类号:TP242
文献标识码:A
作者简介:吴尚(1988-),男,江苏徐州市人,硕士研究生,主要从事智能电气与系统、现代综合测控技术方向的研究。曾庆军(1969-),男,江苏句容人,博士,教授,主要从事先进控制理论与应用、现代测控与智能系统方向的研究。
基金项目:江苏省科技支撑计划项目(BE2012146)。
收稿日期:2015-09-01;修回日期:2015-09-24。

