基于连续函数的条件选择算法的监考安排研究

徐苏秦　张　盛　公安海警学院　315000



基于连续函数的条件选择算法的监考安排研究

徐苏秦张盛公安海警学院315000

现有高校监考管理系统在公平度方面仍存在问题，如教师年龄、性别、职称等因素对应的权值突变性导致公平度曲线不连续。提出一种基于连续函数的条件选择算法进一步提高监考管理系统的公平性。该算法结合随机选择和基于平滑曲线的权值计算，综合考虑了人性化因素和职称、年龄等客观因素。分析表明该方案的公平度比现有方案更合理。

【关键词】

软件算法；监考管理系统；条件选择；公平度计算

1　研究背景

现如今，虽然国内外关于监考安排的研究已有很多，但自动排监考系统的实际应用还没有广泛推广，同时算法的兼容性较低。Carter 等（1996）最早提出此问题，并设计了一个EXAMINE系统，采用序列建构方法寻找最优解。Casey 和 Thompson（2003）结合排序和退火算法分配教师资源。国内张恒等（2012）提出了基于 Access 数据库查询操作的优先级算法，但仍需人工进行安排。上述算法的研究并没有对教师自身条件进行人性化权值约束，没有综合实际条件进行方案优化。王菊雅等（2015）基于自动排监考算法研究中，提出了监考教师能力特征值的方法，综合考虑教师自身因素，通过计算能力特征值进行优化组合。但仍存在缺陷，如年龄系数存在突变、岗位系数过于笼统。同时，算法直接进行硬性条件限制，会产生“特权现象”，造成安排的不公平性。

基于连续函数的条件选择算法，首先通过随机数产生器随机选取部分监考候选人，大大削弱硬性特权制约，做到绝对公平，同时又人性化将监考教师的各因素约束权值运用连续函数进行确定，根据公平度函数得到该教师的监考能力值，进一步优化监考分配方案。

2　基于连续函数的条件选择算法

条件选择算法，将教师约束条件按性质不同分为一般条件和特殊条件。一般条件是每位教师均要考虑的因素，如年龄、职称、性别等；特殊条件是教师个人因素，如出差、开会、生病请假等。

2.1公平度函数的构建

式中：ρw为水的密度，kg/m3；vi为断面流速，m/s；xi、xj为距离，m；ρ为压力，N；fi为质量力，m/s2；v为流体运动的黏滞系数。

公平度函数根据上述条件选择分别引入加性参数和乘性参数。将一般条件的影响因素列为加性参数，将特殊条件的影响因素列为乘性参数。

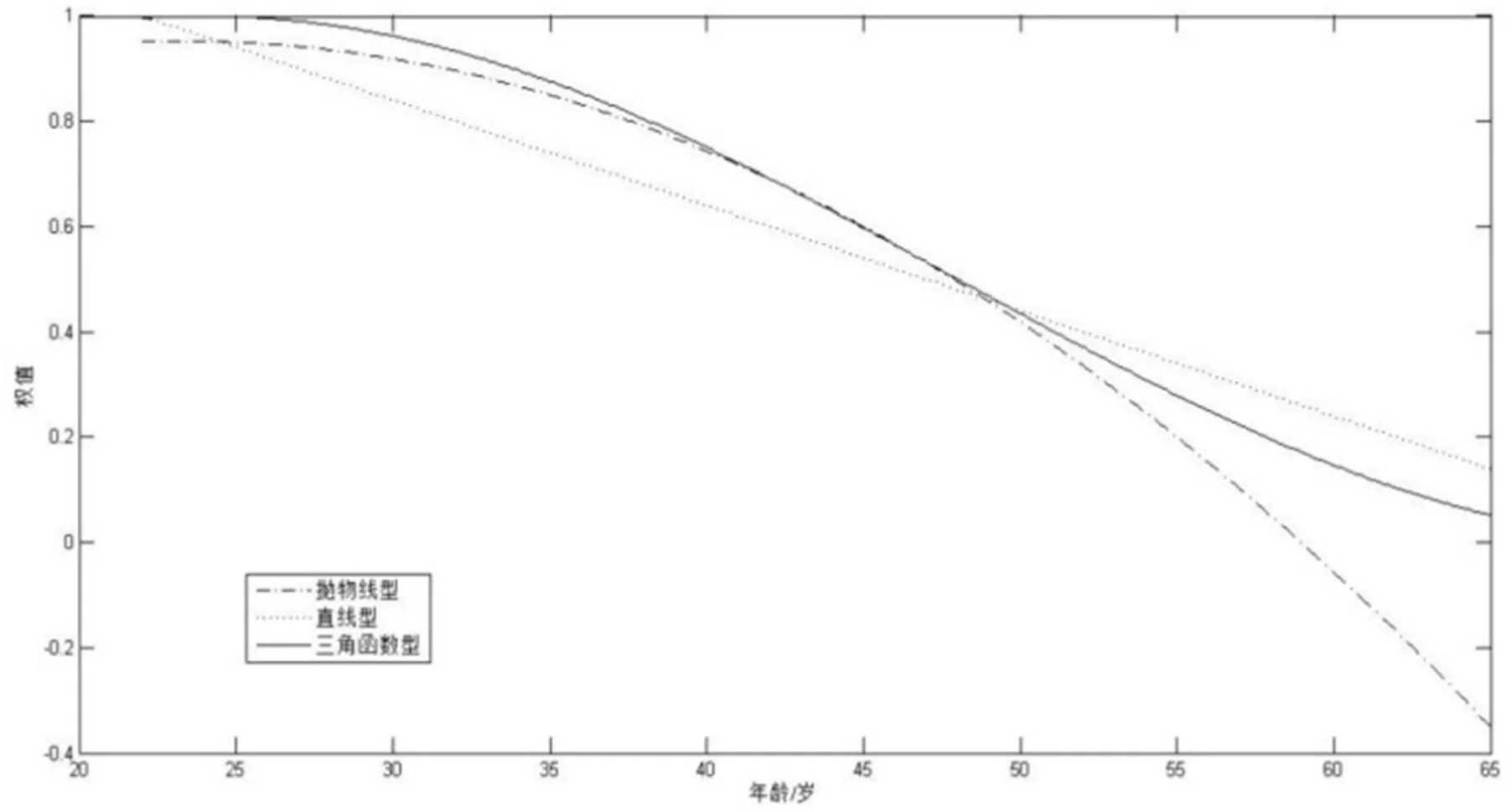
图2年龄权值比较图

2.1.1加性参数

在一般条件中，分别对监考教师的年龄、性别、职称等因素构建相应连续函数进行监考能力值约束，将各因素权值进行累加。

（1）年龄

在自动排监考算法中，通过设定年龄界限值MA，大于MA教师年龄系数A=0.1，其他A=1.此算法存在权值在临界点MA的突变性。为解决这一问题，通过构建连续函数A=f(x)来平滑权值曲线。f(x)函数类型选取原则根据实际需求选取，以下通过构建两种典型函数进行分析。

①直线型。适用于年龄结构分布比较均衡的情况，权值随年龄线性变化，实现了绝对公平。系统以A(x)=kx+b进行表示，其中，x为教师年龄，A为年龄权值，k,b系数可灵活设定。若某校教师年龄在22—65岁之间，令系数变化范围在0.1-1间，则

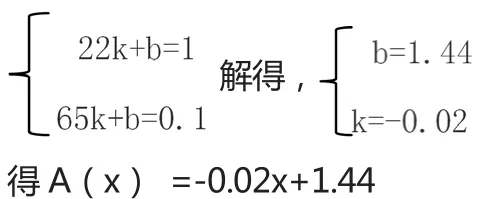
②曲线型。适用于年龄分布不均的情况，可根据实际需求（如照顾年龄结构偏老群体）选择相应函数，如三角函数、二次函数、三次函数等。系统以正弦函数A(x)=BsinCx+D进行表示，其中，x为教师年龄，A为年龄的权值，B,C,D系数可灵活设定。若同上条件，得，A（x）=1/2（sin（(π/48）)x+1）

（2）性别：系统以S进行表示，男教师S=p,女教师S=q。p，q根据学院实际男女教师比重或照顾政策灵活自定义。

（3）职称：通过细化职称，构建分段函

数进行权值计算。系统以Z(z)=i进行表示，其中，z为职称种类，可分为教授、副教授、讲师、助教等， i可根据职务繁忙度灵活定义。

2.1.2乘性参数

在特殊条件中，特殊因子y的值随特殊情况变化而确定。如表1分析，将特殊因子y作为乘性参数决定监考最终值。

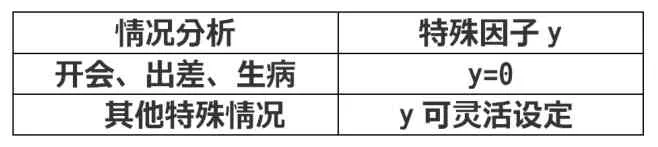
表1　乘性参数的设置

2.2公平度计算

定义公平度函数w(x,y,z,S)= （A(x)+S+Z(z)）*y。通过加性参数和乘性参数相结合进行运算，优化了算法的合理性。监考可能值P=1/n*w，其中，n为教师数量，每位教师在完全等概监考条件下加以权值w限定，得到最终监考可能值。

2.3算法步骤

步骤一：随机数产生器随机产生一部分教师（可设定具体比例）作为监考候选人；

步骤二：综合教师因素约束，根据公平度函数计算出每位候选人监考可能值；

步骤三：进行降序排序；

步骤四：根据所需监考教师人数n，选取排名前n名教师。

需要指出的是，监考候选人数一定要大于所需监考人数，可参照差额选举办法设定一定比例，如120%。

3　算法的比较与分析

在自动排监考算法中,年龄系数A在临界点MA存在权值突变现象，如图1所示。在条件选择算法的优化下， A能随年龄x变化而变化，同时，构建不同类型函数可满足不同需求。图2曲线对比图中明显看出，构建连续函数得到的年龄权值解决了临界点突变问题。同时，抛物线型和三角函数型变化趋势由慢变快，充分照顾了偏老结构的教师群体。

在教师其他因素均相同的情况下，通过控制年龄的变化，观察年龄权值的变化。以下选取部分年龄进行数据分析：

由表2中可看出，通过构建连续函数解决了在同等条件下由于系数的单一化，而无法确定监考教师的漏洞，如45岁和65岁的教师，由于年龄系数值相同而无法选择谁去监考。同时，由ΔA值看出，在构建不同连续函数中，尤其曲线型函数考虑了年龄结构偏大的教师，年龄越大，ΔA值越大变化越陡，即权值越低。

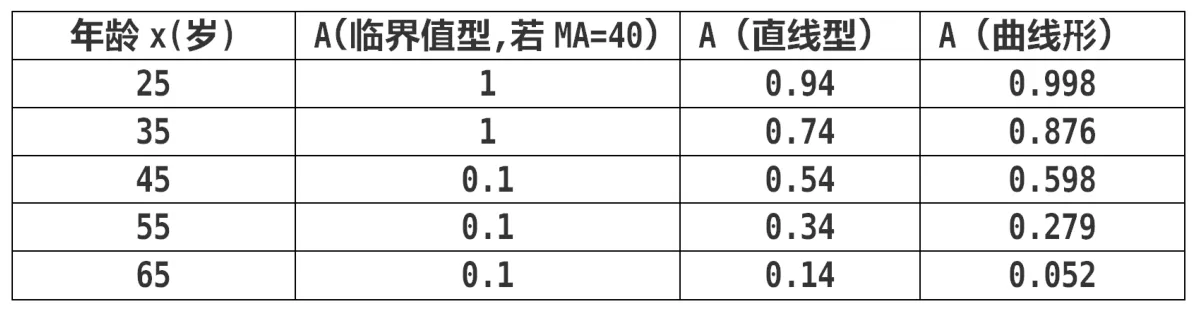
表2　年龄权值数据表

以上着重分析了不同算法中年龄权值的变化特点，同理也可分析，性别和职称通过连续函数确定权值更加公平化和人性化。

4　结语

本文提出基于连续函数的条件选择算法，在随机选取监考候选人的基础上通过构建各因素的连续函数进行权值约束，充分体现了公平原则下的“以人为本”教学管理理念，最大优化监考安排。此算法不仅能应用于监考安排中，同样适用于各单位公差勤务安排等。

【参考文献】

[1］Carter M W，Laporte G，Lee S Y.Examination timetabling：Algorithmic strategies and application ［J］.The Journal of theOperational Research Society，1996，47（03）：373-383.

［2］Casey S，Thompson J.Grasping the examination scheduling problem［R］. Practice and Theoryof Automated Timetabling IV，Springer Berlin Heidelberg，2003：232-244.

［3］张 恒，卢亚玲，温红艳.高校监考安排管理系统的研究［J］.科技信息，2013（34）：85-86.

[4]王菊雅，刘海霞，陈淑玉.基于自动排监考算法的监考信息管理系统的研究与设计.《工业控制计算机》2015 年第28 卷第4 期：135-136.