基于离散分数阶Fourier变换本征矢量分解的图像加密算法

田 玉 萍

(黑河学院数学系　黑龙江 黑河 164300)



基于离散分数阶Fourier变换本征矢量分解的图像加密算法

田 玉 萍

(黑河学院数学系黑龙江 黑河 164300)

摘要针对目前采用分数阶傅里叶变换对图像进行加密的算法中，其主要存在密钥敏感性较差等不足，提出一种将离散分数阶Fourier变换与指数随机相位掩膜、Logistic混沌映射结合起来进行加密的新算法。该算法在加密过程采用离散分数阶Fourier变换本征矢量分解的方法进行运算，显著提高了加密系统的安全性能。首先，对原始图像进行Logistic映射混沌置乱处理，接着与第一个指数随机矩阵A相乘，之后再经α阶离散的分数阶Fourier变换；其次，与第二个指数随机矩阵B相乘,再经β阶离散的分数阶Fourier变换；最后，利用Logistic映射对图像再次进行置乱处理来获得最终的密文图像。仿真结果表明：与其他类似加密机制相比，该加密系统兼顾了更强的密钥敏感性以及更高的安全性。

关键词图像加密离散分数阶Fourier变换本征矢量分解密钥敏感性混沌置乱

IMAGE ENCRYPTION ALGORITHM BASED ON EIGENVECTOR DECOMPOSITION OF DISCRETE FRACTIONAL FOURIER TRANSFORM

Tian Yuping

(Department of Mathematics,Heihe College,Heihe 164300,Heilongjiang,China)

AbstractCurrent algorithms use discrete fractional Fourier transform (DFRFT) to encrypt images, they have the shortcoming of poor sensitivity in key. In light of this, we proposed a new algorithm, which combines the discrete fractional Fourier transform with exponential random phase mask and Logistic chaotic mapping for encryption. In encryption process the algorithm adopts the method of discrete fractional Fourier transform eigenvector decomposition for computing, and this significantly improves the safety performance of the encryption system. First, it conducts Logistic mapping chaotic scrambling processing on original image, then is multiplied by the first exponential random matrix A, after that the DFRFT of order α is applied; Secondly, it is multiplied by the second exponential random matrix B, then the DFRFT of order β is applied again; Finally, it uses Logistic mapping to scramble the image once again to get the final ciphertext image. Simulation results showed that compared with other similar encryption mechanisms, the proposed encryption system considered both the stronger key sensitivity and higher security.

KeywordsImage encryptionDiscrete fractional Fourier transformEigenvector decompositionKey sensitivityChaotic scrambling

0引言

随着计算机网络以及多媒体技术的快速发展，数字图像不仅涉及了个人隐私的安全性，而且也涉及了国家信息保密的安全性，其在传输过程中容易遭受非法攻击和泄露，因此数字图像信息安全已经成为了当今时代具有重要现实意义的研究课题，图像加密技术也越来越受到人们密切的关注与重视[1-4]。

分数阶Fourier变换[5,6]是一种与具有交叉项干扰的二次型时频分布有显著差异的新型时频分析工具。它已经在信息安全领域、目标检测领域以及信号处理领域等均显示出了极为优良的应用价值，已经逐渐成为图像加密中的重要研究热点之一[7,8]。何俊发[9]等人利用分数傅里叶变换的正变换和逆变换来完成图像的加密变换，实验结果表明该加密方案具有可行性，并且也一定程度上提高了图像的安全性；但是，该方案也存在某些弊端，例如只有在正、逆变换级次相同或满足周期条件这两种情况下，才能正确解密出原始图像，并且该算法的安全性还不够高。崔得龙[10]等人对分数阶傅里叶变换的加密算法进行了改进，提出了一种同时结合随机相位掩膜、混沌系统的新算法，实验结果证明了该算法的安全性能较高。王雅庆[11]等人提出了一种将分数阶Fourier变换和混沌系统结合在一块的数字图像加密算法，方案首先利用混沌将图像进行置乱处理，然后再执行X方向和Y方向的离散分数阶Fourier变换，实验结果表明，加密算法的安全性很好。

上述基于分数阶傅里叶变换的相关加密算法，虽然可以在一定程度上提高加密系统的安全性，但是还存在一些不足，如系统的密钥空间较小，导致抗穷举攻击性能较差；密文图像对密钥的敏感性还相对较差等。对此，本文为了进一步提高加密系统的密钥敏感性及安全性，提出一种基于离散分数阶Fourier变换本征矢量分解结合指数随机相位掩膜的新加密算法；最后测试了本文算法的安全性能。

1分数阶Fourier变换理论

对于信号x(t)的分数阶Fourier变换，其定义[6]如下：

(1)

其中，核函数Kp(u,t)可表示为：

(2)

(3)

其中，式中的k≥0,m≤M-1。矩阵X中只有四个本征值，它们分别是1，-1，j以及-j。引入另外一个M×M矩阵Y,其定义如下：

(4)

Ym,m+1=Ym+1,m=10≤n≤M-2

(5)

YM-1,0=Y0,m-1=1

(6)

当YZ=ZY时，它们之间可以相互交换，并且有相同的本征矢量值，但是它们的本征值却不同。因此，对于一个M×M离散的分数阶Fourier变换，可以应用离散Fourier变换Hermite本征矢量来构造离散的分数阶Fourier变换的本征矢量，其变换算子[11]可以表示为：

(7)

式中，M是离散信号的有效长度；v是由离散Fourier变换Hermite本征矢量构造出来的酉矩阵；vk是离散Fourier变换的第k个Hermite本征矢量；D为对角矩阵；T为转置矩阵。而矩阵V则可以表示为如下形式：

(8)

2本文加密算法设计

本文采用离散分数阶Fourier变换结合双随机相位矩阵对图像进行加密。首先原始图像p经Logistic映射进行图像像素值置乱处理，将处理后得到的图像与第一个指数随机矩阵A相乘，之后再经α阶离散的分数阶Fourier变换，得到处理后的图像p′；接着，将处理后的图像p′与第二个指数随机矩阵B相乘,再经β阶离散的分数阶Fourier变换,获得加密图像p″，最后利用Logistic映射对图像再次进行置乱处理，获得最终的密文图像。加密过程的流程设计如图1所示。

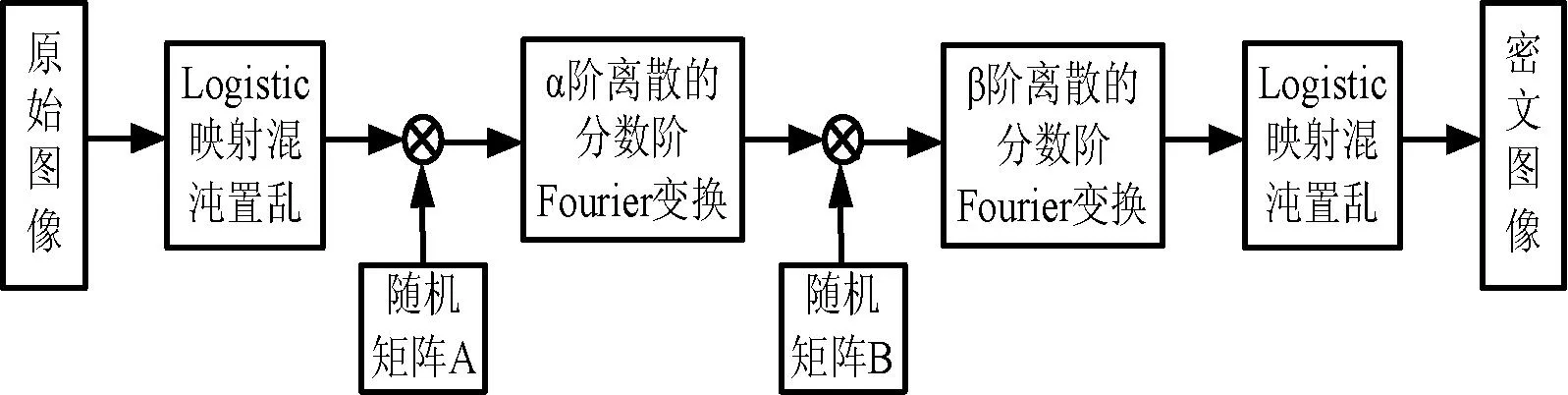
图1　本文提出的加密流程图

2.1图像加密过程设计

(1) 原始图像。本文加密的图像是大小为M×N的灰度图像，其中，M为图像像素总行数，N为图像像素总列数；

(2) Logistic映射混沌置乱。设置初始值X0和控制参数u0，代入Logistic映射方程Xn+1=uXn(1-Xn)(3.5669≤μ≤4，0≤X0≤1)，迭代N次，生成长度为M×N的混沌序列L，接着对混沌序列L进行排序来获得新的序列L′;将原始图像的像素值按先后顺序转换成长度为M×N的一维序列X, 然后利用L′来对X进行置乱处理。置乱处理方式如下：

X′(L′(i))=X(i)i=1,2,…,M×N

(9)

(3) 矩阵A变换。将经Logistic映射处理后的图像P与指数随机矩阵A相乘,矩阵A=ejφn。其运算公式如下：

H′=P⊗A=P⊗ejφn(x,y)

(10)

(4) α阶离散分数阶Fourier变换。将已经完成了步骤(3)处理后的图像经α阶离散分数阶Fourier变换，运算公式如下：

H″=Xα(P⊗ejφn(x,y))

(11)

(5) 矩阵B变换。将步骤(4)得到的图像与指数随机矩阵B相乘,矩阵B=ejβm(其中，矩阵B与矩阵A相互独立)。运算公式如下：

H‴=(Xα(P×ejφn(x,y)))×ejβm(x,y)

(12)

(6) β阶离散分数阶Fourier变换 将已经完成了步骤(5)处理后的图像经β阶离散分数阶Fourier变换，运算公式如下：

W=Xβ((Xα(P×ejφn(x,y)))×ejβm(x,y)

(13)

(14)

其中，式中的t(x,y)表示为置乱矩阵T(x,y)的元素值。

2.2图像解密过程设计

图像的解密过程是加密过程的逆过程，具体的解密流程如图2所示。

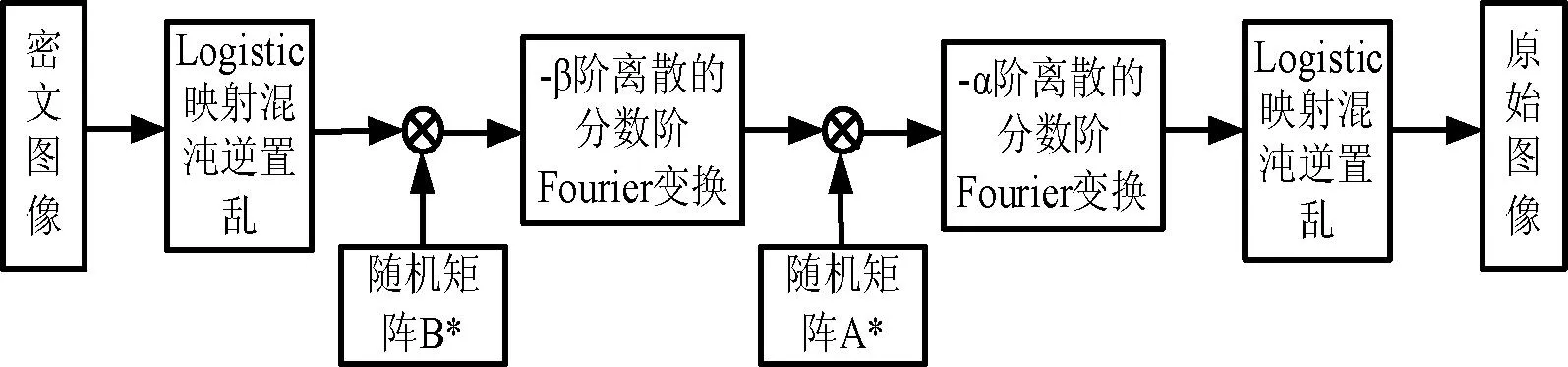
图2　本文提出的解密流程图

解密过程大致描述如下：

(1) 利用Logistic映射置乱矩阵T对密文图像进行反置乱处理；

(2) 将反置乱后的图像经-β阶离散分数阶Fourier变换，运算公式为：

W′=X-β(W)=X-β(Xβ(Xα(P⊗ejφn(x,y)⊗ejβm(x,y))

(15)

(3) 将W′与指数随机矩阵B*=e-jβm(x,y)相乘，得到W″：

W″=(X-β(Xβ((Xα(P⊗ejφn(x,y)))⊗ejβm(x,y))))⊗e-jβm(x,y)

(16)

(4) 将W″经-α阶离散分数阶Fourier变换，得到W‴：

W‴=X-α((X-β(Xβ((Xα(P⊗ejφn(x,y)))⊗

ejβm(x,y))))⊗e-jβm(x,y)

(17)

(5) 将W‴与指数随机矩阵A*=e-jαn(x,y)相乘：

S=(X-α((X-β(Xβ((Xα(P⊗ejφn(x,y)))⊗

ejβm(x,y))))⊗e-jβm(x,y)))⊗e-jφn(x,y)

(18)

(6) 对S再次进行Logistic映射反置乱处理，最终获得原始图像。

3仿真结果及分析

本文将文献[10](记作A算法)和文献[11](记作B算法)作为对照组来测试本文加密算法的安全性能，仿真图像是一个大小为256×256的灰度图像，在MATLAB7.1软件平台下进行仿真实验。仿真条件为：Intel 2.5 GHz，双核CPU，16 GB的内存，运行系统Windows 7。

3.1图像加密效果对比分析

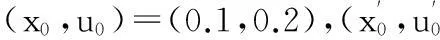
图3　图像加密算法结果

为了进一步量化不同加密算法的安全性，本文引用信息熵来评估[12,13]：

(19)

其中，L为像素值，p(mi)为mi出现的概率。

经不同加密算法处理后密文的信息熵结果见表1。从表1中可以看出，利用本加密算法处理后的密文熵值均比A、B加密算法的熵值要更大。这表明本文加密算法的抗熵攻击性及安全性均更好。

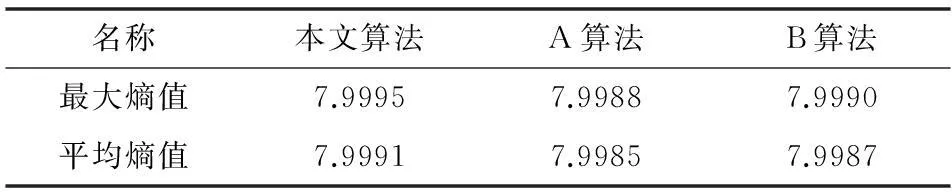
表1　不同加密算法处理后密文的信息熵值

3.2图像统计特征分析

本文通过比较加密前后图像灰度直方图的分布特点来进一步分析系统的抵御统计攻击性能，分析结果如图4所示。由图4(a)可知，初始图像像素点的分布呈现出不均匀态势，直方图波动程度较大，很容易受到攻击，其安全性较低。而经本文算法加密后的密文图像，直方图发生了很大的改变，如图4(d)所示，其像素分布比较均匀，表明本文采用的加密算法具有特别好的加密效果，安全性高；然而，A、B算法的密文直方图却呈现不均分布的特征，如图4(b)和4(c)所示，密文直方图波动程度较图4(d)的大，说明它们的随机性以及冗余性较低，与本文算法的安全性相比，均更容易受到攻击。

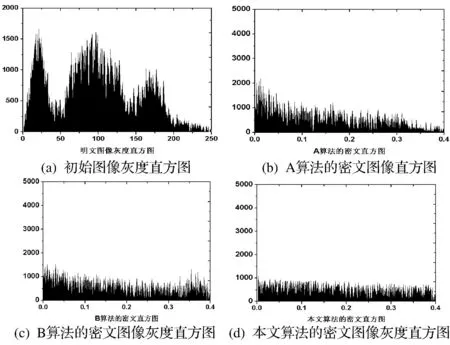
图4　灰度直方图仿真结果

3.3密钥空间对比分析

3.4密钥敏感性分析

密钥敏感性越强，则说明加密算法抵抗差分攻击性能也越强。本文测试参数x1(0)的敏感性。在其他参数不变的情况下，将x1(0)增加或减去一个极其微小干扰值δ后，变为(x0+δ)。图5为当δ取10-14时的密钥敏感性能仿真测试结果，图5(a)为正确密钥对应的密文；图5(b)为(x0+δ)密钥对应的密文。从图中可以看到，当加密密钥发生极其微小变化时，二者的像素点差异分布为对角形式，表明所得到的密文是截然不同的，见图5(c)。图5(d)更加直观体现了本文算法的密钥敏感性，当x1(0)发生极其微小变动时，其MSE曲线波动剧烈。变换阶数偏差MSE曲线如图5(e)所示。 从图5(e)中可以看出，当加密过程中的单个阶数密钥误差达到或超过0.01时，其MSE曲线呈现尖锐上升趋势，并且相对于其他两种加密算法，本加密算法的趋势更明显。这说明本文加密算法的密钥敏感性较强，且满足严格的“雪崩准则”。

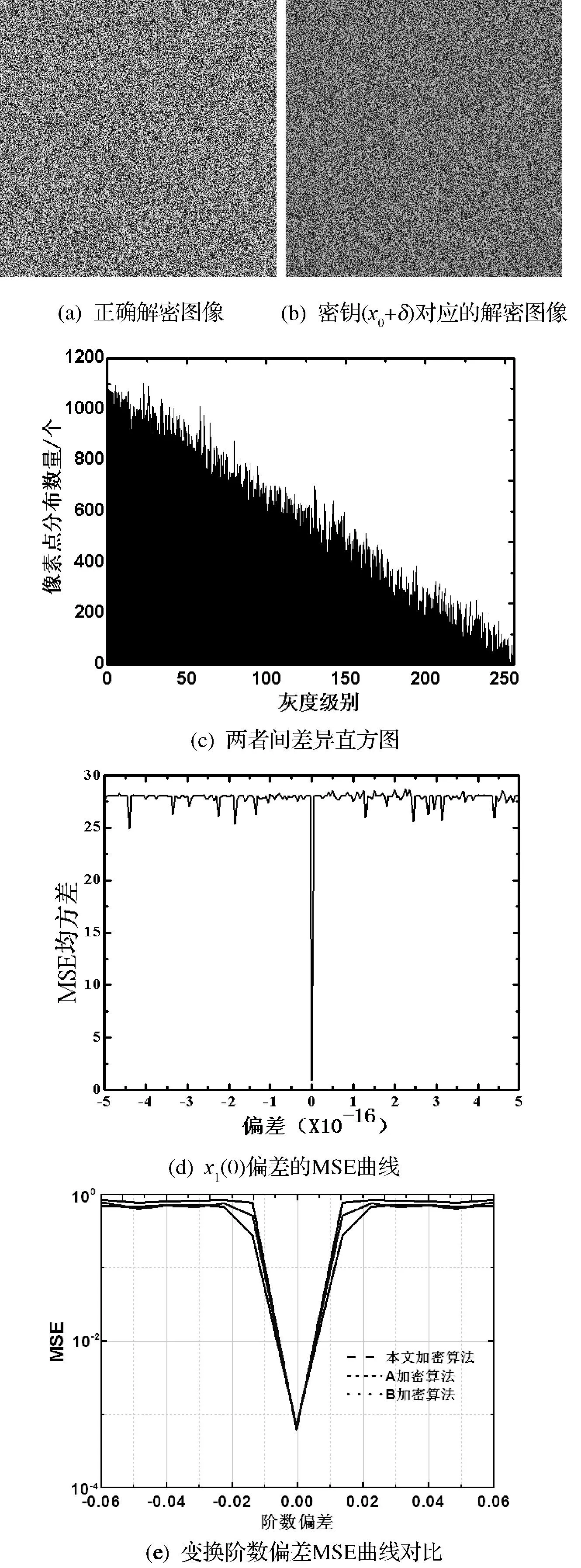
图5　密钥敏感性仿真实验测试结果

同时，本文引入像素改变率(NPCR)与归一化像素值平均改变强度(UACI)来对密钥敏感性进行测试评估。NPCR与NPCR的计算公式如下[14,15]：

(20)

(21)

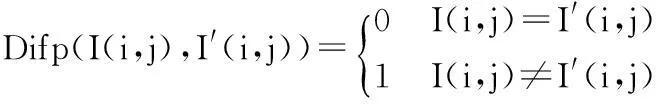
(22)

经计算获得NPCR= 99.89%，UACI=33.48%，均大于A、B算法的NPCR与UACI(见图6与表2所示)，可见本文算法具有更强的抗差分攻击能力、更高的加密效率。

图6　UACI以及NPCR的测试结果

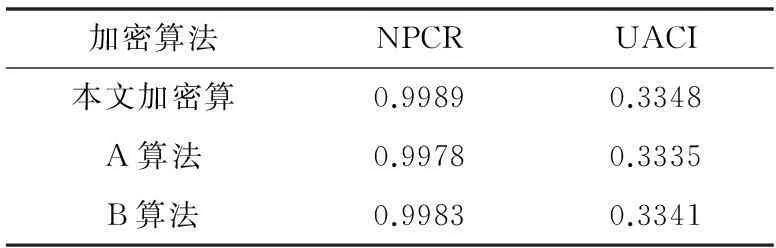
加密算法NPCRUACI本文加密算0.99890.3348A算法0.99780.3335B算法0.99830.3341

3.5相邻两像素点的相关性分析

大量研究表明，高度安全的加密系统可以有效消除相邻像素点间的相关性。在初始图像与密文图像中分别随意择取3000对相邻像素点计算其相关系数RXY，计算模型如下：

(23)

其中，X与Y表示为图像相邻像素点的灰度值；σX、σY分别表示为X、Y的标准偏差；μX、μY分别表示为X、Y平均值。

图像在对角线、水平、垂直这三个方向的相邻像素点间的相关性测试结果如表3所示，从表中可以看出，密文图像相邻像素点的相关性较低。图7是水平方向上的加密前后图像里任意两个相邻像素点的相关性测试结果。如图7(a)所示，明文图像的相邻像素值聚集为一条对角线(x=y)，这表明其相邻像素点间的相关性很高，得到的值达到0.9766；而经过本文算法加密后，其像素值呈现均匀分布，如图7(b)所示，说明本文算法能够以有效消除其相关性，得到的值为-0.0039，该值趋于0。

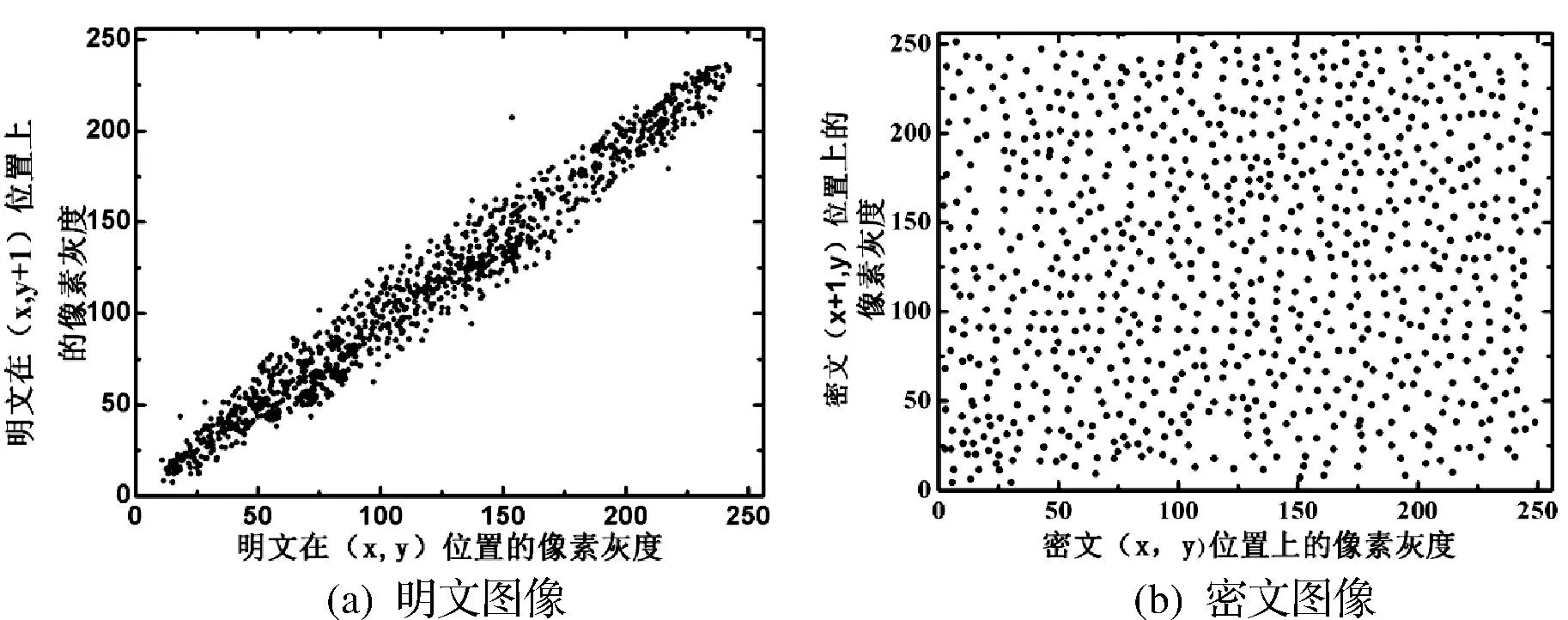
图7　相邻像素间相关性仿真结果

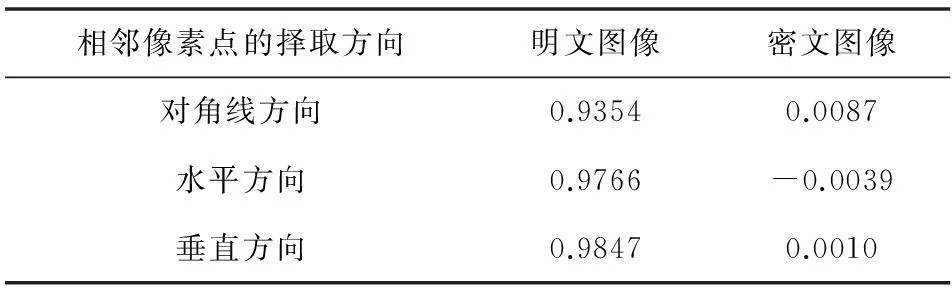
相邻像素点的择取方向明文图像密文图像对角线方向0.93540.0087水平方向0.9766-0.0039垂直方向0.98470.0010

4结语

针对目前的一些关于基于分数阶傅里叶变换的图像加密算法主要存在密钥敏感性及安全性较差的缺点，本文提出一种基于离散分数阶Fourier变换结合指数随机相位掩膜的加密算法。利用Logistic混沌映射进行置乱处理，加密过程采用了离散分数阶Fourier变换本征矢量分解的方法进行运算。最后给出了相关算法的安全性对比分析。仿真结果表明:与其他加密机制相比，本文加密系统兼顾了更强的密钥敏感性以及更高的安全性。

参考文献

[1] 任洪娥,戴琳琳,张健.基于混沌数列变换的图像加密算法[J].计算机工程与设计,2013,34(5):1615-1619.

[2] 郭雨,柏森,阳溢.基于复用技术和数论的图像加密压缩同步算法[J].电视技术,2013,37(5):33-37.

[3] 许爽,王伟,苏玉.基于双向扩散机制融合伪随机数同步生成器的快速图像加密算法研究[J].科学技术与工程,2014,14(3):45-50.

[4] 龚黎华,曾邵阳,周南润.基于2D Arnold变换与频谱切割的彩色图像加密算法[J].计算机应用,2012,32(9):2599-2602.

[5] Nshchal N K,Joseph J,Singh K.Securing information using fractional Fourier transform in digital holography[J].Optics Communications,2004,235(6):253-259.

[6] 李孟涛,孙刘杰,李晨璐.基于小波变换的傅里叶加密印刷水印算法研究[J].包装工程,2012,23(15):22-24.

[7] Zhou Y C,Bao L,Chen C L P.Image encryption using a new parametric switching chaotic system[J].Signal Processing,2013,93(11):3039-3052.

[8] Li L,Abd El-Latif A A,Niu X.Elliptic curve ElGamal based homomorphic image encryption scheme for sharing secret images[J].Signal Process,2012,38(92):1069-1078.

[9] 何俊发,李俊,王红霞.不对称离散分数阶傅里叶变换实现数字图像的加密变换[J].光学技术,2005,31(3):410-412.

[10] 崔得龙,肖明,左敬龙.一种基于分数阶傅里叶变换的改进图像加密算法[J].成都信息工程学院学报,2010,25(1):22-26.

[11] 王雅庆,周尚波.基于分数阶Fourier变换的数字图像加密算法研究[J].计算机应用研究,2011,28(7):2738-2741.

[12] Ahmed A,Abd El-Latif,Li Li,et al.A new approach to chaotic image encryption based on quantum chaotic system,exploiting color spaces[J].Signal Processing,2013,93(11):2986-3000.

[13] Zheng H,Yu S,Lü J.Design and ARM Platform-Based Realization of Digital Color Image Encryption and Decryption via Single State Variable Feedback Control[J].International Journal of Bifurcation and Chaos,2014,24(4):1013-1018.

[14] Wang Zhen,Huang Xia,Li Yuxia,et al.A new image encryption algorithm based on the fractional-order hyperchaotic Lorenz system[J].Chinese Physics B,2013,22(1):10504-10509.

[15] Joshi M,Shakher C,Singh K.Logarithms-based RGB image encryption in the fractional Fourier domain:a non-linear approach[J].Optics and Lasers in Engineering,2009,47(6):721-727.

中图分类号TP391

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.02.074

收稿日期：2014-07-02。黑龙江省新世纪高等教育教学改革工程项目(JG2013010437)；黑河学院高等教育教学改革项目(Xjg1303)。田玉萍，副教授，主研领域：图像处理，线性代数。