高速铁路加权复杂网络特性分析

张兰霞，秦勇，王莉

(1.北京交通大学 轨道控制与安全国家重点实验室，北京 100044；

2.北京交通大学 交通运输学院，北京 100044)



高速铁路加权复杂网络特性分析

张兰霞1，2，秦勇1，2，王莉1，2

(1.北京交通大学 轨道控制与安全国家重点实验室，北京 100044；

2.北京交通大学 交通运输学院，北京 100044)

摘要:根据2015年中国高速铁路列车运行时刻表，提取全路479个高速车站和2 487次列车作为研究对象，运用复杂网络理论构建高速铁路地理网、车流网以及服务网3个网络模型。对各网络的节点度、聚集系数和平均网络距离等静态指标以及本文提出的节点强度、平均时间网络距离等指标特性进行分析。研究结果表明：高速铁路地理网仍具有树状网络的特点；高速铁路车流网的度分布符合指数分布规律；高速铁路服务网节点强度与度之间存在显著的幂律关系，具有无标度和小世界网的网络特点。在此基础上，研究在不同攻击情况下的高速铁路地理网络的可靠性，为提高高速铁路网络稳定性提出建议。研究结果可为未来设计和优化高速铁路网络结构方面提供借鉴和参考。

关键词：高速铁路；加权复杂网络；车流；平均时间网络距离；网络可靠性

铁路运输是我国交通运输行业的重要组成部分，承担着我国的5%的客运量和11%的货运量，支撑着我国国民经济的可持续发展。现已初步形成“四纵四横”为主，区域交通为辅的高速铁路网络。截止2014年底，中国高速铁路运营里程达到1.6万 km，高铁成为铁路客运的主力军。高速铁路依托于网络型的固定设施来完成客货运输任务，从复杂网络的角度对高速铁路成网条件下的结构特性进行分析，有助于了解高速铁路旅客列车的运营状况，为旅客运输组织提供参考，同时为高速铁路运输组织的优化提供了一种新的思路。近年来，复杂网络的研究已经逐步深入到物理学、管理科学和系统科学、社会科学等多个领域，建立了越来越多的演化模型来描述真实世界中存在的网络[1-3]。大量学者同时将复杂网络的研究深入铁路运输领域，赵伟等[4]对2005年的中国铁路地理网和车流网的分析表明我国铁路地理网是树状网络，而车流网是具有无标度特性的小世界网络；Li等[5-7]用不同的方式对铁路网络建模，也得到了类似的结论。此外，印度铁路车流网[8]同样被证明为小世界网络。这些研究为探索全国铁路网的无权或加权网络的宏观特性提供了基础，但对基于复杂网络理论的高速铁路网络的拓扑特性与高速铁路运输组织之间的关系研究较少。

本文针对2015年的全国铁路时刻表及高速铁路建设相关数据，抽取高速铁路网络构建中的所需数据，构建了高速铁路地理网、车流网和服务网模型。选取表征网络静态统计特征的节点度、平均网络距离、聚集系数以及基于加权网络的最短时间网络距离等新建指标，从运输组织的角度探讨中国高速铁路地理网、车流网以及服务网的拓扑性质。并且重点分析高速铁路服务网的拓扑特性，研究在不同攻击情况下高速铁路网特征参数的变化，对高速铁路地理网络的可靠性进行详细的分析，为提高我国高速铁路运营网络稳定性提供了基础的指导建议。

1高速铁路复杂网络的构建

1.1高速铁路数据分析

欧洲铁路联盟对高速铁路的定义为[9]：在新建高速专用线上运行时速至少达到250 km的铁路，或在旧线改造时速达到200 km的铁路。根据我国铁路实际运行情况，我国高速铁路大致分为3类，即城际铁路、新建高速铁路以及既有线改造后的高速铁路。高速铁路地理网建设过程中，随着交通网络的日益完善，高速铁路运行线路逐渐成网。为方便计算同时不影响分析结果，本文对高速铁路网络做如下处理：1)由于高速铁路路网上下行开行对数大致相同，处理为无向网络；2)同一枢纽，根据各车站间是否存在联络线或者是否有经停列车，来确定两站之间的连接状态；3)为避免出现不连通图影响实验结果，本文删除了高速铁路网络中某些不连通的车站和线路。

对比分析2010年中国高速铁路网时刻表数据可知，“C”字头的列车开行70趟，“D”字头的列车438趟。而截止2015-06，我国高速铁路网包括479个车站，2 487个车次，其中动车组959趟，高速动车1 062趟，城际高速466趟。相较于2010年高速铁路网络规模明显增长。

1.2高速铁路网络构建模型

将车站看成是节点，把连接2个车站之间的轨道看成是连接2个站点的“边”，这样构成的网络称为高速铁路地理网[10]。高速铁路地理网是铁路旅客运输的基础，本文从高速铁路运行时刻表中提取高速铁路线路的车站及车站间的连接关系，构建的高速铁路地理网络中共有479个车站，570条边。将车站作为网络中的节点，如果存在同一列车经停某2个车站，则认为这2个车站之间存在一条边，这样构成的网络称为高速铁路车流网。同样从高速铁路运行时刻表中，分析车流网的车站及车站之间的连接关系，构建出包含68 198条边的高速铁路车流网络。同车流网的构建方式相同，但是为进一步表征高速铁路车流对路网的影响，将车站间经停的列车数目定义为边的权重，以此构建铁路服务网。

1.3高速铁路网基本指标

节点i的度定义为与节点i连接的其他节点的数目[11]。度越大，表示节点i与其他节点直接连通的路段数就越多，节点自身在路网中的影响就越重要，计算公式如下：

(1)

nij设计为0～1变量，表示节点i和j之间是否存在边相连。度分布p(k)表示在网络中任意选出一个点，其度值为k的概率。

聚集系数是一个点的邻接点之间相互连接的假设网络中的一个节点i有ki条边将它和其他节点相连，这ki个节点实际存在的边数Ei和总的边数ki(ki-1)/2之比就定义为节点i的聚类系数，即：

(2)

网络中2个节点i和j之间的距离dij定义为连接这2个节点的最短路径的边数。网络的平均路径长度定义为任意2个节点之间的距离的平均值，N表示网络中节点的个数，则：

(3)

以上这些指标都是无权网络中的静态统计量。加权网络对边或点赋予权重，为描述网络性质提供了新的维度。本文在充分利用这些静态指标的基础上，加入能表征高速铁路网络的运营特性，构建了新的指标体系。

2高速铁路加权网络特性分析

2.1高速铁路地理网的特性分析

2.1.1车站度分布

在高速铁路地理网中，车站节点度越高与该车站连接的相邻车站越多，表明该车站具有较好的交通优势。利用式(1)中节点度的定义设计java程序求解2015年与2010年车站的度分布曲线，如图1所示，其分布规律形态与2010年分布相似。2015年高速路网中节点度最高为6，均值为2.11，说明平均一个车站与其他2个车站直接相连。由图1可以看出，度为1车站减少，说明边缘车站的连通性有所提高，节点度为3，4和5的车站数相比之前有了一定增长，说明中国高速铁路经过5 a的建设，车站之间的地理连接较之前相对紧密。

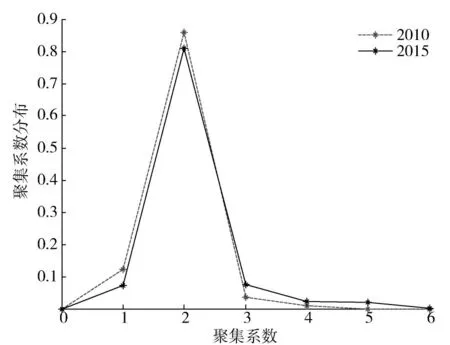
图1　高速铁路地理网度分布

Fig.1 Degree distribution for high-speed railway geographical network

2.1.2车站聚集系数分布

车站聚集系数研究的是车站间连接的紧密程度，网络聚集系数越大，说明节点与附近各个节点的连接紧密度越高，即实际高速车站间的线路连接越密集。利用式(2)中聚集系数的定义设计java程序求解2015年中国高速铁路地理网的聚集系数分布曲线，如图2所示，其中高速铁路地理网的平均聚集系数为0.01，绝大部分车站节点聚集系数为0，也即是很少有3个车站之间存在相互连接的关系，说明中国高速地理网络较为稀疏，一旦发生突发事件将导致列车绕行多个车站，对运输组织的影响较大，中国高速铁路还有很大的发展空间。

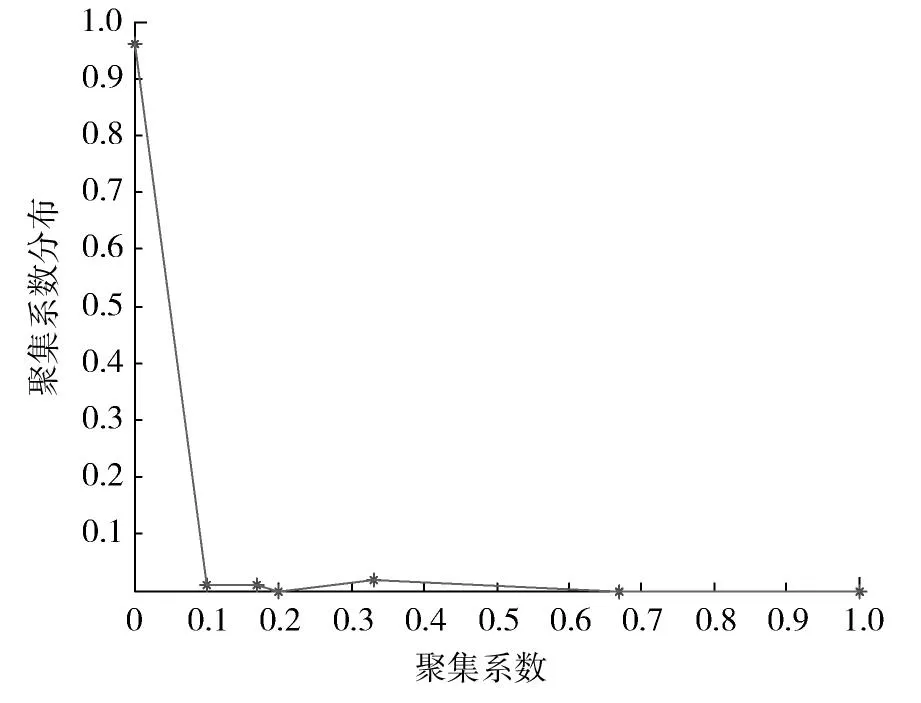
图2　高速铁路地理网集群系数分布Fig.2 Cumulative distribution of clustering coefficient for high-speed railway geographical network

2.1.3车站最短路径长度分布

本文构建的高速铁路地理网络中，在复杂网络的定义下网络距离反映了高速铁路网络中任意2个站点之间平均需迁移多少个节点，也即是旅客从出发地到目的地列车所经过的车站个数，是一个能间接表示高速铁路网络通达性的重要指标。根据式(3)中平均网络距离的定义，采用Dijkstra算法设计java程序计算得中国高速铁路地理网最短路径长度分布，如图3所示。2015年高速铁路平均网络距离为30.84，即从任意一个车站出发到达其他车站平均需经过31个车站，经过超过31个车站才能到达的线路主要是由于始终点车站均处于高速铁路路网的边缘。但是相较于高速路网中存在的479个车站的网络规模，仍然体现出小世界特性。高速铁路地理网最短路径长度分布近似于正态分布，但网络距离小于20的线路数量相对较少，其中30.7%的出行选择需经过的车站在20个车站之内，与我国高速铁路发展的现阶段状况相适应，但是相较于同年的航空网络地理网络的平均路径长度[12]，高速路网的便捷性还有待提高。

若考虑实际高速铁路距离，任意两车站之间的实际网络距离分布如图4所示。根据计算结果可得广州到大连最大网络距离达到4 740 km，而路网实际平均网络距离为519.90 km，这与我国国土面积跨度有关。从图4可以看出实际网络距离偏低的路径占有较大比重，相反实际网络距离较高的路径比例一般较小，随着高速路网的逐渐完善路网实际平均网络距离必然呈下降趋势，而实际网络距离的分布将趋于稳定。

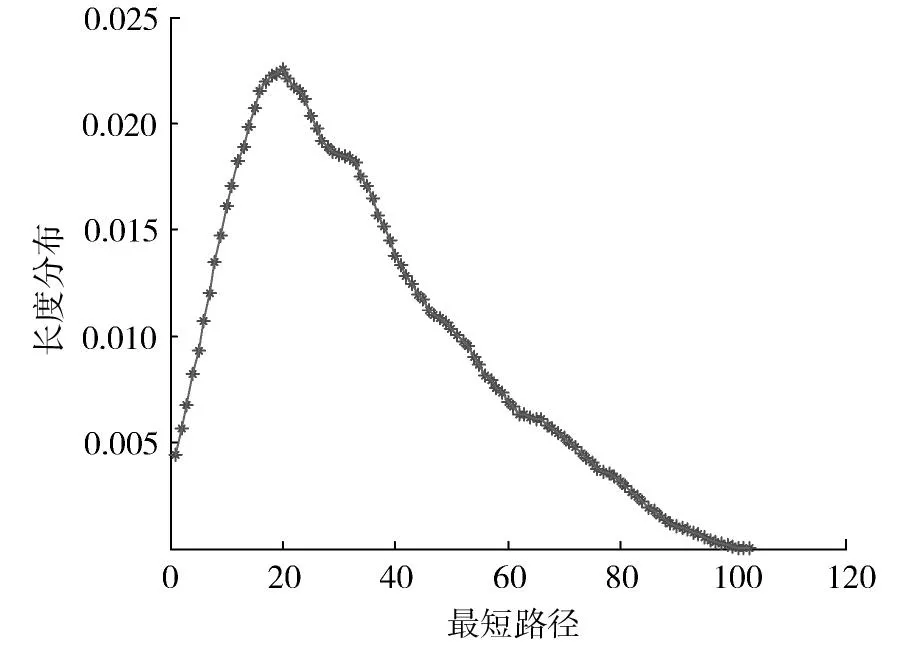
图3　高速铁路地理网最短路径长度分布Fig.3 Shorest distance distribution for high-speed railway geographical network

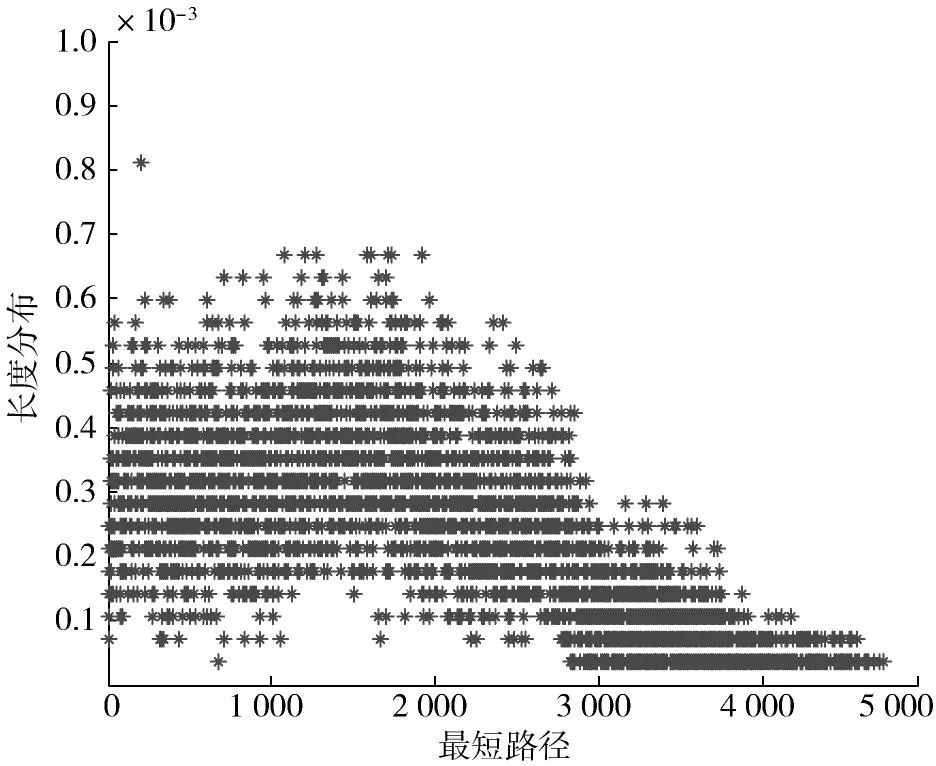
图4　高速铁路地理网实际最短路径长度分布Fig.4 Real shorest-distance distribution for high-speed railway geographical network

2.2高速铁路车流网的特性分析

2.2.1车站度分布

通过对高速铁路车流网模型的分析计算可知，高速铁路车流网中车站度值大于150的仅占2%，而且几乎都是多线交汇的枢纽车站如上海虹桥、南京南、武汉和杭州东等，但是仍有个别大型枢纽度值小于150，主要是为了体现这些枢纽内各车站的车流分布情况，各车站没有合并考虑。例如北京站，北京南站和北京西站的度值分别为29，121和94，三站构成的北京交通枢纽度值总计为234，大于车流网中上海虹桥车站的最大度值223；北京南站车流量大于北京站和北京西站的共同车流量，说明北京南站承担着北京枢纽内50%以上的高速客流运输任务，在枢纽中承担的高速客流较重，在运输组织中属于重点车站。根据图5可知相较于车流网中的较大度值，全国高速铁路网中大部分车站度值分布较低并且相对集中，94%的节点度值在120以内，50%的节点度值在44以内。从图6中的累积度分布可以得出，高速铁路车流网更加符合指数分布，这与2010年的中国铁路车流网的结果相似[13]，同样具有显著的小世界特性。说明现阶段中国高速铁路的发展状况与2010年中国铁路网的发展状况相似，但是高速铁路从2008年建立仅仅经历了7 a的建设时间，表明中国高速铁路的发展飞速。

图5　高速铁路车流网度分布Fig.5 Degree distribution for high-speed railway train flow network

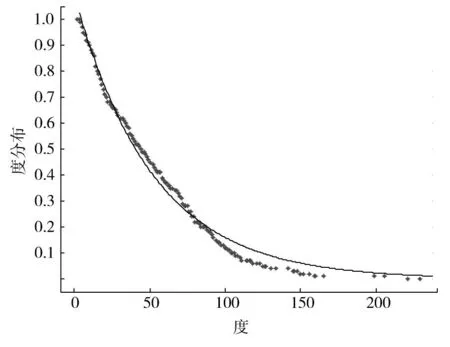
图6　高速铁路车流网累积度分布Fig.6 Cumulative degree distribution for high-speed railway train flow network

2.2.2车站聚集系数分布

通过计算得高速铁路车流网的平均聚集系数为0.697，表现出高聚集特性，图7表示为高速铁路车流网聚集系数分布。各节点聚集系数与度的关系如图8所示，数据反映各个车站相邻车站的连接程度相当高，而且整个网络中聚集系数为1的都是度值很低的车站，总体趋势表现为度值越低的车站其聚集系数越小，两者呈现出负相关的特性。

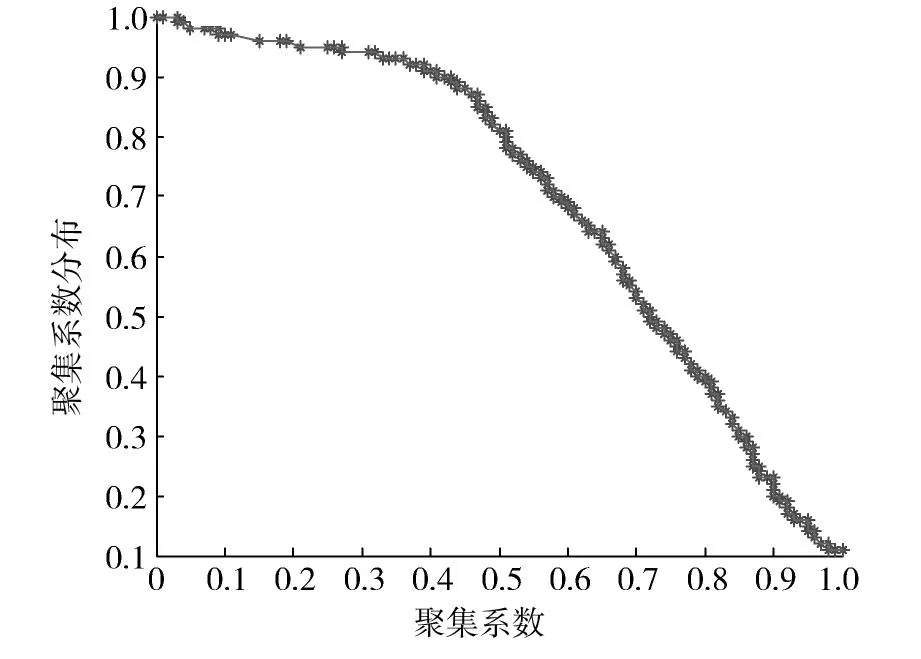
图7　高速铁路车流网聚集系数分布Fig.7 Cumulative distribution of clustering coefficient for high-speed railway train flow network

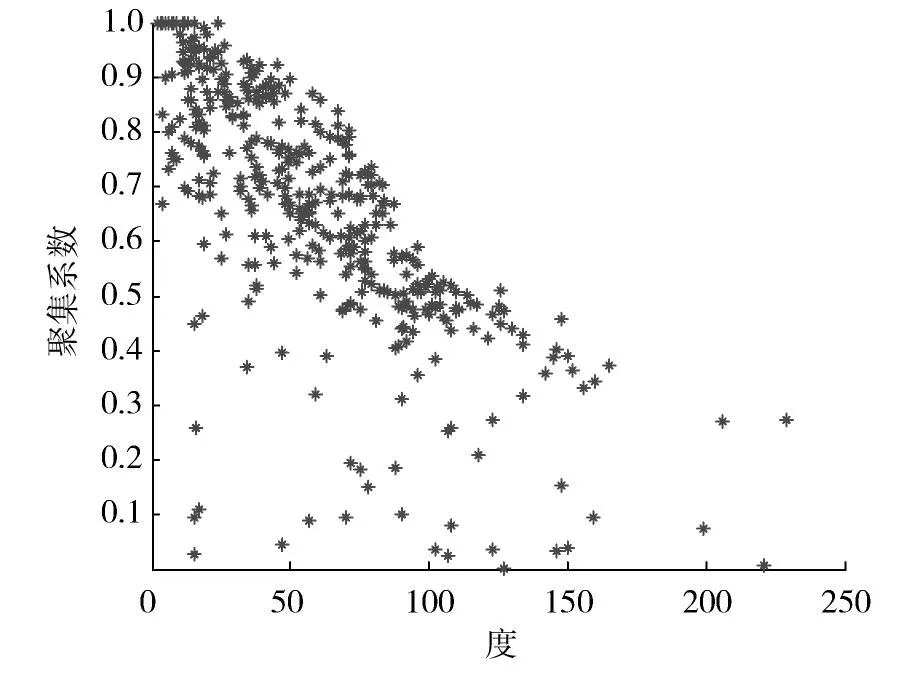
图8　高速铁路车流网聚集系数与度分布Fig.8 Cumulative distribution of clustering coefficient versus degree for high-speed railway train flow network

2.2.3车站最短路径长度分布

高速铁路车流网的平均网络距离间接反应了旅客一次出行的平均换乘次数，高速铁路车流网的平均最短路径长度为2.89，表明旅客从任意车站出发平均经1.89次换乘即可到达目的地。2015年中国高速铁路网车站间可直达的效率相较于2010年已经有大幅度的提升。但是从图9可以看出，换乘超过2次才能到达的出行路径也超过了71.2%，甚至有些站点之间最少换乘7次才能到达，表明中国高速铁路网的边远地区的建设远远不能满足乘客需求，针对换乘次数较大的节点之间应考虑增加高速铁路建设力度，充分发挥中国高速铁路的整体优势，最大限度满足乘客出行需求。

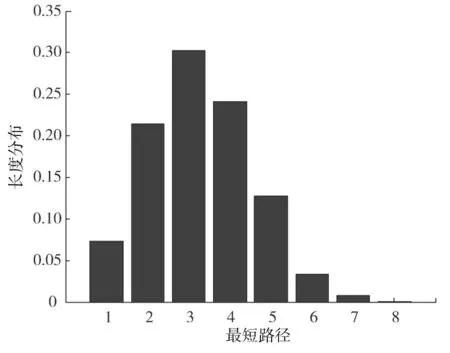
图9　高速铁路车流网最短路径长度分布Fig.9 Shortest distance distribution for high-speed railway train flow network

2.3高速铁路服务网的特性分析

2.3.1车站强度分布

车站强度间接反应了车站的服务能力，表明旅客从该车站出发不需要转车即可到达的其他车站的方便程度。车站强度与列车的开行频率密切相关，车站强度越大表示在实际高速铁路网络中该车站通行车流量越高，对应于高速铁路中车流量较大的换乘车站。图10显示了高速铁路服务网强度分布曲线，经统计，4.59%的车站强度大于1 000，60.04%的车站强度小于200，表明车站节点强度分布极为不均，换乘方便程度较高的车站数量相对较少，但是这些数量极少的高强度车站加强了网络的通达性，为满足高速铁路客运能力发挥着较大作用。如何综合考虑车站之间的连接以及车站之间通过的车流量，即如何协调车站强度以提升旅客出行服务是未来高速铁路路网运输组织工作的重点。

2.3.2车站强度-度分布

整体来看，在双对数坐标下的度为k的节点对应的平均节点强度s分布如图11所示，得到方程为：s∝k1.242，回归系数R2=0.9，表明二者具有幂律分布，并且指数1.242大于1表明强度的增长速度远快于度的增长速度，并且2者均为无标度网络。根据表1可知，南京南强度达到最大为3 088，远远大于上海虹桥的最大度229，而且节点强度和度排序并不完全相同，这主要是由于车站强度是由经停车站的列车数量以及车站节点度共同决定的，尽管南京南、杭州东、汉口和合肥南等车站节点度分布低于上海虹桥和杭州东等车站，但是这些车站的经停列车数量较高，所以车站强度增长快于车站度的增长。对于高速铁路服务网中济南西和合肥南等站点每日经停的车流量较大，也即是在服务网中承担较大的运输荷载。而这些车站度值并不高，故其相邻节点所承担的运输荷载必然较大，一旦有突发事件影响这些车站的正常运营，将会导致相邻车站运输载荷的重新分配，进而产生级联失效，因此在铁路日常运营生产中这些车站的维护保养也应加强。

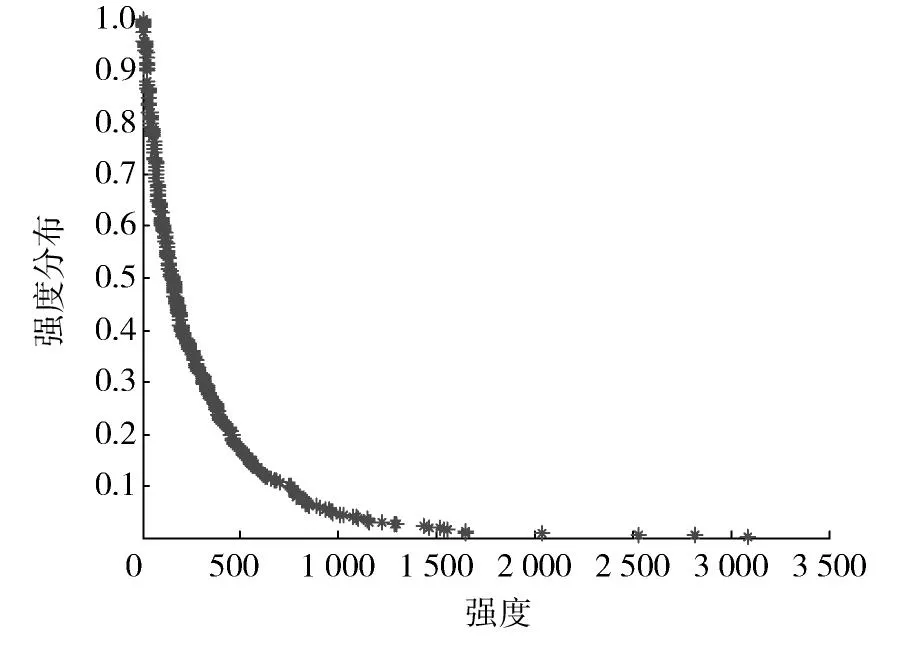
图10　高速铁路服务网强度分布Fig.10 Cumulative distribution of strength for high-speed railway service network

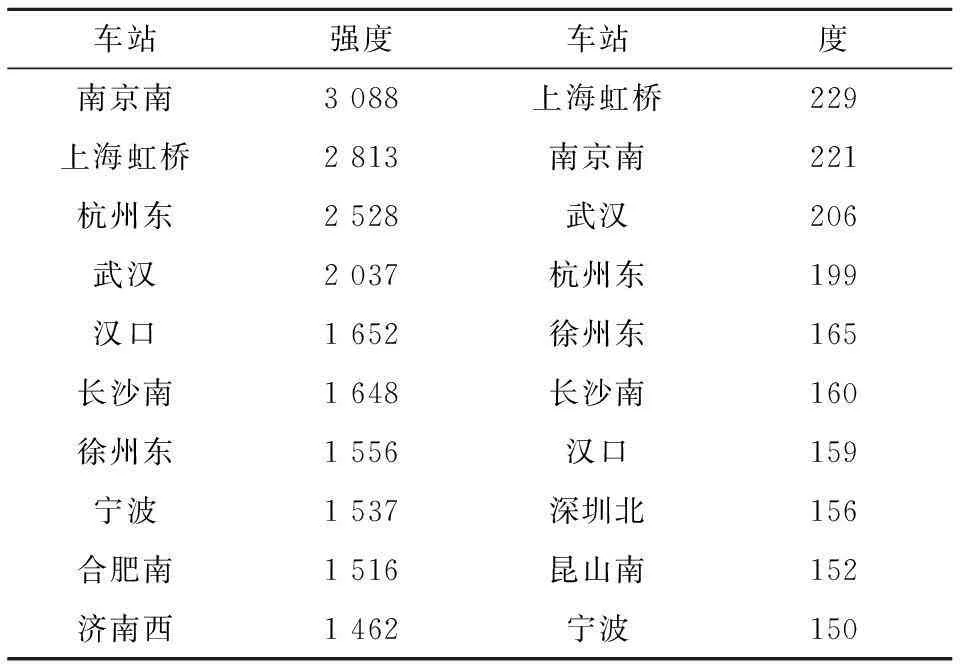
车站强度车站度南京南3088上海虹桥229上海虹桥2813南京南221杭州东2528武汉206武汉2037杭州东199汉口1652徐州东165长沙南1648长沙南160徐州东1556汉口159宁波1537深圳北156合肥南1516昆山南152济南西1462宁波150

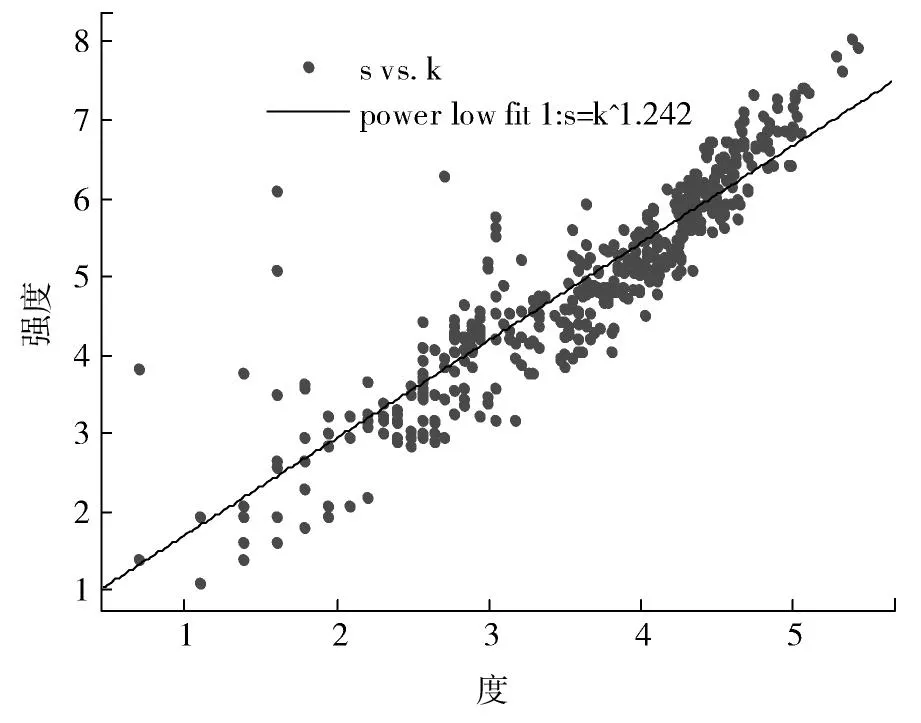
图11　高速铁路服务网双对数坐标下的强度及度分布Fig.11 Strength versus degree distribution for high-speed railway service network in log-log scale plot

2.3.3车站最短时间网络距离分布

在高铁铁路服务网中，不考虑边权的最短路径是指旅客换乘次数最少的路径，该种情况下的最短路径长度仅仅考虑旅客出行所需经停的车站以及旅客换乘的便利程度。车站i到j之间的路径并不一定是旅客的最佳出行路径；车站之间拥有的边权为经停车站而通过的车流量，相应带权的高速铁路服务网的平均网络距离是指边权之和最短的路径，也即是旅客出行路径上所经过的最少车流量，该种情况下的最短路径忽略了经停车站之间的实际距离以及旅客出行所关注的时间问题。为了同时反映铁路运行部门的运输组织优劣及旅客出行的时间效应，本文基于上述2种最短路径的理念提出路网平均时间网络距离的概念，定义考虑路径阻抗系数的线路最短时间网络距离，进而得出旅客出行所需的平均时间网络距离如下：

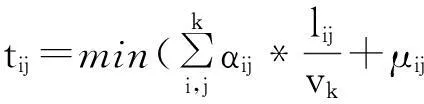
(4)

μij=lij-1

(5)

(6)

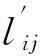
本文中旅行速度vk对应高速动车，城际高速和动车组分别取值为280，200和130 km/h；根据历史经验，同车站一次换乘时间t取值为70 min；αij根据区间通过的车流量确定，本文将区间通过的车流量采用归一化的处理方式转化为无量纲数据，令αij=βij+1表示区间车流量的大小对旅客出行时间的影响，βij区间i和j之间的车流量归一化之后的值。根据式(4)～(6)对旅客出行所需的平均时间网络距离的定义，设计java程序得如图12所示的高速铁路服务网最短时间网络距离分布曲线。

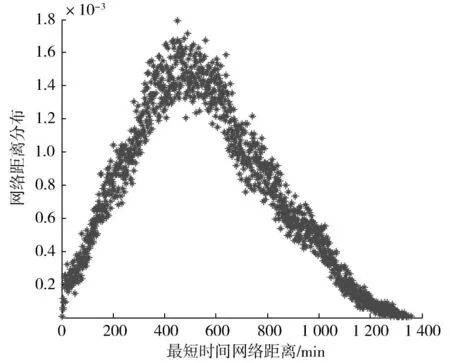
图12　高速铁路服务网最短时间网络距离分布Fig.12 Shortest time distance distribution for high-speed railway service network

通过计算可得不考虑出行换乘时间情况下，全国高速铁路网的平均时间网络距离为534.9 min，合计8.9 h。考虑换乘时间情况下，高速铁路网的平均时间网络距离为637.5 min，合计小时10.6 h。而且根据图12可知，高速铁路服务网时间网络距离的分布表现为近似高斯分布。

3高速铁路地理网的可靠性研究

3.1高速铁路地理网可靠性分析

网络可靠性是分析在随机和选择性攻击下网络的特性变化情况[14-16]。一般地，网络可靠性可以利用平均距离长度以及网络规模等指标进行研究，但是对于中国高速铁路网来说，旅客更在意突发事件下是否影响其正常出行，例如路网是否仍然连通、换乘次数是否增加等信息。因此，本文采用平均网络距离以及相对网络效率2个指标进行可靠性的分析。式(7)和(8)是相对网络效率的计算公式：

(7)

(8)

式中：N为遭受攻击后的网络中节点个数；dij表示i和j之间的网络距离；E表示遭受攻击状态下的网络连通效率；当i和j之间不连通，则dij=+∞，而eij=0；E0表示初始状态下网络的连通效率。

为研究高速地理网的可靠性，根据式(3)，(7)和(8)对平均网络距离以及相对网络效率的描述，本文利用java程序分别在随机攻击和选择性攻击下对高速铁路地理网可靠性进行分析。图13和14分别是2种攻击模型下高速铁路地理网平均网络距离和相对网络效率的对比曲线。

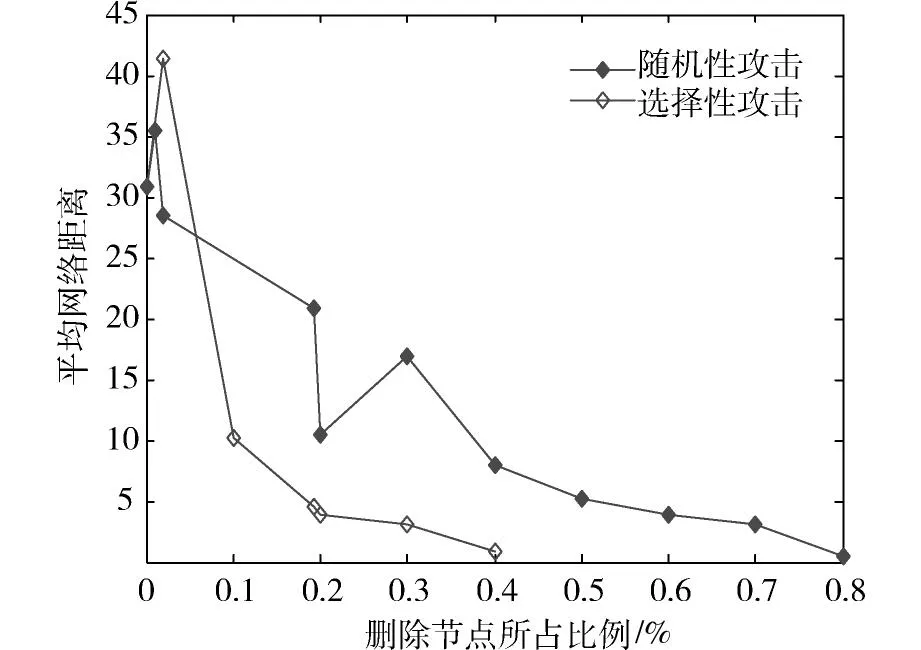
图13　2种攻击模式下高速铁路地理网的平均网络距离变化曲线Fig.13 Average network distance under the random and deliberate attacks for high-speed railway geographical network

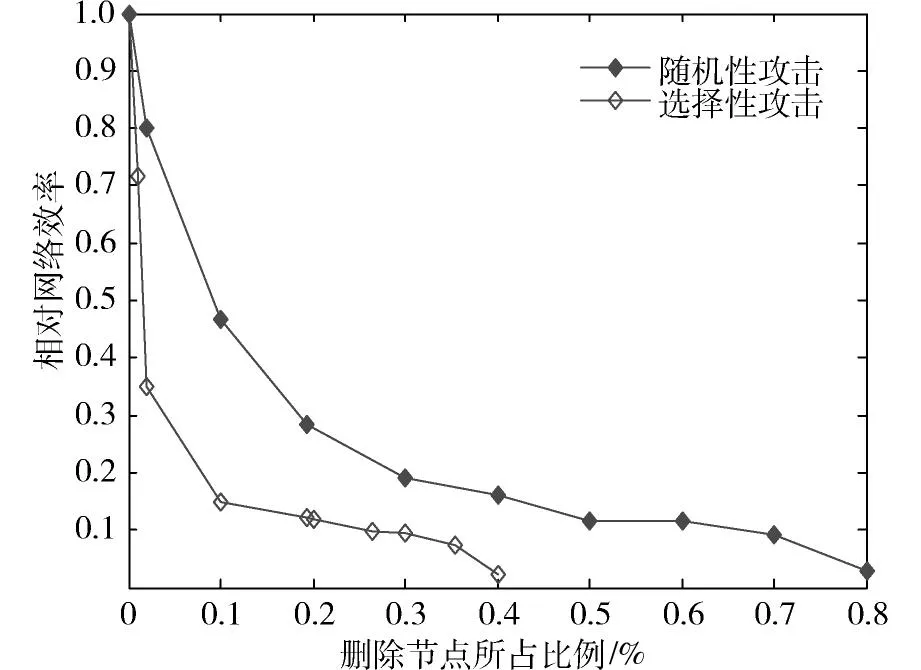
图14　2种攻击模式下高速铁路地理网的相对网络效率变化曲线Fig.14 Relative network efficiency under the random and deliberate attacks for high-speed railway geographical network

前文已经计算得出高速铁路地理网在原始状态下，平均网络距离为30.84，此时网络效率为0.06，说明现阶段高速铁路地理网整体连通性及可靠性并不高，在高峰客流时段仍然会存在局部客流聚集等问题，网络结构还需要进一步的完善。从图14中可以看出高速铁路地理网在随机性攻击模式下相对网络效率与删除节点数目的关系变化曲线较为平缓，而在选择性攻击模式下反应较为剧烈。随着路网规模的不断下降，在选择性攻击模式下，删除路网中40%度值最大的节点时，网络的相对效率已经变为0，说明此时高速铁路网络已经完全瘫痪；而在随机性攻击时要破坏点80%的节点才会导致高速铁路网的完全失效。因此，高速铁路网在受到攻击时，选择性攻击比随机性攻击的对路网的连通性和可靠性打击更大，攻击的传播速度更快。

通过比较我国高速铁路地理网在不同攻击模式下的可靠性，可知这与目前我国高速铁路地理网仍具有树状网络的特点有关。由于树状网络对各个节点对根节点的依赖性太大，在我国高速铁路地理网中，如果受到攻击的车站是少数树枝顶部的重要换乘车站，其下层车站将会处于局部连通状态，对我国高速铁路地理网的整体可靠性造成较大威胁。假设路网中树枝顶部的换乘车站均受到不同程度的攻击，将会产生大量的孤立站点，从而造成高速铁路地理网的瘫痪。当然，也正是由于目前我国高速铁路地理网仍具有树状网络的特点，可以充分利用树状网络的故障较易隔离的优点，可以在局部站点受到攻击的状态下，采用合理的运输调整策略，例如选择具有高速列车作业条件的既有线车站作为受到攻击的高速客运站的替代车站，从而使网络的整体可靠性得以保证。

3.2提高高速铁路网络稳定性的建议

根据高速铁路地理网可靠性分析结果，从2个角度出发为高速铁路网络运行稳定性提出优化建议。

3.2.1从高速铁路网络规划角度考虑

根据可靠性分析结果可知，随着高速铁路网的逐渐完善，网络的连通性逐渐增强，网络的抗毁能力也随之增加。为了防止关键车站遭到暴雨、泥石流等自然灾害的随机性影响，路网规划设计阶段，在结合路网高速铁路选址规划的同时也要提升非关键车站的重要程度，这样既均衡了路网重点车站的分布又缓解了关键车站的通过能力。结合高速铁路网的拓扑特性可知，尽管北京枢纽对路网连通可靠性影响很大，但是北京西站与北京南站之间并没有联络线，两任意车站受到攻击只能选择其他较远车站绕行，因此设计枢纽间联络线可以加强关键车站间的连通性，提高选择性攻击条件下既有线与高速铁路的跨线能力。结合路网可靠性分析，从上述两个方面出发优化路网结构，可以为高速铁路在突发事件运行稳定性提供保障。

3.2.2从高速铁路运输组织角度考虑

通过对高速铁路地理网的连通可靠性分析可知，关键车站一旦受到攻击，高速铁路网的整体连通性会迅速受到较大影响，为保证高速铁路的正常运行，需要对关键车站加强防护。如预见性地做好重点车站的雪灾防护工作、加开临客提升重点车站的大客流应对能力、保证重点车站的天窗时间等措施，均能维护高速铁路网络的稳定性。分析2种攻击模式下高速铁路地理网的相对网络效率指标可知，在两种攻击模式的初始阶段，网络的整体连通性较后期阶段下降迅速。因此在车站刚开始受到攻击时，各级部门应迅速采取积极的运输组织应对措施，如地震灾害一旦发生，立即对经过该区域的所有列车采取迂回、重联和停运等优化组合调整方案，避免大面积晚点传播，能有效地减少和遏制高速铁路网络连通可靠性的损失。

针对我国高速铁路车流网及服务网的稳定性，从上述2个方面出发进行路网车站等设备设施以及铁路现场组织人员的合理优化配置，也将会对我国高速铁路车流网、服务网的稳定性具有重要的保障作用。

4结论

1)利用2015年中国高速铁路时刻表，基于复杂网络理论分析了中国高速铁路网的拓扑特性，在对地理网、车流网和服务网等网络的统一研究下，得出了中国高速铁路服务网具有“小世界”和“无标度”等一般特性。

2)为分析中国高速铁路网的网络特性提供了一种定量的方法，便于铁路运营部门更好地掌控高速铁路整体网络的结构特性，为进一步扩展和完善高速铁路网提供理论依据。

3)根据平均网络距离以及相对网络效率两个指标对高速铁路地理网的可靠性进行了评价，为今后保证高速铁路网络稳定性提出了建设性的意见。

参考文献：

[1] Jeong H, Tombor B, Albert R, et al. The large-scale organization of metabolic networks[J].Nature, 2000(407):651-654.

[2] Andrade J S, Herrmann H J, Andrade R F S, et al.Apollonian networks:simultaneously scale-free,small world, euclidean,space filling,and with matching graphs[J].Physical Review Letters,2005,94(1):018702.

[3] Albert R, Barabási A L, Statistical mechanics of complex networks[J]. Reviews of Modern Physics, 2002, 74(1):47-97.

[4] 赵伟,何红生,林中材,等.中国铁路客运网网络性质的研究[J].物理学报,2006,55(8):3906-3911.

ZHAO Wei, HE Hongsheng, LIN Zhongcai, et al. The study of properties of Chinese railway passenger transport network[J].ACTA Physica Sinica,2006,55(8):3906-3911.

[5] Li W, Cai X. Empirical analysis of a scale-free railway network in China[J].Physica A,2007,382(2):693-703.

[6] 包云,刘军,李婷.中国铁路旅客列车服务网络性质研究[J].铁道学报,2012,34(12):8-15.

BAO Yun, LIU Jun, LI Ting. Properties of Chinese railway passenger train service network[J].Journal of the China Railway Society, 2012,34(12):8-15.

[7] 王伟,刘军,蒋熙,等.中国铁路网的拓扑特性[J].北京交通大学学报,2010,34(3):148-152.

WANG Wei, LIU Jun, JIANG Xi, et al. Topology properties on Chinese railway network[J].Journal of Bejing Jiaotong University,2010,34(3):148-152.

[8] Sen P, Dasgupta S, Chatterjec A, et al. Small-world properties of the Indiar railway network[J].Physical Review E,2003,67(3):1-5.

[9] EU. High-speed railway [EB/OL].[2010-06-30].http://finance.eastday.com/m /u1a5300869.html.

[10] MENG Xuelei, QIN Yong, JIA Limin. Comprehensive evaluation of passenger train service plan based on complex network theory[J].Measurement, 2014(58):221-229.

[11] 何大韧,刘宗华,汪秉宏.复杂系统与复杂网络[M].北京:高等教育出版社,2009:127-139.

HE Daren, LIU Zhonghua, WANG Binghong. Complex systems and complex networks[M].Beijing: Higher Education Press, 2009:127-139.

[12] WANG J, MO H, WANG F, et al. Exploring the network structure and nodal centrality of China’s air transport network: A complex network approach [J]. Journal of Transport Geography, 2011, 4(19): 712-721.

[13] 王莉,秦勇,徐杰,等.中国铁路车流网的拓扑性质[J].北京理工大学学报,2012(32)：84-88.

WANG Li, QIN Yong, XU Jie, et al. Topological property of china railway traffic network[J]. Journal of Beijing Institute of Technology, 2012(32):84-88.

[14] Holme P, Kim B. Attack vulnerability of complex networks[J]. Phys Rev E, 2002(65):56-109.

[15] Boccaletti S, Latora V, Moreno Y. Complex network: structure and dynamic[J]. Physica Reports, 2006(424):175-308.

[16] 蔡鉴明,李夏苗,杨光华.基于时变性和可靠性的地震灾害应急物流运输路径选择[J].铁道科学与工程学报,2011,8(5):101-106.

CAI Jianming, LI Xiamiao, YANG Guanghua. The routing problem for emergency logistics considering the reliability and time-varying in the earthquake disasters[J].Journal of Railway Science and Engineering, 2011,8(5):101-106.

(编辑蒋学东)

Statistical analysis of weighted complex network in Chinese high-speed railway

ZHANG Lanxia1,2, QIN Yong1，2, WANG Li1，2

(1. State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China;2. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China)

Abstract:According to the 2015 China's high-speed railway timetable, this paper extracted 479 high speed stations and 2 487 high speed trains as the research object. Based on complex network theory, three high-speed railway geographical network, train flow network and service network models were built. Through the analysis of the each network's node degree, aggregation coefficient, average network distance, and an node strength, average time-network distance etc, it is found that high speed railway geographic network still has the characteristics of tree network. The distribution degree of high speed railway wagon flow network is conform to the exponential distribution law. The relationship between the node strength and node degree of high-speed rail service network is a remarkable power-law, and it has the network characteristics of scale-free and small-world network. Then, this paper also analyzed the network reliability under the different attacks on high-speed railway network, and recommendations were put forward in order to improve the network stability of high-speed railway. The results provide a reference for the future design and optimization of high speed railway network structure.

Key words:high-speed railway; weighted complex network; train flow; average time-network distance; network reliability

中图分类号：U293.1

文献标志码：A

文章编号：1672-7029(2016)02-0201-09

通讯作者：秦勇(1971-)，男，江苏徐州人，教授，博士，从事智能交通系统，交通安全工程等研究；E-mail: qinyong2146@126.com

基金项目：国家科技支撑计划资助项目(2009BAG12A10)；铁道部科技研究开发计划课题资助项目(2013F022)；北京交通大学基本科研业务资助项目(2014RC031)

*收稿日期：2015-08-22