基于系统动力学的车辆器材库存需求量预测

何 健， 张大鹏， 文正中

(1. 军事交通学院研究生管理大队， 天津 300161； 2. 军事交通学院军用车辆系， 天津 300161)

基于系统动力学的车辆器材库存需求量预测

何 健1， 张大鹏2， 文正中1

(1. 军事交通学院研究生管理大队， 天津 300161； 2. 军事交通学院军用车辆系， 天津 300161)

针对车辆器材库存需求量预测存在的影响因素考虑不全和预测精度不高的问题，分析了影响库存需求量的主要因素及各变量之间的因果关系，建立了车辆器材库存需求量预测系统动力学模型，并进行了实例验证。结果表明：该模型考虑因素齐全，预测结果更接近实际，具有一定的参考和应用价值，为科学预测车辆器材库存需求量提供了新方法。

车辆器材；系统动力学模型；库存需求量预测

车辆器材是车辆装备维修保障的物质基础，准确预测车辆器材的库存需求量对提高车辆装备完好率具有重要意义[1]。然而，目前对车辆器材库存需求量的研究主要停留在理论计算方法上，对装备维修保障中库存需求规律和发展趋势研究相对较少。徐飞等[2]在分析装备使用情况和需求数据波动的基础上，运用粗糙集理论和层次分析法修正了灰色预测模型，该模型所需样本少，易挖掘出数据中隐藏的规律，但对需求波动性大、离散性强的器材库存需求量难以进行有效预测；罗晓萌等[3]基于时间序列法对历史数据进行了分析，同时考虑价格对需求的影响，预测了在一定服务水平下的库存需求量，该方法虽然得出了动态库存采购策略，但考虑的库存需求影响因素较少，预测偏差较大；楼增龙等[4]以实际统计数据为样本，建立了多元线性回归预测模型，该模型对于间断性需求或当需求数据量较小时，预测偏差较大。

系统动力学预测方法能够综合考虑各种影响因素，对于历史数据不足、复杂非线性问题均具有良好的预测效果，且可预测系统的发展趋势和波动周期。因此，笔者在系统全面分析库存需求影响因素的基础上，建立了车辆器材库存需求量预测的系统动力学模型，并通过实例验证模型的有效性，为科学筹措器材、管理库存提供支持。

1 车辆器材库存需求量影响因素分析

我军器材仓库正常周转的关键在于器材入库——保管——出库过程能够维持一定程度的动态平衡，为维持该动态平衡，必须准确预测库存需求量。库存需求量影响因素较多，主要有器材可靠性、器材运行环境、器材使用强度和维修保障水平等。笔者通过部队实地调研和专家评定，选取车辆装备规模、器材新增量和器材报废量3个参数来衡量上述因素对库存需求量的影响程度[5]。

1.1 车辆装备规模

车辆装备规模是指为完成某次任务所投入使用的车辆装备数，是影响库存需求量的基本因素。车辆装备规模越大，器材需求量会越大，相应的库存需求量也越大。此外，车辆装备规模还影响故障器材数量和器材新需求量，进而影响器材报废量；尤其是当受到战争爆发和上级授予紧急任务等其他无法预料的随机性因素影响时，车辆装备规模会突然增大，库存需求量会随之迅速上升。

1.2 器材新增量

器材新增量是指随着军事训练任务或车辆装备数量增多而需要增加的车辆器材数量，与车辆装备规模增加量和库存调整量有关，是影响库存需求量的重要因素。随着车辆装备规模的增加，所需储备的车辆器材就会增多，库存需求量也随之增大。近年来，我军担负的军事训练、演习任务越来越频繁，器材新增量不断提升，但整体增幅逐渐减小并趋于稳定。

1.3 器材报废量

器材报废量是指由于质量不符合技术标准而发生故障且失去修复意义或价值较低直接进行更换的车辆器材数量，其与故障器材数量和报废速率有关，是影响库存需求量的关键因素。随着车辆装备服役年限的增加，器材使用寿命将逐渐下降，器材报废速率逐渐加快，同时器材报废量会随之增大，库存需求量也随之增大。

2 车辆器材库存需求量预测系统动力学模型构建

2.1 预测流程

运用系统动力学解决实际问题的流程为：分析系统信息——理清系统变量间的关系——解决系统问题。这是一个由浅入深、波浪前进的过程，它从多个角度剖析问题，综合考虑各种影响因素，进而使预测结果更加科学、可靠。图1为车辆器材库存需求量系统动力学模型预测流程。

图1 车辆器材库存需求量系统动力学模型预测流程

2.2 变量之间因果关系分析

根据车辆装备实际运行状况和库存需求量影响因素分析结果，建立车辆器材库存需求量预测变量之间的因果关系，如图2所示。图中：“+”、“-”分别表示两变量间的关系为正相关、负相关。

图2 车辆器材库存需求量预测变量之间的因果关系

1) 器材报废速率是指单位时间内器材报废的数量，其与维修水平和使用年限有关。随着维修技术水平的不断提高，可维修翻新的器材数量随之增大，报废速率随之减小。

2) 器材新需求量是指在一定保障度的要求下，当车辆装备规模增大后所需增加的器材数量。新需求量主要受车辆装备规模影响，其随车辆装备规模的增大而增大。

3) 故障器材数量与车辆装备规模和器材故障率有关。车辆装备规模越大，需要维修或淘汰报废的器材基数就越大，故障器材数量也随之增大。

4) 器材库存需求量主要受新增量和器材报废量的影响。随着器材新增量和报废量的增大，器材库存需求量也随之增大。

主要反馈回路为：新增量→(+器材报废量→)+库存需求量→-库存调整→+新增量，即当器材新增量增大时，器材报废量增大，库存需求量就增大，为了使器材库存需求量达到理想状态但又避免积压浪费，需要调整库存，减少器材采购数量，抑制新增量增大[6]。

2.3 系统流程图

系统流程图可全面地反映系统的物质流、信息流和反馈作用。根据车辆器材库存需求量预测变量之间的因果关系，运用Vensim软件绘制车辆器材库存需求量预测系统流程图，如图3所示。

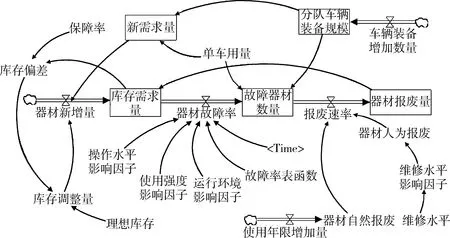
图3 车辆器材库存需求量预测的系统流程图

系统动力学模型中各符号及其含义如表1所示。

表1 模型中各符号及其含义

系统动力学模型中的主要方程如下：

N车辆装备规模=INTEG(车辆装备增加数量，X)。

T 车辆装备增加数量=WITH LOOKUP(time,数组)。

T 维修水平影响因子=WITH LOOKUP(维修水平，数组)。

L 器材新增量=新需求量+器材调整量。

L 新需求量=车辆装备增加数量×单车用量。

L 理想库存=SMOOTH(需求量，移动平滑时间)。

L 器材报废量=故障器材数量×报废速率。

L 报废速率t=自然报废速率t+人为报废速率t。

其中：报废速率包括自然报废速率和人为报废速率。报废速率t为器材使用t年后的报废速率。由于器材发生报废后要求立即进行更换和补充，则在第t年，整个车辆装备系统中将包含使用1～t年的器材。一般运用排队论来求解第t年的报废速率。

L 库存需求量=器材新增量+器材报废量。

A 库存偏差=(理想库存-器材需求量)×(1-保障率)。

A 库存调整量=库存偏差。

R 自然报废速率t=β(t-1)-β(t)。

自然报废指随着使用年限的增加，器材寿命达到极限而产生的报废，主要与使用时间有关。β(t)为器材使用t年后的自然完好率，一般用双参数Weibull分布函数来计算[7]，即β(t)=exp((-t/T)k)。其中：T为某种器材的平均使用寿命；k为特征参数。

R 人为报废速率t=σ×器材故障率。

人为报废是指故障器材中因无法进行人为修复而导致的报废，主要受维修水平和器材故障率影响。当某种器材的关键性、价值较低，对故障件直接进行更换时，则σ=1,人为报废速率=器材故障率；当某种器材有修复价值时，则σ=1-维修水平影响因子，此时，人为报废率与维修水平有关。

T器材故障率=故障率表(time)×使用强度影响因子×运行环境影响因子×操作水平影响因子。

3 实例分析

3.1 参数及变量确定

以2005年列装部队的运输车解放CA1121的XX器材为研究对象，其单车用量为2件，且具有修复价值。以其10年的需求及故障数据为预测样本，保障率为0.99。由于部队保障任务的不间断性，当器材消耗后必须立即进行补充，因此，不考虑时间延迟。部队进行器材采购的周期通常为1年，在采购周期内，XX器材的理想库存量即为年期望需求量。通过移动平滑法，应用前5年的库存需求量来预测该器材下一年的理想库存量[8]。解放CA1121的装备规模及相关数据如表2所示，其中车辆装备工作时间用来度量其使用强度影响因子的大小。车辆装备数量增长率的表函数如图4所示，其中：横坐标为年份；纵坐标为车辆装备增加数量。

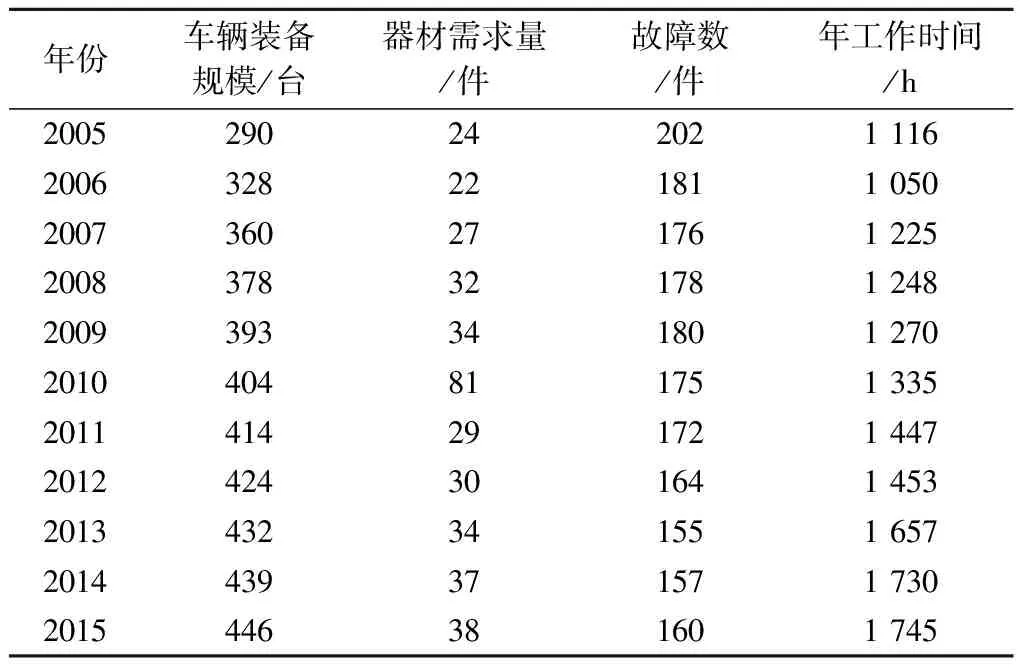
表2 2005-2015年某器材仓库解放CA1121的装备规模及相关数据

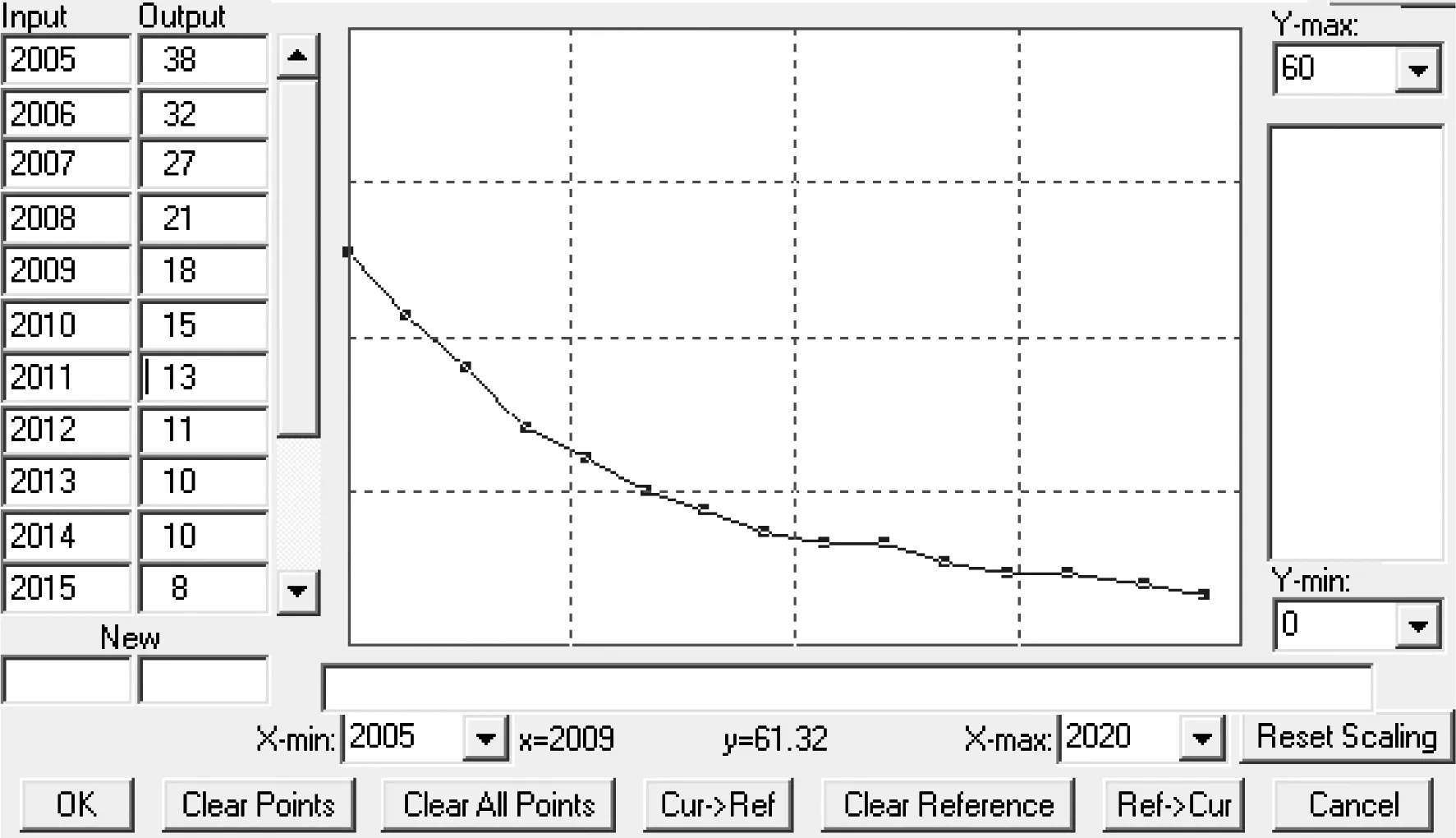
图4 车辆装备数量增长率表函数

器材的报废速率不仅受车辆使用年限的影响，而且受维修水平和器材故障率的制约。根据张鹏等[9]的研究结果及该器材仓库的实际情况，该器材的维修水平影响因子的表函数如图5所示，其中：横坐标为维修水平的模糊评价值；纵坐标为维修水平影响因子。根据陶金宸[10]的研究结果，应用模糊综合评判法得到该器材仓库的维修水平为良好，评价值为0.75，由图5可得到相应的维修水平影响因子为0.7。器材自身故障率表函数如图6所示，其中：横坐标为年份；纵坐标为自身故障率。

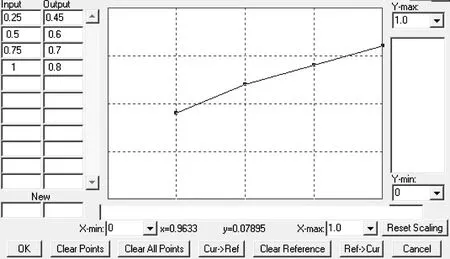
图5 XX器材维修水平影响因子表函数

图6 XX器材自身故障率表函数

器材故障率不仅与器材自身的可靠性有关，还与使用强度影响因子、运行环境影响因子和操作水平影响因子有关。因此，修正后的XX器材故障率表函数如图7所示，其中：横坐标为年份；纵坐标为器材故障率。

图7 XX器材故障率表函数

根据《中国人民解放军车辆保养规定》，车辆装备每6年进行一次大修，通常情况下，累积使用6年的器材也应进行更换[11]。因此，计算自然报废速率时，设定该器材的平均使用寿命T=6年，特征参数k=3。运用排队论方法和MATLAB软件计算第t年该器材的报废速率，则XX器材的自然完好率和相关报废速率如表3所示。其中：2016-2019年的相关数据通过双参数Weibull分布函数和排队论方法计算得出。

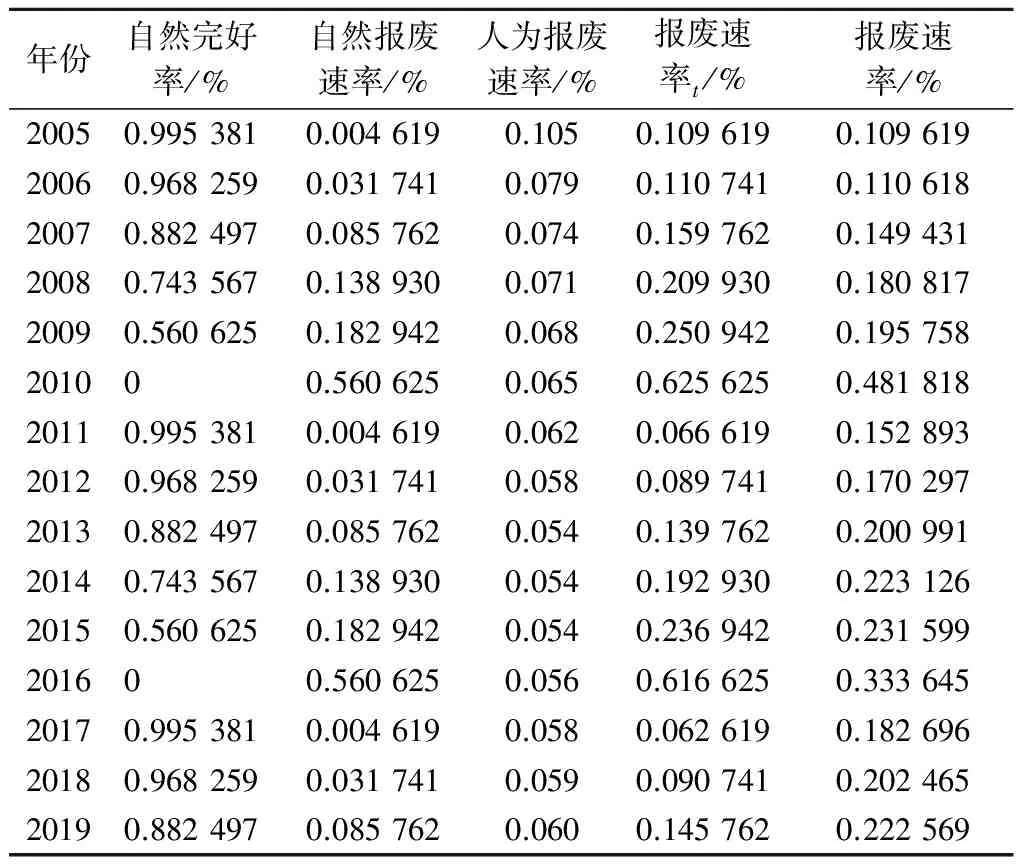
表3 XX器材的自然完好率及相关报废速率

3.2 模拟仿真

通过该器材仓库的实际需求数据和构建的数学模型方法，计算出各参数及变量的数值，应用仿真软件Vensim进行系统模型的仿真预测，具体库存需求量仿真结果如图8所示。

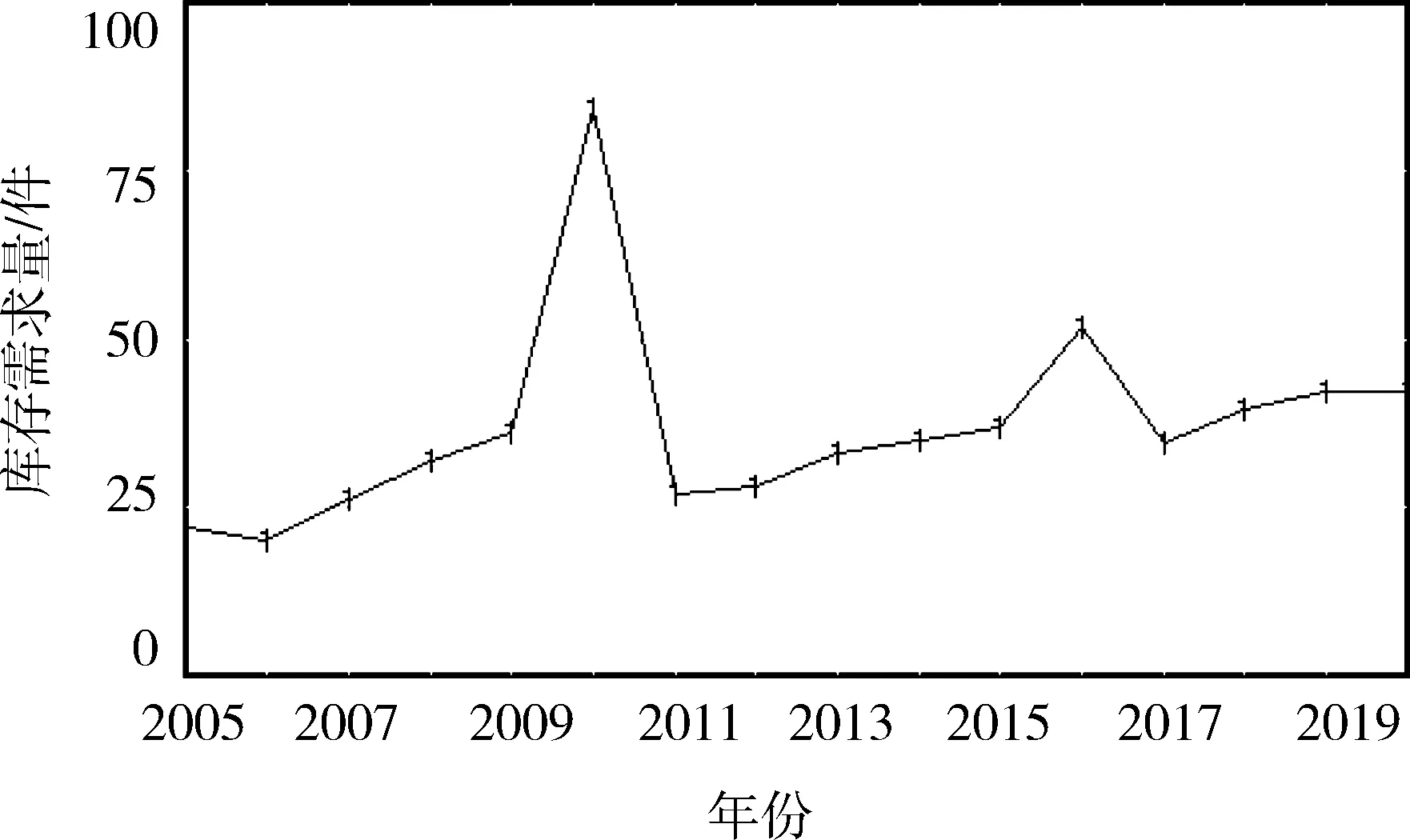
图8 XX器材库存需求量的模拟仿真结果

由图8可以看出：1)该器材库存需求量每隔6年会发生突增，这是由于笔者设定器材的使用寿命T=6年，器材累积工作6年时必须进行更换。2)该器材库存需求量基本呈上升趋势，这是由于军事训练、演习等任务不断增多，车辆装备的使用强度和发生故障的概率随之增加，库存需求量也随之增大。

车辆器材库存需求量预测系统动力学模型的仿真预测值与实际需求量对比如图9所示。系统动力学模型仿真预测结果及相对误差如表4所示。

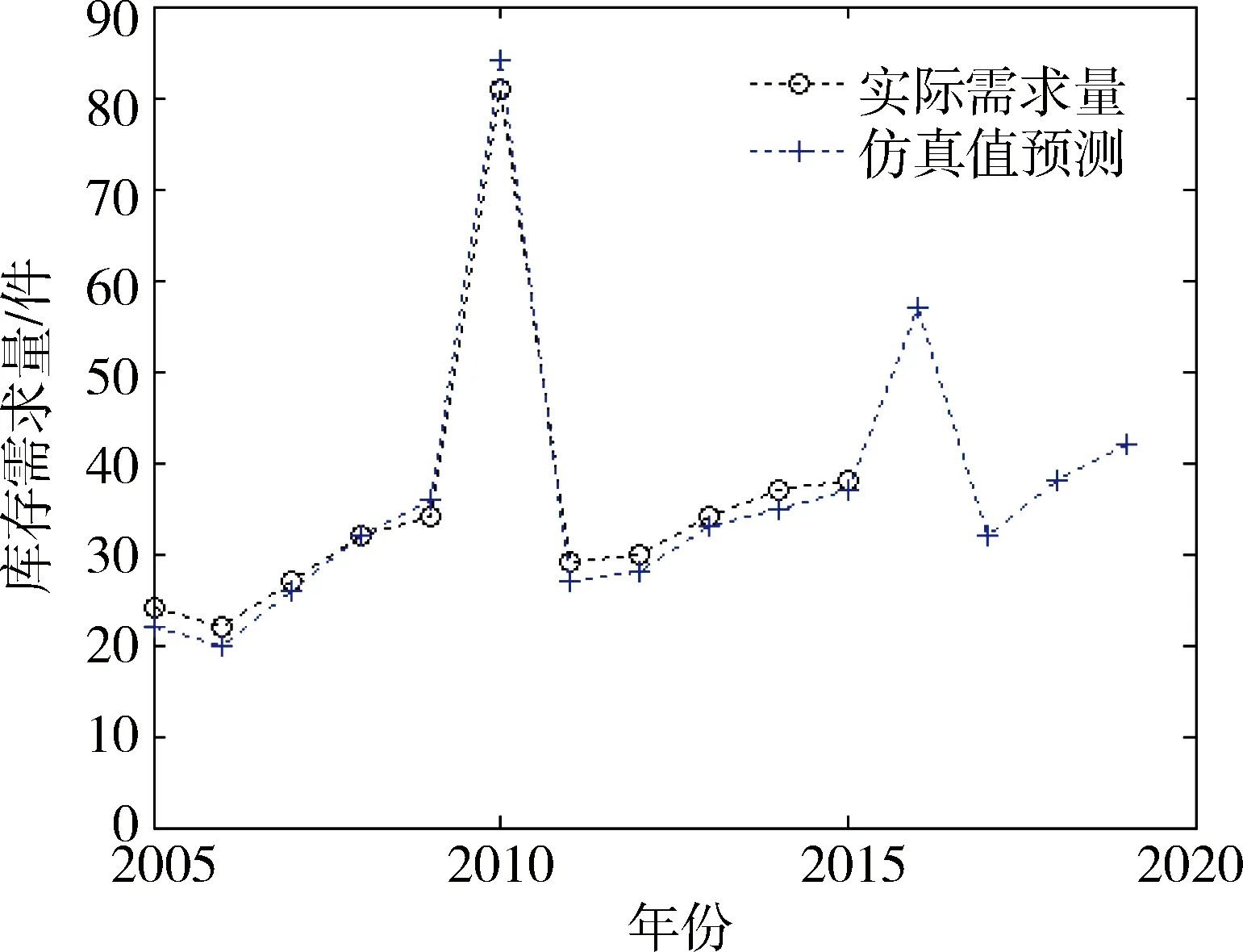
图9 库存需求量系统动力学模型仿真预测值与实际需求量对比

表4 系统动力学模型仿真预测结果及相对误差

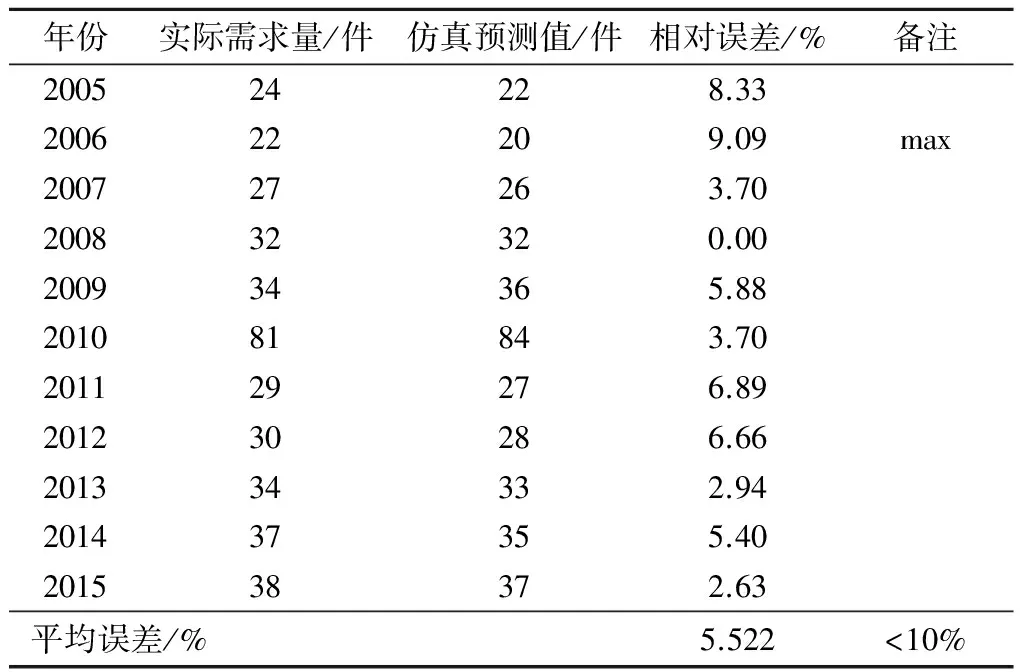
年份实际需求量/件仿真预测值/件相对误差/%备注200524228．33200622209．09max200727263．70200832320．00200934365．88201081843．70201129276．89201230286．66201334332．94201437355．40201538372．63平均误差/%5．522<10%

由表4可以看出：仿真预测值与实际需求量的最大误差为9.09%(<10%)，表明所建立的库存需求量预测系统动力学模型的预测精度达到要求，可用于部队车辆器材的库存需求量预测。运用该模型对2016-2019年的库存需求量进行仿真预测，结果分别为57、32、38、42件。

4 结论

笔者构建的模型不仅考虑了外部使用环境、器材自身故障率等因素，而且通过表函数计算了车辆装备数量增长率等不易确定的变量，有效地弥补了传统预测方法考虑影响因素较少、预测精度偏低的不足。

结合某器材仓库的实际需求数据进行了仿真预测，并将得到的仿真预测值和实际需求量进行了对比，结果表明：相对误差满足精度要求，验证了预测模型的有效性，为车辆器材库存需求量预测提供了新方法。最后，对该仓库2016-2019年XX器材的库存需求量进行了预测，为部队车辆器材筹措及库存管理提供了支撑。下一步将进一步研究各参数对所建模型的影响程度(即灵敏度)。

[1] 王亮． 军用车辆器材保障概论[M]． 北京： 金盾出版社， 2014： 9-13．

[2] 徐飞， 杨士英， 魏祥生． 基于改进灰色预测模型的雷达备件消耗预测[J]． 雷达科学与技术， 2015， 12(6)： 609-614．

[3] 罗晓萌， 李建斌， 胡鹏． 基于时间序列预测的电子商务库存优化策略[J]． 系统工程， 2014， 6(6)： 91-98．

[4] 楼增龙， 陈海松， 贺伟雄，等． 基于多元线性回归的维修器材消耗预测[J]． 装备制造技术， 2014， 28(6)： 94-96．

[5] 富盛． 基于系统动力学的乘用车保有量和报废量的预测模型研究[D]． 武汉： 武汉理工大学，2014．

[6] 王晚香．铁路客运量的系统动力学预测[J]． 大连交通大学学报， 2014， 35(5)： 10-12，16．

[7] 唐旭， 张宝生， 邓红梅，等． 基于系统动力学的中国石油产量预测分析[J]． 系统工程理论与实践， 2010， 30(2)： 207-212．

[8] 许长新， 严以新， 张萍． 基于系统动力学的港口吞吐量预测模型[J]． 水运工程， 2006， 5(5)： 26-28，40．

[9] 张鹏， 葛婷． 基于系统动力学的航材库存管理策略研究[J]． 测控技术， 2013， 32(11)： 135-138．

[10] 陶金宸． 部队车辆周转器材库存结构调整研究[D]． 天津： 军事交通学院， 2014．

[11] 王云鹏， 杨志发， 李世武． 基于系统动力学的道路运输量预测模型[J]． 吉林大学学报， 2005， 35 (4)： 426-430．

(责任编辑: 王生凤)

Vehicle Material Inventory Demand Forecast Based on System Dynamics

HE Jian1, ZHANG Da-peng2, WEN Zheng-zhong1

(1.Brigade of Postgraduate Management, Academy of Military Transportation, Tianjin 300161, China; 2. Department of Military Vehicles, Academy of Military Transportation, Tianjin 300161, China)

In view of the problems of incomplete consinderation of influence factors and low accuracy of the vehicle material inventory demand forecast, the main factors affecting the inventory demand and the causal relationship between the variables are analyzed, and a system dynamics model of the vehicle material inventory demand forecast is set up. Examples are verified and the results show that this model considers factors completely and results are closer to the actual, which has reference and application value, and it proposes a new method of scientifically forecasting the inventory demand.

vehicle material; system dynamics model; inventory demand forecast

1672-1497(2016)05-0025-06

2016-08-24

何 健(1991-)，男，硕士研究生。

E92

A

10.3969/j.issn.1672-1497.2016.05.005