基于因子分析建立综合评价模型的一种改进

黄毅茗

(广东外语外贸大学经济贸易学院，广东广州 510006)



基于因子分析建立综合评价模型的一种改进

黄毅茗

(广东外语外贸大学经济贸易学院，广东广州 510006)

[摘要]本文针对现时因子分析应用于综合评价模型中存在的问题，提出了一个结合因子分析和熵值法的改进模型，并对新模型进行了例证效度分析。分析结果表明，新模型不但保留了因子分析对信息浓缩的作用，对原信息的综合能力亦有所提升，并且其评分计算的过程体现出较高的客观性。

[关键词]因子分析；综合评价；熵值法；Spearman相关系数

1研究背景

因子分析是多元统计分析中一种重要的降维方法，其数学模型可表示为

X=μ+A·F+ε.

(1)

其中，X为变量矩阵，A为因子载荷矩阵，F为公因子矩阵，μ为变量均值向量，ε为特殊因子向量。

因子分析应用于综合评价中的优势，一是其通过降维实现了较大限度的信息浓缩，从而大大降低了信息处理成本；二是配合因子旋转其在信息降维后生成的因子具有更合理的解释。因此，因子分析被广泛应用于建立综合评价模型。其中，最常见的一种应用方式是利用因子分析方法建立如下综合评价模型：

S0=F·a.

(2)

其中，得分向量s0中的元素si为第i个被评项目的得分；F与模型(1)中同义；权重向量a中的元素aj=λj/∑λp，λj为第j个公因子fj的方差贡献率，∑λp为所有公因子的累积方差贡献率。

主成分分析亦有与模型(2)非常相似的一种应用。然而，该模型遭到了很多学者的质疑。其中，阎慈琳(1998)和王学民(2007)均认为，这种建模方法一方面缺乏数理依据，另一方面通过几个主成分的线性组合所建立的评价模型破坏了主成分在数据变异性上的优势；王学民(2007)更证明了s0的信息量与第一主成分非常接近，因此s0并未能起到综合所有主成分的作用，从而认为与其通过评价模型计算s0倒不如直接使用第一主成分进行排序更有说服力。另外，通过陈述云(1995)的说明亦可推断出，模型(2)与直接使用第一主成分作为综合评价相比，前者只是对后者在各主成分赋权上作了主观调整，其主要信息依然由第一主成分提供，并且其对各主成分信息的“综合能力”并未通过理论或实证分析的检验。

尽管如此，上述三位学者均未否定主成分分析或因子分析方法在综合评价应用中的优势。例如，王学民(2004)就利用因子分析方法对股票进行综合评价，可惜该文并未提出可供复刻的数学模型，而是通过目测的方法对各因子进行了“综合运用”。笔者认为尽管目测方法是可行的，但该方法对信息的利用程度是因人而异的，其影响因素也是主观的，因此其综合评价效果也是难以衡量的。

孙刘平(2009)就上述主成分分析应用于综合评价中的问题对该应用进行了改进，其方法是：先对原始数据进行均值化预处理，然后进行主成分分析，并利用熵值法对第一主成分没有显著贡献的指标计算出一个综合得分值，再把该得分值与第一主成分得分求均值，最后把该均值作为综合评分。这种方法在出发点上充分重视了第一主成分并顾及了其他主成分在综合评价中所起的作用，但笔者认为其仍存在以下问题：一是未能提出一个第一主成分得分与熵值法得分间的合理权重分配；二是未能发挥主成分分析降维的优势，反而使评分方法变得更复杂；三是熵值法的引入亦未提出合理的解释，笔者认为如其对余下变量指标用熵值法计算综合评分，而不如直接用第二主成分得分代替更为适合，至少两个主成分得分在数值上更具一致性及可比性。因此，笔者认为这种方法的改进效果有待考究。

因子分析在综合评价应用中主要优势在于其对信息的“简化”，即既简化了数据的输出又简化了指标变量的解释。它在综合评价建模中发挥的作用，一是根据变量间的相关关系对变量进行了分类，并配合因子旋转使类间距离达到最大；二是根据分类结果对数据进行了降维，并给出了因子得分，予综合评价模型以变量支持。以保持该优势为出发点，本文针对上述模型(2)存在的问题，利用因子分析结合熵值法建立一个改进的模型，并给出算例利用Spearman相关系数对比检验新旧模型的综合评价能力。

2改进的综合评价模型

如前所述，由于模型(2)只是各公因子的简单线性组合，而且王学民(2007)证明了模型(2)中第一因子f1的系数远比其它因子要大，因此协方差矩阵Var(s0)中的信息主要由f1提供，导致模型(2)未能解决直接把f1作为评分时可能出现的以偏概全问题。

为保持因子分析的方法优势，对模型(2)的改进应着重于权重向量的调整，并使新模型包含更多其它因子的信息。根据这一思路，新模型的权重向量应包含公因子的信息，故建立如下模型：

s=F·w.

(3)

其中，得分向量s模型(2)中的s0意义相同；F为公因子矩阵，据前面分析，F中的因子应已经过以方差最大化准则的因子旋转；权数向量w中的元素wi=wj(f1,f2,…,fp)，表示wi包含了公因子的信息，则有

Var(s)=Var(F·w)=E[Fw-E(Fw)][Fw-E(Fw)]′.

(4)

若设f*=F·w，则

Var(s)=Var(f*)=E(f*f*′)

(5)

由式(5)可知，模型(3)中s所包含的信息量取决于f*，而当F已确定时，f*包含的信息又取决于权重函数wj(f1,f2,…,fp)的选取，而非任一公因子。故模型(3)中s包含的信息不同于模型(2)中的s0，亦不同于任一公因子，其对各公因子的综合能力将依靠权重函数的选取。

3权重向量w的构造——以熵值法为例

据上描述，模型(3)对各公因子的综合能力依靠权重函数的选取，故权重函数的选取应服务于综合评价的目标。此处，本文选取一种客观赋权的方法构造w——熵值法。根据熵值法的基本原理，它通过各公因子中元素的信息量大小确定权重，实际上通过赋予区分度大的因子较高权重、区分度小的因子较低权重，从而拉开了各被评项目的得分差距。

熵值法是一种根据各项指标观测值所提供的信息量的大小来确定指标权数的方法。熵是热力学中的一个名词，在信息论中又称为平均信息量，它是信息的一个度量，仍称为熵。根据信息论的定义，在一个信息通道中传输的信号i的信息量Ii为

(6)

其中，pi是信号i出现的概率。则定义多个信号的平均信息量——熵为-∑piIi。由于熵是基于概率定义的，而概率的取值范围为[0,1]，因此在对公因子利用熵值法求权重系数前需对数据进行极差标准化。熵值法求公因子权重系数的具体步骤如下。

3.1数据预处理——极差标准化

(7)

其中，fij为第j个被评项目第i个公因子的因子得分，min(fij)表示fij中的最小值，max(fij)表示fij中的最大值。

3.2计算第i个公因子下第j个被评项目的特征比重

(8)

3.3计算第i个公因子的熵值

(9)

其中，Iij的计算见等式(6)。

3.4计算第i个公因子的权重

(10)

4例证

本文利用改进的基于因子分析的综合评价模型建模方法，建立现役美国高校橄榄球教练员的综合评价模型。对收集到的118位现役教练员11项指标数据利用SPSS 19.0进行因子分析，该11项指标具体为：岗位工资(paySchool，美元)、绩效奖金(payBonus，美元)、其它收入(payOther，美元)、执教年资(yrs，年)、参赛总场数(allGames，场)、获胜总场数(allWins，场)、战败总场数(allLoses，场)、获胜率(allPCT，%)、联赛参赛场数(bowlGames，场)、联赛获胜场数(bowlWins，场)、联赛获胜率(bowlPCT，%)。

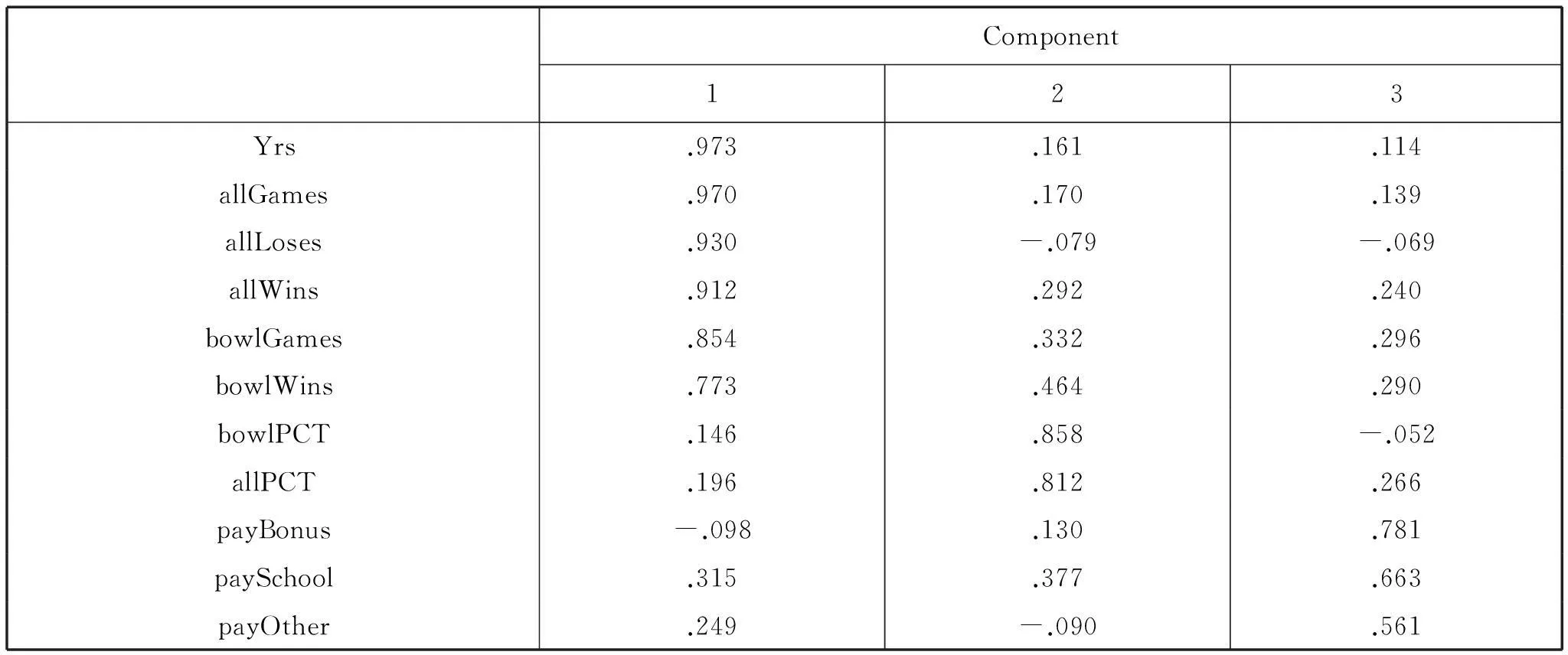
首先，对所选11项指标数据进行KMO检验和Bartlett球体检验，结果如表1所示。其中KMO的值为0.73，Bartlett球体检验的p值为0.000<0.05，认为比较适合进行因子分析。再选取主成分分析法为萃取公因子的方法，选取公因子的准则为特征值大于1，并选取因子旋转的准则为方差最大化正交旋转，运行结果的方差贡献率如表2所示，旋转后的因子载荷矩阵如表3所示。可知根据特征值与方差百分比确定3个公因子，且这3个公因子累计方差百分比达到80.73%，概括了教练员各项主要指标的大部分信息，故认为除这3个因子以外的其它变量对方差影响很小，因此把美国高校橄榄球教练员排名模型分成了3个因子。各指标的因子得分系数矩阵如表4所示。

表1　KMO and Bartlett’s Test

从表3中可知，执教年资、参赛总场数、获胜总场数、战败总场数、联赛参赛场数、联赛获胜场数6项指标在第一公因子上有较大的正载荷，故该因子可解释为经验因子。获胜率和联赛获胜率两项指标在第二公因子上有较大的正载荷，故该因子可解释为获胜因子。岗位工资、绩效奖金和其它收入3项指标在第三公因子上有较大的正载荷，故该因子可解释为薪酬因子。

最后，根据表4中的因子得分系数矩阵计算因子得分矩阵F，并利用F根据模型(3)及等式(7)至(10)计算出118位美国现役橄榄球教练员的综合评价模型为

s=0.37f1+0.27f2+0.36f3.　(11)

Extraction Method: Principal Component Analysis.

Rotation Method: Varimax with Kaiser Normalization.

a.Rotation converged in 4 iterations.

表4　Component Score Coefficient Matrix

Extraction Method: Principal Component Analysis.

Rotation Method: Varimax with Kaiser Normalization.

根据模型(11)计算出了118位教练员的综合评分(记为s)。为进行模型的效度分析及对比，亦按照模型(2)计算出了118位教练员的综合评分(记为s0)，并把s、s0以及直接把第一因子的因子得分作为综合评分(记为f1)三者与11项指标变量的Spearman相关系数进行比较(表5)。Spearman相关系数描述两个变量之间的关联程度与方向的等级相关，适用于总体分布类型未知的数据。

根据表5中的数据，s与11项的Spearman相关系数都通过了显著性检验(p值<0.05)，但s0和f1均与部分变量的Spearman相关系数未能通过显著性检验。结果说明，一是s与原信息所有变量都是显著相关的，例证结果表明的s对原信息有一定的综合能力；二是s0和f1的评分结果是有较严重偏颇的，未能充分利用原数据对研究对象进行较好的综合评价。

表5　Spearman’s rho Correlations

5结论

本文针对现时因子分析应用于综合评价模型中存在的问题，提出了一个结合因子分析和熵值法的改进模型，并对新模型利用118位美国高校橄榄球教练员的数据进行了例证分析，与现时两种常用综合评价模型的结果进行了效度对比。例证分析结果表明，新模型不但保留了因子分析对信息浓缩的作用，而且对原信息的综合能力亦较旧方法佳，其评分计算的过程亦表现出较高的客观性。

[参考文献]

[1]阎慈琳.关于用主成分分析做综合评价的若干问题[J].数理统计与管理,1998(2):22-25.

[2]王学民.对主成分分析中综合得分方法的质疑[J].统计与决策,2007(8):31-32.

[3]陈述云.对多指标综合评价的主成分分析方法的改进[J].统计研究,1995(1):35-39.

[4]王学民.因子分析在股票评价中的应用[J].数理统计与管理,2004(3):6-10.

[5]孙刘平.基于主成分分析法的综合评价方法的改进[J].数学的实践与认识,2009(18):15-20.

[6]郭亚军.综合评价理论、方法及应用[M].北京:科学出版社,2007.

[7]Richard A.Johnson,Dean W.Wichern.实用多元统计分析[M].陆璇,译,北京:清华大学出版社,2001.

[8]王学民.应用多元分析[M].上海:上海财经大学出版社,2004.

[作者简介]黄毅茗(1987- )，女，硕士研究生，从事经济数学模型分析与应用研究。

[收稿日期]2015-12-13

[中图分类号]O213

[文献标识码]A

[文章编号]2095-7602(2016)02-0014-05