图上的p-Laplacian方程解的性质及其数值仿真

王　坤，辛　巧

(伊犁师范学院数学与系统科学学院，新疆伊宁 835000)



图上的p-Laplacian方程解的性质及其数值仿真

王坤，辛巧

(伊犁师范学院数学与系统科学学院，新疆伊宁 835000)

[摘要]本文通过研究图上的p-Laplacian算子的基本性质，首先讨论了图上的p-Laplacian方程解的性质；其次，给出了一个图上的p-Laplacian方程的解析解论证了理论上的结果；最后，对另一个图上的p-Laplacian方程进行数值模拟验证理论上的结果。

[关键词]图上的p-Laplacian算子；图上的p-Laplacian方程；Cauchy问题

图(Graph)通过一些有意义的连接(边)表示离散对象的相互关系，它是计算机科学、生物学、经济学、社会学等领域用来分析离散对象关系的重要工具.近年来，图谱理论是讨论图的识别问题的重要工具之一.2005年，Berenstein和Chung[1]对定义在图上的函数引入了积分、方向导数、梯度、离散Laplacian算子等概念，并利用图上的调和方程的反问题讨论图的边的连通性和连接权重的识别问题.2007年，S.Y. Chung、Y.S. Chung和J.H. Kim[2]引入了图上的ω-热方程，讨论了其初值和边值问题的可解性，利用ω-扩散核的概念刻画了其解的形式.2008年，Elmoataz、Lezoray和Bougleux[3]从图上的能量泛函的极小化出发，引入了图上的p-Laplacian算子，并将其应用于图像去噪问题.此外，图上的偏微分方程还可进一步应用于分子扰动分析[4]、动力系统[5]、图像分割[6]等研究领域.2012年，Y.S. Lee和S.Y. Chung[7]讨论了带有狄利克雷边界条件的图上的p-Laplacian方程初边值问题解的熄灭和正性.在本文中，我们主要讨论图上的p-Laplacian方程Cauchy问题(也称为初值问题)解的性质，该结果推广了文献[8]中关于非局部热方程解的性质的研究.值得注意的是，文献[3]和[7]中关于离散的p-Laplacian算子的定义略有差异，我们采用文献[3]中p-Laplacian算子的定义.

1预备知识

首先，给出一些图论中的基本符号、定义以及图上的函数的积分、方向导数、梯度和离散p-Laplacian算子及其伴随算子[1,3,9]. 在下文中，G(V，E，ω)通常表示简单、连通赋权图，其中有限集合V表示图G顶点，用符号x∈V表示x是图G的顶点，而E⊂V×V表示其赋权边的集合，用符号x~y表示图G中连接顶点x和y的边，边的权重函数定义为：ω：V×V→[0，+∞)，且满足：(1)对任意的x∈V，有ω(x，x)=0；(2)若x~y，则ω(x，y)=ω(y，x)>0，即对称性、非负性；(3)如果E中不存在连接顶点x和y的边，则ω(x，y)=0.

图G(V，E，ω)上的函数可以理解为定义在图顶点集合V上的映射u：V→R，类似于连续函数空间上积分的定义，其在图G上的积分定义如下：

方向导数为

ωu(x)=(dω，yu(x))y∈V.

在下文中，用符号H(V)表示定义在图G(V，E，ω)顶点集V上的函数的集合，对于任意的u(x)，v(x)∈H(V)，其内积定义为

〈u(x)，v(x)〉H(V)=∫Vu(x)v(x).

容易验证H(V)为Hilbert空间.类似地，用符号H(E)表示定义在图G(V，E，ω)边集E的函数U∶(x，y)→R的集合，对任意的U(x，y)，V(x，y)∈H(E)，定义它们的内积为

也容易验证该空间为Hilbert空间.

在上述基本定义的基础上，方向导数的伴随算子记作d*∶H(E)→H(V)(线性算子)的定义为

〈du，U〉H(E)=〈u，d*U〉H(V).

此外，其详细的计算公式

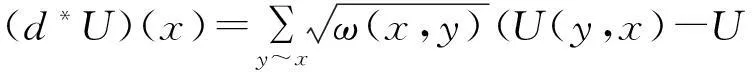
证明可参考文献[5]的推论1.

根据伴随算子的定义进行计算，容易知

其中，γ(x，y)=|ωu(x)|p-2+|ωu(y)|p-2，具体的证明细节可以参考文献[5]的推论3.

2主要结果

在研究图上的p-laplacian方程Cauchy问题解的性质之前，先给出离散的p-laplacian算子的性质，有如下定理.

证明(a)由于u(x)恒为常数，所以对于∀x，y∈V都有u(x)=C(C为常数)，进而u(x)-u(y)=0，再由离散的p-laplacian算子的定义可知

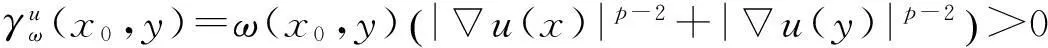
(b)若∃x0∈V，对∀x∈V，有u(x0)≥u(x)，由于

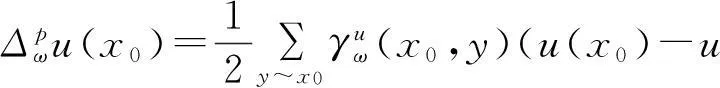
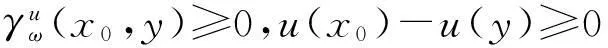
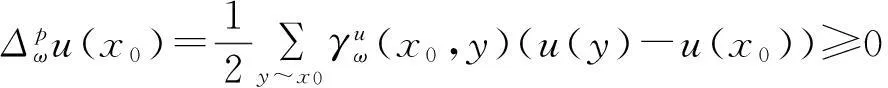
(c)根据离散的p-laplacian算子的定义、权重函数ω(x，y)的对称性和函数空间H(V)内积的定义，可得到

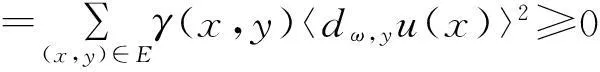
(d)

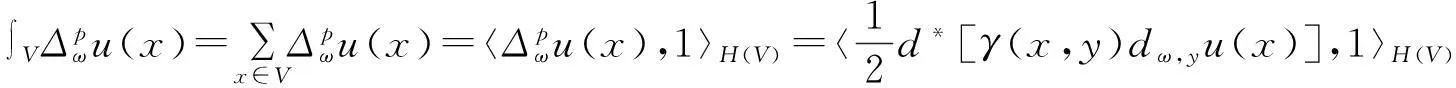
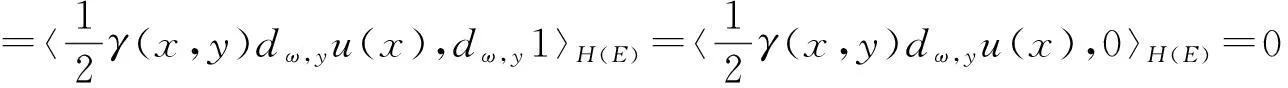
在研究上述离散的p-laplacian算子性质的基础上，可得到如下图上离散的p-laplacian方程Cauchy问题解的性质.

目前中国的餐饮企业核心特征为虽然客户群体庞大，发展前景很乐观，但整个餐饮业发展阶段足够丰富，即每家企业所处的发展阶段存在很大差别，龙头企业相对稀缺，在上市企业中也毫无存在感！国内大部分餐饮企业发展遇到瓶颈！

定理2图上离散的p-laplacian方程的Cauchy问题：

(1)

证明(ⅰ)由离散的p-laplacian算子的性质(d)，则有

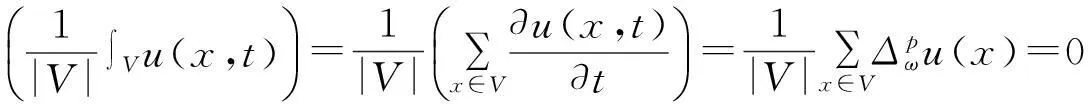
(ⅱ)若存在顶点x0∈V，对于∀x，u(x0，t)是方程的解u(x，t)的最大值，那么

类似地，对于任意的顶点x0∈V，若u(x0，t)是方程的解u(x，t)的最小值，那么

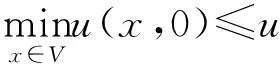
(ⅲ)对于能量函数E(t)，有

=-〈u(x，t)，d*[γ(x，y)dω，yu(x，t)]〉H(V)

=-〈dω，yu(x，t)，γ(x，y)dω，yu(x，t)〉H(E)

≤0.

3数值模拟

下面我们给出两个具体的实例用于论证理论上的结果.

例1设图G(V，E，ω)为2个顶点的完全图，V={x1，x2}，特别选取ω=1(此时，该图称为标准图)，则该图上的p-Laplacian方程(1)可以具体表示为：

(2)

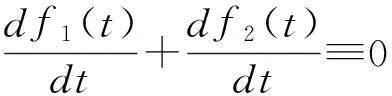
由(2)的两个方程和0

当p≠2时，解析解为

当p=2时，解析解为

不管p取何值，都容易验证方程(2)的解满足定理2.

例2设图G(V，E，ω)为3个顶点的完全图，V={x1，x2，x3}，也特别选取ω(xi，xj)=1，1≤i≠j≤3，则该图上的p-Laplacian方程(1)可以具体表示为

(3)

其中，c1，c2，c3为常数，f1(t)，f2(t)，f3(t)分别是f(x1,t),f(x2,t),f(x3,t)的简单表示，fi在各个顶点的梯度算子的模定义如下：

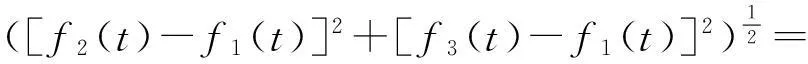
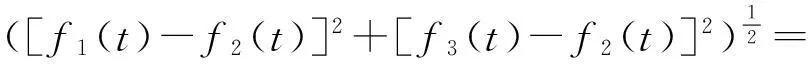
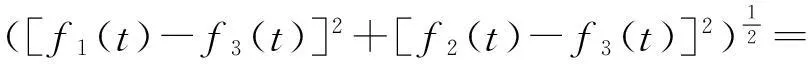
由于微分方程组(3)的非线性，不容易求其解析解.在此，我们考虑它的数值解，对时间变量采取显式的差分格式.在下面的数值模拟中，Δt为时间步长设定为0.001，p=2.5，c1=15,c2=8,c3=2.8.在图1中，实的曲线为函数f1(t)，点状的曲线为f2(t)，虚线短表示的曲线为f3(t)，可见当时间t足够大时，三者的值都收敛到初值的平均值.定理2(c)中的能量函数E(t)随时间递减，其函数图像如图2所示.

图1　解的数值模拟

图2　能量函数的图像

4结论

本文主要考虑了图上的p-Laplacian算子及图上的p-Laplacian方程Cauchy问题解的性质，并且给出了两个实例用于进一步论证理论上的结果.由定理2和定理3的结果得到离散的p-laplacian方程确实可用于图像去噪，并且具有一些好的性质，其在文献[3]中也得到了印证.在后续的研究过程中，我们可以进一步讨论其在图像处理问题中的其它应用.

[参考文献]

[1]Chung S Y,Berenstein C A.ω-Harmonic function and inverse conductivity problems on networks[J].SIAM J Appl Math,2005,56(4):1200-1226.

[2]Chung S Y,Chung Y S,Kim J H.Diffusion and elastic equations on networks[J].Publ Res Inst Math Sci,2007,43(3): 699-725.

[3]Elmoataz A,Lezoray O,Bougleux S.Nonlocal discrete regularization on weighted graphs:a framework for image and manifold processing[J].IEEE Tans Image Process,2008,17(7):1047-1060.

[4]Trinajstic N,Babic D,Nikoli S.The Laplacian matrix in chemistry[J].J Chem Inf Comput Sci,1994,34(2):368-376.

[5]Zakrzewski W J.Laplacians on lattices[J].J Nonlinear Math Phys,2005,12(4):530-538.

[6]Ta V T,Lezoray O,Elmoataz A, et al.Graph-based tools for microscopic cellular image segmentation[J].Pattern Recognition,2009,42(6):1113-1125.

[7]Lee Y S,Chung S Y.Extinction and positivity of solutions of the p-Laplacian evolution equation on networks[J].J Math Anal Appl,2012,386(2):581-592.

[8]Gilboa G,Osher S.Nonlocal linear Image regularization and supervised segmentation[J].Multiscale Model Simul, 2007,6(2):595-630.

[9]辛巧,许璐,王安平.无限图上带吸收项的热方程解的熄灭和正性[J].云南大学学报:自然科学版,2013,35(6):727-730.

Properties of the Solution for the p-Laplacian Equation on Graphs and Its Numerical Simulation

WANG Kun, XIN Qiao

(College of Mathematics and Statistics, Yili Normal Univeristy, Yining Xinjiang 835000, China)

Abstract:Throughout the researches on the basic properties of the p-Laplacian operator, the properties of the solution for the p-Laplacian equation on graphs were considered. Finally, the analytic solution of an example for the p-Laplacian equation on a special graph is used to demonstrate the theoretical results. Furthermore, the numerical simulation for the p-Laplacian equation on a complex graph is given.

Key words:p-Laplacian operator on graphs; p-Laplacian equation on graphs; Cauchy problem

[通讯作者]辛巧(1981- )，男，副教授，博士，硕士生导师，从事偏微分方程及应用研究。

[作者简介]王坤(1991- )，男，硕士研究生，从事偏微分方程及应用研究。

[基金项目]新疆维吾尔自治区自然科学基金项目“图上的偏微分方程解的性质研究”(201442137-30)；伊犁师范学院2014年度研究生科研创新项目“图上的偏微分方程解的渐进行为”(2014YSY022)。

[收稿日期]2015-10-16

[中图分类号]O175.29

[文献标识码]A

[文章编号]2095-7602(2016)02-0009-05