线性齐次Q周期系数系统的Floquet理论

曲婧佳，商玉凤

(空军航空大学基础部，吉林长春 130022)



线性齐次Q周期系数系统的Floquet理论

曲婧佳，商玉凤

(空军航空大学基础部，吉林长春 130022)

[摘要]本文介绍了线性齐次周期系数系统的Floquet理论，在此基础上进一步推导出线性齐次Q周期系数系统的Floquet理论。

[关键词]线性齐次周期系数系统；线性齐次Q周期系数系统；Floquet理论

1线性齐次周期系数系统的Floquet理论

考虑线性齐次周期系数系统

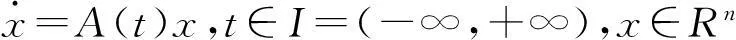
(1)

其中，A(t)是在(-∞，+∞)上连续且以T(T>0)为周期的n×n矩阵函数，满足A(t+T)=A(t).

定理1在变换x=H(t)y之下，系统(1)可化为线性齐次常数系统

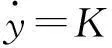
其中，K=T-1lnD，设Φ(t)是系统(1)的一个基本解矩阵，D为使得Φ(t+T)=Φ(t)D的常值矩阵，H(t)=Φ(t)e-tK.

2线性齐次Q周期系数系统的Floquet理论

下面考虑线性齐次Q周期系数系统

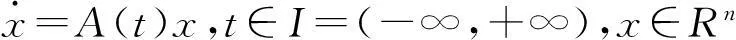
(2)

其中，A(t)是在(-∞，+∞)上连续的n×n矩阵函数，且满足A(t+T)Q=QA(t)，T>0，Q为可逆常值矩阵.

定理2设Φ(t)是系统(2)的一个基本解矩阵，则Q-1Φ(t+T)也是系统(2)的基本解矩阵，此外，对于每个Φ(t)，存在一个可微且满足P(t+T)=QP(t)的非奇异矩阵函数P(t)，以及一个常值矩阵R使得

Φ(t)=P(t)etRQ.

证明记Ψ(t)=Q-1Φ(t+T)，t∈(-∞，+∞).因为

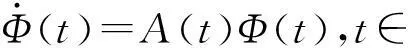
所以Ψ(t)满足

=Q-1QA(t)Q-1Φ(t+T)=A(t)Q-1Φ(t+T)

=A(t)Ψ(t)，t∈(-∞，+∞).

此外，由于对于一切t∈(-∞，+∞)，detΦ(t)≠0，故detΨ(t)=det(Q-1Φ(t+T))≠0，所以Ψ(t)=Q-1

Φ(t+T)系统(2)的一个基本解矩阵.

因此，Φ(t)与Ψ(t)只相差一个非奇异矩阵C，Q-1Φ(t+T)=Φ(t)C，且存在一个常值矩阵R使得C=eTRQ，即有

R=T-1[lnC]Q-1.

(3)

令

P(t)=Φ(t)e-tRQ.

(4)

因为Φ(t)是系统(2)的一个基本解矩阵，所以它对一切t∈(-∞，+∞)都是非奇异的和可微的，e-tRQ对于一切t∈(-∞，+∞)也都是非奇异的和可微的，所以P(t)也是非奇异的和可微的.此外

P(t+T)=Φ(t+T)e-(t+T)RQ=QΦ(t)Ce-(t+T)RQ=QΦ(t)eTRQe-(t+T)RQ=QΦ(t)e-tRQ=QP(t).

由(4)得到结论

Φ(t)=P(t)etRQ.

对于系统(2)有类似定理1的结论.

定理3系统(2)在变换x=P(t)y之下，可化为线性齐次常数系统

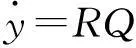
(5)

其中，R和P(t)分别由(3)和(4)给出.

证明x=P(t)y，两边对t求导，得到

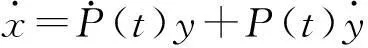
由于x满足系统(2)，故有

从而

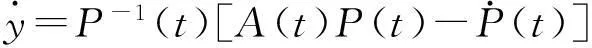
(6)

利用(4)，并考虑到Φ(t)是系统(2)的一个基本解矩阵，可知

=A(t)Φ(t)e-tRQ-A(t)Φ(t)e-tRQ+Φ(t)RQe-tRQ

=Φ(t)e-tRQRQ

=P(t)RQ.

(7)

将(7)代入(6)，即得(5).

[参考文献]

[1]陆启韶,彭临平,杨卓琴.常微分方程与动力系统[M].北京:北京航空航天大学出版社,2010.

[2]韩茂安.动力系统的周期解与分支理论[M].北京:科学出版社,2002.

[3]伍卓群,李勇.常微分方程[M].北京:高等教育出版社,2004.

The Floquet Theory of Linear Homogeneous Q Periodic Coefficient System

QU Jing-jia，SHANG Yu-feng

(Fundamental Department, Aviation University of Air Force, Changchun Jilin 130022, China)

Abstract:In this paper, we introduced the Floquet theory of linear homogeneous periodic coefficient system, then deduced Floquet theory of linear homogeneous Q periodic coefficient system.

Key words:linear homogeneous periodic coefficient system;linear homogeneous Q periodic coefficient system; Floquet theory

[作者简介]曲婧佳(1986- )，女，讲师，硕士，从事常微分方程研究。

[收稿日期]2015-10-11

[中图分类号]O175

[文献标识码]A

[文章编号]2095-7602(2016)02-0007-02