基于模态分析的印制电路板抗振优化设计

周嘉诚，刘 芳

（武汉纺织大学 机械工程与自动化学院，湖北 武汉 430073）

基于模态分析的印制电路板抗振优化设计

周嘉诚，刘 芳

（武汉纺织大学 机械工程与自动化学院，湖北 武汉 430073）

在无人机内狭小空间和振动环境下，利用ANSYS有限元软件建立印制电路板模型，在四周固定边界条件下对印制电路板进行模态分析，获得印制电路板的4阶固有频率和振型。基于模态分析结果，对印制电路板进行优化抗振设计。结果表明，优化设计后电路板的一阶固有频率提高了近90 Hz，找到了适合狭小空间下的提高电路板稳定性的方法。

无人机；印制电路板；有限元模型；模态分析；抗振；优化设计

随着汽车、飞机等交通工具的迅速发展，车载、机载电子设备愈来愈多。在运输和使用中，电子设备遭受振动、冲击、高温等恶劣环境影响。据相关数据统计，在引起电子类产品失效的环境因素中，振动所占的比重为20%。因此，电子产品的抗随机振动性能成为判断电子设备可靠性的重要指标之一[1]。

目前，已经有不少学者利用有限元软件对印制电路板开展模态分析[2]、随机振动分析[3]和振动特性分析，有的对印制电路板组件的包装原理和插装方式提出改良意见[4]。这些仿真模拟和实验得出的结论，为印制电路板的后续研究提出了宝贵的数据和经验。

本文研究的印制电路板应用于无人机上，利用有限元软件ANSYS建立模型，结合其约束条件确定其边界条件，开展模态分析，并基于模态分析结果对该印制电路板的结构设计进行优化。采用有限元模拟的方法能快速找到问题所在，减少产品开发周期，节约开发成本，改良设计方案，对提高印制电路板疲劳寿命有很大意义[5]。其中，对于狭小空间和振动环境下的印制电路板约束条件和抗振优化设计的仿真模拟，对今后相同情况下的设计提供了新的思路和方法。

1 实验对象与有限元模型

印制电路板和上属芯片在随机振动中主要失效形式是危险点的疲劳破坏，因此找到印制电路板和上属芯片的危险点，计算疲劳寿命，可判断是否满足疲劳要求。本文选用的印制电路板是用于无人机中的一部分电子器件，因此做该电路板的动态特性分析有重要的实际意义。

印制电路板长66 mm，宽64 mm，厚度2 mm，主芯片边长14 mm，其余芯片边长依次为5，4，3 mm，通过无铅焊点焊接到电路板上，具体情形如图 1所示。印制电路板弹性模量为1.2 GPa、泊松比为0.42，密度为950 kg/m3。芯片的弹性模量为1.07 GPa、泊松比为0.410 1，密度1 040 kg/m3。

图1 印制电路板Fig.1 Print circuit board

在利用有限元软件分析实际问题中，有限元模型建立的好坏与有限元分析结果的正确与否关系密切，因此建立一个与实际相符合的有限元模型至关重要[6]。

有限元模型见图2，该模型有28 917单元，47 424节点，模型采用的单元类型为SOLID185，该单元是用于构造三维固体结构。单元通过 8节点来定义，每个节点有3个沿着xyz方向平行的自由度。单元具有超弹性、应力刚化、蠕变、大变形和大应变能力。还可采用混合模式模拟几乎不可压缩弹塑材料和完全不可压缩超弹塑材料。该模型采用MPC约束算法建立电路板与各芯片间的关系，为了简化模型，将在引脚部分做简化处理[7]。

图2 有限元模型图Fig.2 Finite element model of PCB

2 模态分析

该印制电路板固定方式为四周固定，在有限元软件中建立模型进行，采用Block Lanczos法[8-9]进行模态分析，获得该系统前4阶的固有频率，见表1，前4阶固有振型，见图3～6。

表1 印制电路板的前4阶固有频率Tab.1 The first four inherent frequencies of PCB

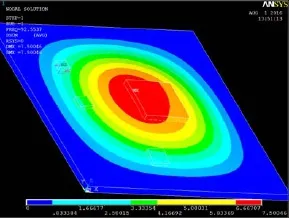
图3 一阶模态振型Fig.3 First-order mode vibrating shape

图4 二阶模态振型Fig.4 Two-order mode vibrating shape

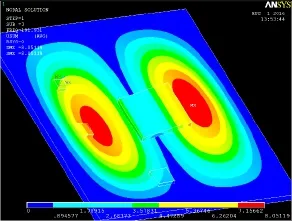
图5 三阶模态振型Fig.5 Three-order mode vibrating shape

在图中，SMX表示节点应力中的最大解，单位为 MPa，根据图中颜色变化，颜色越深表示应力越大，在图中 MX处，表示印制电路板该振型下的最大应力位置。

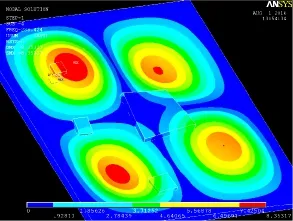
图6 四阶模态振型Fig.6 Four-order mode vibrating shape

3 防震优化设计

本文所选用的印制电路板来源于自制的无人机。无人机工作的环境复杂，受到外界干扰多，因此，提高每个印制电路板的抗振能力，保证其工作的稳定性[9]，是无人机正常运行的关键所在。

目前，印制电路板的抗振研究有一些重要结论[10]，在振动研究方面，其中 Steinberg提出了著名的Steinberg公式，即：对于四周固定的支撑的印制电路板受到外界 Z=Z0sin(fnt)的周期振动激励时，其最大振幅为式中：fn为印制电路板固有频率；Gou1为印制电路板最大振幅处的加速度，且 Gou1=GinQ，Gin为激励载荷的加速度；Q为印制电路板的激励传递率，在外界激励不变的情况下，Amax∝Gou1。因此为了降低Amax，提高印制电路板和芯片的振动疲劳寿命，必须尽量提高印制电路板的固有频率fn，特别是一阶固有频率[11]。

根据上述理论并结合无人机实际情况，本文抗振优化设计主要从两个方面考虑：

（1）对印制电路板上芯片进行保护，避免因芯片损伤造成电路板失效；

（2）提高印制电路板的固有频率，尤其是一阶固有频率，防止因共振造成电路板失效。因此本文采取以下措施。

3.1 改变芯片布局

通过前面的一阶模态振型图可以看到，主芯片相对质量和尺寸较大，且处于印制电路板变形最大位置，若发生谐振，主芯片非常容易因受力过大导致焊点断裂等原因使芯片失效。同时发现印制电路板四周及其边缘处的振幅不大，变形较小。因此，最简单有效的办法则是更改印制电路板中芯片贴装的位置，在保证芯片能够正常装贴在印制电路板的情况下，将各个芯片的位置往印制电路板的四周移动。从而提高该印制电路板的固有频率，达到提高其抗振性的效果。具体如图7所示。

图7 芯片位置移动示意图Fig.7 Change diagram of chip position

如图7，移动后芯片后，对其进行网格划分和加载，得到新模型如图 8所示。对上述模型进行模态分析，得到新系统的前4阶固有频率，如表2所示。

图8 布局改变后的模型Fig.8 Structure model after change layout

表2 优化后印制电路板的前4阶固有频率Tab.2 The first four-order natural frequencies of PCB after optimization

对比移动前后固有频率变化发现，移动后 PCB板的固有频率有所提高，但是提高的幅度不大，从第一阶模态和第四阶模态看出，改变芯片布局后固有频率整体提高了2～5 Hz。对比其他文献中的实验结果发现，之所以固有频率变化幅度不大，原因有如下两点：（1）本文选用的印制电路板偏小，大小只有64 mm×66 mm，厚度为2 mm，而普通使用在机箱或者交通设备中的印制电路板大小远大于此，电路板越大，提升效果越明显；（2）该印制电路板的材料属于普通材料范围，如选用高级设备或军用级别材料，材料性能更加优越，固有频率的提升也会更加明显。例如，一个大小238 mm×156 mm，厚度为2 mm，底部96芯接插件宽度为90 mm，材料选用FR-4 覆铜箔环氧玻璃纤维布板，经过上述类似优化后，频率能提高20～30 Hz，这就满足了优化的需要[12]。

从振型上来看，该优化后的印制电路板前 4阶振型如图9～12所示。

图9 改变芯片布局后一阶模态Fig.9 First-order mode shape after change chip position

图10 改变芯片布局后二阶模态振型Fig.10 Two-order mode shape after change chip position

图11 改变芯片布局后三阶模态振型Fig.11 Three-order mode shape after change chip position

图12 改变芯片布局后四阶模态振型Fig.12 Forth step mode shape after change chip position

从该振型图中可以发现，主芯片远离了最大变形位置，其他的小芯片也距离最大变形区域更远，这样就更好地保护了芯片，让其抗振性性和工作寿命大大提高。

3.2 增加紧固点

针对印制电路板的的薄弱环节，在该印制电路板中间增加一个支撑点，再进行模态分析，得到的固有频率见表3和前四阶模态振型图如图13～16所示。

表3 增加紧固点后的印制电路板的前4阶固有频率Tab.3 The first four-order natural frequencies of PCB after increase the fastening point

由表3与表1、表2对比可见，固有频率有所提高，特别是一阶固有频率提升尤为明显，因此结合Steingberg理论和通过增加紧固点的方式，印制电路板的抗振能力得到了显著提高。

图13 增加紧固点后一阶模态振型Fig.13 First-order mode shape after increase the fastening point

图14 增加紧固点后二阶模态振型Fig.14 Two-order mode shape after increase the fastening point

图15 增加紧固点后三阶模态振型Fig.15 Three-order mode shape after increase the fastening point

图16 增加紧固点后四阶模态振型Fig.16 Four-order mode shape after increase the fastening point

从上述振型图中可以看出，增加紧固点以后，前四阶振型图中，中间部位的振幅明显减小，最大振幅区域都往边缘移动，所有芯片都有效避开了最大形变位置，结果符合措施 1中的要求[13]。如果想要继续提高印制电路板的固有频率，可以继续增加紧固点，紧固点越多，一阶频率越高，变形量越小[13]。除去上述两种方式外，应用于其他场合的印制电路板（例如，电子机柜和电脑机箱等），还可以采用增加加强铁板或者铝板、提高加强板材料性能的办法来提高印制电路板的固有频率和改善固有振型。

4 随机疲劳计算

按照上述设计修改印制电路板后，对其运用ANSYS经行随机振动仿真，由分析结果得出最大位移处的应力值[13]。由 Miner定律的线性累积损伤理论，假定应力幅循环了 n次时，消耗了材料疲劳寿命的n/N部分，N为应力幅对应的最大循环次数，而其他应力水平的循环也以相同方式对材料产生部分损伤，累积损伤当D=1时，表示疲劳寿命已经耗尽，预测发生了疲劳破坏。考虑到该假设的不精确性和缺点，累积损伤D经常假定为一个小于1的一个数就表示疲劳已经发生。

根据ANSYS的分析结果可知，载荷步3第1子步的1σ最大Von Mises应力值为14.486 7 MPa，位置处于节点7 635处。该点的载荷步4的第1子步最大Von Mises应力值为31 848.6 MPa，即该节点处的振动平均频率为 2 198.5 Hz，假设结构振动时间t=3×105s，则有

根据经验公式σ-1=0.167σb+75=108.4 MPa。

应力等于1σ=14.487 6 MPa时，

应力等于2σ=28.973 4 MPa时，

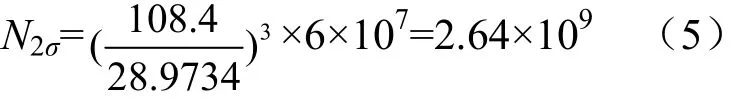
应力等于3σ=28.973 4 MPa时，

根据计算结果发现，该优化设计后的印制电路板符合疲劳要求。

5 结论

利用有限元软件对印制电路板的模态特性进行分析，基于模态分析结果开展印制电路板的抗振优化设计。在无人机的狭小环境中，通过改变印制电路板芯片布局和增加紧固点的方式，有效提高了电路板的固有频率，改善了振型，保护了芯片，因此上述两种方法在其他类似于无人机等狭小空间内的电路板设计都有很大的借鉴价值。这也为其他更加复杂的印制电路板产品的设计与开发提供借鉴，具有一定的参考价值。

[1] 高驰名. ANSYS在印制电路板组件随机振动分析中的应用 [J]. 专题技术与工程应用, 2015(7): 95-98.

[2] 李春洋. 基于模态分析的印制电路板振动可靠性研究 [J]. 中北大学学报: 自然科学版, 2007, 28: 156-160.

[3] 唐远强. ANSYS在梁-板壳结构随机振动分析中的应用 [J]. 新技术新工艺, 2009(12): 39-40.

[4] 陈元龙. 印刷电路板振动特性及防震包装原理 [J]. 包装工程, 2008(1): 10-12.

[5] 章思超. 基于有限元的驱动端盖的改进设计 [J]. 汽车电器, 2016(5): 22-24.

[6] 张洪才. ANSYS14.0理论解析与工程应用实例 [M]. 北京: 机械工业出版社, 2013.

[7] 姜青龙. 印刷电路板温度-应力耦合场有限元 [J]. 计算机科学与技术, 2009(2): 37-42.

[8] 李心洁. PCB安装结构对元器件随机振动响应的影响 [J]. 制导与引信, 2015(3): 46-49.

[9] 高军. 均匀热环境下四边固支矩形PCB薄板的自由振动 [J]. 振动与冲击, 2014, 33: 75-79.

[10] 李欣欣. 电子机柜中印制电路板的模态分析及抗振设计 [J]. 机械工程与自动化, 2007(3): 18-22.

[11] LUAN J E, TEE T Y. Modal analysis and dynamic response of board level drop test [C]//Electronics Packaging Technology Conference. NY, USA: IEEE, 2003: 233-243.

[12] 杨宇军. 插板式 PCB的内置式减振设计方法及其 PSD动力学仿真[J]. 振动与冲击, 2007(26): 39-42.

[13] WEI S B, KAO I. Vibration analysis of wire and frequency response in the modern wire saw manufacturing process [J]. J Sound Vib, 2000, 231(5): 1383-1395.

（编辑：陈渝生）

Anti-vibration optimal design of PCB based on modal analysis

ZHOU Jiacheng, LIU Fang

(Faculty of Mechanical Engineering and Automation, Wuhan Textile University, Wuhan 430073, China)

Under the condition of narrow space and vibration in unmanned aerial vehicle, a printed circuit board (PCB) model was set up by using ANSYS finite element software, and the modal analysis was proceeded with around the fixed boundary condition. The 4-steps natural frequencies and vibration mode were obtained, and the optimized anti-vibration design of the PCB was conducted. The results show that the first four-order natural frequency is increased by about 90 Hz. The method to increase the PCB stability in narrow space is found.

unmanned aerial vehicle; PCB; finite element model; modal analysis; anti-vibration; optimal design

10.14106/j.cnki.1001-2028.2016.12.017

TN306

A

1001-2028（2016）12-0075-06

2016-09-19

周嘉诚

湖北省教育厅科学研究计划青年人才项目资助（No. Q20141608)；国家自然科学基金青年项目资助（No. 11102141）

刘芳（1976-），女，湖北荆州人，副教授，博士后，研究方向为振动冲击分析与控制，E-mail: liufang408@163.com ；周嘉诚（1992-），男，湖北武汉人，研究生，方向为电路板可靠性研究，E-mail: 444049341@qq.com 。

时间：2016-11-29 11:41:42

http://www.cnki.net/kcms/detail/51.1241.TN.20161129.1141.017.html