三角模糊数优化的贝叶斯水质模型评价方法研究*
——以太湖竺山湾缓冲带湿地水质评价为例
吕美婷 叶 春 李春华 王亚空 干 磊
(中国环境科学研究院湖泊工程技术中心,环境基准与风险评估国家重点实验室,北京 100012)
水质评价是水资源保护的重要基础性工作。目前,有关水质评价方法的研究很多,常见的有:单因子污染指数法[1];综合污染指数法,如综合水质标识指数法、霍顿水质指数法[2]、布朗水质指数法[3]、内梅罗水污染指数法[4]等;模糊数学评价法,如模糊综合指数法[5]、模糊层次分析法[6-7]、模糊综合评价分级保证率法[8]等;灰色系统评价法[9],如灰色聚类法[10]、区域灰色决策法等;人工神经网络评价法,如反向传播算法(BP)网络模型法[11-12]、Hopfield网络模型法[13-14]、径向基函数神经网络(RBFNNs)模型法[15]等。由于水文条件、气候因素等客观原因,以及监测资料不足、精度不够、研究人员认识限制等主观原因,给水质评价工作带来了困难。目前,有关水质评价不确定性的研究主要运用模糊数学、概率统计、灰色系统和未确知数学等方法[16-18]。贝叶斯水质模型是解决水质评价过程中不确定性问题的新思路[19-21]。它是以概率统计为基础,但又与传统统计学理论不同。贝叶斯水质模型将所有参数作为随机变量,先于观测信息确定先验分布[22-24]。模糊数学是利用隶属度思想,将定性描述转化为定量描述,更好地解决不确定性强、难以量化的问题。三角模糊数是适用于数据资料较少或不够精确的情况的模糊数学法[25-26],被广泛应用于水环境健康、河流水质污染、水环境风险等评价研究中[27]。本研究将三角模糊数引入到传统的贝叶斯水质模型中,建立三角模糊数优化的贝叶斯水质模型,并将此方法应用于太湖竺山湾缓冲带湿地。具体以实际监测数据均值及标准差为基础建立三角模糊数α截集,代入优化的贝叶斯水质模型;通过计算隶属度,确定水质级别;并将水质评价结果与综合水质标识指数法以及模糊标识指数法评价结果进行比较,为太湖竺山湾缓冲带湿地水环境管理和生态建设决策提供理论基础。
1 评价方法
1.1 三角模糊数原理及运算法则

(1)
式中:μA为模糊变量的隶属度;x为某一变量。
为方便计算,通常采用α截集对三角模糊数进行处理。α为可信度,且α∈[0,1],不同可信度水平对应不同数据区间,一般取α为0.9[29]。α截集处理的计算方法如下:
(2)
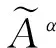
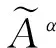
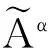
(3)
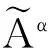
(4)
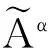
(5)
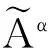
(6)
1.2 贝叶斯水质模型
1.2.1 传统贝叶斯水质模型
传统贝叶斯水质模型[30]见式(7):
(7)
式中:P(Bi,j|Aj)为第j水质指标的实测值为Aj时,水质属于i类水的概率;Bi,j表示第j项水质指标i类水质的标准值;Aj表示第j项水质指标的实测值;j为水质指标;i为水质级别,包括Ⅰ~Ⅴ,共5类;P(Bi,j)为水质属于i类水的先验概率,先于观测信息而推测得出;P(Aj|Bi,j)为第j项水质指标水质级别为i时,其值恰好为Aj的条件概率。Bi,j和Aj的单位视具体情况而定。
1.2.2 三角模糊数优化的贝叶斯水质模型

(8)

根据分层的思想及几何距离的概念计算先验概率和条件概率,计算公式如下:
(9)
(10)
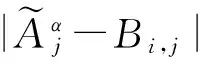
1.3 水质指标权重的确定
采用变异系数法确定各水质指标的权重[31]906,[32],计算公式如下:
(11)
(12)

1.4 水质级别及综合得分的计算
得出单项指标属于各水质级别的条件概率及其在综合水质评价中的权重,采取加权求和的方法计算水质属于各级别的综合后验概率,计算公式如下:
(13)
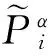
得出水质属于各级别的综合后验概率后,根据式(14)计算水质综合得分:
(14)

计算出水质综合得分后,可进一步计算水质综合得分区间[P1,P2]对水质分级标准区间[Q1,Q2]的隶属度,计算公式如下[28]1702,[33]:
(15)
式中:∣∣为区间的几何长度;∩为两个区间的交集。
水质分级标准区间见表1。

表1 水质分级标准区间
2 实例分析
2.1 研究区概况及采样点
太湖是中国第三大淡水湖泊,因地理位置及经济社会地位突出,其生态环境问题备受关注[34-35]。竺山湾位于太湖西北部,是太湖上游来水的主要汇入湖区[36]。因竺山湾具有半封闭性,以及接受河道污水汇入等原因,已成为北部湖区污染最严重,且恶化速率最快的湖区之一[37]。竺山湾缓冲带内生活污水、工业废水以及农业非点源污染是造成水质污染的主要原因之一。
2013年5月,在竺山湾缓冲带核心示范区内选取了13个典型湿地斑块进行采样,对温度、pH、溶解氧(DO)、TN、TP、氨氮、高锰酸盐指数(IMn)7个指标进行监测分析。TN采用碱性过硫酸钾消解/紫外分光光度法测定;TP采用钼锑钪分光光度法测定;氨氮采用纳氏试剂分光光度法测定;IMn按照《水质 高锰酸盐指数的测定》(GB 11892—89)测定;温度、pH和DO采用HORIBA多功能水质参数仪现场测定。采样点分布见图1,采样点基本涵盖了示范区内不同类型汇水区的湿地斑块。
2.2 太湖竺山湾缓冲带湿地水质评价
2.2.1 模型参数的选取及三角模糊化处理
根据竺山湾缓冲带湿地水质实际情况以及现有实测水质数据,选取TN、TP、氨氮、IMn和DO作为评价因子。根据三角模糊数对实测水质数据进行处理,为方便计算,采用α截集处理将三角模糊数转化为可信度水平下对应的区间数,α取0.9,经过转化的水质实测数据如表2所示。
2.2.2 先验概率及后验概率的确定
根据《地表水环境质量标准》(GB 3838—2002)中TN、TP、氨氮、IMn、DO 5项水质指标的各级水质标准以及式(9)计算先验概率,结果如表3所示。
根据式(10)计算出条件概率,并将结果代入式(8),即可计算出5个单项水质指标对各水质级别的后验概率,结果见表4。从表4可以分析出各个湿地斑块的重污染因子。例如:采样点1#的TN对Ⅳ类水的后验概率最大,而氨氮、TP、IMn和DO依次对Ⅲ、Ⅱ、Ⅲ、Ⅰ类水的后验概率最大,因此TN为采样点1#的重污染因子。采样点4#、6#、7#、12#、13#同时存在TN和COD严重污染(COD污染由IMn表征)。采样点1#、5#和9#仅存在TN严重污染,采样点2#、3#和10#的COD污染严重,采样点8#和11#同时存在TN、氨氮、TP、COD污染。
根据水质分级标准矩阵和变异系数法,计算得出TN、TP、氨氮、IMn、DO 5项指标的权重分别为0.198 6、0.204 6、0.264 8、0.198 0、0.134 0。将单项水质指标对各水质级别的后验概率及其对应的权重
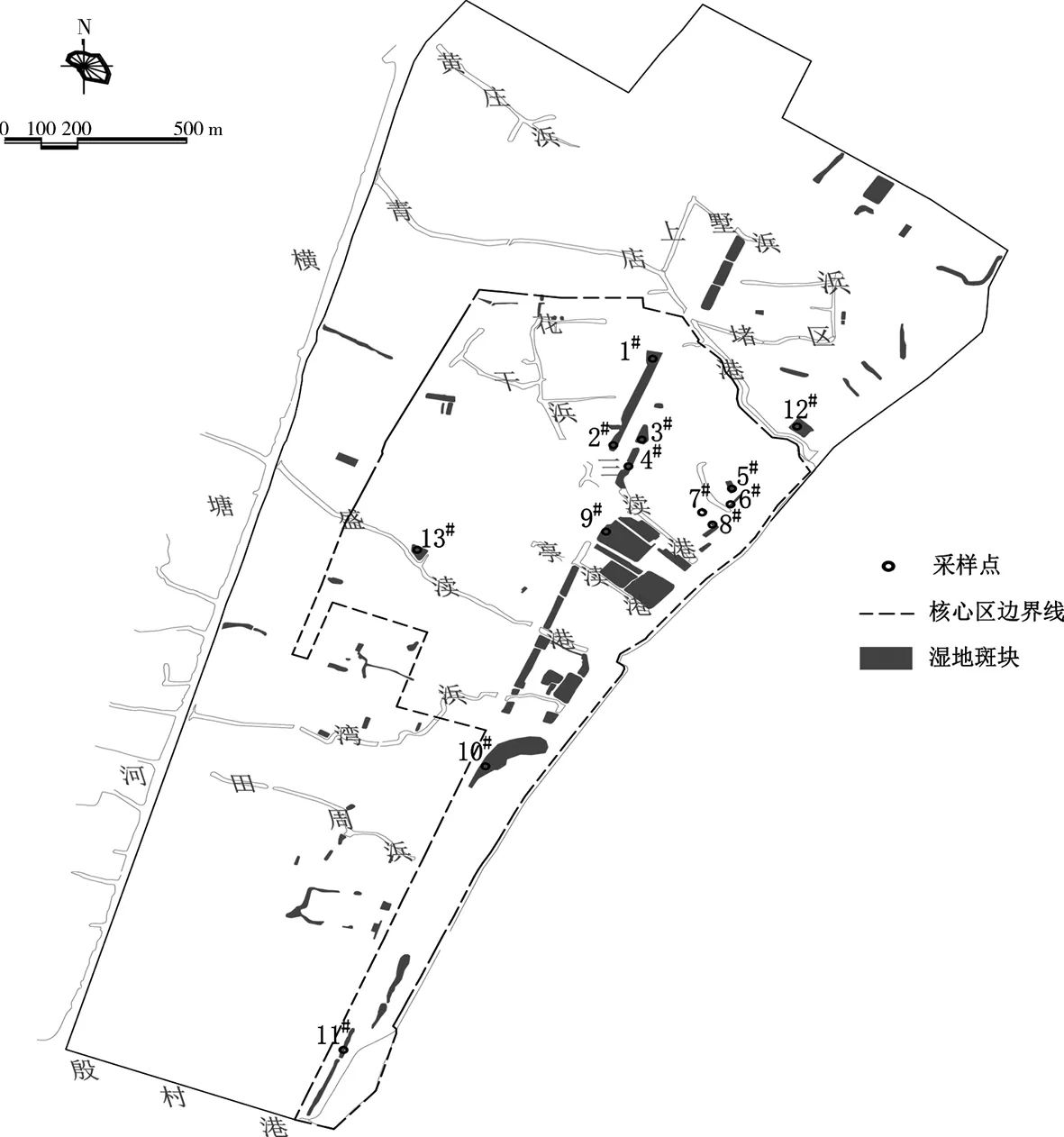
图1 太湖竺山湾缓冲带湿地采样点分布Fig.1 Sampling site distribution in Zhushan Bay buffer zone wetland of Taihu Lake
Table 2 Water quality monitoring data of Zhushan Bay buffer zone wetland treated withα-cut set technology

mg/L

表3 单项水质指标属于各水质级别的先验概率

表4 单项水质指标属于各水质级别的后验概率

表4 单项水质指标属于各水质级别的后验概率(续)

表5 各采样点水质属于各水质级别的综合后验概率
代入式(13),即可得出各采样点水质对各水质级别的综合后验概率,结果见表5。从表5可以看出,各采样点的水质级别并不具有唯一性,只是相对来说,对某一级别的综合后验概率最大,如采样点1#,水质级别为Ⅲ类的可能性最大。
2.2.3 不同水质评价方法的评价结果比较
采用余勋等[31]906对各级别水质的综合打分方法,对Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ类水依次赋值5、4、3、2、1,然后根据式(14),计算各采样点水质综合得分,得出水质综合得分区间,并根据式(15)计算水质综合得分区间对水质分级标准区间的隶属度,确定水质级别。同时,采用综合水质标识指数法[38]和模糊标识指数法[39]对研究区内13个采样点的水质情况进行了评价,并对不同水质评价方法产生的结果进行了比较(见表6)。
从表6可以看出,3种评价方法对同一水质的评价结果存在差异,仅少数采样点的水质评价结果一致,表明水质评价工作中,评价模型对评价结果有一定的不确定性。总的来说,三角模糊数优化的贝叶斯水质模型法对竺山湾缓冲带湿地水质的评价结果与综合水质标识指数法、模糊标识指数法得出的评价结果相似度均为46%左右;而综合水质标识指数法和模糊标识指数法的评价结果相似度较低。
综合水质标识指数法和模糊标识指数法的共同优点在于,百分位表示参与评价的水质指标中劣于目标水质的指标数,千分位表示综合水质级别劣于目标水质的等级;而且,两者都可以对劣Ⅴ类水进行评价。然而,也分别存在以下缺点:综合水质标识指数法忽略了水质评价过程中的各种不确定性因素,如测量结果及分析过程的不确定性、模型结构的不确定性等等,而将各项评价指标进行平均,未考虑各指标对水质级别的贡献存在一定差异,因而在水质评价定级上有一定误差;模糊标识指数法在传统模糊层次分析法的基础上有所改进,改善了传统方法低估水体污染程度方面的不足。三角模糊数优化的贝叶斯水质模型在水质评价过程中综合考虑了指标监测数据的不确定性以及模型结构的不确定性。首先,根据几何距离概念对先验概率进行分层确定;其次,在确定单项指标后验概率过程中,将实测值的平均值和标准差进行三角模糊化处理后引入评价模型,考虑了参评指标在一定置信度水平下的波动范围,大大提高了水质评价结果的真实性。
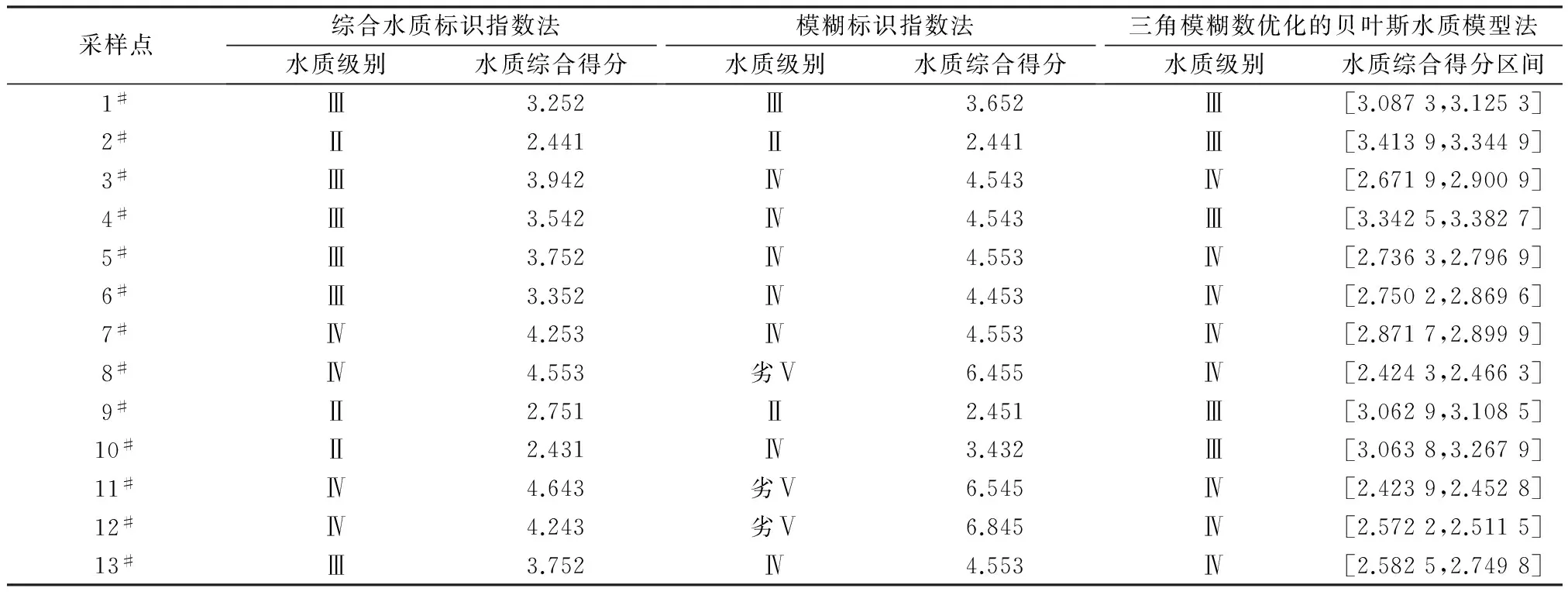
表6 基于不同水质评价方法的竺山湾缓冲带湿地水质评价结果1)
注:1)综合水质标识指数法和模糊标识指数法的水质综合得分越高,则水质越差;相反,三角模糊数优化的贝叶斯水质模型法的水质综合得分越高,则水质越好。
三角模糊数优化的贝叶斯水质模型对太湖竺山湾湿地水质的评价结果显示:13个采样点水质级别评价结果为Ⅲ~Ⅳ类水,而根据《太湖流域水环境综合治理总体方案》和《江苏省太湖流域水环境综合治理实施方案》对水功能区级别的划分,竺山湾隶属一级功能区,目标水质级别为Ⅰ类。因此,竺山湾缓冲带湿地内的13个湿地斑块的水质均未达到目标水质标准。
3 讨论与结论
3.1 讨 论
三角模糊数考虑了实测值的随机误差、采样点具体位置引起的监测结果差异等不确定性因素,尤其适合处理资料较少、精度不够等情况下的水质信息。因此,将三角模糊数引入太湖竺山湾缓冲带湿地的水质评价过程,使评价结果更为客观合理。
贝叶斯水质模型利用已知信息,统计推断出多种可能性,并以最大可能性做出最终判断,是一种针对小样本的、可行的水质评价方法。在水质评价中则体现为根据水质综合得分区间对水质分级标准区间的隶属度,判定水质级别。传统贝叶斯水质模型中,先验概率均匀分布。本研究根据GB 3838—2002各指标水质分级标准,引入几何距离的概念,分层计算先验概率;同时以各因子加权求和的方法计算得出综合后验概率,全面考虑了各参评水质指标对水质评价定级的贡献率,使得评价结果更加真实可靠。
三角模糊数优化的贝叶斯水质模型法综合了三角模糊数和传统贝叶斯水质模型的优点,同时考虑了水质评价模型结构和参数的不确定性。得出的水质综合得分及水质级别均是基于模糊数学思想的,带有隶属度信息的,能更好地反映竺山湾缓冲带湿地水质真实情况。
3.2 结 论
竺山湾缓冲带湿地内水体水质都为Ⅲ~Ⅳ类,未能符合Ⅰ类目标水质要求。从总体上看,竺山湾缓冲带湿地水体的TN和COD污染较严重,TP、氨氮和DO并非重污染因子。因此,在后期的生态修复及水质改善研究工作中应主要针对削减氮和有机物污染开展。
[1] 徐祖信.我国河流单因子水质标识指数评价方法研究[J].同济大学学报(自然科学版),2005,33(3):321-325.
[2] RAMOSJ A. Applications of TLS and related methods in the environmental sciences[J].Computational Statistics & Data Analysis,2007,52(2):1234-1267.
[3] 周敏.饮用水水质指数分析及其在基层的应用研究[D].上海:复旦大学,2011.
[4] 黄海东,张克峰.小城镇水源水质评价方法选择方案探讨[J].水利科技与经济,2010,16(7):736-738,740.
[5] 杨静.改进的模糊综合评价法在水质评价中的应用[D].重庆:重庆大学,2014.
[6] 徐兵兵,张妙仙,王肖肖.改进的模糊层次分析法在南苕溪临安段水质评价中的应用[J].环境科学学报,2011,31(9):2066-2072.
[7] 卢文喜,李迪,张蕾,等.基于层次分析法的模糊综合评价在水质评价中的应用[J].节水灌溉,2011(3):43-46.
[8] 张美华,陈宏.几种模糊聚类法在环境质量综合评价中的应用[J].重庆环境科学,1999,21(3):13-16.
[9] 陆洲,夏秋颖,周琳,等.等斜率灰色聚类法在地面水环境质量评价中的应用[J].环境保护科学,2000,26(5):43-46.
[10] 贺北方,王效宇,贺晓菊,等.基于灰色聚类决策的水质评价方法[J].郑州大学学报(工学版),2002,23(1):10-13.
[11] 李文娟.改进BP神经网络在水质评价中的应用研究[D].重庆:重庆理工大学,2011.
[12] 黄胜伟,董曼玲.自适应变步长BP神经网络在水质评价中的应用[J].水利学报,2002,33(10):119-123.
[13] 初海波,卢文喜,尹津航,等.BP网络、Hopfield网络在水质评价应用中的比较研究[J].中国农村水利水电,2011(10):70-72.
[14] 卢文喜,初海波,王喜华,等.基于因子分析的Hopfield神经网络在水质评价的应用[J].水土保持通报,2012,32(1):197-200.
[15] 周丰,郭怀成,刘永,等.基于多元统计分析和RBFNNs的水质评价方法[J].环境科学学报,2007,27(5):846-853.
[16] GRONEWOLD A D,STOW C A,VIJAYAVEL K A,et al.Differentiatingenterococcusconcentration spatial,temporal,and analytical variability in recreational waters[J].Water Research,2013,47(7):2141-2152.
[17] GRONEWOLD A D,BORSUK M E.Improving water quality assessments through a hierarchical Bayesian analysis of variability[J].Environmental Science & Technology,2010,44(20):7858-7864.
[18] 尹海龙,徐祖信.河流综合水质评价方法比较研究[J].长江流域资源与环境,2008,17(5):729-733.
[19] WELLEN C,ARHONDITSIS G B,LONG Tanya,et al.Quantifying the uncertainty of nonpoint source attribution in distributed water quality models:a Bayesian assessment of SWAT’s sediment export predictions[J].Journal of Hydrology,2014,519:3353-3368.
[20] HADDAD K,EGODAWATTA P,RAHMAN A A.Uncertainty analysis of pollutant build-up modelling based on a Bayesian weighted least squares approach[J].Science of the Total Environment,2013,449:410-417.
[21] 孙鹏程,陈吉宁.基于贝叶斯网络的河流突发性水质污染事故风险评估[J].环境科学,2009,30(1):47-51.
[22] 黄凯,张晓玲.贝叶斯方法在水环境系统不确定性分析中的应用述评[J].水电能源科学,2012,30(9):47-49.
[23] 廖杰,汪嘉杨,丁晶.基于改进贝叶斯模型的四川省主要河流水质评价[J].四川师范大学学报(自然科学版),2009,32(4):518-521.
[24] 郁章文.基于贝叶斯方法的三峡库区水环境质量研究[D].济南:山东大学,2008.
[25] SANGAIAHA A K,THANGAVELU A K.An exploration of FMCDM approach for evaluating the outcome/success of GSD projects[J].Central European Journal of Engineering,2013,3(3):419-435.
[26] HUANG Guangqiu,PAN Changbo.Introduction of probabilistic risk assessment approach to analyze the safety of MVS[J].Procedia Engineering,2011,26:2027-2031.
[27] 赵锋霞.基于不确定性参数的水环境健康风险评价方法及应用[D].大连:辽宁师范大学,2013.
[28] 樊梦佳,袁兴中,祝慧娜,等.基于三角模糊数的河流沉积物中重金属污染评价模型[J].环境科学学报,2010,30(8).
[29] 李如忠,洪天求,金菊良.河流水质模糊风险评价模型研究[J].武汉理工大学学报,2007,29(2):43-46.
[30] YANG Likun,ZHAO Xinhua,PENG Sen,et al.Integration of Bayesian analysis for eutrophication prediction and assessment in a landscape lake[J].Environmental Monitoring and Assessment,2014,187(1):1-19.
[31] 余勋,梁婕,曾光明,等.基于三角模糊数的贝叶斯水质评价模型[J].环境科学学报,2013,33(3).
[32] 屈卫军.基于变异系数法的灰色关联决策模型在节水工程方案优选中的应用[J].地下水,2010,32(5):50-51.
[33] 祝慧娜,袁兴中,曾光明,等.基于区间数的河流水环境健康风险模糊综合评价模型[J].环境科学学报,2009,29(7):1527-1533.
[34] 许嫚,刘晓收,刘清河,等.太湖竺山湾湖泊缓冲带内湿地浮游植物季节变化[J].海洋湖沼通报,2014(4):41-51.
[35] 吕美婷,赵德华,杨棠武,等.湖泊重要入湖河流稳定水像元提取技术[J].环境监控与预警,2013,5(5):6-9.
[36] 张明礼,杨浩,林振山,等.太湖竺山湾底泥中有害物质含量与环境污染评价[J].中国环境科学,2011,31(5):852-857.
[37] 王雯雯,姜霞,王书航,等.太湖竺山湾污染底泥环保疏浚深度的推算[J].中国环境科学,2011,31(6):1013-1018.
[38] 徐祖信.我国河流综合水质标识指数评价方法研究[J].同济大学学报(自然科学版),2005,33(4):482-488.
[39] 王肖肖,张妙仙,徐兵兵.模糊标识指数与对应分析法在水质评价中的联合应用[J].环境科学学报,2012,32(5):1227-1235.

