考虑多作业路径的集装箱甩挂运输调度优化

罗志勇

(北京铁路局丰台货运中心,北京116026)

1 引言

甩挂运输利用并行工作的原理大大缩短了牵引车等待货物装卸及其在物流中心排队的时间,提高了牵引车的作业效率。

国外关于甩挂作业调度的研究起步较早。Caris et al提出了基于插入法的两阶段启发式算法,对具有时间窗约束的集装箱甩挂运输作业调度问题进行求解。Lin et al应用模拟退火算法来求解甩挂作业调度问题,所获得的基准问题求解结果优于运用禁忌搜索的求解结果。Lin et al构建了放松车辆数量约束的甩挂作业调度数学模型,以从更大的邻域内搜索是否存在可进一步减少运送距离的可行解,并设计了模拟退火算法对其进行求解。Derigs et al对于具有时间窗约束的甩挂作业调度问题,提出了由局部搜索、大规模邻域搜索和标准的泛启发式控制策略相结合的混合算法进行求解。相比国外众多研究成果,国内关于甩挂运输调度优化方面的研究则刚刚起步,研究成果较少。胡志华等建立了在集装箱集散环境下空重箱循环甩挂的调度优化模型,并设计两阶段优化算法进行求解。胡志华等为甩挂运输带有子回路的新型路径优化问题建立了0/1整数规划模型,采用混合进化算法进行求解。

基于以上研究成果,本文在轴辐式网络中的一点多线甩挂运输组织模式下,对任务的作业路径进行分类转换后建立了考虑多作业路径的集装箱甩挂运输牵引车调度优化模型,并设计了启发式算法的模拟退火算法求解。算例分析验证了模型与算法的有效性与实用性。

2 问题描述

2.1 运输网络描述

每个甩挂运输网络由若干个轴辐式子网络构成,每个轴辐式子网络的中心为甩挂运输中心,客户点分布在甩挂中心周围。设轴辐式子网络结构图G＝(V,A),其中,V＝{0,1,…,n},顶点0表示甩挂中心,顶点1,…,n表示客户节点,A表示顶点0,1,…,n之间距离弧的集合。图1表示的是一个轴辐式子网络图。

在图1中,0表示甩挂中心,1到n表示客户节点。牵引车每天从甩挂中心出发去执行取箱任务或送箱任务,待所有任务执行完之后返回甩挂中心。

2.2 任务路径描述

图1 轴辐式子网络图

取箱任务是指若某客户点处有装卸完毕的挂车,牵引车到达该客户点后立即挂上重箱后送回甩挂中心。送箱任务是指某客户点处有货物等待装箱,牵引车拖带一个空箱到达指定客户点后甩下空箱即可去完成其它任务,待该点集装箱装卸完毕后成为一个新的取箱任务。在执行每个任务时,牵引车的来源是不确定的,若上一个任务为取箱任务则牵引车的来源为甩挂中心;若上一个任务为送箱任务,则牵引车的来源为上一个任务的客户点。在途牵引车经过的路径根据前后任务节点可以归为以下四类:(1)上一任务是取箱任务,下一任务是取箱任务;(2)上一任务是取箱任务,下一任务是送箱任务;(3)上一任务是送箱任务,下一任务是取箱任务;(4)上一任务是送箱任务,下一任务是送箱任务。这四类路径可由图2表示。

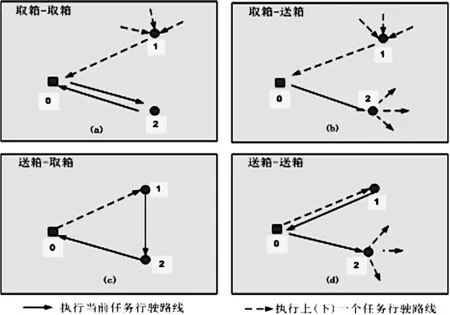
图2 四种车辆路径类型

图2中顶点0代表甩挂中心,顶点1、2表示客户需求点。实线箭头表示执行当前任务行驶路线,虚线箭头表示执行上(下)一个任务行驶路线。为便于求解,本文将每个任务的出发点和终到点结合成一点,则图2的四种车辆路径类型转变为图3。

图3 四种车辆路径类型转换图

在图3中,1-0表示从客户点1到甩挂中心的取箱任务,0-0表示牵引车从甩挂中心到甩挂中心的虚拟行驶路径。从图3中的四种车辆路径类型可以看出,牵引车行驶路线如图4所示。与传统多重旅行商问题不同的是,任务节点是由出发点和终到点结合后形成的一点,且该牵引车行驶路线可能存在虚拟路径。

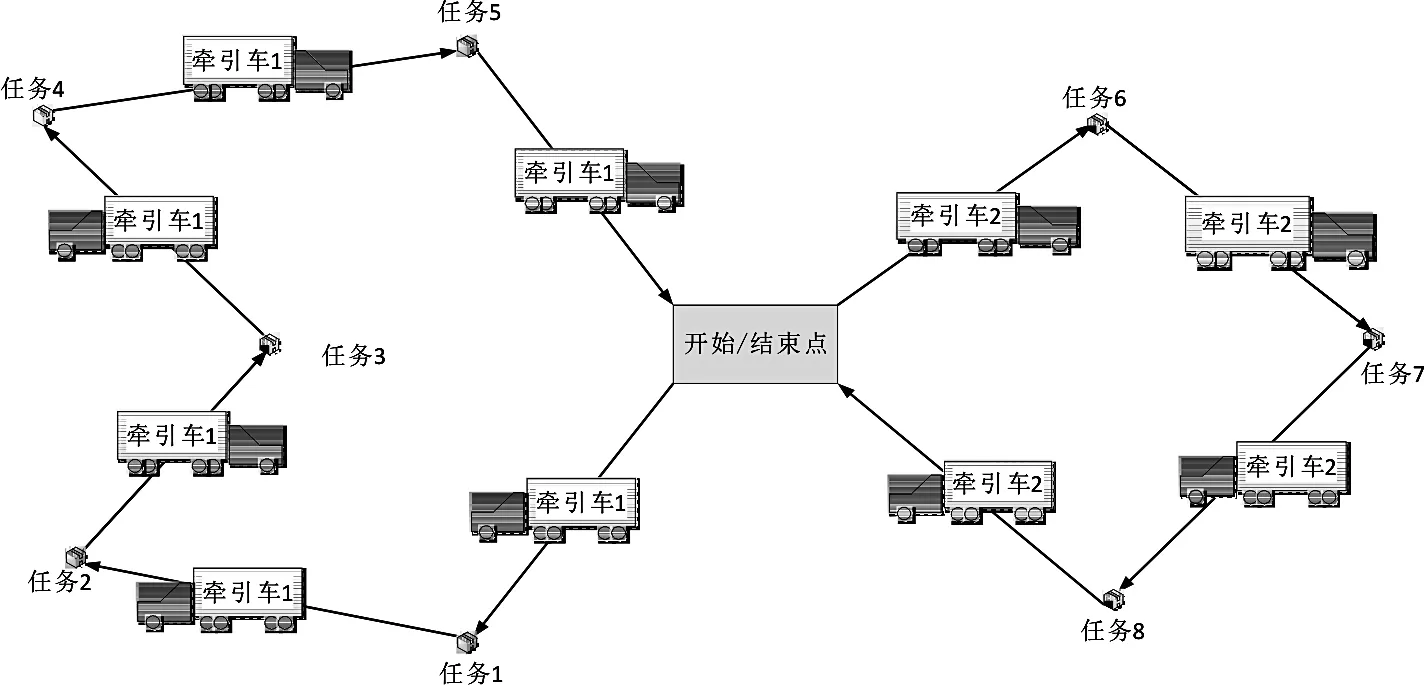
图4 牵引车行驶路线

3 混合整数规划模型建立

3.1 假设条件

根据甩挂中心实际操作情况及解决实际问题的需要,做出如下假设:

(1)所有的任务在调度之前都已确定,中途不会增加其它任务;(2)所有牵引车和挂车都采用统一标准尺寸;(3)一辆牵引车一次只拖挂一辆挂车;(4)牵引车拖挂重箱和拖挂空箱的速度相同;(5)牵引车拖上挂车以及取下挂车的时间不计;(6)牵引车每天从甩挂中心出发,最后返回到甩挂中心。

3.2 参数说明

M:任务的数量;K:牵引车的数量;tij:从任务i到任务j的时间;fi:执行任务i所需的时间;wi:在执行任务i时的等待时间;ti:到达任务i的对应客户点的时间;Rk:牵引车k的一天工作时间;[ETi,LTi]:表示任务i要求开始的时间窗。

3.3 模型建立

目标函数:

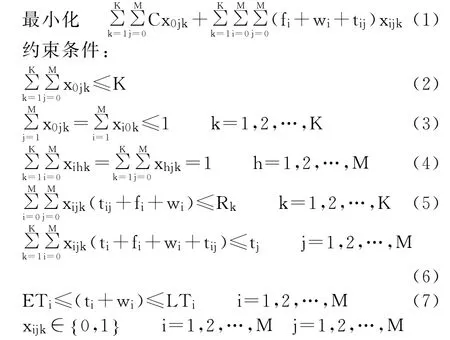
式(1)为目标函数,表示使牵引车的数量最少和总的行驶时间最短,C为一个足够大的常数,故保证了减少牵引车数量的优先级高于总的行驶时间最短;式(2)表示从甩挂中心出发的牵引车数量不大于车辆总数;式(3)表示每辆牵引车每天从甩挂中心出发,执行完一天任务后回到甩挂中心;式(4)表示每个任务仅且只被执行一次;式(5)表示每辆牵引车的行驶时间不能超过其一天的工作时间;式(6)表示任务的被完成的先后顺序约束;式(7)表示任务的开始执行时间必须在时间窗的范围之内;式(8)表示决策变量。

3.4 惩罚成本函数

本文的时间窗采用软时间窗。牵引车开始执行任务i的时间若在ti1之前或ti2之后,将付出较高的惩罚成本固定值M;若在[ti3,ti4]范围内,惩罚成本为0;若在[ti1,ti3]范围内,单位时间的惩罚成本为a;在[ti4,ti2]时间范围内到达,单位时间的惩罚成本为b。图5为第k辆牵引车执行第i个任务所付出的惩罚成本函数图像。式(9)为相应的惩罚成本函数。

图5 惩罚成本函数图

4 基于启发式规则的模拟退火算法求解

本文采用二维解矩阵的编码方式进行解的表示。在解的变换过程中,反复交换二维解矩阵中两个不等于0的值以得到新解,这种解的反复变换过程类似于模拟退火算法的加温过程。图6为基于启发式规则的模拟退火算法流程图。

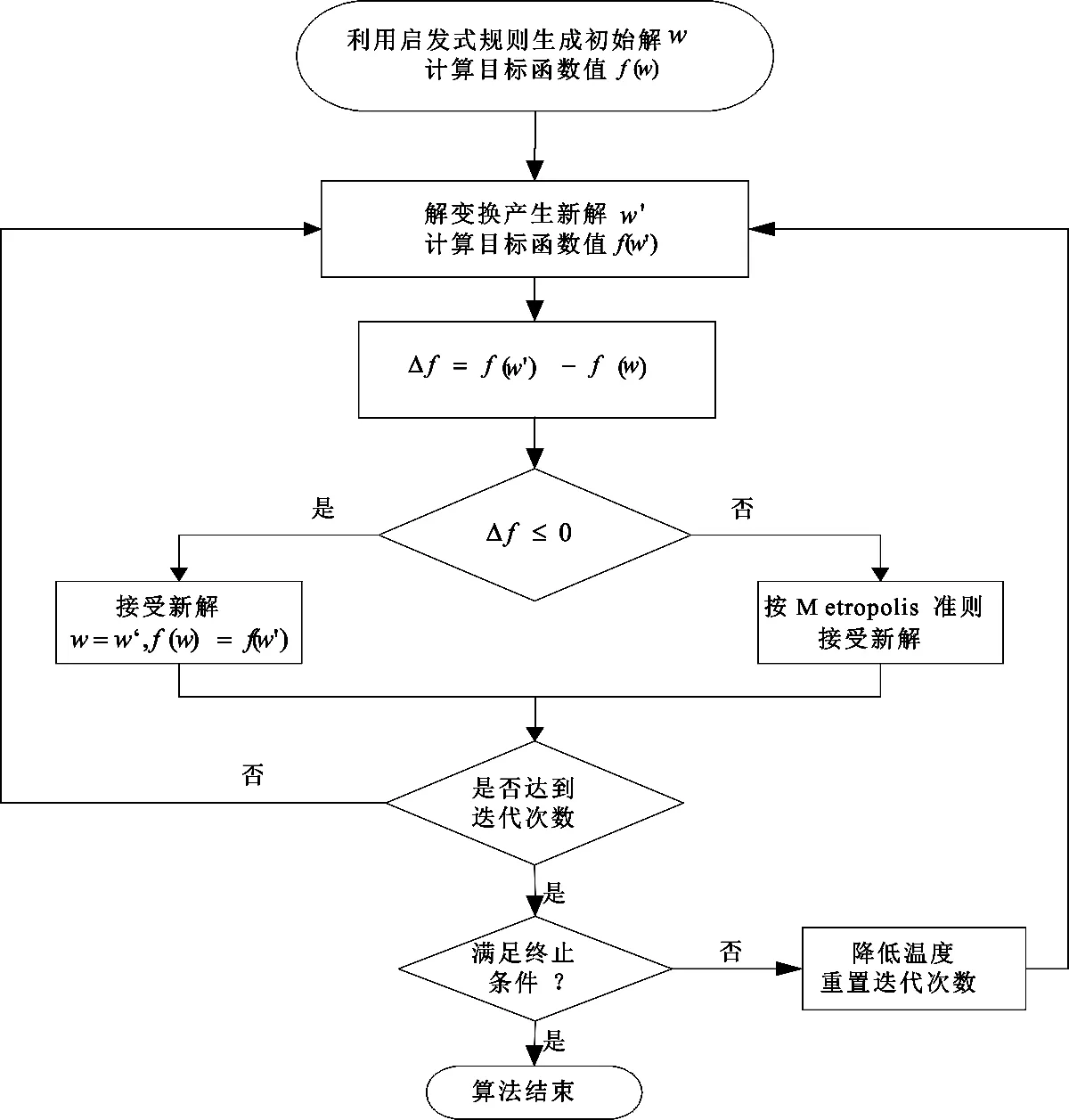
图6 基于启发式规则的模拟退火算法流程图

4.1 启发式规则生成初始解

将n个任务按照可接受时间窗上限从早到晚进行排序,形成任务集合M＝{1,2,…,n},将所有牵引车形成集合K＝{1,2,…,m}。设计启发式规则生成初始解流程图如图7,具体实现步骤如下:

Step 1:设未完成任务集L＝M,任务i＝1(i∈M),牵引车j＝1(j∈K),进入step 2;

Step 2:将任务集L按照时间窗顺序进行从小到大排序,进入step 3;

Step 3:依次判断任务i是否能加入到第j辆牵引车的任务集中,判断依据为,是否满足时间窗要求。若满足,则L＝L/i,进入step 4;否则,令j＝j＋1,重复执行step 3;

Step 4:判断L是否为空集,若是,则输出初始解;否则令i＝i＋1,转到Step 3。

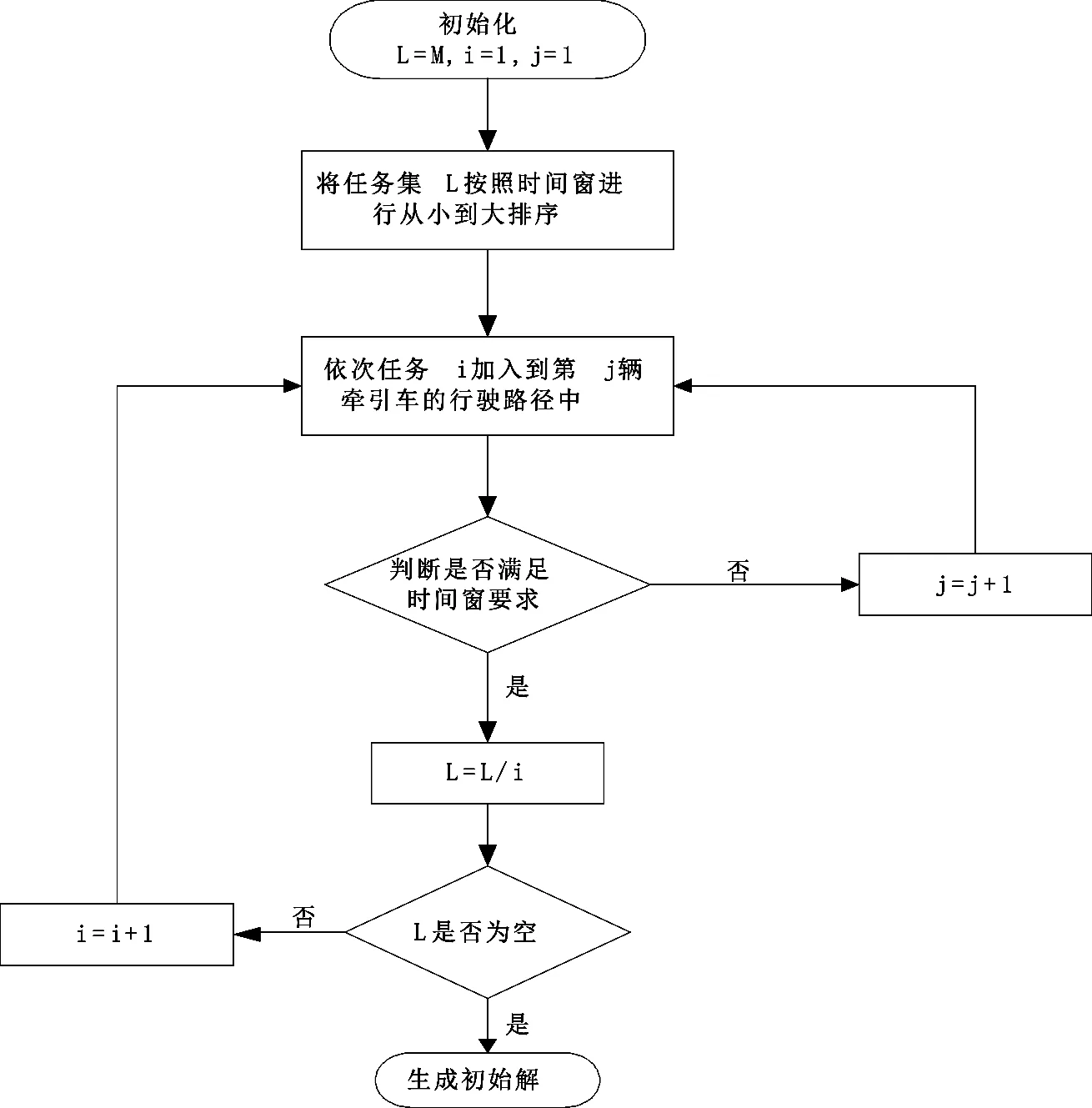
图7 启发式算法流程图

4.2 解的编码方式

二维解矩阵中的值为任务编号,每一行表示一辆牵引车的行驶路径。图8表示一个需使用4辆牵引车,完成20个任务的甩挂运输方案,其中这四辆牵引车的行驶路径分别为5-6-8-16-15;7-9-14-17-18;2-4-10-13-20;1-3-11-12-19。

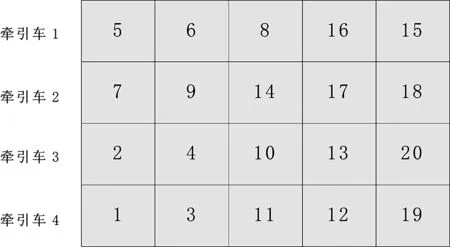
图8 解的编码方式

但是,按照上述编码方式,运输方案中的牵引车数量和每辆牵引车所完成的任务数是固定的,不利于保证解变换时搜索到全部可行解。为了扩大解的搜索空间,对解矩阵进行放大,每行每列增加足够的0位。0并无实际意义,仅起到扩大解的规模的作用。图8的解矩阵扩大规模后见图9,此时该运输方案的牵引车数量由原来的4辆变为[3,6]范围内的任一整数值,每辆牵引车完成的任务数也由原来的5个变为[2,7]范围内的任一整数值,极大扩大了可行解规模。

4.3 解变换

采用产生随机数方法交换矩阵中的两个数,若生成的两个数对应在解矩阵中的值都是0,则重新产生两个数,直到不都为0为止,生成新解。在图10中,解的规模是42,在[1,42]范围内随机产生两个整数,确定两个位置,在当前解中将这两个位置的数值进行对换。假设产生的两个数是9和18,则在解矩阵中,把第9个元素和第18个元素对调,其对应数值分别为9和13,对调9和13的位置产生新的解矩阵。

图9 扩大规模后的解

图10 新解生成方法

5 算例分析

以某公司甩挂中心的运营数据为基础,对其每日的运输方案进行优化。为了保证算例分析的可重复性及其与实际分布规律的拟合程度,本文使用matlab中的unidrnd函数随机生成客户点的坐标,用unidrnd函数生成的随机数呈离散均匀分布。二维均匀分布的函数为,x,y为自变量。设甩挂中心的坐标为表1为某次随机生成的客户点坐标,此时a＝c＝0,b＝d＝30,甩挂中心的坐标为(15,15)。

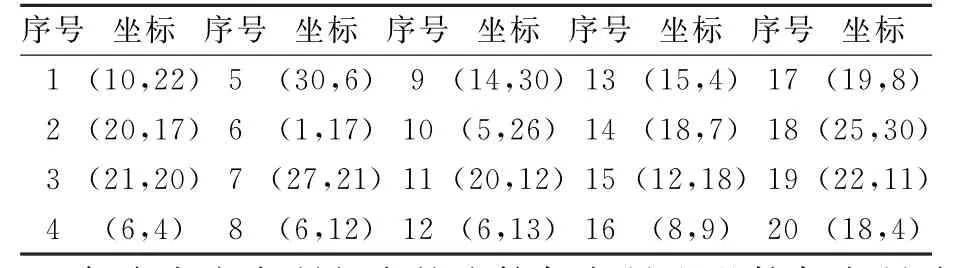
表1 客户点位置

每个客户点所包含的取箱任务量和送箱任务量为[0,a]内的任意随机整数,可用matlab中的randpint函数实现。表2为表1中所有客户随机生成的任务数量。本文取a＝2。

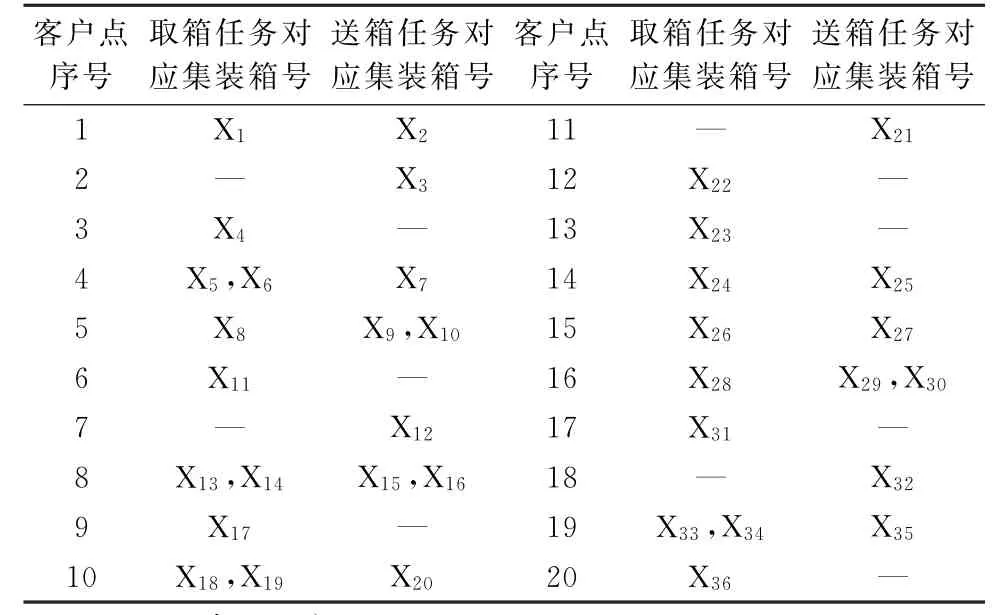
表2 客户点任务量

根据客户时间窗的特性,使用unifrnd函数随机生成每个任务的要求开始时间,然后使用round函数保证生成的随机数为整数。在每个任务的可接受时间窗等于要求的时间窗减去或加上一个固定的时间t0(t0≠0)。本文取t0＝30。表3为对表2中所有任务随机生成的时间窗。

牵引车每天从甩挂中心开始发车的时刻为6:00,平均以40km/h的速度行驶,甩挂中心与客户点之间和客户与客户之间的欧氏距离等于坐标距离的两倍,牵引车早于任务的时间窗上限和晚于时间窗下限的惩罚系数为50。

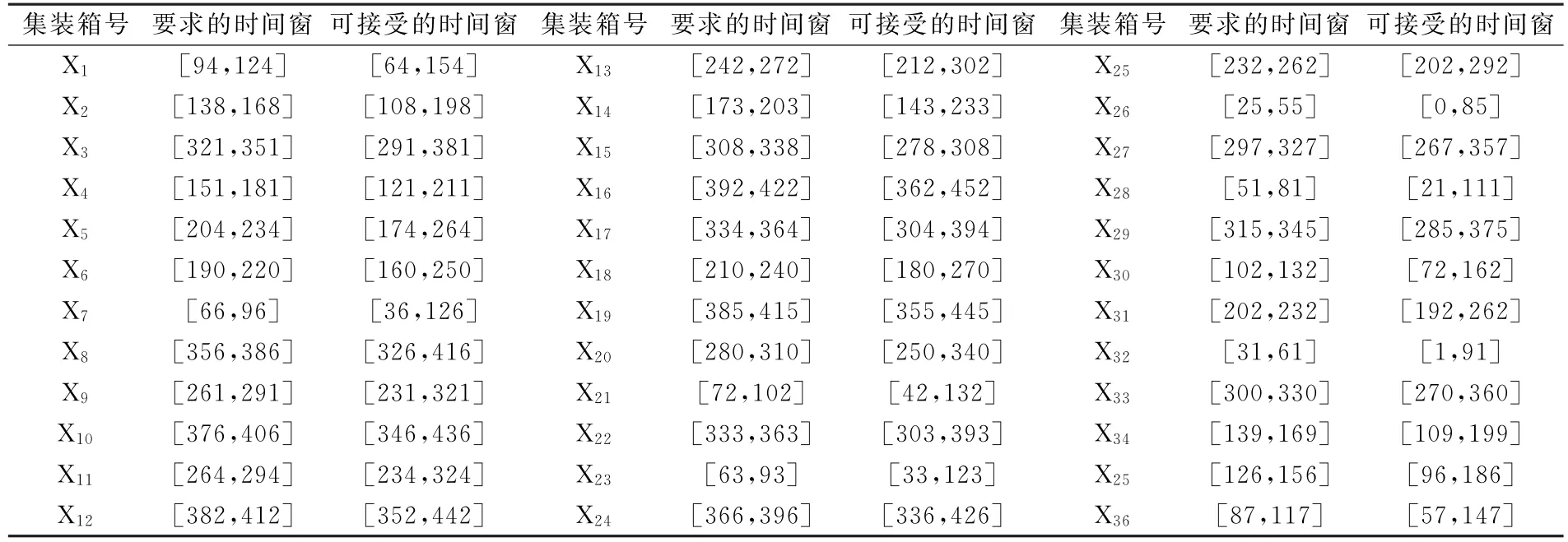
表3 各任务对应的时间窗

根据上述数据,设计结合启发式规则的模拟退火算法,对模型进行求解。初始温度T0＝1000,内循环次数L＝500－T/4(T为当前温度),终止温度Tend＝1,降温速率α＝0.8。求得最优解为:需要4辆牵引车,执行任务所需时间为6968,目标函数的收敛情况如图11。从图11可以看出,算法在9000次左右收敛到极值点6986。收敛速度很快,而且算法比较稳定。

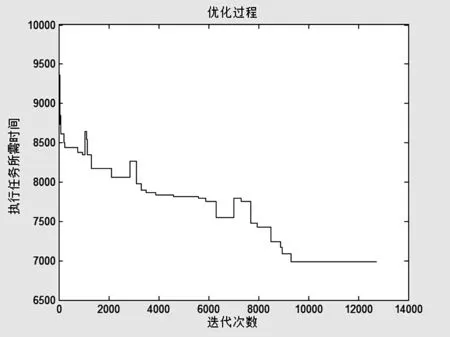
图11 模拟退火算法收敛图

牵引车的最优行驶路线如表4。

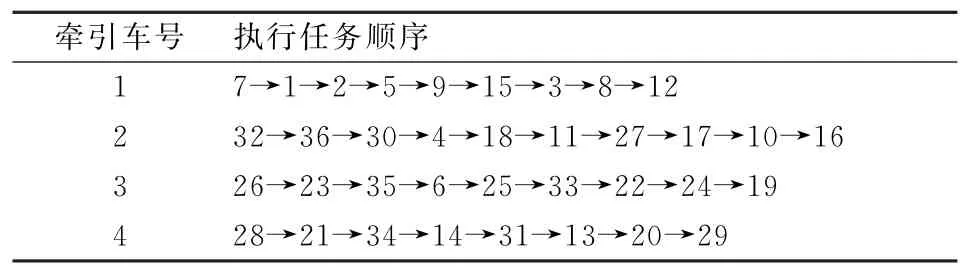
表4 牵引车执行任务顺序

数据结果表明,提出的模型和算法能够为牵引车的调度提供最优方案。

另外,在甩挂运输的实际调度规则用最多的是基于时间紧迫度的启发式规则,即空的牵引车每次都去执行时间上最紧迫的任务。使用matlab编程可得,实际调度规则得到的执行任务所需时间为8642,牵引车的执行任务顺序如表5。

与实际调度规则进行比较可知,本文的模型和算法从完成所有任务的时间最少上进行考虑,得到的执行任务时间比实际调度规则的执行任务时间减少了19.37%。算例结果表明,本文的模型和求解算法对甩挂作业调度人员具有一定的实际指导意义。

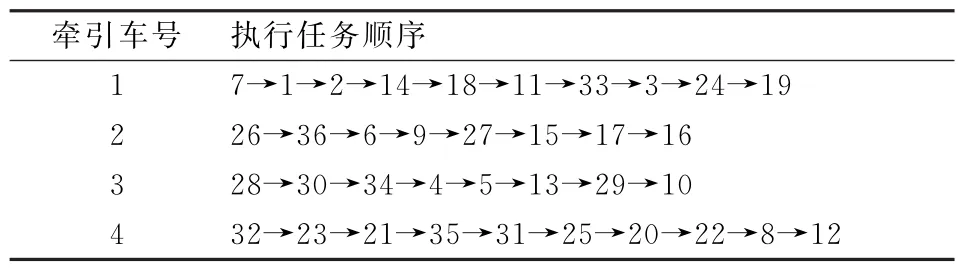
表5 实际调度规则执行任务顺序

6 结论

本文在轴辐式网络中的一点多线甩挂运输组织模式下,考虑了多作业路径并进行分类转换后建立集装箱甩挂运输牵引车调度优化模型,并设计了基于启发式规则的模拟退火算法对模型进行求解,借助matlab编程得以实现。通过算例分析与实际调度规则进行比较,运算结果证明了模型和算法的有效性和实用性。进一步的研究将集中于甩挂运输任务集动态调度优化,即调度过程中可能增加其它任务。

[1]Caris A.,Janssens G.K.A local search heuristic for the pre-and end-haulage of intermodal container terminals[J].Computers&Operations Research,2009,36(10).

[2]Lin Shih Wei,Yu Vincent F,Chou Shuo Yan.Solving the truck and trailer routing problem based on a simulated annealing heuristic[J].Computers&Operations Research,2009,36(5).

[3]Lin Shih Wei,Yu Vincent F,Chou Shuo Yan.A note on the truck and trailer routing problem[J].Expert Systems with Applications,2010,37(1).

[4]Lin Shih Wei,Yu Vincent F,Lu Chung Cheng.A simulated annealing heuristic for the truck and trailer routing problem with time windows[J].Expert Systems With Applications,2011,38(12).

[5]Derigs Ulrich,Pullmann Markus,Vogel Ulrich.Truck and trailer routing-Problems,heuristics and computational experience[J].Computers&Operations Research,2013,40(2).

[6]胡志华等.集装箱集散的空重箱循环甩挂调度方法[J].武汉理工大学学报,2012,(10).

[7]胡志华.集装箱码头间互拖的集卡甩挂运输调度问题[J].重庆交通大学学报,2013,32(2).

[8]胡志华等.基于混合进化算法的甩挂配送问题[J].公路交通科技,2013,30(5).