也谈“数形结合百般好,割裂分家万事休”
蔡庆全
我国著名数学家华罗庚曾说:“数形结合百般好,割裂分家万事非。”数与形是现实世界中客观事物的抽象和反映,同时也是我们的数学的基石。“数”主要指实数、复数或代数对象及其关系,属于数学抽象思维范畴,是人的左脑思维的产物。而“形”主要指几何图形,属于形象思维范畴,是人的右脑思维的产物,数形结合使人充分运用左、右脑的思维功能,相互依存、彼此激发,全面、协调、深入发展人的思维能力。我们认为,数形结合,主要指的是数与形之间的一一对应关系。数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而达到优化解题途径的目的。数形结合思想方法能巧妙地实现数与形之间的互换,使得看似无法解决的问题简单化、明朗化,让人有“山重水复疑无路,柳暗花明又一村”的感觉。数形结合思想方法在解题中的重要性决定了它在平时的教学中也应该受到重视。在数学教学中教师要有意识地沟通数与形之间的联系,帮助学生逐步树立起数形结合的观点,提高主动应用的意识,并使这一观点扎根到学生的认知结构中,成为运用自如的思想观念和思维工具,从而提高学生的数学修养与解题能力。而在小学数学教学中,如果能突出数形结合思想,那将非常有利于学生从不同的侧面加深对问题的认识和理解,提供解决问题的方法,也有利于培养学生将实际问题转化为数学问题的能力。
案例一:
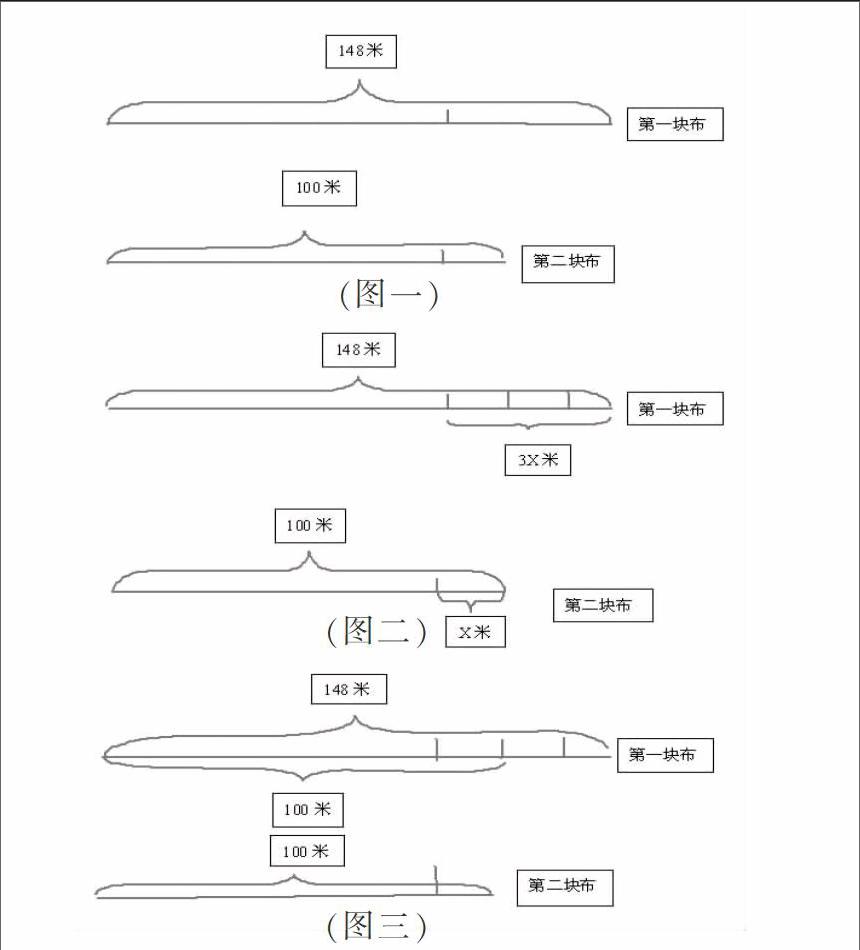
笔者在六年级一次授课过程遇到这么一道题:“有两块布料,第一块长148米,第二块长100米。两块布料各剪去同样长的一段后,第一块剩下的长度是第二块的3倍,两块布料各剩下多少米?”当时全班学生炸开了锅。生1:“这道题没法解,不告诉我们剪去多少米就不知道剩下的米数”生2反驳道:“那还叫你求,不如回到一年级去读。”生3(慢条斯理):“你两别争,用我们已学过的方程知识来解答准行。”生4:“那该设谁为x米?”很多学生随声应和。这时刻我相机说道:“同学们再认真把题目读两遍,找找看,准能找出题中相等的数量关系。”经我这么一提醒,班级顿时安静下来,学生陷入思考中。生5:“应该设第二块布剩下部分为x米,得到方程为100-x=148-3x.”生6:“我知道这个方程两边的数量关系,但我们没解过这种方程不知道怎样解。”全班大约有的学生站起来说:“对!只会列式不会解!”我笑着回答:“同学们先别急,你们想想看,列方程解决问题除了要找数量关系外,我们还可以请什么来帮忙?”生齐答:“画线段图。”此时,我顺水推舟组织全体学生根据题意画出线段图:
引导学生从图一认真观察到图三,生7:“3x-x=148-100.”就这样,一道学生不会解答的问题在我的组织下迎刃而解。
案例二:
小学数学新课标提出:“学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。”国标苏教版教材六年级上册第18页第9题:“学校科技馆大门前有5级台阶,每级台阶长6米,宽0.3米,高0.2米。(1)5级台阶一共占地多少平方米?(2)给这些台阶铺上地砖,至少需要铺多少平方米地砖?”解答第(1)个问题学生没有疑义,在解答第(2)个问题时,学生争议很大。生1:台阶两旁是否有其他建筑?生2:台阶是一旁靠建筑还是独立呈现?生3:照你俩的想法(指着前面两位学生)我认为本题有3种答案:第一台阶两旁被其他建筑物包围不用贴瓷砖;第二台阶一旁被建筑物包围,另一旁裸露的;第三台阶两旁都裸露着。我并没有打断他的发言,而是肯定了她的想法并给予及时表扬:“你真是个有心人,在我们的校园内就存在着这三种情况的台阶,第一种情况是在教学楼与行政楼之间的台阶;第二种情况是在要去行政楼二层的户外小台阶;第三种情况是在厕所前的长台阶。课后老师与你们一起去看看核实这三种情况,好吗?”课后,我带领全班学生到该三处地方一起观察,帮助学生解决课中产生的疑惑。

