4个单因素完全随机试验数据的联合方差分析

宋希云++郭新梅++辛淑亮

摘 要： 本文通过Excel首先对例题分别进行4个单因素完全随机试验数据的方差分析，然后进行联合方差分析。由此证明统计学中的“系统分组设计”或“巢设计”或“窝设计”，实质上就是几个单因素完全随机试验的联合方差分析。从理论上解决了重复次数不等的单因素完全随机试验，按照系统分组进行联合方差分析的问题。

关键词： 单因素 完全随机试验 联合方差分析 系统分组设计

根据重复和随机两个试验设计原则，所形成的完全随机设计，简单方便，广泛使用。在方差分析中误差的自由度最大，统计显著性要求的F临界值最小[1，2]。对于单因素完全随机试验可以单独进行方差分析；也可以把几个单因素完全随机试验联合进行方差分析，能够获得更多试验信息[3，4，5]。

例：在温室内以A、B、C、D 4种培养液培养玉米，每种3盆（浓度不同），每盆4株，一个月后测定其株高（cm），得结果如表1，作方差分析[2]。

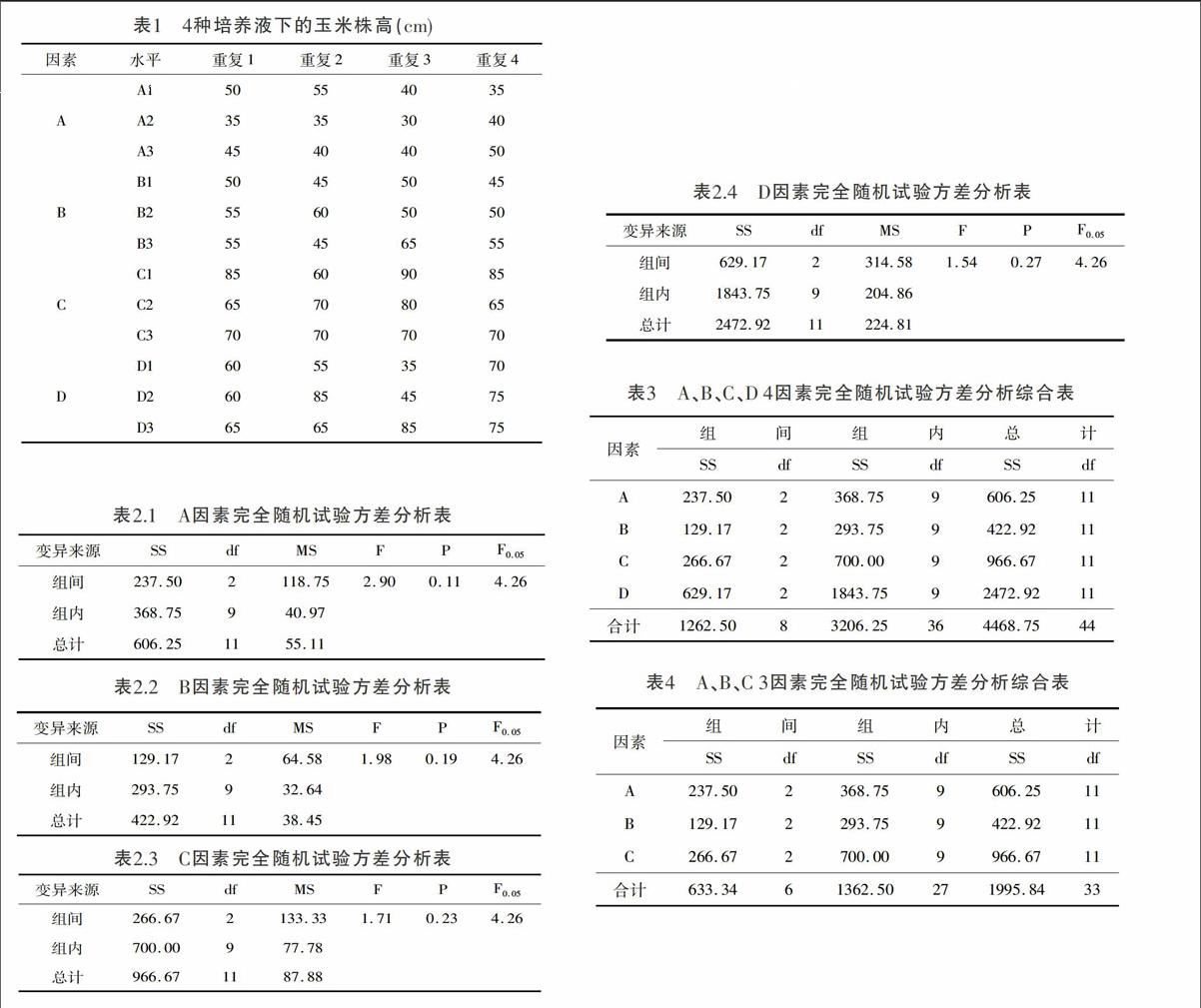
表1 4种培养液下的玉米株高（cm）

1.按照单因素完全随机试验进行方差分析

用Excel对A、B、C、D 4因素分别进行方差分析，结果于表2。

表2.1 A因素完全随机试验方差分析表

表2.2 B因素完全随机试验方差分析表

2.对4个单因素完全随机试验方差分析的结果进行综合

用Excel对A、B、C、D 4因素分别方差分析的结果，汇总于表3。

表3 A、B、C、D 4因素完全随机试验方差分析综合表

3.方差齐性检验

方差分析有一个假定，所有试验处理必须具有共同的方差。对表3总计项用bartlett法作方差齐性检验。

卡方值χ2=1.8216，概率P=0.4022

结论：因为实得概率P>α，故接受H0，认为各组间方差齐。因此，可以将上述A、B、C 3因素合并进行方差分析。

4.A、B、C 3因素合并资料的方差分析

4.1对合并资料进行方差分析

计算合并资料的总变异平方和SS=8388.89，自由度df=36-1=35。

处理间平方和SS=6393.06，自由度df=3-1=2。

4.2按照系统分组进行方差分析

把表4与合并资料的总变异、处理间变异加以综合，得到系统分组方差分析的结果于表5。

表5 A、B、C 3因素系统分组方差分析表

4.3平方和与自由度的关系式

表4总计平方和SS=1995.84；总计自由度df=33。表5总变异平方和SS=8388.89；总变异自由度df=35。处理（组）间平方和SS=6393.06；自由度df=2。

关系式：平方和SS=8388.89-1995.84=6393.06；自由度df=35-33=2。这是由于把A、B、C 3因素联合进行方差分析，增加了“新的变异来源”而增加的平方和与自由度。

5.结论与讨论

5.1几个单因素完全随机试验联合方差分析的步骤

①首先按照单因素完全随机试验分别进行方差分析；

②把几个单因素完全随机试验方差分析的结果加以综合；

③作方差齐性检验，剔除影响方差齐性最大的方差；

④对合并资料按照单因素完全随机试验进行方差分析；

⑤把②和④综合，得到系统分组方差分析的结果。

上述方法步骤，不仅适用于重复次数相等资料的单因素完全随机试验，而且适用于重复次数不等资料的单因素完全随机试验。

5.2证明现有系统分组设计方差分析的变异原因划分欠妥

统计学中所谓的“系统分组设计”或“巢设计”或“窝设计”，实质上就是几个单因素完全随机试验的联合方差分析，即一组相同试验方案数据的联合分析[2]。而且原来的系统分组设计方差分析时，“总变异=处理（组）间+组内亚组间+处理内”并不恰当，应该改为“总变异=因素间+因素内水平间+误差”，这样一来变异原因更加明确。以前所有的统计书都把系统分组设计作为一种特别的试验设计，必须澄清，应当改正。

参考文献：

[1]辛淑亮.现代农业试验统计[M].北京：中国统计出版社，1999.

[2]盖钧镒.试验统计方法[M].北京：中国农业出版社，2000：91，135，273.

[3]莫惠栋.农业试验统计[M].上海：上海科学技术出版社，1984.

[4]王钦德，扬坚.食品试验统计与统计分析[M].北京：中国农业大学出版社，2010：62.

[5]刘权.果树试验统计及统计[M].北京：中国农业出版社，1997.

基金项目：山东省应用型人才培养特色名校建设工程。

通讯作者：辛淑亮