基于加速遗传算法的方钢管混凝土柱优化模型
袁朝阳, 吴成国, 张宇亮, 钟磊, 杨齐祺
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
基于加速遗传算法的方钢管混凝土柱优化模型
袁朝阳, 吴成国, 张宇亮, 钟磊, 杨齐祺
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
方钢管混凝土柱因其优良的性能被越来越多地应用到高层建筑结构设计中,其经济性也日益受到关注。设计合理的构件尺寸将会节省投资成本、降低工程造价,因此合理地优化方钢管混凝土柱构件则显得非常重要。根据钢管混凝土结构设计最新规范建立方钢管混凝土柱优化模型,并采用罚函数法处理复杂约束问题,提出用加速遗传算法求解该优化模型,并以某高层结构底层柱为例进行了应用验证。结果表明:经加速遗传算法优化后的单根柱造价比原设计造价节省了24.5%,效益可观;用加速遗传算法对方钢管混凝土柱进行优化设计是可行的,具有较高的经济效益和推广应用价值。
方钢管混凝土柱;设计优化;加速遗传算法
钢管混凝土结构是将混凝土填充到钢管中的一种组合结构,自20世纪60年代以来,因其受力性能优越和钢材节省等显著优点而得到广泛应用[1-2]。目前,国内外使用较多的钢管混凝土组合构件形状是圆形和方形,其中方钢管混凝土结构因其构造简单、易于连接和耐火性好等优点越来越被工程界所重视[3-4]。随着高层框架结构中组合柱的广泛使用,钢管混凝土柱的经济性受到越来越多的关注,为降低工程成本而寻找高效的优化算法成为结构领域的热门研究方向。已有许多学者对结构构件的优化做了研究[5-7],但较多的是基于经验的简化计算过程,不能快速获得优化设计方案。随着人工智能和计算机的快速发展,对结构构件的复杂问题进行智能优化成为了一种新的趋势。遗传算法[8]作为一种能处理复杂优化问题的人工智能算法,近年来在结构构件优化领域中得到了广泛的应用。肖国涛[9]基于遗传算法构建了工字型钢梁的优化模型,结果证实了该方法对梁构件进行优化是有效的。时富禄[10]在2007年利用遗传算法对桥的工程施工进行了优化,大大提高了效率。张怀强等[11]在2009年利用遗传算法对给水管网进行了优化设计,避免了管径的调整,快速得到了最优设计方案。2011年刘晓峰[12]建立了桩基础遗传优化模型,并举例进行计算,验证了遗传算法在桩基础优化中的可行性。聂相田等[13]在2013年将遗传算法应用到监理巡视路线的优化当中,并对南水北调一期工程巡视路线进行了优化设计,取得了较好的效果。同时,金菊良等[14]将标准遗传算法经多次迭代后所产生的优秀个体的变量变化区间作为优化变量新的初始变化区间,由此得到对标准遗传算法进行改进后的方法——加速遗传算法(Accelerating Genetic Algorithm,AGA)。在上述研究的基础上,本文将加速遗传算法应用到方钢管混凝土柱的优化中,根据方钢管混凝土柱的最新设计规范和相关研究[15-18]来构建优化模型,并举例验证了该模型用于方钢管混凝土柱的可行性和经济性。
1 加速遗传算法
1.1 基本原理
遗传算法是模拟自然界中优胜劣汰的规则并随着仿生学不断发展而形成的人工智能优化方法[8]。它遵循着生物进化的基本规律,在高维空间不断寻优,借鉴生物学中的繁殖、遗传、变异等遗传操作,且遵循优胜劣汰的法则,保留比较优秀的个体,淘汰不够优秀的个体,进而逐步逼近所要找的最优个体。
标准遗传算法[14]是国内外较为常用的算法,在解决各种优化问题时做出了较大的贡献。但是该方法在运算当中也存在很多的缺点,如容易出现过早收敛、优化速度比较慢、随着迭代次数的增加寻优效率会大大降低等。针对存在的这些问题,金菊良等[14]在标准遗传算法的基础上进行了改进,提出了加速遗传算法(AGA)。加速遗传算法不仅继承了标准遗传算法适应性强、全局优化、通用等特点,而且在原方法的基础上显示出计算量少而精度高等优点[14],其算法结构如图1所示。
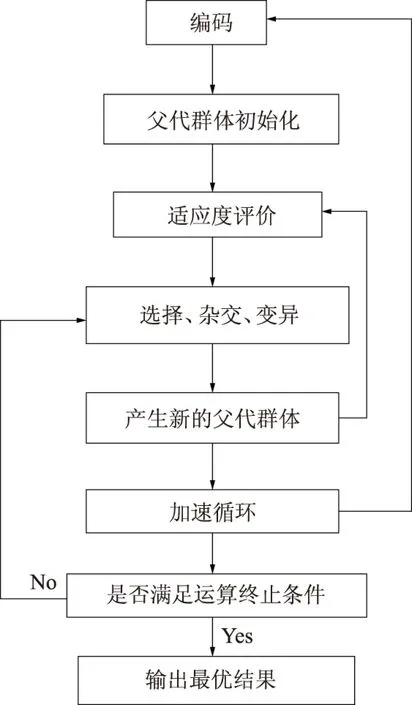
图1 加速遗传算法计算流程
1.2 基于加速遗传算法的结构优化思路
采用加速遗传算法对结构进行优化,目标函数值和优化变量设定如下:
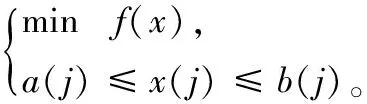
(1)
式中:f(x)为目标函数;x(j)为第j个变量值;a(j)、b(j)分别为第j个变量的变化区间的下限和上限。
针对算法当中的编码方式、适应度评价方法、选择、杂交及变异等重要步骤作如下分析:
1)编码方式。考虑到效率高的优点,采用实数编码的方式,即对优化变量作如下线性变换[8]:
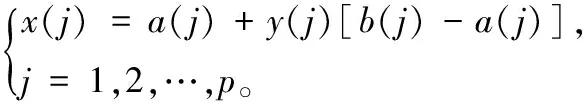
(2)
式中y(j)为第j个优化变量对应到[0,1]区间上的实数值。
2)适应度评价方法。以目标函数值越小越好为基准,当目标函数值f(i)(i=1,2,…,n)越小时,说明个体的适应度值越高。第i个个体的适应度值F(i)可用下式计算[8]:
F(i)=1/[f(i)f(i)+0.001]。
(3)
式中的“0.001”是经验设置的,是为了避免出现目标函数值为0而导致分母为0的情况。
3)选择。计算得到适应度值后,按比例选择方式计算选择概率[8]如下:
(4)
式中:ps(i)为父代个体的选择概率;p(i)为累加概率,通过将变量区间分成区段与父代个体一一对应来选择。
4)杂交。根据上式的选择概率随机选择1对父代个体y(j,i1)与y(j,i2)作为双亲,并作如下线性组合得到新的个体y2(j,i)[8]:
(5)
式中u1,u2,u3都是[0,1]区间上的随机数。
5) 变异。变异的目的就是为了增强群体的多样性。当目标函数值f(i)越小时,选择概率ps(i)也就越小,对个体进行变异的概率pm(i)应越大。因此,基于实数编码的加速遗传算法变异操作如下[8]:
(6)
式中:变异概率pm(i)=1-ps(i);y3(j,i)为y(j,i)变异后的个体;u(j)和um均为[0,1]区间上的随机数。
以上为利用加速遗传算法对结构进行优化的编码、遗传操作等主要步骤的介绍,根据上述主要步骤及加速遗传算法流程可对建立的方钢管混凝土柱优化模型进行求解。
2 优化模型设计
2.1 设计要求分析
方钢管混凝土柱属于高层建筑结构的主要承重构件,近年来随着建筑结构的高层化,方钢管混凝土柱的使用量也在不断加大。由于柱子在整个工程造价中所占的经济比重相对比较大[15-16],因此,在结构设计当中,若能在满足稳定承载力的前提下合理缩小柱子的尺寸,将会大大降低工程投资的成本,产生较大的经济效益。方钢管混凝土柱的截面如图2所示。
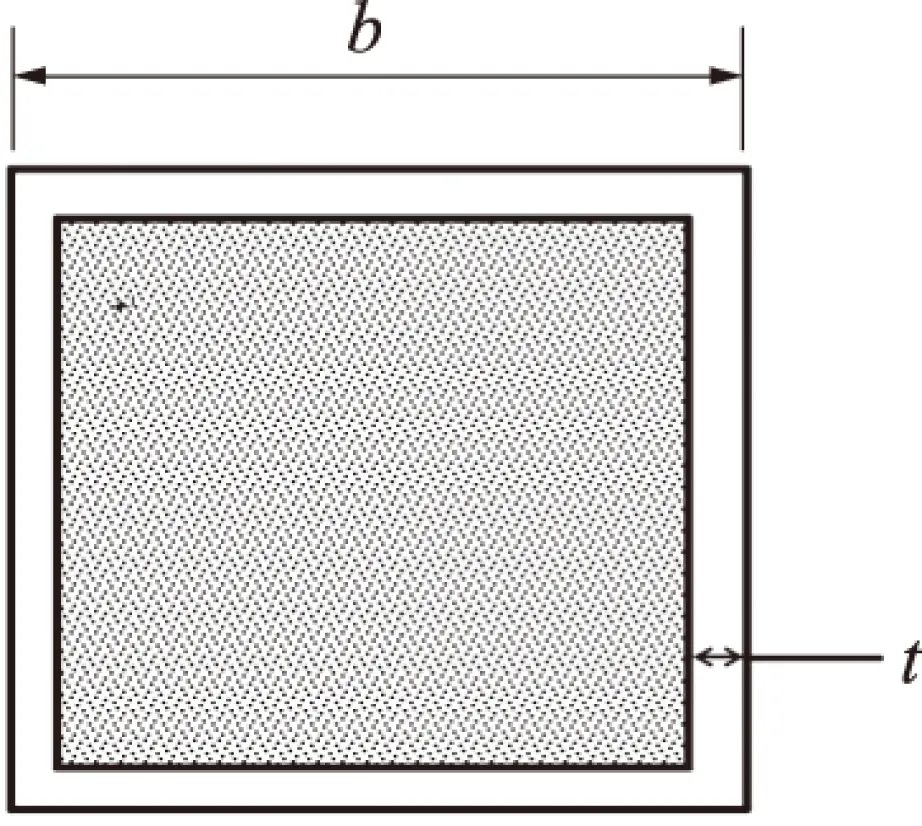
图2 方钢管混凝土柱截面示意图
以单根钢管混凝土承重柱的造价为目标函数,以“设计变量尽可能少”为原则确定优化变量为截面直径b和钢管壁厚t,建立目标函数如下:
F(b,t)=4Cs(bt-t2)L+Cc(b-2t)2L。
(7)
式中:Cs为钢材的单位体积造价,元/m3;Cc为混凝土单位体积造价,元/m3;L为柱子的有效长度,m;b为截面直径,mm;t为钢管壁厚,mm。材料造价具有较大的模糊性,可按预算定额取值,且不同的钢材和混凝土造价会对目标函数有所影响,因此,在应用当中,应根据不同工程选用实际的材料价格。
根据方形钢管混凝土柱轴心受压承载力计算公式和最新设计规范[16-18]的要求确定约束条件如下:
强度条件
Nu≤N0=Ascfysc,
(8)
稳定性条件
Nu≤φN0,
(9)
宽厚比
(10)
套箍系数
0.5<ξ<2,
(11)
含钢率
6%<α<10%,
(12)
工程要求
b≥100,t≥4。
(13)
其中
fysc=(1.212+Bξ+Cξ2)fc,
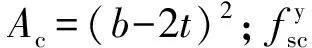
2.2 优化模型建立
方钢管混凝土柱的优化目的是在满足正常使用的前提下,寻找最优的尺寸设计方案,使成本降到最低。据此可通过上述目标函数和约束条件建立优化模型:
minF(b,t)=4Cs(bt-t2)L+Cc(b-2t)2L,
(14)
(15)
对于有约束条件的问题,工程中常通过惩罚不可行解来处理。惩罚的策略主要是通过设计惩罚函数将有约束问题转化为无约束问题,进而用无约束优化方法来求解。构造惩罚函数的形式常用的有乘法和加法[19]。考虑到目标函数值较小,采用加法就可以取得良好的效果,因此本文采用加法的形式构造惩罚函数,将式(14)改写为无约束形式:
(16)式中hi[gi(b,t)]为罚项。当满足约束条件gi(b,t)(i=1,2,…,6)时罚项取值为0;不满足该约束条件时,取一足够大的正实数M。因此,可以用AGA来解这类非线性优化问题,f即为新的目标函数。
3 实证研究
某工程底层承重结构柱采用方形钢管混凝土柱,如图3所示,设计柱的截面尺寸为400 mm×400 mm,钢板厚度为10 mm,柱子有效长度为4.5 m。钢板采用Q235级钢,屈服强度和设计强度分别为235、215 N/mm2。混凝土强度等级为C40,抗压强度标准值和设计值分别为26.8、19.1 N/mm2。该承重柱的设计最大轴力为5 000 kN。钢材的预算定额取29 516元/m3,混凝土预算定额取378元/m3。

图3 方钢管混凝土柱
根据基础数据可计算得影响系数B、C分别为0.854和-0.0676;套箍系数ξ为1.216;稳定性系数φ经查表取为0.858;当钢材为Q235时组合强度值须乘以系数0.96[16],计算组合柱的组合强度值为39.4 N/mm2。
设计群体规模为300,优秀个体数为20,杂交概率为100%,终止代数为30。根据前述加速遗传算法的原理及流程,通过MATLAB软件编制基于实数编码的加速遗传算法程序,根据式(15)中约束条件7和8设置变量初始区间分别为b[100,1 000],t[4,15],M取为107,用加速遗传算法解目标函数式(10)和约束条件7和8组成的优化模型对该单根方钢管混凝土柱进行优化计算。与普通结构优化设计方法相比,智能优化获得最优解的速度大大提高,且通过加速遗传算法对模型优化的速度高于标准遗传算法,本例通过加速遗传算法得到优化结果只需0.687 s,标准遗传算法则需要0.935 s,且容易局部收敛。加速寻优30次后得到的最优解与原设计值的对比结果见表1。

表1 优化设计结果
由表1可知,经优化后的设计与原设计相比,方钢管混凝土柱的直径几乎没有变化,但含钢率大大减小,同时,柱子造价比原设计降低了24.5%,说明含钢率对柱子材料造价的影响较大。经优化后的柱子最大承载力为5 830 kN,大于最大轴力设计值5 000 kN,承载力满足条件。表明本文通过加速遗传算法求解的钢管混凝土柱优化模型具有较高的经济性且应用方便,该方法可应用到实际工程当中,将会为工程预算提供有效参考。
4 结 语
工程领域中的各种复杂非线性问题已成为结构优化的难点,方钢管混凝土柱作为高层建筑结构的常用构件,其截面优化设计也日益受到关注。本文采用钢管混凝土结构设计最新规范构建了方钢管混凝土柱的优化模型,并编制加速遗传算法程序对该优化模型进行求解。在满足规范要求的前提下,通过改变柱子的宽度和钢板厚度使造价降到最低,优化后结果与原设计相比,单根柱的造价大大降低,具有较高的经济效益和社会效益。加速遗传算法用于优化的优点是计算速度快、全局搜索能力强,优化模型建立较为简单,处理各种工程实际优化问题较为方便。目前加速遗传算法在组合结构优化设计领域应用还不够广泛,具有较大的发展空间。当前的研究主要是针对单工况荷载下的优化,而实际工程中的结构则受到各种复杂的荷载作用,其构件也是由多种材料组合而成,如何将加速遗传算法更好地应用到实际工程当中,还有很多的研究工作要做。
[1]韩林海.钢管混凝土结构:理论与实践[M].北京:科学出版社,2007:5-26.
[2]胡利,王春磊,李锋宁.钢-混凝土组合结构的研究进展[J].华北水利水电学院学报,2009,30(2):51-53.
[3]Schneider S P.Axially loaded concrete-filled steel tubes[J].Journal of structural Engineering,1999,125(10):1202-1206.
[4]汤义鹏,郭艳坤.钢-混凝土组合结构构件工作性能的研究进展[J].华北水利水电学院学报,2010,31(4):46-49.
[5]Chai S,Sun H C.A relative difference quotient algorithm for discrete optimization[J].Structural Optimization,1996,12(1):46-56.
[6]Han L H.Tests on stub columns of concrete-filled RHS sections[J].Journal of Constructional Steel Research,2002,58(3):22-27.
[7]Shams M,Saadeghvaziri M A.State of the art of concrete-filled steel tubular columns[J].Aci Structural Journal,1997,94(5):558-571.
[8]金菊良,杨晓华,丁晶.基于实数编码的加速遗传算法[J].四川大学学报(工程科学版),2000,32(4):20-24.
[9]肖国涛.基于遗传算法的钢管混凝土框架结构研究[D].武汉:华中科技大学,2005:40-45.
[10]时富禄.基于遗传算法的大跨度钢桁拱桥施工优化研究[D].武汉:华中科技大学,2007:8-22.
[11]张怀强,张利伟,杜军虎,等.遗传算法在给水管网优化设计中的应用研究[J].华北水利水电学院学报,2009,30(1):21-22.
[12]刘晓峰.自动分组遗传算法的改进及在结构工程中的应用[D].大连:大连理工大学,2011:50-66.
[13]聂相田,郑良,纪园可,等.基于遗传算法的监理巡视线路优化[J].华北水利水电学院学报,2013,34(6):54-56.
[14]金菊良,杨晓华,丁晶.标准遗传算法的改进方案:加速遗传算法[J].系统工程理论与实践,2001(4):8-13.
[15]郑新志.薄壁方钢管混凝土柱劲化设计及轴压性能探讨[J].华南地震,2014,34(1):94-102.
[16]陈世鸣.钢-混凝土组合结构[M].北京:中国建筑工业出版社,2012:151-166.
[17]韩林海,陶忠.方形截面钢管混凝土构件的设计计算[J].钢结构,1998(4):39-45.
[18]哈尔滨工业大学.实心与空心钢管混凝土结构技术规程:CECS 254:2012[S].北京:中国计划出版社,2013:9-20.
[19]胡一波,王宇平.解约束优化问题的一种新的罚函数模型[J].计算机科学,2009,36(7):240-243.
(责任编辑:陈海涛)
The Optimization Model of Concrete-filled Square Steel Tubular Columns Based on Accelerating Genetic Algorithm
YUAN Chaoyang, WU Chengguo, ZHANG Yuliang, ZHONG Lei, YANG Qiqi
(College of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)
Concrete-filled square steel tubular columns were applied in the design of high-rise building structure increasingly because of the good performance, and their economy was also paid more and more attention. It will save the investment cost and reduce the cost of projects if the components are designed reasonably. Therefore, the reasonable optimization of the components is very important. In this paper, the optimization model of concrete-filled square steel tubular columns was established based on the latest design standard of concrete-filled steel tubular structure, the penalty functions were utilized to deal with the complex constraint problems, it was put forward that the optimization model could be solved with accelerating genetic algorithm program, the application research was done according to the bottom columns of a high-rise building. Results show that the cost of a single column optimized with accelerating genetic algorithm method will be reduced 24.5% compared to the original design, the benefit is considerable; so it is feasible to optimize and design the concrete-filled square steel tubular columns with accelerating genetic algorithm, which also has high economic efficiency and popularization value.
concrete-filled square steel tubular column; design optimization; accelerating genetic algorithm
2016-01-13
国家自然科学基金项目(51309072,51309004)。
袁朝阳(1990—),男,河南驻马店人,硕士研究生,主要从事水资源工程与结构研究。E-mail:912779797@qq.com。
吴成国(1982—),男,甘肃民乐人,讲师,主要从事水资源系统工程研究。E-mail:wule9825@163.com。
10.3969/j.issn.1002-5634.2016.02.010
TV335;TU318
A
1002-5634(2016)02-0057-05

