基于数学形态滤波的调制方式识别

陈　静，杨　明

(中国人民解放军91404部队，河北 秦皇岛 066001)



基于数学形态滤波的调制方式识别

陈静，杨明

(中国人民解放军91404部队，河北 秦皇岛 066001)

摘要：简要介绍了数学形态滤波的基本原理与形态滤波器的构建，针对通信信号中存在的加性高斯白噪声问题，提出了一种运用数学形态滤波方法对信号瞬时包络进行整形滤波，再提取相应的特征参数J进行调制样式识别的新方法。并将该方法用于对2ASK、4ASK、QPSK、8PSK和2FSK等信号的识别中，实验结果表明，该方法对高斯白噪声有很好的滤波效果，亦表明数学形态滤波在通信领域有很好的应用前景。

关键词：数学形态滤波；调制样式识别；加性高斯白噪声；高阶累积量

0引言

通信信号调制样式识别一直是非协作通信信号截获的主要问题，由于电磁环境日益复杂，非协作通信接收信号的信噪比越来越低，对信号的调制识别以及后续的解调处理产生了很大的不利影响，所以有必要抑制信号中的噪声，整形滤波是抑制噪声的一种方法。

传统的线性滤波器不能有效地去除各种同频噪声，如高斯白噪声具有很宽的频带，信号的频率成分和噪声、干扰的频率重叠在一起，致使常用的数字滤波器无法将两者区分开来，而部分非线性滤波器可以有效地去除同频噪声并保留原信号的特征。

1数学形态滤波

数学形态滤波器是一种非线性滤波器，是数学形态学在信号处理领域的一个应用。数学形态学以集合论、积分几何为数学理论基础，提供了基于形状的变换理论和方法。数学形态滤波与传统的滤波和变换理论不同，它是一种关于信号形状的非线性滤波和变换。

利用数学形态滤波器，信号的形状信息可以通过选择合适的结构元素采用数学形态学变换的方法进行提取和处理。由于数学形态滤波器具有良好的滤波性能，使得它在一维时域信号的处理中也得到了人们的重视[1,2]。

数学形态学用集合来描述目标信号，在进行信号处理时设计一个称为结构元素的“探针”，通过该探针在信号中的不断移动，便可提取有用的信息做特征分析和描述。形态变换构成简单，其基本运算为膨胀、腐蚀、形态开运算、形态闭运算，以及形态开、闭的级联组合。通过不同的组合，就可形成丰富多彩的算法和信号处理系统[3]。

设f(n)为定义在F={0,1,2,…,N}上的离散信号，B为一集合，称为结构元素。则f(n)关于集合B的膨胀运算、腐蚀运算定义如下[4]：

膨胀运算

(f⊕B)(n)=max{f(n-m); (n-m)∈F,m∈B}；

腐蚀运算

(f⊖B)(n)=min{f(n+m); (n+m)∈F,m∈B}。

很明显，(f⊕B)(n)≥(f⊖B)(n)。膨胀运算和腐蚀运算分别是关于结构元素B(n)的最大和最小运算，它们是递增的、位移不变的，并且是一种并行局部运算。利用膨胀运算、腐蚀运算，能组合成更为复杂的形态变换，如形态开、形态闭、形态开-闭、形态闭-开、多结构元素形态变换等等。

形态开：

(f∘B)(n)=(f⊖B⊕B)(n)；

形态闭：

(f·B)(n)=(f⊕B⊖B)(n)；

形态开-闭：

(f∘B·B)(n)=((f⊖B⊕B)⊕B⊖B)(n)；

形态闭-开：

(f·B°B)(n)=((f⊕B⊖B)⊖B⊕B)(n)。

由上可知，

形态开、形态闭是复合的极值滤波运算。它们不仅是递增的、位移不变的，而且具有等幂性，即：

(f·B·B)(n)=(f·B)(n)，

(f∘B∘B)(n)=(f∘B)(n)。

形态滤波器的等幂性是其他非线性滤波器和线性滤波器所不具备的，它意味着信号经过一次形态滤波后不再为相同的形态滤波运算所改变，明确了这一性质，可以避免进行无谓的重复工作。

由于噪声表现为信号上叠加窄的“毛刺”，即很尖“峰”和很低“谷”，开运算可以分离过滤比结构元素小的孤立部分，削去其“峰”，闭运算可以补缺填充比结构元素小的孤立部分，填平其“谷”。因此在实际应用中，针对通信信号噪声特征可以采取开、闭运算或其组合级联运算等去除噪声。

这种组合级联不是完全地删除波形中的最大峰和最低谷，而是对其进行有效的压缩。因为形态开保持了波形的低谷，但删除了正峰；而形态闭则保持了波形的正峰，但删除了低谷。

2数学形态滤波性能仿真

本文定义2个结构元素：S1(n)(n∈S1)、S2(n)(n∈S2)且S1⊂S2，则形态开-闭Foc(f)和形态闭-开Fco(f)滤波器分别定义为：

Foc(f)=f(n)∘S1·S2，

Fco(f)=f(n)·S1∘S2。

组合形态滤波器的输出：

y(n)=[Foc(f)+Fco(f)]/2。

(1)

其中，结构元素形状和大小对形态学运算产生很大的影响。结构元素的形状、宽度和高度决定了结构元素的特征，结构元素的长度要小于信号的最小周期。常用的结构元素有直线、曲线、圆形以及其他多边形。相对而言，结构元素越复杂，其滤除信号的能力就越强，但所耗费的时间也越长。输出波的形状决定了结构元素的值。实际运算中，结构元素的设计取决于待处理信号的形状[3]。

对于通信信号中的加性高斯白噪声，通过大量仿真分析可知，菱形和圆形的结构元素处理滤波效果较好。

运用式(1)构造开-闭和闭-开组合形态滤波器，结构元素S1(n)(n∈S1)选为菱形，S2(n)(n∈S2)选为圆形，处理图1(a)的正弦信号中的加性高斯白噪声。Matlab算例中2个结构元素的大小均选为2,处理结果如图1(b)所示。

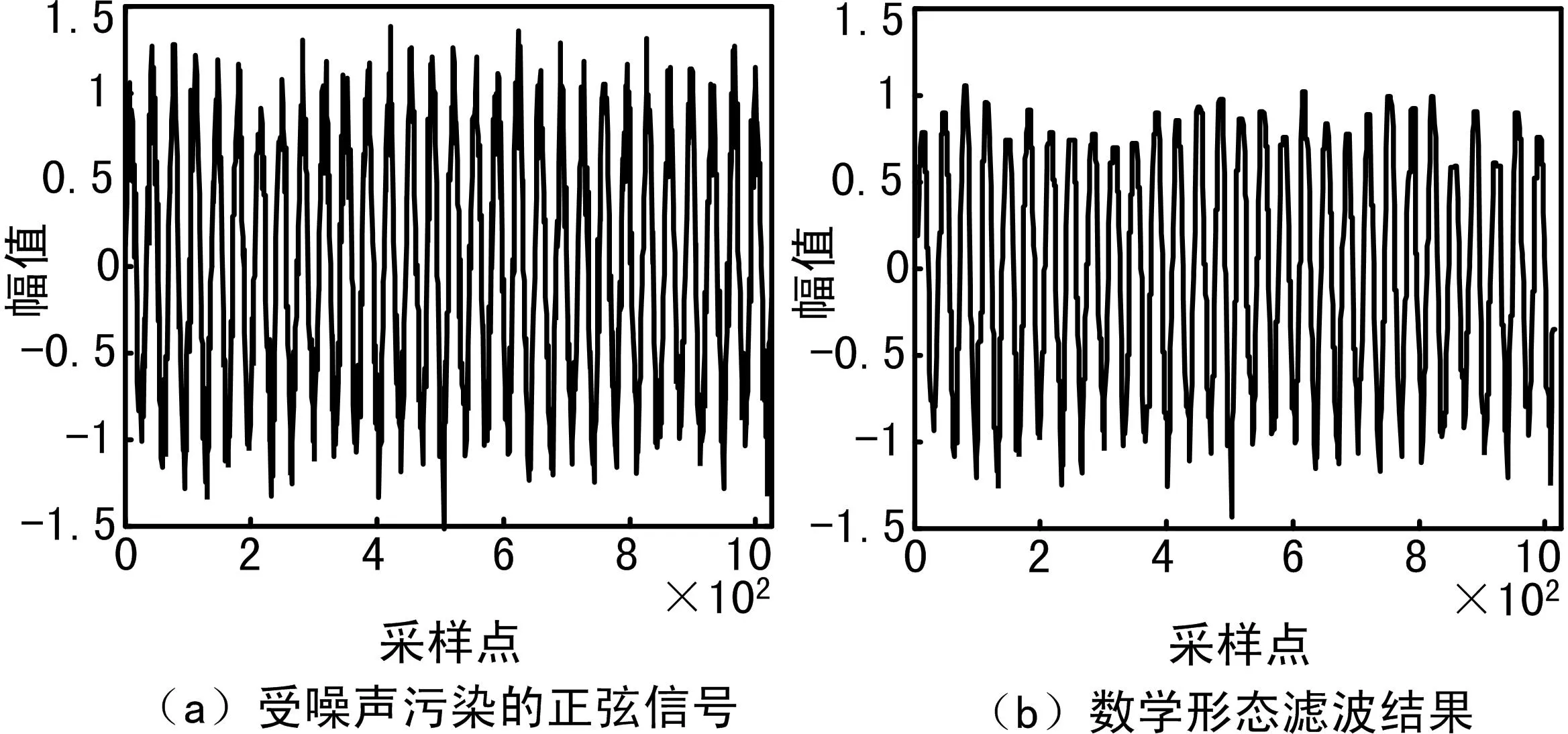
图1　数学形态滤波示意图

从图1可以看出，数学形态滤波在消除加性高斯白噪声方面有一定的效果。

3特征参数提取

提出了一种应用高阶包络[4,,5]和高阶累积量计算的高阶特征参数J、s1和s2来识别QPSK、8PSK、2ASK、4ASK和2FSK信号的方法。

重点介绍高阶包络特征J，其定义为：

(2)

其推导过程如下[5]：

接收信号可以表示为已调信号与噪声之和，即：

y(t)=s(t)+n(t)，

s(t)可表示为：

s(t)=a(t)cos[φ(t)]，

φ(t)=2πfct+θc。

从而接收信号的瞬时包络ξ(t)的二、四阶矩分别为：

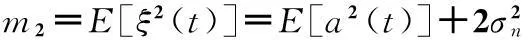
(3)

m4=E[ξ4(t)]=E{[a2(t)+2a(t)A(t)+c2(t)]2}，

(4)

式中，

利用高斯白噪声的特性和信号与噪声不相关的假设可以简化式(4)为：

(5)

结合式(3)和式(5)可得：

m4-2(m2)2=E[a4(t)]-2E2[a2(t)]。

(6)

c42为已调信号s(t)的四阶累积量，定义为：

(7)

式中，

(8)

(9)

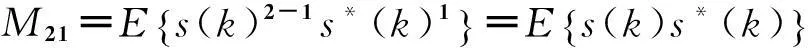
(10)

分别为s(t)的四阶矩和二阶矩。其中，s*(t)为s(t)的共轭。

综合式(6)、式(7)和式(2)即可求得特征参数J的值。

利用特征参数J可以将待识别信号分为3类：{QPSK、8PSK}、{2ASK、4ASK}和{2FSK}。

然后，对于QPSK、8PSK两类信号，可以进一步应用高阶累积量特征参数s1分开。而2ASK、4ASK两类信号可以选用高阶累积量特征参数s2分开。

特征参数s1定义为：

(11)

特征参数s2定义为：

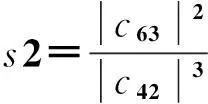
(12)

4仿真实验

下面首先利用数学形态滤波方法对接收信号的瞬时包络滤波整形[7]，然后再利用上述方法提取识别特征参数J实现调制样式的识别。采用蒙特卡洛试验方法进行仿真。

仿真参数设为：载波频率fc=150kHz，符号速率fb=12.5kHz，采样速率fs=1.2MHz，信号长度为1 024。

图2中描绘的是正确识别概率(Pc)随着SNR的不同而变化的关系，给出了2ASK、4ASK、QPSK、8PSK和2FSK的识别性能。

图2　通信信号的正确识别率(经过数学形态滤波)

从图中可以看出，在SNR为4 dB时，各类信号的正确识别概率均在95%以上，从而证明了该算法的可行性。

而没有采用数学形态滤波方法对瞬时包络进行滤波时，各类信号的正确识别概率在SNR为4 dB时比所提出的新方法的性能差，如图3所示。

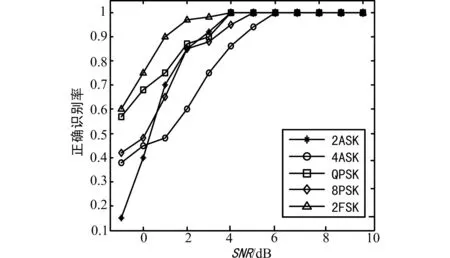
图3　通信信号的正确识别率(未经过数学形态滤波)

5结束语

利用数学形态滤波方法对瞬时包络进行滤波，然后基于瞬时包络提取一种特征参数J对2ASK、4ASK、QPSK、8PSK和2FSK信号识别，并通过算法的仿真对识别性能进行了研究。仿真实验结果表明形态滤波能够在消除信号中高斯噪声的同时保留真实信号的实际特征，使得利用瞬时包络特征参数进行调制方式识别的算法能够在SNR较低时达到较高的正确识别概率。

参考文献

[1]Hemdal J F,Lougheed R M.Morphological Approaches to the Automatic Extraction of Phonetic Features[J].IEEE Transactions on Signal Processing,1991,39(2):490-497.

[2]Trahanias P E.An Approach to QRS Complex Detection Using Mathematical Morphology[J].IEEE Trans Biomed Eng,1993,40(2):201-205.

[3]李春枝，何荣建，田光明.数学形态滤波在振动信号分析中的应用研究[J].计算机工程与科学，2008，30(9)：126-127，131.

[4]唐常青，吕宏伯，黄 铮,等.数学形态学方法及其应用[M].北京：科学出版社，1990.

[5]Mitra K S. Digital Signal Processing——A Computer-based Approach(Second Edition)[M].孙洪，余翔宇,译.北京：电子工业出版社，2006：34-169.

[6]Cai Quanwei ,WeiPing,Xiao Xianci.A Digital Modulation Recognition Method[C]∥2004 International Conference on Communications Circuits and Systems,2004,2:863-866.

[7]Fan H B,Chen J,Cao Z G.An Algorithm of SNR Estimation for Non Constant Envelope Signal in the Awgn Channel[J].Acta Electronica Sinica,2002,30(9):1369-1371.

[8]秦襄培.MATLAB图像处理与界面编程宝典[M].北京：电子工业出版社，2009.

Modulation Recognition Based on Mathematical Morphology Filtering

CHEN Jing,YANG Ming

(Unit 91404,PLA,Qinhuangdao Hebei 066001,China)

Abstract：This paper briefly introduces the basic principle of mathematical morphology filtering and the construction of morphology filter.In view of advanced Gaussian white noise in communication signal,a new modulation recognition method is presented.This method uses mathematical morphological filtering to implement shaping filtering for signal instantaneous envelope,and then extract corresponding feature parameter J for modulation recognition.This method is used in recognition of such signals as 2ASK,4ASK,QPSK,8PSK and 2FSK.The experimental results show that this method has higher filtering effect for Gaussian whiter noise,and the mathematical morphology filtering has better application prospect in communication field.

Key words：mathematical morphology filtering;modulation recognition;AGWN;high-order comulants

作者简介：陈静(1975—)，女，高级工程师，主要研究方向：通信与通信对抗。杨明(1975—),男，高级工程师，主要研究方向：通信与通信对抗。

收稿日期：2015-09-15

中图分类号：TN911

文献标识码：A

文章编号：1003-3114(2016)01-54-3

doi:10.3969/j.issn.1003-3114.2016.01.14

引用格式：陈静，杨明.基于数学形态滤波的调制方式识别[J].无线电通信技术,2016,42(1):54-56，64.