单个气泡上浮过程的数值模拟
张 妍杨 帆,2
(1.上海理工大学 能源与动力工程学院,上海 200093;
2.上海理工大学 上海市动力工程多相流动与传热重点实验室,上海 200093)
单个气泡上浮过程的数值模拟
张 妍1杨 帆1,2
(1.上海理工大学 能源与动力工程学院,上海 200093;
2.上海理工大学 上海市动力工程多相流动与传热重点实验室,上海 200093)
为了了解气泡上浮过程中形态的变化,采用FLUENT软件中“流体体积”(Volume of Fluid,VOF)模型对单个气泡在静止液体中的上浮情况进行数值模拟,得到了奥特斯数(Eo)在O(10-1)~O(102),莫顿数(Mo)在O(10-9)~O(104)范围内气泡的形态。将计算得到的结果与气泡形状图谱做对比,印证了无量纲参数Eo数、Mo数和Re数的数值大小与气泡在上浮过程中形状的变化和最终速度密切相关。
气泡上浮 VOF 数值模拟 气泡形状
引言
气液两相流广泛存在于人类的生产、生活等各个领域。其中,气泡的产生及特性对船舶运输、石化工业、食品、医疗以及能源的开发和利用都有着重要的影响。对气泡的形状和运动特性的掌握,对生产过程中的参数设定、控制运行以及生产效率的提高等方面起着重要的作用。
国内外学者对气泡上浮过程中的形态变化、速度变化、受力情况、破碎现象以及气泡融合等现象做了大量研究。1959年,Young等[1]采用线性模型模拟研究了小雷诺数下气泡和水滴的移动。1976年,Grace等[2]人给出了著名的气泡形状图谱,提出了三个无量纲数奥特斯数(Eo)、莫顿数(Mo)、雷诺数(Re),以表征气泡在黏性溶液中的上升形态。Bhaga和Weber[3]接着完善了气泡图谱。此外,Li等[4]运用VOF(Volume of Fluid)法模拟了气泡在液体中的形成和上升。付攀等[5]对微小气泡的运动进行了仿真计算,并推导了运动方程。除了模拟方法之外,高速摄影也是主要采用的研究方式。例如,张建生等[6]运用高速摄影技术研究了气泡在水中的运动规律;郭容等[7]采用高速CCD成像技术实验,研究了气泡在不同黏度溶液中的上升速度和形状变化。
气液两相流中对相界面的追踪是研究重点。目前,追踪界面的方法主要有VOF法、level set法和Front Tracking等。其中,VOF方法是Hirt和Nichols[8]于1981年提出的。此种方法是在流场网格中定义某一种流体的相函数F,若其值为1,则说明此种流体完全占据网格,流体体积与网格体积之比为1;若其值为0,则表示网格内没有此种流体。相界面处网格内有多相流体,因此取值为(0,1)。确定相函数F值为0到1的网格位置,即可实现对相界面的追踪。VOF法计算量小、模拟精度高且容易实现,所以本文采用VOF方法来模拟静止黏性液体中单个气泡上升过程中形态变化等特性。
1 计算模型与方法
1.1 控制方程
本研究首先做以下几点假设:(1)所模拟多相流等温绝热,不与外界发生热交换;(2)气体和液体均是不可压缩牛顿流体;(3)由界面所分隔的两相流体为单相的流体系。此时,不可压缩黏性流体的控制方程为:
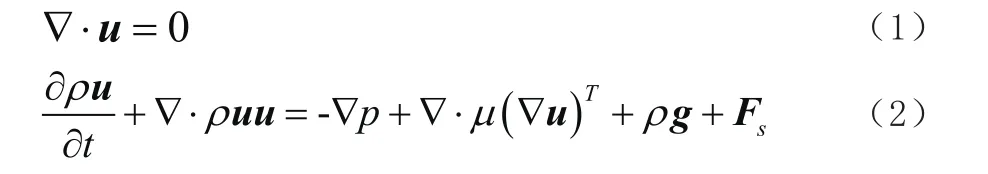
式中,u为流体的速度;ρ为流体密度;t为时间;p为压强;µ为流体的动力黏度;Fs为流体所受表面张力。
根据质量守恒,得到相界面的运动所满足输运方程为:

1.2 计算区域及网格
使用CFD前处理软件ANSYS ICEM,建立模拟模型为底边长0.08m,高0.2m的矩形区域。经拓扑后建立完整的模型,模型两边为固壁,上边界和下边界为周期性边界条件。整个矩形区域内充满液体,液体内部有一直径为0.02m的圆形气泡。图1为模拟计算模型示意图。

图1 计算模型示意图

图2 网格示意图
计算区域采用四边形单元进行离散,允许的最大网格尺寸为0.08。网格节点数为25219,网格数为25010。图2所示为网格示意图。
1.3 计算方法
模拟采用非稳态基于压力的VOF两相模型进行计算。重力加速度设为铅锤向下的9.8m/s2。采用PISO算法实现压力与速度的耦合。非稳态项采用一阶隐式时间推进法处理,计算时间步长为0.1×10-3s,时间步数为20000。
1.4 气泡运动概述
气泡在上升过程中主要受到重力、曳力、表面张力等各种作用力,其综合作用决定了气泡的形状。各作用力的相对大小可以用Eo数、Mo数和Re数表征。
Eo数表征重力与表面张力的比值,定义如下:

其中,g为重力加速度,m/s2;Δρ为液体与气体的密度差,kg/m3;dc为气泡当量直径,m;σ为表面张力系数,N/m。
Mo数表征连续相的物理性质,突出了粘度的影响。定义如下:

其中,lµ为液体的动力粘度,Pa·s;lρ为液体的密度,kg/m3。
Re数表征惯性力与粘性力的比值,定义如下:

其中,v为气泡稳定后的最终速度,m/s。
2 计算结果与分析
本文首先选取了五组Eo数和Mo数,给定一个密度差分别计算了各对应参数,并根据计算所获得的气泡最终速度,确定该工况所对应的Re数。计算参数如表1所示。

表1 计算工况
2.1 A4工况下气泡上升过程中形态的变化
图3(a)-(f)表示的是A4工况(即Eo=5.21×101,Mo=1.45×10-4)气泡上升中几个典型的形状变化图。在质量力作用下,气泡在上浮初期如图3(b)所示,由下边界中心点处向内凹陷,凹陷区域随着上浮过程不断增大,气泡形状越来越扁。从图4(e)可看出,气泡上升到一定程度后,凹陷处开始变平坦,气泡稍微变厚直至气泡稳定,最终保持球帽形匀速上升。这一过程是气泡所受各力平衡的过程。气泡所受的浮力、重力、曳力和表面张力是影响气泡上升过程中形状变化和速度的重要因素。所受重力基本不变,其他三个力随着气泡上浮的位置、速度的大小等逐渐变化而达到平衡。Mo数较小(黏度较小)、Eo数较大(表面张力较小)而难以维持气泡的初始圆形形状,最终变成下边界水平的球帽形。
2.2 A4工况下气泡上升过程中的流线变化

图3 A4工况气泡上浮形状变化图
图4中(a)-(f)为A4工况下气泡上浮流线变化过程。为便于观察流线与气泡的相对位置,图中只标示出左半部分,而右半部分与之对称。由图可直观观察到气泡从静止开始逐渐变形过程中气泡的回流现象。
如图4所示,(a)、(b)图为气泡运动初期,周围很快形成涡旋。上边界和下边界形成一个压力差而推动气泡上浮。随着气泡的上升涡旋不断增大,气泡下部向内凹陷程度越大。到达一定程度后,回流涡旋不再增大,气泡下边界逐渐平坦,最终气泡形状基本不变,以匀速垂直上浮。

图4 A4工况气泡上浮流线图
2.3 计算结果在图谱上的分布
图5为气泡形态图谱简图以及计算工况在图谱上的分布。图谱被划分为三个区域,即球形区、椭球形区和球帽形区。所计算工况A1、A2分布在椭球形区,可以看出,Mo数和Eo数较小、Re数较大时(A2),较难维持球形而变得更扁。这是由于液体黏度小,阻止气泡的变形能力较差,从而使得气泡变得更扁。相反,液体黏度较大时,气泡较易维持球形而更圆。工况A3分布在球形区,上升过程中始终维持球形而达到稳定的速度。工况A4、A5分布在球帽形区域。与椭球形区域相似,Mo数和Eo数较小、Re数较大时(工况A4),更难维持球形而成为球帽形,气泡最终下边界变得平坦。而A5工况Mo数和Eo数较大,下边界部分向内凹陷,上部分基本维持球形而变成椭球帽形。由此可见,三个无量纲参数Eo数、Mo数和Re数对气泡上浮形状有着密切的关系。

图5 气泡形态图谱简图以及计算结果在图谱上的分布图
2.4 球帽形区内气泡的最终速度与形状的变化关系
为了研究球帽形区域内气泡的最终形状以及速度与Mo数的关系,固定Eo数不变,对通过改变液体黏度所得的五个Mo数工况点进行计算,计算工况如表2所示。

表2 计算工况
图6则为表2中所示计算工况下气泡的最终速度和形状随Mo数变化图。上述计算条件均在球帽形区域,只改变了液体黏度的大小,Mo数中其他参数保持不变。可以看出,随着Mo数变小,气泡下表面向里凹陷的程度越大,最终难以维持基本的球形而变成球帽形。Mo数较大时,则凹陷程度越小,更接近于球形。结果表明,液体的黏度越大,Mo数越大,气泡的变形程度越小,最终速度越小。高黏度液体更有利于阻止气泡的变形和减慢运动速度。同时,据图6所得,在椭球帽区域中,气泡上浮过程中的最终速度与Mo数的对数基本成线性反比,即与黏度四次方的对数呈现反比的关系。最终速度及形状随Mo数变化图

图6 气泡最终速度与形状随Mo数变化图
3 结论
(1)经过对气泡上浮的二维数值模拟,验证了Eo数O(-1)~O(2),Mo数从O(-9)~O(4)的流动范围中,气泡最终形状包括球形、椭球形、球帽形、椭球帽形等形态。这些形状与Bhagar和Weber所得的气泡图谱相对应。
(2)三个无量纲参数Eo数、Mo数和Re数对气泡上浮形状有着密切关系。
(3)在椭球形区域内,Mo数和Eo数较小时,较难维持球形而更变得更扁。
(4)在椭球帽区域,随着Mo数变小,气泡下表面向里凹陷的程度越大,最终难以维持基本的球形而变成球帽形。
(5)高黏度液体更有利于阻止气泡的变形和减慢气泡上浮运动速度。在椭球帽区域中,气泡上浮的最终速度与Mo数的对数基本成线性反比,即与黏度四次方的对数呈反比关系。
[1]Young N O,Goldstein J S,Block M J.The Motion of Bubbles in A Vertical Temperature Gradient[J].Journal of Fluid Mechanics,1959,(3):350-356.
[2]Grace J R,Wairegi T,Nguyen T H.Shapes and Velocities of Single Drops and Bubbles Moving Freely Through Immiscible Liquids[J].Transactions of the Institution of Chemical Engineers,1976,(3):167-173.
[3]Bhaga D,Weber M E.Bubbles in Viscous Liquids:Shapes,Wakes and Velocities[J].Journal of Fluid Mechanics,1981,(105):61-85.
[4]Li Y,Yang G Q,Zhang J P,et al. Numerical Studies of Bubble Formation Dynamics in Gas-liquid-solid Fluidization at High Pressures[J].Powder Technology,2001,(2):246-260.
[5]付攀,王路.水中微气泡运动特性的理论研究与仿真[J].舰船电子工程,2009,(4):155-158.
[6]张建生,吕青,孙传东,等.高速摄影技术对水中气泡运动规律的研究[J].光子学报,2000,(10):952-955.
[7]郭容,蔡子琦,高正明.黏性流体中单气泡的运动特性[J].高校化学工程学报,2009,(6):916-921.
[8]Hirt C W,Nichols B D.Volume of Fluid(VOF)Method for the Dynamics of Free Boundaries[J].Journal of Computational Physics,1981,(1):201-225.
Numerical Simulation of Single Bubble Rising Process
ZHANG Yan1,YANG Fan1,2
(1.School of energy and power engineering, University of Shanghai for Science and Technology, Shanghai 200093; 2.Key Laboratory of multiphase flow and heat transfer of power engineering, University of Shanghai for Science and Technology,Shanghai 200093)
In order to changes in the process of understanding the bubbles form, using FLUENT software "fluid volume (volume of fluid, VOF model of a single bubble in a quiescent liquid float situation of numerical simulation by Otis number (EO) in O (- 1) -O (2), Morton number (MO) in O (- 9) to o (4) within the scope of the bubble morphology. The calculated results are compared with the bubble shape map, which verifies that the numerical values of the dimensionless parameters Eo number, Mo number and Re number are closely related to the change of the shape and the final velocity of the bubbles.
bubble floating, VOF, numerical simulation, bubble shape
上海市科学技术委员会科研计划项目(13DZ2260900)资助。

