椭球变换法建立地方独立坐标系的变形研究

尹　晖,李小祥,甘喆渊

(1.武汉大学 测绘学院，湖北 武汉 430079;2.中国电力科学研究院高压研究所,湖北 武汉 430074)



椭球变换法建立地方独立坐标系的变形研究

尹晖1,李小祥1,甘喆渊2

(1.武汉大学 测绘学院，湖北 武汉 430079;2.中国电力科学研究院高压研究所,湖北 武汉 430074)

随着我国城市基础设施建设的迅速发展，对大比例地图测绘的精度要求越来越高。而采用已有椭球参数来进行高斯平面投影却不能满足具体项目的高精度要求，必须使用新的椭球参数来建立地方独立坐标系统。一般的做法是平移中央子午线和改变投影高程面来满足城市测量中要求边长变形小于2.5 cm/km的限值。过去大部分的研究主要集中在从理论上探讨如何改变椭球参数来建立独立坐标系，缺少应用实际算例对椭球参数选择的对比和适用范围分析。本文针对3种不同方法：椭球膨胀法、椭球平移法和椭球变形法进行实例分析，选择不同椭球参数进行计算得到的新坐标系统，并进行变形分析，最后给出不同方法的优缺点及适用范围，为不同工程实践提供适宜的参考方案。

1高斯投影变形分析

由于地球是一个近似的大地椭球体，在地图投影的过程中就不可避免地产生投影变形。投影变形是指将椭球面上的元素(距离、角度、图形)投影到平面上产生的长度、角度和面积的变形。高斯投影是正形投影，角度不产生变形[1]，投影后的中央子午线是一条没有变形的直线。在中央子午线附近区域变形很小，但自中央子午线向投影带边缘，变形逐渐增加，变形最大处在投影带内赤道的两端[2]。

通常用高斯投影长度比m来表示高斯投影平面上的微分长度与地球椭球面上相应长度之比。用m-1表示投影变形的变形量大小。

设高斯平面上的某点K，用其大地坐标(B,L)和平面坐标(x,y)来表示的高斯投影长度比的计算公式[1]分别为式(1)和式(2)。

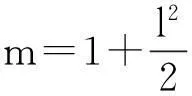
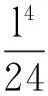
(1)

(2)

其中：u2=e′2cos2B，B,L为K点的经纬度，e′为椭球体的第二偏心率，y为K点的横坐标，R为该点处椭球的平均曲率半径，l为K点的经度差，l=L-L0，L0为选择的中央子午线经度。根据参考文献[3]可知，在l≤3.5°时，高斯投影的长度比精度优于1×10-7。表1给出了不同经差l和纬度B下的投影变形量的数值。

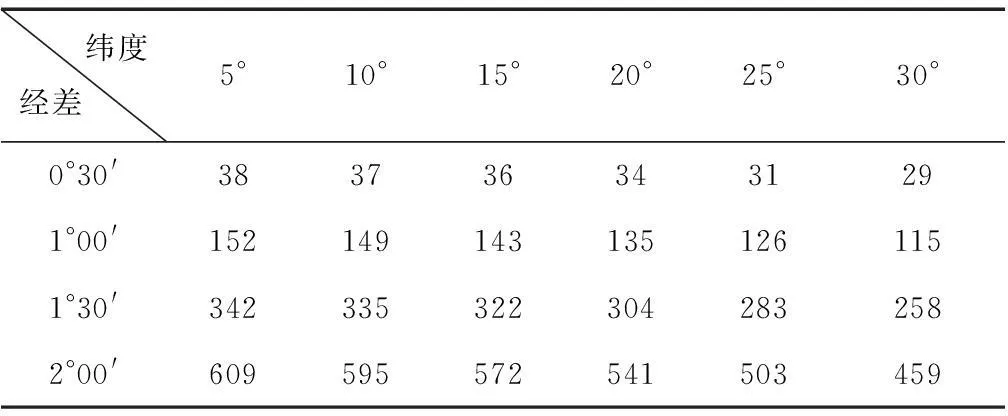
表1　不同经差l和纬度B的变形量　mm/km

从表1计算的投影变形量结果可见：由于我国地理位置位于纬度3°51′N至53°33′N的区域，在采用3°分带，最大经差1°30′的情况下，靠近投影带边缘的变形达到了200~350 mm/km，这种投影产生的长度变形远大于目前城市测量中要求长度变形小于2.5 cm/km的限值规定；从式(2)计算可以得到在横坐标y大于45 km之后，长度变形将超过1/40 000，大于工程测量中所要求的小于2.5 cm/km的长度变形误差，需要对椭球参数和投影参数进行控制。

2椭球变换法建立地方独立坐标系

2.1建立地方独立坐标系的常规方法

建立地方独立坐标系的目的就是为了控制长度变形，且保持角度不发生改变。即实际地面测得的距离转换到平面坐标系中的两者距离之差要满足实际工程的精度要求。

把地面距离观测值归算到椭球面需要归算方向(方位角)改正和距离(长度)改正。由于地面测量距离的观测值是两控制点之间的直线长度，空间直线的长度与点的铅垂线没有关系，故可以直接沿端点的法线归算致椭球面上，产生的变形为

(3)

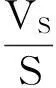
要求投影的长度变形小于等于2.5cm/km，在常规方法中只控制投影参数：改变投影面的中央子午线；改变投影面大地高；同时改变投影面的中央子午线与投影面大地高。距离控制时往往并未控制投影方向的距离改化，引起角度畸变，理论上不够严密。

对于改变投影面的中央子午线和大地高进行高斯3°带投影仍然变形超限的项目测区(如长距离道路建设、管道建设、城市级区域工程建设等)，就无法采用这种方法，需要采用椭球变换的方法建立地方独立坐标系。

2.2几种常见的椭球变换方法

2.2.1椭球膨胀法

椭球膨胀法的基本思想是保持椭球中心和椭球定向在膨胀前后不发生变动，对椭球进行缩放，缩放后的椭球面与独立坐标系所选的平面相切[4-5]。新椭球的长半轴会发生改变，椭球原点位置不发生改变(见图1)。

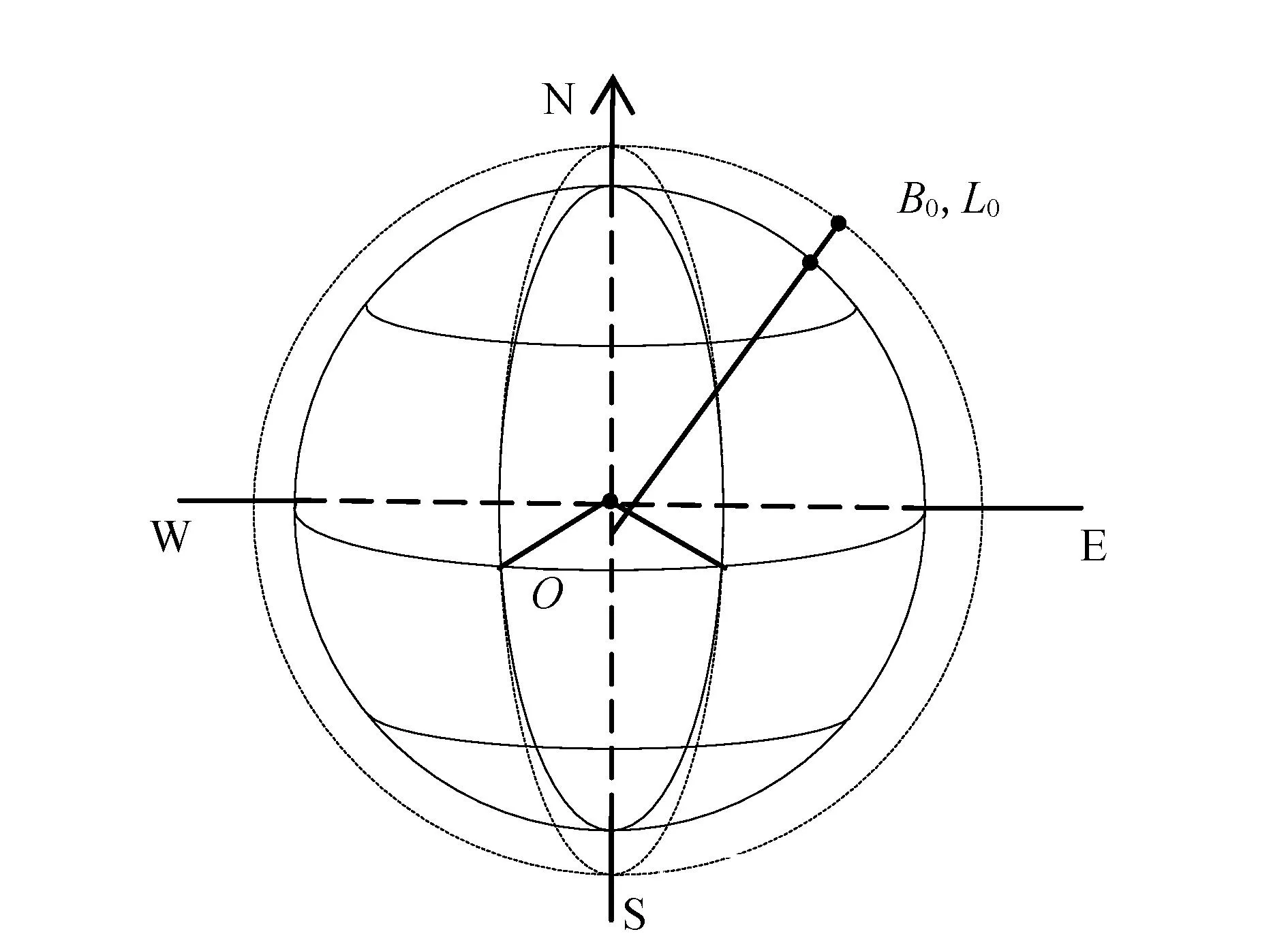
图1　椭球膨胀法变换示意图

在实际的工程使用中一般改变长半轴有3种方法，产生3种不同的结果，但都是改变椭球长半轴a而不改变椭球第一偏心率e。椭球参数变化有如下3种：

1)新椭球的长半轴增加的量为项目区域现选择的投影面大地高H。

(4)

2)新椭球的长半轴增加的量为原投影面沿法线方向膨胀到现选择的投影面的增加量。

(5)

3)新椭球的长半轴增加的量为现选择的投影面的平均曲率半径。

(6)

式中：H0为现选择的投影面的大地高，e为椭球第一偏心率(保持不变)，B0为目标区域基准纬度，L0为目标区域基准经度。

采用椭球膨胀法得到的控制点大地坐标换算到独立坐标系的计算公式为

(7)

式中：

(8)

式中：dBx,dLx,dHx为待定控制点的大地坐标变化量;Nx为待定点在原椭球参数下的子午圈曲率半径;Mx为待定点在原椭球参数下的卯酉圈曲率半径;Lx,Bx,Hx为待定控制点在原坐标系下的大地坐标。

经过椭球膨胀法的变换，待定控制点经度L不发生改变，而纬度B和大地高H发生改变。

2.2.2椭球平移法

相对于椭球膨胀法改变椭球长半轴，椭球平移法是通过移动椭球中心位置来达到效果的。其基本思想是将原椭球沿着项目区域独立坐标系的基准点所在的法线方向进行平移，使得移动后椭球面平移到现选择的投影面(见图2)。椭球的其余参数不发生改变da=0，de2=0。

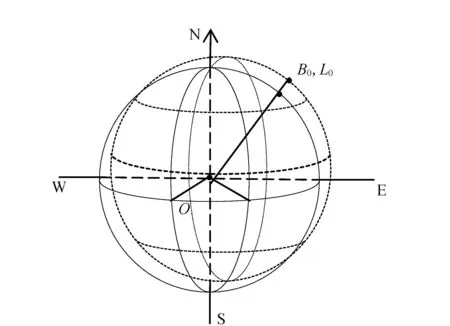
图2　椭球平移法变换示意图

椭球参数变化相应的公式为

(9)

式中：(dX0，dY0，dZ0)表示椭球中心的变化量;B0,L0,M0,N0,H0定义同椭球膨胀法。

采用椭球平移法得到的控制点大地坐标换算到独立坐标系的计算公式为

(10)

式中：dBx,dLx,dHx为待定控制点的大地坐标变化量;Mx,Nx,Hx,Lx,Bx,Hx定义同椭球膨胀法。

可见经过椭球平移法，点的经纬度和大地高都发生改变。

2.2.3椭球变形法

椭球变形的思想是保持椭球中心不发生改变，改变椭球的扁率α。具体做法是：先将椭球沿基准点的法线膨胀到所定义的参考面，变化扁率α,使得基准点处的法线方向与变换前后重合(见图3)。

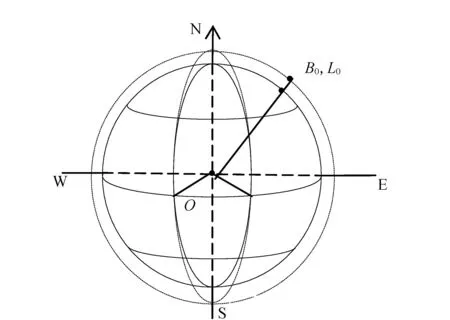
图3　椭球变形法变换示意图

这样变换的结果是保证了基准点的经度和纬度不发生改变。椭球参数相应的公式为

(11)

式中：e′2为变换后的椭球第一偏心率的平方;N0为基准点在原椭球参数下的子午圈曲率半径;da为椭球长半轴改变量;B0,N0,H0,a,e定义同椭球膨胀法。

采用椭球变形法得到的控制点大地坐标换算到独立坐标系的计算公式为

(12)

式中：dBx,dLx,dHx为待定控制点的大地坐标变化量;Mx,Nx,Hx,Lx,Bx定义同椭球膨胀法;α为原椭球扁率;dα为椭球扁率变化量;α′为新椭球扁率。

椭球平移法的变换前后可以发现待定控制点的经度L不发生改变，而纬度B和大地高H发生改变。

2.3算法流程

首先，不管采用哪种椭球变换法，需要确定目标区域基准量：基准纬度B0、基准经度L0和现选择的投影面大地高H0，B0、L0和H0可以采用项目区域已有资料中的基准点经纬度和目标投影面大地高来确定，也采用待定控制点经纬度和大地高平均值的方法计算得到。

其次是确定椭球变换参数：①椭球膨胀法是确定椭球长半轴的变化量da；②椭球平移法是确定椭球中心变化量(dX0，dY0，dZ0)；③椭球变形是确定椭球的长半轴的变化量da、新椭球偏心率e′和新椭球扁率α′。

最后是根据不同的椭球变换方法待定控制点的大地坐标改变量dBx,dLx,dHx，从而获得新椭球下的控制点大地坐标，如需要再投影成高斯平面坐标。

HDS2003和TGO是GPS数据处理的常用软件，功能强且应用面广。但这两种软件只采用了椭球膨胀法来确定椭球变换参数[6]，缺乏3种方法的效果对比。本文基于C#重新设计了建立地方独立坐标系计算软件，如图4所示。

图4　椭球变换法建立独立坐标系软件界面

3数据分析

测区为南方某市级区域，面积约1万km2，平均纬度23°30′，平均经度114°30′。现有WGS-84坐标系起算点68个。椭球变换法建立地方独立坐标系可以采用平均经纬度和大地高作为基准量，也可以采用控制点的平均经纬度和大地高作为基准量[7]。在软件设计中既设计了以区域平均经纬度和大地高作为基准量也设计了使用控制点的平均经纬度和大地高作为基准量进行计算。GPS控制点一般在山顶或者楼顶，其大地高比项目区域平均大地高偏高，故采用区域平均经纬度和大地高作为基准量，来进行数据分析[8]。

根据不同椭球变换法计算得到的椭球参数成果如表2所示。

表2　不同方法椭球参数　m

限于篇幅选择其中3个控制点(其中3号控制点为偏离中央子午线最远的点)，计算结果如表3所示(椭球膨胀法展示第一种参数下的结果)。

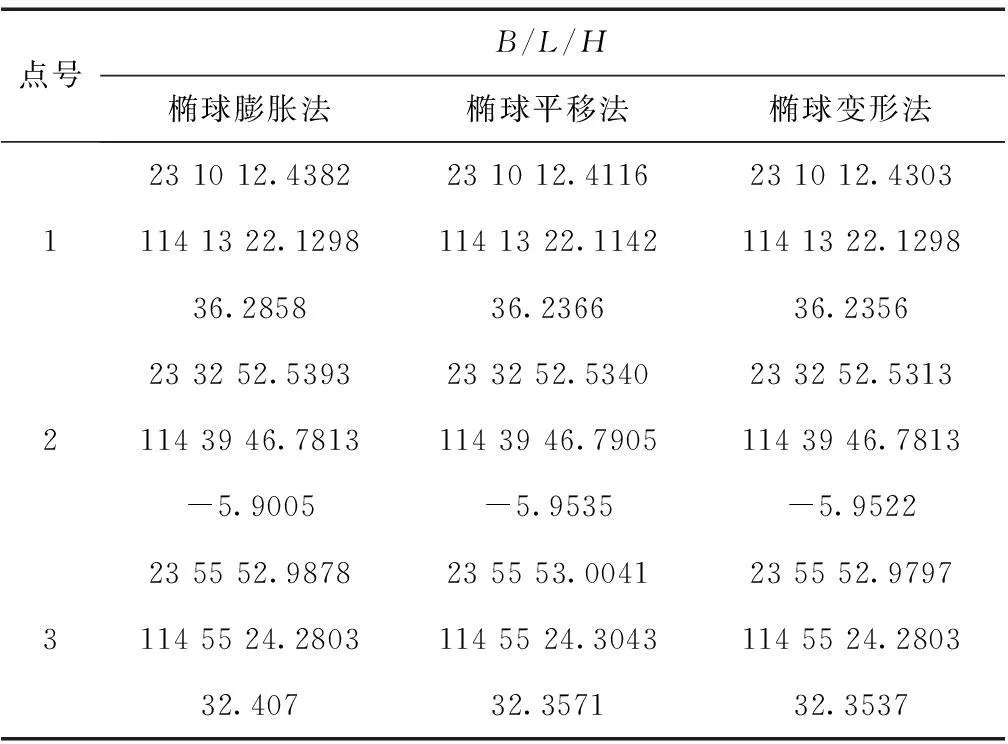
表3　不同方法计算得到的大地坐标

计算得到1、2、3号控制点和全部控制点处平均的微分长度投影变形如表4所示。

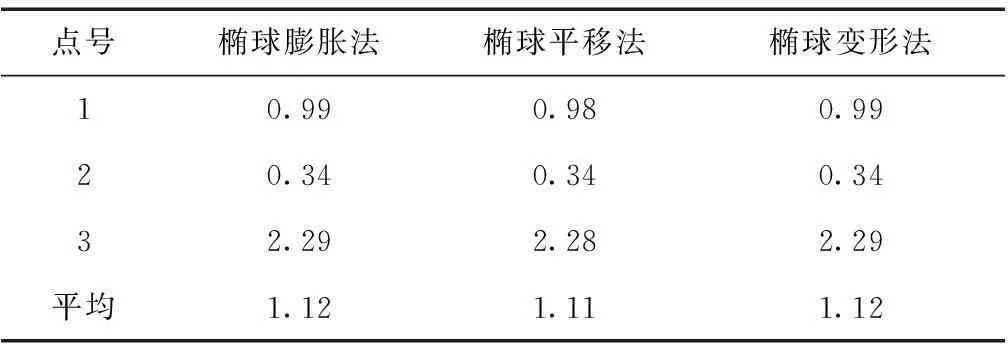
表4　3种方法每千米边长变形对比　cm/km

数据分析显示：①3种椭球变换法都对长度投影变形进行了很好的控制，满足在整个市级区域2.5 cm/km边长变形要求。椭球平移法变形较为平均，且最大变形比另外两种方法小。②在程序设计过程中因椭球平移法变换后椭球形状参数不发生改变，大地坐标投影成高斯平面坐标可以采用现有电算公式或软件，复杂性大为降低。③椭球变换法与常规方法相比，在满足城市测量2.5 cm/km的变形要求下，其控制面积达到了1万km2，大大拓展了独立坐标系的使用范围。

4结论

高斯投影变形是高斯投影的关注热点，尤其在大比例尺地形图应用中，由于精度要求较高，采用原有椭球参数进行投影就达不到实际工程的高精度要求。

1)常规方法控制投影变形控制的面积较小，计算复杂，且不具有理论严密性。椭球变换法建立独立坐标系控制面积大为增加，计算简单，具有理论严密性。

2)根据《建立相对独立的平面坐标系统管理办法》的规定：为避免重复建设，一个城市只能建立一个相对独立的平面坐标系统。因此对于基准经纬度和投影面的选择显得尤为重要。对基准的确定可以采用平均的方法，利用GPS技术快速地获取项目区域均匀分布的多个控制点，加以平均来获得基准参数，也可以根据已有资料来确定。计算得到新的椭球参数，再把新的控制点大地坐标投影到平面坐标应使用椭球变换的中央子午线，才能更好地控制投影变形。

3)在算法设计正对3种椭球变换的方法进行了程序设计。经过数据分析椭球平移法对投影变形的控制效果最好，也在算法上最简单。特别是进行高斯投影时，无需改变椭球参数，实现了快速计算。

4)根据以上分析建议使用椭球变换法中的椭球平移法来建立地方独立坐标系。

参考文献：

[1]熊介.椭球大地测量学[M].北京：解放军出版社，1988.

[2]孔祥元，郭际明，刘宗泉.大地测量学基础[M].武汉：武汉大学出版社，2010.

[3]赵俊生，刘雁春，王克平，等.关于高斯投影长度变形的探讨[J].海洋测绘，2007，27(3)：9-11.

[4]李世安，刘经南，施闯.应用GPS建立区域独立坐标系中椭球变换的研究[J].武汉大学学报(信息科学版)，2005，30(10)：888-891.

[5]魏长明，刑建国，刘小刚.利用椭球变换建立独立坐标系[J].矿山测量，2014(1)：30-32.

[6]张宏伟，康世英.基于TGO的独立坐标系与国家坐标系转换方法[J].地矿测绘，2010(2)：12-15.

[7]邱云峰，倪津，杨映泉，等.基于CGCS2000大地坐标系基准的建立与应用[J].测绘工程，2013，22(4)：42-44.

[8]张显云，杜宇，张俊.GPS技术建立地方独立坐标系的方法分析[J].矿冶工程，2012(10)：23-25.

[责任编辑：刘文霞]

摘要：在分析高斯投影变形的基础上，针对工程测量中的投影变形精度要求，阐述了3种椭球变换法建立地方独立坐标系的方法，给出具体的计算公式和参数选取原则。对3种椭球变换法进行软件设计，简化计算的工作量。并详细介绍如何求解这些参数和控制点坐标值，结合实例数据进行分析，得到不同方法建立地方独立坐标系的优缺点和适用范围。

关键词：高斯投影；椭球变换；椭球大地测量；独立坐标系

Deformation of local independent coordinate established with ellipsoid transform method YIN Hui1,LI Xiaoxiang1,GAN Zheyuan2

(1.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;2.High Voltage Department,China Electric Power Research Institute,Wuhan 430074,China)

Abstract：Based on the deformation of Gauss-Kruger projection and the requirement of projection deformation,this paper presents three different ellipsoid-transform metods to establish the independent coordinate system,specific formula and parameter selection principles.A new software is designed to avoid the shortages of current program and the calculation has been simplified.The details to solve these parameters and control point coordinates value date are analyzed with examples,and some meaningful conclusions based on different methods are drawn to show the strengths and weaknesses as well as the scope of local independent coordinate system.

Key words：Gauss-Kruger projection;ellipsoid transform;geodetic ellipsoid;independent coordinate system

作者简介：尹晖(1962-)，女，教授，博士.

基金项目：国家自然科学基金资助项目(51077105)；国家电网公司科技攻关团队资助项目(SG11013)；大地测量与地球动力学国家重点实验室开放基金资助项目(SKLGED2013-3-6-E)

收稿日期：2014-12-01

中图分类号：P226+.3

文献标识码：A

文章编号：1006-7949(2016)02-0001-05