PUMCⅡd1型青少年特发性脊柱侧凸后路三维矫形手术有限元研究

黄盛佳　霍洪军　杨学军　肖宇龙　邢文华　赵岩　祝勇　辛大齐　黄世清

010030　呼和浩特，　　内蒙古医学院第二附属医院脊柱外科(黄盛佳、霍洪军、杨学军、肖宇龙、邢文华、赵岩、祝勇、辛大齐)；510632　广州，　　暨南大学理工学院应用力学研究所(黄世清)



·临床研究·

PUMCⅡd1型青少年特发性脊柱侧凸后路三维矫形手术有限元研究

黄盛佳霍洪军杨学军肖宇龙邢文华赵岩祝勇辛大齐黄世清

010030呼和浩特，内蒙古医学院第二附属医院脊柱外科(黄盛佳、霍洪军、杨学军、肖宇龙、邢文华、赵岩、祝勇、辛大齐)；510632广州，暨南大学理工学院应用力学研究所(黄世清)

【摘要】目的建立PUMCⅡd1型青少年特发性脊柱侧凸(AIS)的三维有限元模型，模拟后路三维矫形手术操作并分析其生物力学特征。方法采集1例14岁PUMCⅡd1型AIS女性志愿者T1至骶尾骨的CT 影像图像，应用Mimics 16.0、Geomagic Studio 11.0、ANSYS 14.0软件建立完整的AIS三维有限元模型，进一步构建椎弓根钉-棒系统内固定模型并模拟后路三维矫形手术操作，记录脊柱侧凸矫正的临床指标变化，采用Von Mises应力峰值分析椎弓根钉-棒系统应力分布。结果成功建立了PUMCⅡd1型AIS三维有限元模型，模型包括523 617个单元，159 008个节点。模拟后路三维矫形手术后，AIS有限元模型的胸弯和腰弯矫形率分别达到55.7%和71.4%；顶椎区L1和L2椎体去旋转角度分别为22.77°和23.42°，其椎体质心偏移中线距离分别为6.72 mm和8.91 mm。L1椎体凸侧(左侧)螺钉应力峰值为257.82 MPa，远小于其屈服强度。顶椎区各椎体(T12～L3)凸侧螺钉应力大于凹侧，且应力集中于钉尾与钉身交界处以及钉尾与矫形棒联接处。结论AIS有限元模型的建立及手术模拟能为AIS生物力学研究提供量化指标，并为PUMCⅡd1型AIS手术方案的制定以及治疗效果的预测提供一定的理论基础。

【关键词】青少年特发性脊柱侧凸；有限元分析；生物力学；后路三维矫形

Three-dimensional finite element investigation of posterior surgical correction of PUMC type Ⅱd1 adolescent idiopathic scoliosisHUANGSheng-jia1,HUOHong-jun1,YANGXue-jun1,XIAOYu-long1,XINGWen-hua1,ZHAOYan1,ZHUYong1,XINDa-qi1,HUANGShi-qing2.

DepartmentofSpinalSurgery,theSecondAffiliatedHospitalofInnerMongliaMedicalUniversity1,Huhhot010030,China;InstituteofAppliedMechanics,CollegeofScienceandEngineeringatJinanUniversity2,Guangzhou510632,China

Correspondingauthor:HUOHong-junE-mail:huohongjun456@sina.com

【Abstract】ObjectiveTo establish three-dimensional finite element models of the Peking Union Medical College (PUMC) type Ⅱd1 adolescent idiopathic scoliosis (AIS) for simulating the posterior surgical correction and analyzing the biomechanical characteristics of pedicle screws fixation. Methods CT images were collected from a 14-year-old female volunteer. By using several kinds of software, such as Mimics 16.0, Geomagic Studio 11.0 and ANSYS 14.0, the three-dimensional finite element models of AIS was established and analyzed. The individual finite element model was applied to simulate the posterior surgical correction. The clinical indicators of AIS were recorded and the distribution of Von Mises stresses in internal fixation system was evaluated. Results The three-dimensional finite element model of PUMC type Ⅱd1 AIS was established successfully, which was consisted of 523 617 elements and 159 008 nodes. After simulation of posterior surgical correction, the correction rate of thoracic curve and main lumbar curve were 55.7% and 71.4%, respectively. Apical region L1, L2vertebra to the rotation angles were 22.77° and 23.42°, the distances from their vertebral body to the midline were 6.72 mm and 8.91 mm, and the Von Mises stress of pedicle screws of L1convex side (left side) was 257.82 MPa, far less than the yield strength. The stress of screws in the convex side was greater than the concave side, and the stress concentrated on the conjunction of rod to screw and the conjunction of nail to shank. Conclusion Three-dimensional finite element simulation is able to provide quantitative indicators of AIS biomechanics experiments, which could further establish the theoretical basis for the surgical planning and effectiveness evaluation.

【Key words】Adolescent idiopathic scoliosis； Finite element analysis； Biomechanics； Posterior three-dimensional correction

青少年特发性脊柱侧凸(AIS)指冠状面上Cobb角大于10°并伴有明显的椎体旋转和矢状面前凸或后凸异常的三维脊柱畸形。目前它的病因尚不明确，其在国内的发病率为1%～3%，但由于国内人口基数大，发病数量相当庞大[1-3]。目前矫形内固定术已成为治疗AIS的主要方法之一。近年来研究[4-5]发现，椎弓根钉-棒系统较传统的钩棒系统具有更强大的三维矫形能力。但由于AIS发病特点、发病年龄及畸形程度不同，如果手术方案设计缺乏合理性，不仅难以达到矫形的目的，而且增加了手术并发症发生率。本研究利用AIS患者的CT影像学数据，建立了T1至骶尾骨完整的AIS有限元模型，并模拟了后路椎弓根钉-棒系统内固定手术操作，通过有限元软件分析内固定物的应力分布特征，以探讨在有限元模型上模拟临床手术的可行性和治疗效果，为合理设计手术方案、评估手术效果等临床应用提供理论依据。

1 资料与方法

1.1数据及软件

选择1例女性AIS志愿者(14岁，身高142 cm，体重32.5 kg)，摄脊柱全长正侧位X线片并进行MRI扫描，排除脊柱及脊髓其他异常，结合病史确诊为AIS，进一步摄仰卧左右侧屈位(Bending位)X线片，诊断为PUMCⅡd1型[6]。在我院影像科 CT 室(扫描条件为120 KV、125 mA、层厚1.25 mm，扫描范围为T1～S1)完成CT图像数据的采集，并以标准Dicom格式进行刻盘保存。

软件：Mimics 16.0医学三维重建软件(比利时Materialise公司)；Geomagic studio 11.0逆向工程软件(美国Raindrop公司)；ANSYS 14.0有限元分析软件(美国ANSYS公司)。

1.2建立AIS三维有限元模型

将CT扫描获得的断层图像(Dicom格式)导入Mimics 16.0软件中，采用阈值分割和区域增长功能将骨组织提取出来，并对几何模型进行包裹和光顺等处理，使模型的结构外形更加逼真。运用软件的三维重建和布尔减运算生成出椎间盘(包括髓核和纤维环)、肋软骨等结构，建立包括胸廓结构的完整AIS三维几何模型(图1)，再经Geomagic Studio 11.0软件对三维模型进行光滑、打磨、去噪等图像处理，并生成三维有限元模型，最后导入ANSYS 14.0软件进一步添加韧带、设置单元类型、定义材料属性和进行有限元分析处理。

根据人体解剖学知识，通过手动在椎体前缘和后缘分别添加前纵韧带和后纵韧带，在椎板间添加黄韧带，在横突间添加横突间韧带，在棘突间添加棘间韧带和棘上韧带，在小关节之间添加关节囊韧带。韧带均采用杆单元(link 10)模拟以达到仅保持张力而无压力的特征。脊柱椎体、皮质骨、松质骨、椎间盘、肋骨、肋软骨和胸骨等均采用solid 187四面体单元，而韧带均采用link 10杆单元。将关节突关节定义为面-面接触，由于关节被关节囊韧带包裹且关节面之间的摩擦很小，因此将模型中小关节的面-面接触定义为无摩擦特性。

骨性结构和椎间盘均模拟为各向同性的弹性材料。根据文献[7-10]确定骨、椎间盘、软骨、韧带属性(下页表1)。将各个结构材料的弹性模量、泊松比和横截面积等材料系数输入模型中，最终在ANSYS 14.0软件内建立完整的PUMCⅡd1型AIS三维有限元模型(图2)。

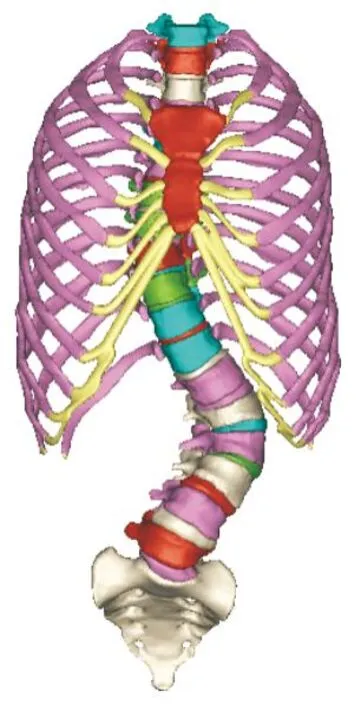
图1　完整的AIS三维几何模型

图2　完整的AIS三维有限元网格

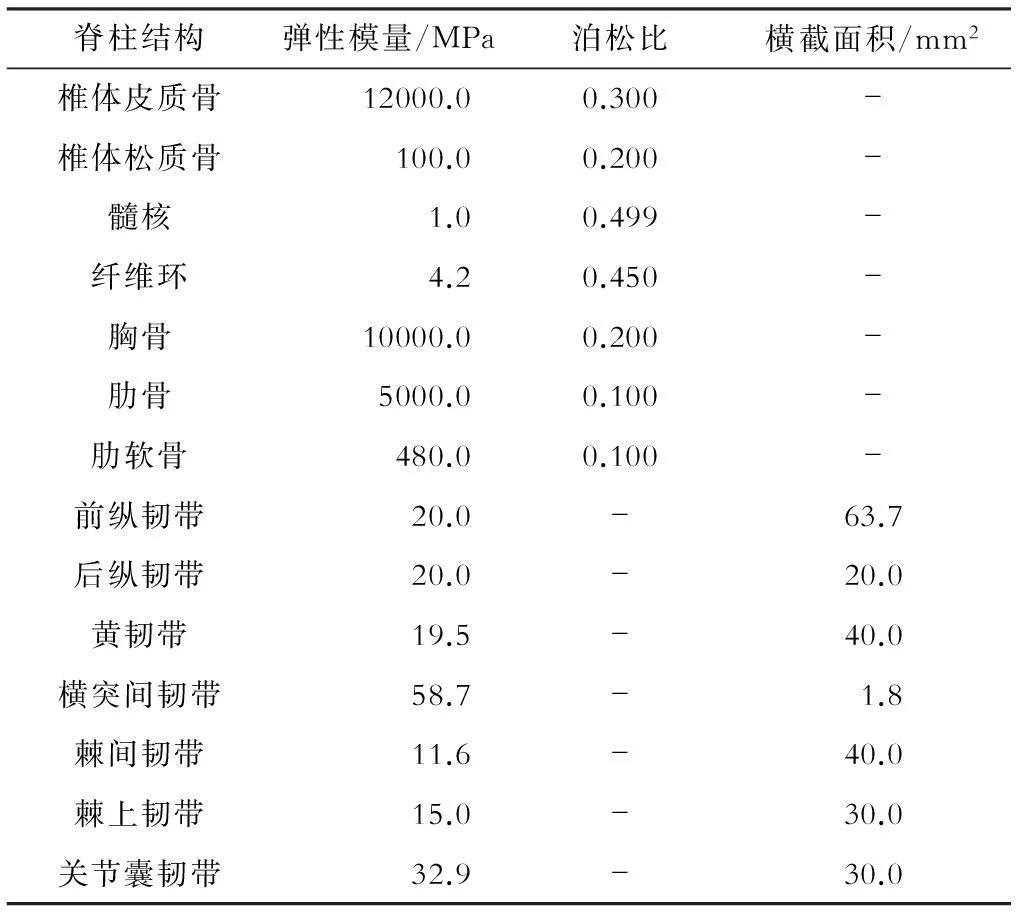
脊柱结构弹性模量/MPa泊松比横截面积/mm2椎体皮质骨12000.00.300-椎体松质骨100.00.200-髓核1.00.499-纤维环4.20.450-胸骨10000.00.200-肋骨5000.00.100-肋软骨480.00.100-前纵韧带20.0-63.7后纵韧带20.0-20.0黄韧带19.5-40.0横突间韧带58.7-1.8棘间韧带11.6-40.0棘上韧带15.0-30.0关节囊韧带32.9-30.0

1.3验证AIS三维有限元模型有效性

本研究通过从测算模型中提取2个相对正常的节段(T1～4和L5～S1)，将其在各种工况加载下的活动度与Busscher等[11]、Yamamoto等[12]实验结果进行比较，来验证该模型的有效性。有限元模型的边界状态和载荷设定：T1～4节段为完全约束T4椎体下表面，在T1的上表面分别加载大小均为4 Nm的力矩来模拟屈伸、左右侧屈和轴向旋转运动；L5～S1节段为完全约束骶尾骨的表面，在L5的上表面分别加载大小均为10 Nm的力矩来模拟屈伸、左右侧屈和轴向旋转运动。随后进行有限元运算分析，在ANSYS软件后处理中获得2个节段模型的活动度。

1.4建立椎弓根钉-棒内固定有限元模型

预先在ANSYS软件中建立椎弓根钉-棒内固定系统的有限元模型(图3)。模型均采用四面体实体单元，脊柱与螺钉之间的交界面采用理想黏接，限制椎体螺钉界面间所有方向的自由度，钉-棒之间则定义为面-面接触，限制螺钉与螺帽界面之间所有方向的自由度。将矫形的棒轴心位置与螺钉中心连接成圆柱关节，只允许上下位移和左右旋转，模拟手术矫形过程中螺钉沿棒上下滑动及自由旋转，而将上下固定椎的螺钉与矫形棒设置为单纯的旋转自由度。内固定物的材料均为钛合金，其弹性模量和泊松比分别为110 GPa和0.3。

1.5后路三维矫形手术操作的有限元模拟

由于本研究AIS为PUMCⅡd1型，根据邱贵兴等[6,13]的报道对该类AIS可采用单纯固定融合主腰弯畸形。本研究的手术方案设计采用T10～L5全节段椎弓根螺钉内固定的方法。于术前模拟后路广泛松解操作，即去除融合节段内所有的黄韧带、棘突上韧带、棘突间韧带和关节囊韧带等结构。在模拟手术操作过程中，先在侧凸融合范围内(T10～L5)双侧置入椎弓根螺钉，将矫形棒预弯成矢状面腰椎的生理曲度，在腰弯凸侧(左侧)置入第1个矫形棒，并逐节段完成钉棒链接操作，此过程中需适度压棒，以减少冠状面的侧凸，同时加大腰椎生理前凸；将矫形棒转动90°后，使得冠状面上侧凸畸形转变成矢状面上腰椎生理前凸。在腰弯凹侧(右侧)置入另一矫形棒并半锁紧螺钉，可根据患者实际情况在凸侧螺钉间适当加压而在凹侧适当撑开，目的是为了增大矢状面上腰椎前凸曲度，最后待矫形满意后即可锁紧全部螺钉(图3)。

1.6评估指标

记录冠状面 Cobb 角、矢状面前凸角、顶椎区各椎体旋转情况和位移及椎弓根螺钉的应力分布情况。

图3后路矫形过程模拟图(后面观)a. 置入椎弓根螺钉 b. 置入矫形棒c. 90°转棒d. 置入稳定棒并锁定

2 结果

2.1AIS三维有限元模型的建立

完整建立了PUMCⅡd1型AIS三维有限元模型，包括胸腰椎、骶尾骨、胸廓、椎间盘及脊柱所有韧带等结构。共包括522 887个四面体单元和730个杆单元，共计523 617个单元、159 008个节点，其中采用14种材料性质、2种单元类型。所建立的AIS三维有限元模型外形逼真，几何相似性较高。

2.2AIS三维有限元模型的有效性验证

将提取的T1～4和L5～S1模型在屈伸、侧屈和旋转模拟状态下的活动度分别与 Busscher等[11]和Yamamoto等[12]的实验结果相比较，其结果吻合度较好(图4、5)，因此可认为本模型符合AIS患者个性化生物力学特征，能用于下一步实验研究。

图4T1～4节段模型活动度与Busscher等的实验结果比较

图5L5～S1节段模型活动度与Yamamoto等的实验结果比较

2.3矫形效果及临床相关指标

完成三维有限元模型矫形加载模拟后，其最终的矫形效果和位移云图见图6。本研究中术后胸弯矫形率为55.7%，腰弯矫形率为71.4%，腰椎前凸角增大，均较术前明显改善(表2)；脊柱侧凸冠状面Cobb角明显改善，矢状面腰椎前凸的正常生理曲度得以维持。

表2　手术前后脊柱冠状面和矢状面

通过模拟手术发现，后路椎弓根钉-棒系统内固定能很好地消除顶椎区域各椎体旋转，具有良好的去旋转及强大的中线纠正能力(表3)。

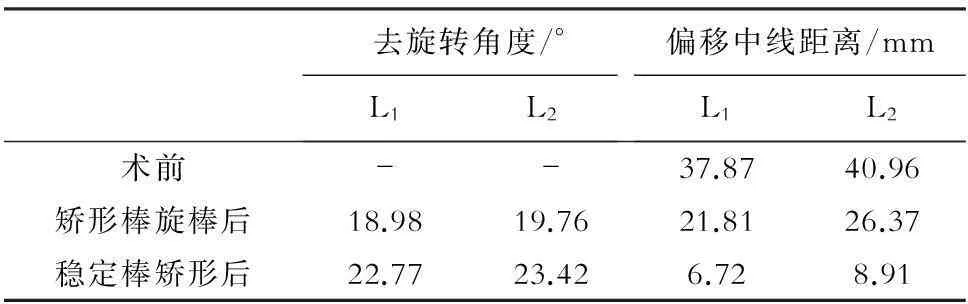
表3　手术前后顶椎区各椎体去旋转

2.4椎弓根螺钉应力分布变化

术后各椎弓根螺钉最终应力分布情况见图7，结果显示L1椎体凸侧(左侧)螺钉的最大应力值达257.82 MPa，远小于其屈服强度[14]，且椎弓根螺钉应力高值主要集中在顶椎周围节段，其中顶椎区域各椎体(T12～L3)的凸侧螺钉应力大于凹侧，且应力主要集中在钉尾与钉身交界处及钉尾与矫形棒联接处(图8)。

图6　术后脊柱最终位移云图(mm)

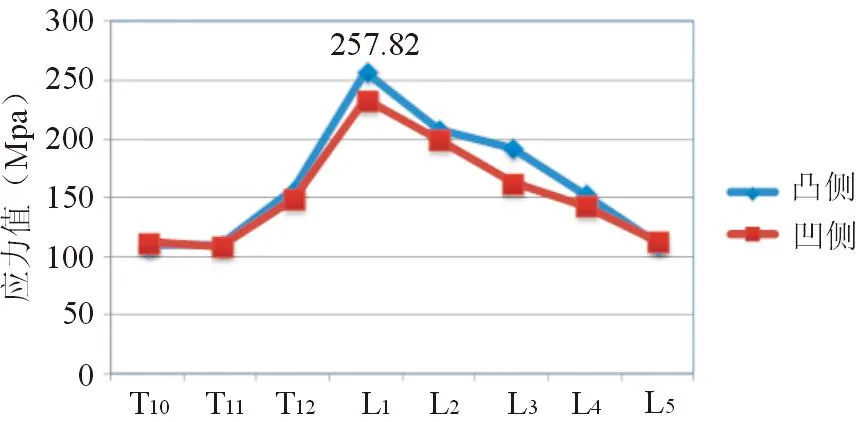
图7　术后各螺钉应力值折线图

图8　术后螺钉应力分布图(MPa)

3讨论

3.1AIS有限元分析

AIS对患者的外观、生活质量和心肺功能等造成了极大的危害，目前临床上矫形内固定手术已成为治疗AIS的主要方法，但其操作复杂，风险较大,且手术方案的制定往往是根据术者的临床经验，缺乏不同患者、不同畸形类型的生物力学研究依据。由于难以建立有意义的动物模型和获得尸体标本[15-16]，传统生物力学实验研究远远不能满足AIS生物力学实验的需要。有限元分析是一种新型计算机模拟生物力学实验的方法，它是对传统生物力学机制研究的有效补充和创新。

AIS畸形结构复杂，建模较为困难，且其模型缺少有效的体外实验数据验证，故有限元方法运用于AIS的研究相对较晚。Viviani等[17]于1986年最早将有限元方法应用在脊柱侧凸手术模拟领域，但由于采用的是简易的线性二维模型，难以真实反映脊柱侧凸患者的情况。Lafage等[18]于2004年首先对所建立的脊柱侧凸患者三维有限元模型进行CD矫形手术的模拟，经置入钉-棒、90°转棒及置入稳定棒和锁定，最后释放应力。Little等[19]在建立的8例AIS有限元模型上模拟矫形手术，发现术后位于或邻近顶椎的椎间盘所受应力最大，脊柱侧凸畸形大多数发生在顶椎相邻椎体，且AIS冠状面矫形效果主要影响因素是椎间盘空间。Pasha等[20]建立了11例右主胸弯、23例左胸腰弯的脊柱侧凸患者及12例正常人的个体化有限元模型，发现脊柱侧凸组与对照组骶骨上终板应力分布重心位置显著不同，在脊柱和骨盆之间传递负荷时，胸腰弯患者对骶骨负荷影响较主胸弯患者大。Abe等[21]在矫形术前后对20例AIS患者进行CT扫描及有限元分析，证实术中凹侧矫正力较凸侧大4倍左右，其中螺钉拔出力和推进力均明显低于之前文献的安全值。目前采用CT或MRI影像学数据建立个体化脊柱侧凸模型并对有限元模型进行手术模拟已成为有限元研究的新方向，应用逆向工程软件及有限元分析软件对所建立的模型进行有限元分析研究不仅能准确地模拟手术矫形过程，还能为手术方案设计和术后效果预测提供理论依据。

3.2本研究有限元模型的特点

本研究是利用螺旋CT连续扫描图像而构建的模型，包含了胸廓结构以及从T1至骶尾骨所有的脊柱结构。对于CT图像上难以显示的椎间盘和肋软骨，本研究根据其解剖位置关系通过Mimics软件来重建，并将椎间盘进一步划分了纤维环和髓核两部分。此外，根据解剖定位添加了黄韧带、前纵韧带、后纵韧带、横突间韧带、棘间韧带、棘上韧带和关节囊韧带等，使得所建的模型更接近患者真实效果，也更符合个体化生物力学研究的要求。因此，所建立的模型不仅几何形态相似度较高，还能准确地分析脊柱和相关结构的生物力学特点。该有限元模型主要包括14种材料性质和2种单元类型，还包括730个link 10杆单元和522 887个solid 187四面体实体单元，共计523 617个单元。与其他研究建立的模型相比，本研究所建的AIS模型具有简化程度较低、精确度及几何相似性较高的特点，因此其符合后续的生物力学实验研究的要求。

本研究采用医学三维重建软件Mimics和逆向工程软件Geomagic studio，并导入有限元分析软件ANSYS进行添加韧带、设置单元类型和赋予材料属性，建成了高质量的PUMCⅡd1型AIS三维有限元模型，再提取所建模型的2个相对正常节段(T1～4和L5～S1)分别与Busscher等[11]和Yamamoto等[12]的实验数据进行验证，结果显示两者吻合度较好，证实该模型可靠性和有效性较好，能较客观地体现PUMCⅡd1型AIS患者个性化生物力学属性，为该类型患者生物力学研究和手术分析、设计提供可靠的数字化平台。

3.3本研究有限元模拟结果的分析

本研究参考邱贵兴等[6]关于特发性脊柱侧凸PUMC分型系统的手术推荐方案，对PUMCⅡd1型AIS有限元模型进行后路手术矫形模拟，并获得了令人满意效果。本研究通过模拟后路椎弓根钉-棒系统内固定来矫正脊柱侧凸畸形，手术矫形后主腰弯的Cobb角度从术前55.4°矫正为15.8°，其矫形率达到71.4%；代偿性胸弯的Cobb角度从术前35.0°自发矫正为15.5°，其矫形率达到55.7%。手术矫形模拟结果显示，在顶椎区各椎体(T12～L3)的螺钉应力值较高，其中L1椎体凸侧螺钉最大应力值达257.82 MPa，参考钛合金螺钉屈服强度为894～2 068 MPa[14]，本研究模拟的手术方法中各螺钉应力值均远远低于其屈服强度，提示术中和术后内固定物疲劳或断裂的可能性较低。同时，该患者主腰弯椎体和内固定物对应的Von Mises应力峰值较胸弯椎体高，尤其是L1和L2的应力达到最高值，表明主腰弯顶椎区椎体的畸形程度较严重，术中椎体的去旋转角度较大，且向中线纠正距离较长，使得应力多集中在主腰弯顶椎区各椎体和内固定物上。因此，笔者建议在对该类患者实施后路三维矫形手术时，应在顶椎区各椎体上置入椎弓根螺钉(双侧置钉)，并尽可能选用直径、长度与术前测量数据最接近的螺钉，目的是避免顶椎区椎体承受应力过度集中导致椎体骨折或钉道切割现象，以及避免螺钉松动或断裂现象，以保证后路矫形手术的安全性和有效性。

通过有限元模拟手术的数据分析可了解AIS患者术后Von Mises应力分布情况，这不仅可明确后路矫形手术多个节段螺钉的应力分布规律，还能判断螺钉与骨质之间以及螺钉与矫形棒之间的应力变化。本研究通过对所建模型进行后路三维矫形手术操作的模拟，在矫形完成后脊柱侧凸椎体序列和生物力学特征均发生明显改变。术后顶椎区各椎体(T12～L3)的螺钉应力峰值均较高，其中凸侧椎弓根螺钉应力值均明显高于凹侧。因此，临床制定脊柱侧凸手术方案时，应保证该区域凸侧椎弓根螺钉的数量，并尽可能地选用规格合适的椎弓根螺钉。此外，术后内固定物的应力分布主要集中在钉尾与钉身交界处及钉尾与矫形棒联接处。有限元模拟研究能进一步发现应力遮挡和应力过于集中部位的分布规律，以提示及时调整和更换内固定物，防止出现严重的钉棒变形或断裂。因此，对AIS患者术后生物力进行分析研究，可大大提高内固定物使用的安全性和有效性，也能为AIS手术治疗方案的制定提供一定的理论支持。

3.4不足之处

本研究尚存在不足之处：三维有限元模型的材料属性数据均来自于国内外相关文献报道，且缺乏同类实验结果的参照对比；在建模过程中对有限元模拟进行了一定的线性简化处理；在模拟手术过程中无法保持序贯的手术操作，故只能分析比较手术矫形的始末状态，使得有限元模拟研究与实际的生物力学实验存在一定差异；由于AIS是一极其复杂的整体，涉及到肌肉和韧带的牵拉作用、脊髓神经的耐受能力以及强大的代偿能力等问题，计算机模拟难以达到真实的临床手术操作。因此，有限元模拟研究结果只能提供参考和方向性的指导作用，并不能完全取代传统生物力学实验。但随着有限元建模技术和有限元分析方法的不断改良，这些问题有望得到进一步解决。

综上所述，本研究在PUMCⅡd1型AIS有限元模型上进行了后路三维矫形手术的有限元模拟，探索出一套具有通用性脊柱侧凸手术矫形的有限元模拟方法，搭建了具有个体化生物力学特性的脊柱侧凸数字化平台，为进一步预测患者治疗效果、制定手术矫形策略以及探讨脊柱侧凸治疗中的争议等提供了参考依据。

参考文献

[1]李明,侯铁胜. 脊柱侧凸三维矫形理论与技术[M]. 上海: 第二军医大学出版社，2001:2.

[2]江汉,江毅,赵春风,等. 天津市红桥区57所小学在校学生脊柱侧弯患病率的调查[J]. 中华骨科杂志, 1994, 14(6):362-364.

[3]Lonstein JE. Scoliosis: surgical versus nonsurgical treatment[J]. Clin Orthop Relat Res, 2006, 443:248-259.

[4]Halm H, Niemeyer T, Link T, et al. Segmental pedicle screw instrumentation in idiopathic thoracolumbar and lumbar scoliosis[J]. Eur Spine J, 2000, 9(3):191-197.

[5]Wang Y, Fei Q, Qiu G, et al. Anterior spinal fusion versus posterior spinal fusion for moderate lumbar/thoracolumbar adolescent idiopathic scoliosis: a prospective study[J]. Spine (Phila Pa 1976), 2008, 33(20):2166-2172.

[6]Qiu G, Zhang J, Wang Y, et al. A new operative classification of idiopathic scoliosis: a peking union medical college method[J]. Spine (Phila Pa 1976), 2005, 30(12):1419-1426.

[7]Goel VK, Monroe BT, Gilbertson LG, et al. Interlaminar shear stresses and laminae separation in a disc. Finite element analysis of the L3-L4 motion segment subjected to axial compressive loads[J]. Spine (Phila Pa 1976), 1995, 20(6):689-698.

[8]Nie WZ, Ye M, Liu ZD, et al. The patient-specific brace design and biomechanical analysis of adolescent idiopathic scoliosis[J]. J Biomech Eng, 2009, 131(4):041007.

[9]Kim HJ, Chun HJ, Kang KT, et al. A validated finite element analysis of nerve root stress in degenerative lumbar scoliosis[J]. Med Biol Eng Comput, 2009, 47(6):599-605.

[10]Chen CS, Cheng CK, Liu CL, et al. Stress analysis of the disc adjacent to interbody fusion in lumbar spine[J]. Med Eng Phys, 2001, 23(7):483-491.

[11]Busscher I, van Dieen JH, Kingma I, et al. Biomechanical characteristics of different regions of the human spine: an in vitro study on multilevel spinal segments[J]. Spine (Phila Pa 1976), 2009, 34(26):2858-2864.

[12]Yamamoto I, Panjabi MM, Crisco T, et al. Three-dimensional movements of the whole lumbar spine and lumbosacral joint[J]. Spine (Phila Pa 1976), 1989, 14(11):1256-1260.

[13]邢泽军,仉建国,邱贵兴,等. 全节段椎弓根螺钉后路选择性融合胸弯或腰弯后代偿弯的自发性矫形比较[J]. 中华骨科杂志, 2010, 30(5):461-467.

[14]邹德威,杨惠林,金大地,等. 脊柱功能重建外科学: 高级理论和技巧[M]. 北京: 人民军医出版社, 2008:65-66.

[15]Shono Y, Kaneda K, Yamamoto I. A biomechanical analysis of Zielke, Kaneda, and Cotrel-Dubousset instrumentations in thoracolumbar scoliosis. A calf spine model[J]. Spine (Phila Pa 1976), 1991, 16(11):1305-1311.

[16]Braun JT, Ogilvie JW, Akyuz E, et al. Creation of an experimental idiopathic-type scoliosis in an immature goat model using a flexible posterior asymmetric tether[J]. Spine (Phila Pa 1976), 2006, 31(13):1410-1414.

[17]Viviani GR, Ghista DN, Lozada PJ, et al. Biomechanical analysis and simulation of scoliosis surgical correction[J]. Clin Orthop Relat Res, 1986, 208:40-47.

[18]Lafage V, Dubousset J, Lavaste F, et al. 3D finite element simulation of Cotrel-Dubousset correction[J]. Comput Aided Surg, 2004, 9(1-2):17-25.

[19]Little JP, Izatt MT, Labrom RD, et al. An FE investigation simulating intra-operative corrective forces applied to correct scoliosis deformity[J]. Scoliosis, 2013, 8(1):9.

[20]Pasha S, Aubin C, Parent S, et al. Biomechanical loading of the sacrum in adolescent idiopathic scoliosis[J]. Clin Biomech (Bristol, Avon), 2014, 29(3):296-303.

[21]Abe Y, Ito M, Abumi K, et al. Scoliosis corrective force estimation from the implanted rod deformation using 3D-FEM analysis[J]. Scoliosis, 2015, 10(Suppl 2):S2.

(收稿：2015-05-03; 修回：2015-10-26)

(本文编辑：卢千语)

DOI：10.3969/j.issn.1673-7083.2016.01.011

通信作者：霍洪军E-mail: huohongjun456@sina.com

基金项目：国家自然科学基金(81160216)