复合相变材料导热系数的分形研究

余杨敏，李 彦，朱群志，李 鹏（上海电力学院，上海 200090）

复合相变材料导热系数的分形研究

余杨敏，李 彦，朱群志，李 鹏
（上海电力学院，上海 200090）

导热系数是复合相变材料一个重要的物性参数，常温下的热导采用实验的方法测量，得到的数据较为准确。分形理论通过分形体的自相似原则，来达到简化复合材料微观结构的目的。在之前的研究基础上结合制备出的LiNO3-KNO3/EG相变材料计算其有效导热系数，并与实验数据进行对比。

复合相变材料；有效导热系数；分形理论

无机盐作为相变材料的一种具有储能密度大、传热性能好以及成本低等优点，由于无机盐相变材料导热系数低，限制了其应用。通过添加高导热材料来提高相变材料的导热系数，可明显增大其导热系数。Ma等[1]采用 Sierpinski地毯结构建立了一个空气-水-固体颗粒三组分非饱和土壤系统的导热模型。黄昭雯[2]首次将分形理论应用于熔盐/膨胀石墨复合材料中，提出了新的模型计算熔盐复合材料的导热系数。本文在已有的研究基础上，结合制备出的LiNO3-KNO3/EG复合材料计算其导热系数，并与所测得的实验数据进行对比研究。

1 分形模型的建立

LiNO3-KNO3/EG复合材料由熔盐晶体、石墨片层以及孔隙三部分组成，故可看成LiNO3-KNO3/EG应为两相的多孔体系，即认为将孔隙和石墨片层合并为多孔EG基质。根据Yu 等[1，3]对复杂多孔介质体系的分形研究结果，公式（1）给出了复合材料中自相似区域的度量尺度区间、分形维度Df和材料中多孔EG 基质的体积分数三者之间的关系。

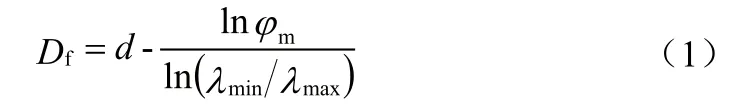
其中，d表示欧几里德维度。选取d=2二维平面的情况。

复合材料的表观密度为750～1450 kg/m3，EG的质量分数为5%～30 %时，多孔EG基质的体积分数在0.30～0.70范围内。公式（2）来计算不同单元的分形维度，划分相应的。

由公式（1）和公式（2）中Df和EG的体积分数及参数i、j的关系可以求出不同EG基质所对应的分形维度。当i=4时，不同的分形单元对应的j不相同，单元A、B、C、D对应的j分别为1，2，3，4。

2 复合材料导热系数的计算

热量从分形单元的上部进入，简化为一维导热模型。分形单元有效导热系数与其内部结构之间的关系可以通过采用一维导热假设同时类比电导率计算的方式建立。

A型单元导热系数的计算

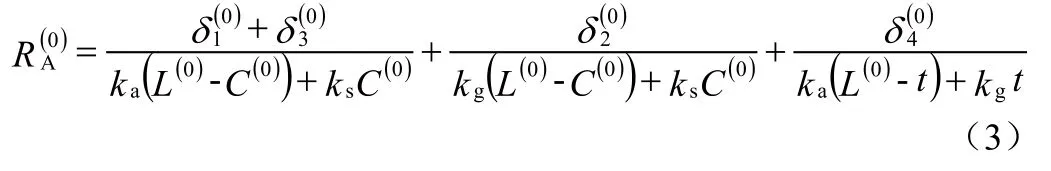
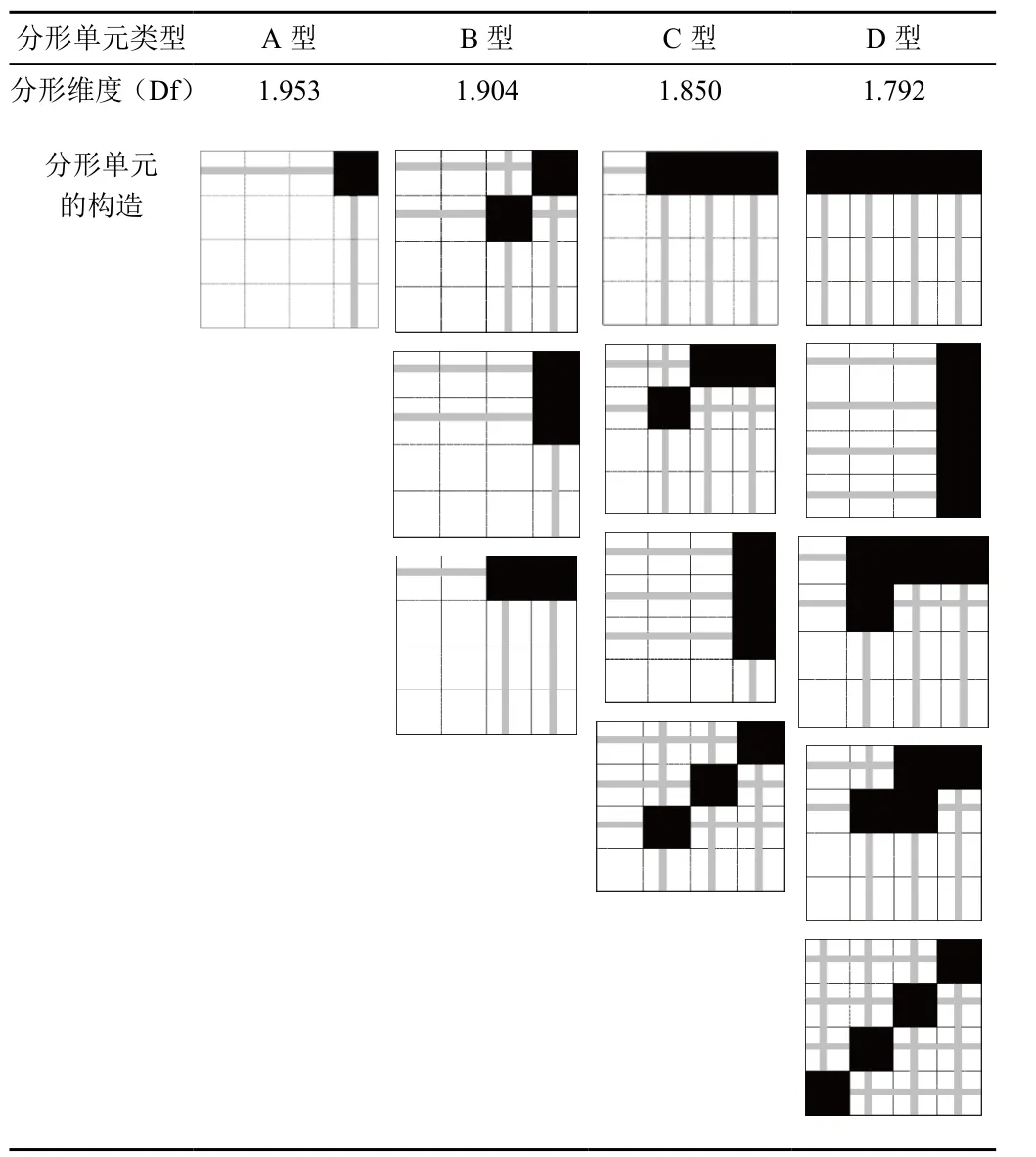
表1 分形单元

再根据傅里叶定律可知，在一维导热的情况下，其导热系数和热阻有如下关系：

一级结构的有效导热系数的计算也采用类似的方法。由于Serpinski地毯的零级结构是一级结构的组成部分，因此可以将零级结构看成是导热系数为的匀质材料，并用其代替下一级结构中表示孔隙的区域。迭代可得出一级A型分形单元的有效导热系数，表达式如公式（5）所示：

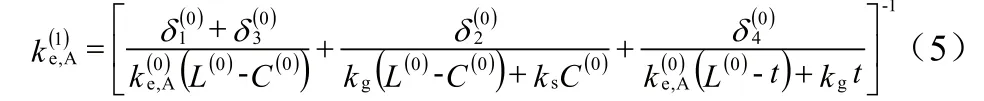
同理可得到n级A型分形单元的有效导热系数：

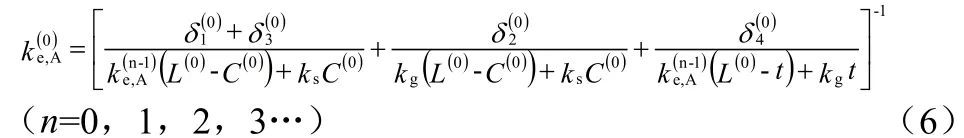
则式（6）所得出的就是A型单元最后的有效导热系数表

B、C、D型单元导热系数的计算

同理可求得B、C型和D型各个构造的零级导热系数，采用与上述相同的迭代方式，可以得到B、C型和D型单元的有效导热系数、和。

依照Ma[1]及Pia[3]等研究者使用的方法，即认为选用的两个不同类型的分形结构单元沿着热流方向并联连接，则复合材料的总的有效导热系数的可按照下式计算：

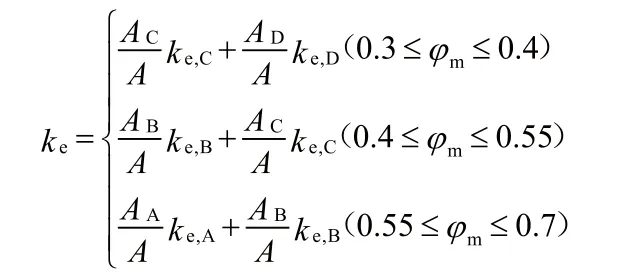
3 复合相变材料导热系数的实验测定

未添加EG的混合熔盐的平均导热系数仅为1.16W/（mK），EG含量为5%、10%、15%、20%以及30%的复合材料的平均导热系数分别为5.08W/（mK）、9.13W/（mK）、11.97W/（mK）、15.03W/（mK）、16.17W/（mK）。

4 结论

通过分形理论计算出的复合材料导热系数与实验数据进行对比。可以得出结果，复合相变材料的实验值与预测值的误差分别为10%、6.21%、3.55%、1.19%、7.14%，平均误差在10%左右。说明该导热模型在LiNO3-KNO3/EG复合材料中计算其有效导热系数较为正确。

[1] Ma，Y.，Yu，B.，Zhang，D.，et al.Fractal geometry model for effective thermal condicity of three-phase porous media[J].Journal of Applied Physics，2004，95（11）；6426-6434.

[2] Zhaowen Huang，Dehuai Zhai，Xuenong Gao，Tao Xu，Yutang Fang，Zhengguo Zhang.Theoretical study on effective thermal conductivity of salt/expanded graphite composite material by using fractal method[J].Applied Thermal Engineering，2015，86：309-317.

[3] Pia，G.，Sanna，U.Intermingled fractal units model and electrical equivalence fractal approach for prediction of thermal conductivity of porous materials[J].Applied Thermal Engineering，2013，61（2）：186-192.

Fractal Study on Thermal Conductivity of Composite Phase Change Materials

Yu Yang-min，Li Yan，Zhu Qun-zhi，Li Peng，

Thermal conductivity is an important physical property parameter of composite phase change material.The thermal conductivity at room temperature is measured by experimental method.Fractal theory is used to simplify the microstructure of composite materials by the principle of self similarity.On the basis of previous studies，the effective thermal conductivity of LiNO3-KNO3/EG phase change material was calculated and compared with the experimental data.

composite phase change material；effective thermal conductivity；fractal theory

TB34

A< class="emphasis_bold">文章编号：1

1003-6490（2016）12-0051-02

2016-12-17

余杨敏（1991—），女，江西鹰潭人，研究生，主要研究方向为相变储能材料以及热物性。达式，记为。