先简支后连续T梁桥全过程力学行为及极限承载力分析



先简支后连续T梁桥全过程力学行为及极限承载力分析

朱小青，陈代海，陈淮

(郑州大学 土木工程学院，河南 郑州 450001)

先简支后连续T梁桥是国内外高速公路在用的一种桥梁结构新形式，具有施工较简易、行车条件较好且经济合理，兼备简支梁与连续梁桥的优点，因而在桥梁工程中得到了越来越多的应用[1-2]。目前，对该类型的桥梁进行试验无疑是研究其极限承载力最直接有效的方法，但也存在着诸如成本较高、费工费时等缺点，尤其对于新建桥梁，不可能为研究极限承载力而进行破坏试验，作为一种经济、省时且行之有效的方法，数值仿真分析弥补了上述缺点[3]。然而，由于有限元分析中涉及到材料和几何双重非线性，计算工作量很大，且收敛困难；此外，桥梁结构的极限承载力受施工工艺和施工过程的影响很大[4-5]，目前关于先简支后连续T梁桥结构从施工至加载到承载能力极限状态的全过程分析并不多见。为此，本文以河南省省道S318线西张村大桥为工程背景，运用有限元软件Midas/FEA建立了该桥的实体模型，模型考虑了几何非线性和材料非线性，同时运用软件提供的单元激活与钝化功能，分别在6种工况下对先简支后连续T梁桥结构从施工至极限破坏的受力全过程进行了模拟，根据计算得到的破坏荷载、破坏特征、荷载位移曲线以及桥梁安全系数等，评定了该桥的极限承载力。

1工程概况

西张村大桥是河南省省道S318线上一座重要的高墩桥梁，该桥桥面净宽12 m，双向两车道设计，横向由5片T梁组成，采用先简支后连续梁桥体系，共3联11孔。其中第一联由4×50 m的预应力混凝土连续T梁横向组合连接构成，总长200 m，如图1所示。

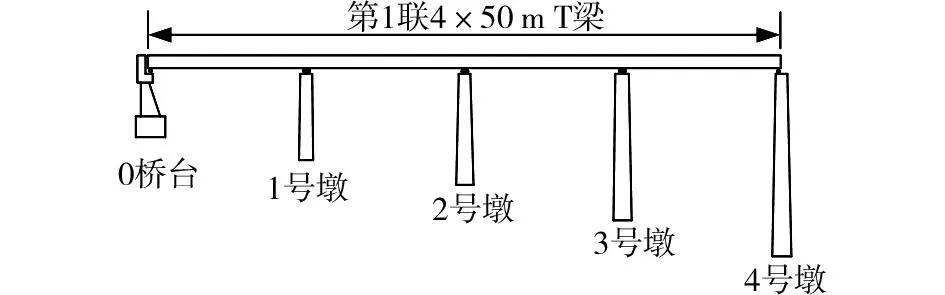
图1　西张村大桥立面示意图Fig.1 Facade schematic of Xizhangcun bridge

以桥梁上部结构先简支后连续预应力混凝土T梁为研究对象，其详细的设计参数如下。

设计荷载：公路—I级。

主梁：每片T梁高2.7 m，宽2.4 m，边梁预制宽度为1.95 m，中梁预制宽度为1.5 m；主梁梁肋厚度支点处为0.6 m，跨中处为0.2 m(见图2)，在支点附近4.8m范围内逐渐加宽，在支点位置梁肋加宽至马蹄宽。

横隔板：全梁共设7道横隔板，其中端横梁2道，为实体矩形截面，中横梁5道，横隔梁间距为8.1 m；

单位：cm图2　主梁跨中横断面图Fig.2 Section views of girder span

桥面现浇层：成桥后采用10 cm混凝土现浇面层+9 cm厚沥青混凝土，模型计算时考虑4 cm的混凝土现浇层参与受力；

主梁、湿接缝及桥面现浇层混凝土的强度等级：C55；

预应力钢绞线为低松弛高强度预应力钢绞线，单根钢绞线直径为15.2 mm，公称面积为140 mm2，标准强度为1 860 MPa，控制张拉力为标准强度的70%，采用应力、应变双控制，后张法施工，此外，管道摩擦因数为0.25，管道偏差因数为0.001 5 m-1；

普通钢筋：普通受力钢筋型号为HRB335；

桥梁支座：位于1号，2号和3号桥墩中心线上的永久支座采用板式橡胶支座(GJZ 500×800×104 mm3)；位于0号桥台和4号桥墩上、T梁端部横隔板中心线下的永久支座采用滑板式支座(GJZF4400×450×87 mm3)；位于1号，2号和3号桥墩上、T梁端部横隔板中心线下的临时支座采用硫磺砂浆浇筑，下设混凝土垫块，尺寸为400×450×104 mm3。

为便于后续分析，对桥梁横截面上的关键点进行标识，并对主梁进行编号，如图2所示。

2全桥实体有限元模型

2.1材料特性及本构关系

混凝土强度等级为C55。选用midas/FEA中总应变裂缝模型提供的多线性曲线作为混凝土受压时的本构关系，选用常量曲线作为混凝土受拉时的本构关系[6]，如图3所示。

预应力筋、普通钢筋的本构关系选用von Mises模型。预应力筋的屈服强度为1 860 MPa，弹性模量为1.95×105MPa；普通钢筋的屈服强度为335 MPa，弹性模量为2.0×105MPa，泊松比为0.3。

图3　混凝土的非线性本构关系Fig.3 Nonlinear constitutive relations of concrete

2.2荷载及边界条件

荷载主要考虑自重、预应力、二期恒载(如未参与结构受力的桥面现浇层和铺装层)等。结构自重以体积力的形式考虑；预应力采用等效节点荷载处理；二期恒载以面荷载的形式考虑[7]。

对于滑板式支座，约束其竖向和横向的线位移；对于临时支座和板式支座，约束其3个方向的线位移。

2.3预应力效应模拟

以张拉控制应力作为预应力筋的初始应力直接施加到预制T梁上，在桥梁全过程受力的不同阶段，预应力筋的真实应力为累积应力增量与其初始应力之和。上述预应力施加方法可有效计及成桥初始状态下材料的累积塑性变形，并能获得较为精确的成桥初始变形和应力状态。

2.4三维有限元模型

混凝土采用三维实体单元，钢筋采用植入式杆单元，以横桥向作为x轴、纵桥向作为y轴、竖直向为z轴，按实际尺寸建立全桥三维实体有限元模型。

3施工过程仿真分析及有限元模型验证

3.1施工过程仿真

桥梁上部结构的施工分为5个阶段：1)预应力混凝土T梁预制、预应力筋张拉；2)预应力混凝土T梁安装；3)墩顶、墩顶两侧18.0 m范围内的湿接缝及横隔梁浇筑，顶板预应力筋张拉；4)临时支座拆除及剩余湿接缝、横隔梁浇筑；5) 浇筑桥面现浇层，进行桥面铺装。

根据上述施工过程，运用midas/FEA有限元软件中单元的激活与钝化功能对各施工阶段进行定义和仿真模拟。对于在当前阶段激活的单元，初始状态为0；对于在前一阶段已激活单元，其当前阶段的初始内力为前一阶段分析得到的内力，通过计算最终得到成桥初始状态的内力。图4为上述各施工过程的有限元网格。

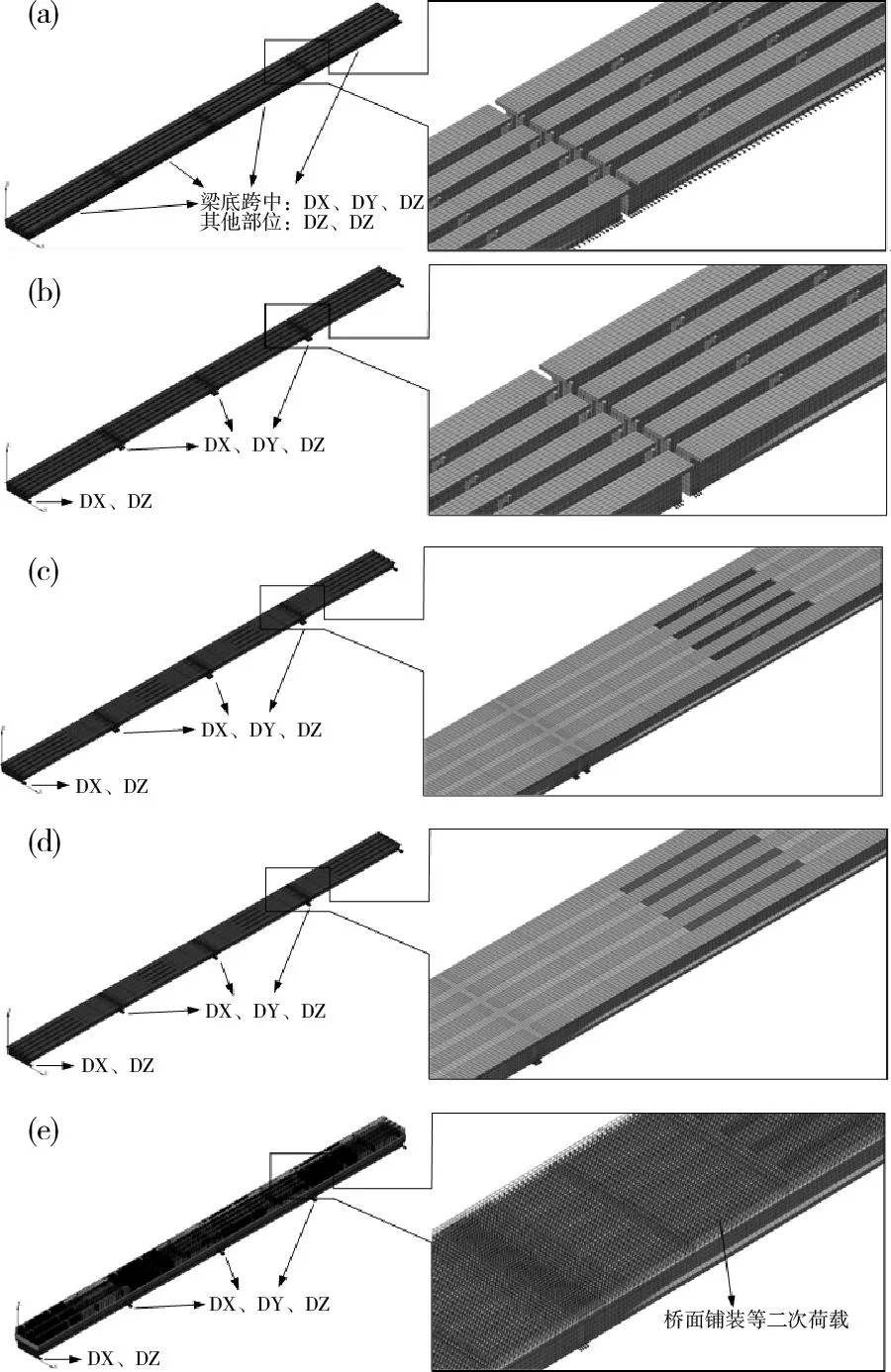
(a)第1阶段施工完毕时的有限元网格；(b)第2阶段施工完毕时的有限元网格；(c)第3阶段施工完毕时的有限元网格；(d)第4阶段施工完毕时的有限元网格；(e)第5阶段施工完毕时(初始状态)的有限元网格图4　桥梁上部结构不同施工过程的有限元网格Fig.4 Finite element mesh of bridge superstructure indifferent construction process

3.2成桥初始状态内力结果分析

根据成桥初始状态的有限元计算结果，采用Matlab绘制了横截面上关键点的von Mises应力沿纵桥向的分布图，见图5。

从图中可见：1)截面上所有关键点的应力均为正值，且沿纵桥向关于2号支座截面对称分布，上翼缘最大应力距桥台55 m左右，位于截面D点，值为10.47 MPa，下翼缘最大应力距桥台40 m左右，位于截面F点，值为14.67 MPa；2)截面上翼缘A，B，C和D点的应力沿纵桥向的变化趋势基本一致，中间支座及其两侧15 m范围内的应力呈锯齿状剧烈变化，其中B和D点的应力变化尤其明显，此外，支座处应力相对较小；3)在同一横截面位置，B点和D点的应力几乎相等，仅在中间支座两侧15 m范围内略有不同，并且二者均大于A点和C点的应力，C点的应力最小；4)截面下翼缘E和F点的应力沿纵桥向的变化趋势基本一致，在同一横截面上，F点的应力略大于E点的应力，在纵向同一点上，边跨应力明显大于中跨应力，支座附近应力除外。

出现上述现象的原因主要有：1)在成桥初始状态，结构和荷载沿纵桥向均关于2号支座截面对称，因此，截面上关键点的应力沿纵桥向同样关于2号支座截面对称；2)桥梁中间支座上翼缘两侧设有分批截断的负预应力钢筋，导致该区域混凝土的应力呈锯齿状剧烈变化，此外，支座处混凝土浇筑较晚，仅受板顶负预应力作用，因而应力较小；3)边梁和中梁板顶负预应力筋沿板顶纵向中心线对称分布且面积相等，因此，同一截面位于中心线上的B点和D点的应力几乎相等，并且大于截面上翼缘其它位置处的应力，由于边梁和中梁板顶负预应力筋截断位置略有不同，使得中间支座两侧15 m范围内B点和D点的应力略有不同；4)预制T梁梁底正预应力筋截面积的大小顺序为边跨边梁>边梁中跨>中跨边梁>中跨中梁，使得同一截面位置边梁梁底F点的应力大于中梁梁底E点的应力，而在纵桥向则表现为边跨内混凝土的应力大于中跨内混凝土的应力。

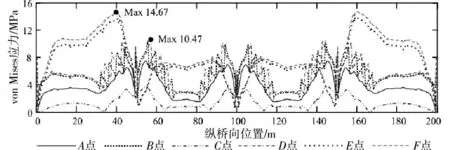
图5　桥梁横截面上关键点的von Mises应力沿纵桥向的分布Fig.5 Distribution along the longitudinal direction of thebridge of von Misesstress of the key point of the cross section

通过对西张村大桥主梁截面上、下缘的von Mises应力分析可知，成桥初始状态下桥梁截面关键点均处于受压状态，最大压应力14.67 MPa，说明在成桥初始状态桥梁未出现开裂或压碎破坏现象。此外，由上述分析可知，成桥状态桥梁初始应力的大小及其分布规律是合理的，表明本文所建立的有限元模型是正确的、合理的。

4极限承载力仿真分析

4.1荷载及加载工况

极限承载力分析时，以上节计算得到的成桥初始状态的内力作为初始条件，即极限承载力分析时只需在成桥初始状态的基础上再施加λ[8]倍的车道荷载即可。车道荷载取值分别为qk=10.5 kN/m(均布荷载)和Pk=360 kN(集中荷载)[7]。

取边跨跨中(1-1)截面、中跨跨中(2-2)截面及梁端近支点(3-3)截面(距0号桥台8 m，剪应力最大)为关键分析截面。两车道荷载沿横向分别考虑对称和偏载布置，沿纵向分别布置在使结构关键截面产生最不利效应的同号影响线上，共计6种加载工况。

工况1：初始状态+λ[均布荷载(偏载)+集中荷载(边跨跨中)]，①号主梁1-1截面正弯矩最大。

工况2：初始状态+λ[均布荷载(对称)+集中荷载(边跨跨中)]，直接受荷最多的②号或④号主梁1-1截面正弯矩最大。

工况3：初始状态+λ[均布荷载(偏载)+集中荷载(中跨跨中)]，①号主梁2-2截面正弯矩最大。

工况4：初始状态+λ[均布荷载(对称)+集中荷载(中跨跨中)]，直接受荷最多的②号或④号主梁2-2截面正弯矩最大。

工况5：初始状态+λ[均布荷载(偏载)+集中荷载(梁端近支点)]，①号主梁近支点3-3截面剪力最大。

工况6：初始状态+λ[均布荷载(对称)+集中荷载(梁端近支点)]，直接受荷最多的②号或④号主梁近支点3-3截面剪力最大。

4.2有限元计算结果及其分析

分别在上述6中工况下对该桥进行极限承载力计算，结果见图6~10。

(a)偏载工况下①号梁底关键截面；(b)对称荷载工况下④号梁底关键截面图6　梁底关键截面的荷载-竖向位移曲线Fig.6 Load-vertical displacement curve of beambottom key section

(a)偏载工况下①号梁关键截面；(b)对称荷载工况下④号梁关键截面图7　梁底关键截面预应力钢筋的荷载-拉应力曲线Fig.7 Load-tensile stress curve of the prestressedreinforced in the key section of beam bottom

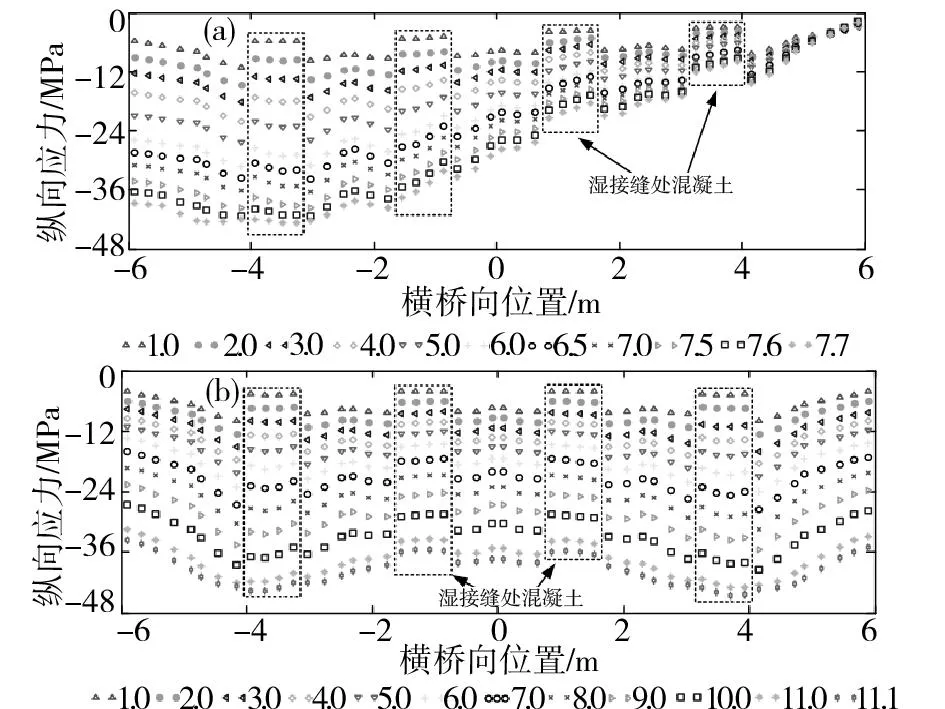
(a)工况1：偏载；(b)工况2：对称加载图8　1-1截面上缘混凝土纵向应力的横向分布情况Fig.8 Lateral distribution of vertical stress in the sectionon the edge of the concrete

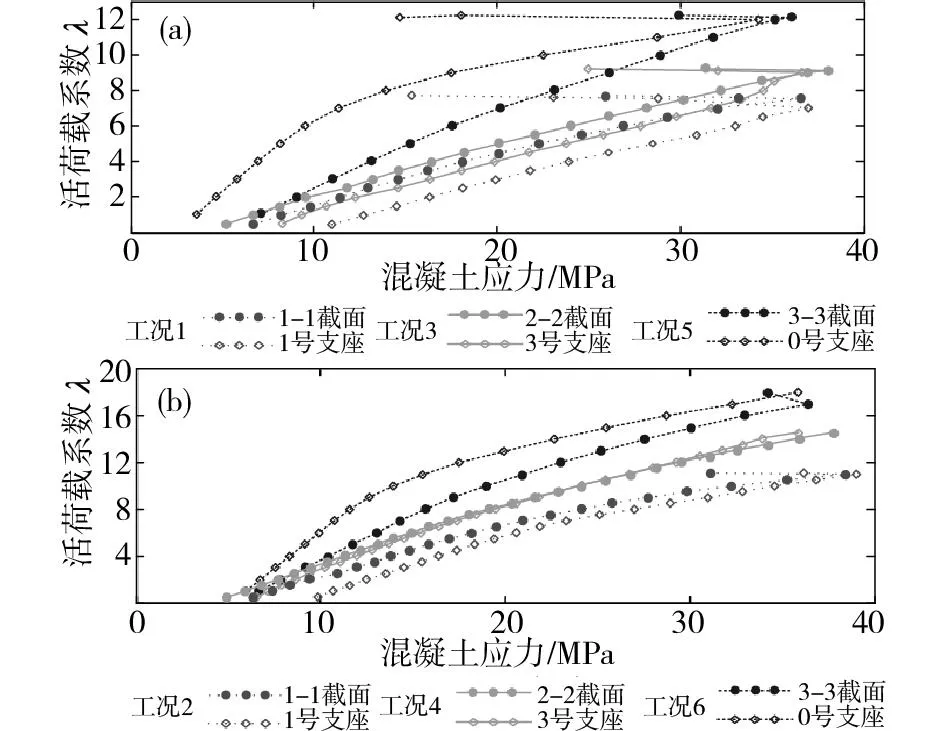
(a)偏载工况下①号梁；(b)对称荷载工况下④号梁图9　各工况下关键截面上缘、支座截面下缘中心线上混凝土的应力-荷载曲线Fig.9 Stress-load curve of the concrete in both topedge of a key section and down section bearing edgecenterline in different working condictions

(a)偏载工况下①号梁；(b)对称荷载工况下④号梁图10　各工况下关键截面下缘、支座截面上缘中心线上混凝土的应力-荷载曲线Fig.10 Stress-load curve of the concrete in both top edgeof a key section and down section bearing edge centerlinein different working condictions

4.2.1加载全过程分析

在梁底关键截面底部混凝土开裂之前，整个桥梁基本处于弹性工作状态。因此，梁底关键截面的竖向位移(图6)和梁底关键截面预应力钢筋的拉应力(图7)随λ的增加大致以线性方式增长，而梁底关键截面底部混凝土的应力(图10)先线性减小后线性增大，达到最大值时混凝土开裂，对应的活荷载系数可从图10得出；在梁底关键截面底部混凝土开裂之后、结构达到极限承载力之前，桥梁结构进入非线性受力阶段，因此，梁底关键截面的竖向位移(图6)和梁底关键截面预应力钢筋的拉应力(图7)随λ的增加曾加速增长趋势；当结构达到极限承载力状态时，随着活荷载系数的微弱增加，梁底关键截面的竖向位移(图6)和梁底关键截面预应力钢筋的拉应力(图7)均快速增长，曲线的斜率几乎为零，桥梁关键截面上缘、支座截面下缘中心线上的混凝土被压碎或达到极限应力状态，结构破坏时对应的活荷载系数可由图6和9综合判断得出，各工况下结构达到极限承载力时的活荷载系数见表1。

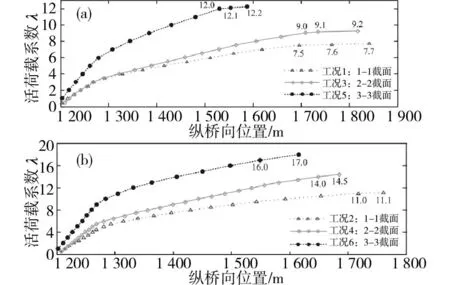
表1　各工况下结构达到极限承载力时的活荷载系数

从表1可见，当结构达到极限承载能力状态时，工况1，2和5对应的活荷载系数为7.5，9.0和12.0，分别小于工况2，4和6对应的活荷载系11.0，14.0和16.0，说明与对称加载工况相比，偏载工况下桥梁更容易发生破坏。

4.2.2混凝土应力的横向分布特征分析

以工况1、工况2为例，从图8(a)可以看出，在偏载作用下，1-1截面上缘纵向正应力沿横向分布十分不均匀，主要体现在2个方面：一是在同一荷载等级下湿接缝处混凝土的应力明显小于其两侧预制主梁混凝土的应力，这与施工阶段观察到的现象一致；二是直接受荷的边梁1-1截面上表面混凝土的应力较大，而非直接受荷的其他主梁1-1截面上表面混凝土的应力则大致线性减小；从图8(a)可以看出，在对称荷载作用下，同一荷载等级下湿接缝处混凝土的应力明显小于其两侧预制主梁混凝土的应力。

此外，从图8还可以看出，随着荷载等级的增加，预制主梁上缘的混凝土先于湿接缝处的混凝土达到极限应力状态，二者受力并不同步，这在一定程度上降低了桥梁结构的极限承载力。

4.2.3结构破坏特征分析

从图9(a)可以看出，在偏载工况下，结构的破坏形式表现为①号主梁相应的支座截面底部混凝土先被压碎，随后相应的关键截面顶板混凝土被压碎；从图9(b)可以看出，在对称荷载工况下，结构的破坏形式表现为④号主梁相应关键截面顶板的混凝土先达到极限应力状态或先被压碎，随后相应支座截面底部的混凝土被压碎。此外，从图7中可以看出，结构破坏时，主要承受拉力的关键截面底板和支座截面顶板中的预应力钢筋都没有达到屈服应力，并且从图8可以看出(偏载工况同工况1、对称加载工况同工况2)，在结构发生破坏时，桥梁的横向联系仍具有很强的传递荷载的能力，并未发生破坏。这表明在所有工况作用下，结构的破坏属于局部破坏，可以通过采取一定的措施对结构局部进行补强。

5结论

1)详述了考虑施工过程影响的先简支后连续梁桥三维实体有限元模型的建模方法，并由该模型精确地计算出桥梁成桥初始状态的内力，为后续极限承载力分析提供基准计算模型；

2)当结构达到极限承载能力状态时，工况1，2和5对应的活荷载系数为7.5、9.0和12.0，分别小于工况2，4和6对应的活荷载系数11.0，14.0和16.0，偏载工况下桥梁更容易发生破坏；

3)在偏载工况下，(边梁)①号主梁相应的支座截面底部混凝土先被压碎，随后相应的关键截面顶板混凝土被压碎；在对称荷载作用下，④号主梁相应关键截面顶板的混凝土先达到极限应力状态或先被压碎，随后相应支座截面底部的混凝土被压碎；

4)预制主梁上缘的混凝土先于湿接缝处的混凝土达到极限应力状态，二者受力不同步，这在一定程度上降低了桥梁结构的极限承载力。

参考文献：

[1] 姚玲森, 项海帆, 顾安邦. 桥梁工程[M].2版. 北京: 人民交通出版社, 2008.

YAO Lingshen, XIANG Haifan, GU Anbang. Bridge construction [M].2nd edition. Beijing: China Communications Press,2008.

[2] 陈淮, 陈鹏飞, 李杰. 钢构-连续组合梁桥主梁合拢关键技术[J]. 铁道科学与工程学报,2015,12(1):113-118.

CHEN Huai, CHEN Pengfei, LI Jie, Study on key technology of the main girder closure of rigid frame -continuous combination beam bridge[J]. Journal of Railway Science And Engineering,2015,12(1):113-118.

[3] 吴光宇, 林伟, 汪劲丰, 等. 有效预应力对大跨P.C.桥梁极限承载力的影响研究[J]. 计算力学学报, 2013, 30(3): 362-369.

WU, Guangyu, LIN Wei, WANG Jinfeng, et al. Influence of effective prestress on ultimate bearing capacity for large-span prestressed concrete bridge[J].Chinese Journal of Computational Mechanics,2013,30(3):362-369.

[4] 李静斌, 葛素娟, 陈淮. 先简支后连续分体式箱梁桥简支转连续施工方法研究[J]. 世界桥梁, 2010, 1(3): 12-15.

LI Jingbin, GE Sujuan, CHEN Huai. Study of construction schemes of transferring simply-supported structure to continuous separated box girder bridge[J]. Word Bridge,2010,1(3):12-15.

[5] 易锦, 贺国京, 陆杰. 合拢及体系转换顺序对多跨钢构-连续组合梁桥组合分析[J]. 铁道科学与工程学报, 2013,10(5):23-27.

YI Jin, HE Guojing, LU Jie. Impact analysis of closure order and system transformation order for bridges with rigid frame-combined continuous beam[J]. Journal of Railway Science and Engineering,2013,10(5):23-27.

[6] midas FEA分析与计算原理[M]. 北京迈达斯技术有限公司.

Midas FEA Analysis and Algorithm Manual[M]. MIDAS IT(Beijing)Co,Ltd.

[7] JTG D60—2004, 公路桥涵设计通用规范[S].

JTG D60—2004, Design of highway bridges and culverts[s].

[8] 吴光宇. 大跨P.C.桥梁非线性行为的分析理论及其极限承载力计算研究[D]. 杭州：浙江大学，2006.

WU Guangyu. The nonlinearity behavior analysis theory and ultimate bearing capacity calculating method for Large-span P.C.bridges[D]. Hangzhou: Zhejiang University, 2006.

[9] Davies J M．Strain hardening. Local buckling and lateral-torsioal buckling in Plastic hinges[J]．Journal of Constructional Steel Research, 2006，12(62):27-34.

[10] Mehmet Inel, HayriBaytan Ozmen．Effects of plastic hinge properties in nonlinear analysis of Reinforced concrete buildings[J]．Engineering Structures,2006，15(28):1494-1502.

[11] Luarent Caurffiez，Joseph Ciccotelli, Blaise Conrard. Design of intelligent distributed control systems. a dependability point of view [J]．Reliability Engineering and System Safety，2004，84(1): 19-32.

[12] Campbell T I, Venkatesh Kumar R Kour. Deformation controlled nonlinear analysia of prestressed concrete continuous beams[J]．PCI Journal, 1990，25(1):42-55.

[13] AlfarabiSharif G J, AISulaimaniand B N. Ghaleb Strengthening of initiallyloaded reinforced concrete beams using FRP plates[J]．ACI Structural Journal,1994，26(23):26-31.

[14] Zienkiewinz O C.The finite element method[M]．3rd edition. London: McGraw Hill, 1977:18-34.

[15] Engin Keyder.Friction losses in prestressed steel by equivalent load method[J]． PCI Journal, 1990, 26(2)：74-77.

(编辑阳丽霞)

摘要：为研究先简支后连续T梁桥从施工至极限破坏的全过程受力性能，以河南省省道S318线西张村大桥为工程背景，运用有限元软件midas/FEA建立同时考虑几何非线性和材料非线性影响的全桥三维实体模型，分别在6种工况下进行了仿真分析研究。研究结果表明：桥梁达到极限承载力时，偏载工况下的活荷载系数小于相应对称荷载工况下的活荷载系数；偏载工况下边梁相应的支座截面底部混凝土先被压碎，对称荷载作用下，受荷位置主梁相应关键截面顶板的混凝土先被压碎；预制主梁上缘的混凝土先于湿接缝处的混凝土达到极限应力状态，二者受力不同步。

关键词：先简支后连续T梁桥；极限承载力；有限元；全过程受力

Study on full loading process performance of simply supported continuous T-beam bridgeZHU Xiaoqing, CHEN Daiha, CHEN Huai

(School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China)

Abstract:The paper studied the stress performance of simply supported continuous T-beam bridge from construction stage to the ultimate failure. By considering the material and geometric nonlinear conditions, the finite element software Midas/FEA was used to simulate the three-dimensional solid model of a full-bridge under the six kinds of conditions in the engineering background of Xizhangcun Bridge in Henan Province Highway S318. The results showed that: The live load factor in unbalance loading working condition was less than that of balanced when the bridge reach the ultimate bearing capacity; The concrete in the bottom of support cross-section of the spandrel beam was crushed firstly in unbalance loading working condition; In the condition of balance loading working the concrete in the top of the key sections of girder at the load position was crushed firstly; The concrete at the top of the girder precast reached the critical stress earlier than in the wet-joint and their force were asynchronous.

Key words：simply supported continuous T-beam bridge; ultimate bearing capacity; finite element; full loading process

中图分类号：U448.14

文献标志码：A

文章编号：1672-7029(2016)01-0089-07

通讯作者：陈淮(1962-)，男，河南淮阳人，教授，博士，从事桥梁工程研究；E-mail: chenh@zzu.edu.cn

基金项目：国家自然科学基金资助项目(51408555)；河南省交通运输厅科技项目(2008P250)

收稿日期：*2015-06-24