考虑竖向地震效应的边坡地震永久位移计算图表
考虑竖向地震效应的边坡地震永久位移计算图表
王曙光1,何光槐2,汤祖平3,王志斌4,赵炼恒5
(1.贵州省交通规划勘察设计研究院股份有限公司,贵州 贵阳 550003;
2.中交第四航务工程局有限公司,广东 广州 510290;
3.上海市政工程设计研究总院(集团)有限公司深圳分公司,广东 深圳 518013;
4.湖南科技大学 土木工程学院,湖南 湘潭 411201;
5.中南大学 土木工程学院,湖南 长沙 410075)
摘要:基于极限分析上限法和Newmark刚塑性滑块模型,推导考虑水平与竖向地震效应下,对数螺旋线型滑面边坡屈服加速度和边坡永久位移的计算公式;采用序列二次规划法编制非线性规划迭代程序对边坡地震永久位移计算模型进行优化求解,由此探讨竖向地震对边坡永久位移的影响规律。算例分析证明了本文方法的正确性。在此基础上,绘制边坡屈服加速度、位移系数以及4个典型地震加速度时程的2次积分图表,以便于边坡地震永久位移的查表计算。并给出具体算例,说明采用本文表格进行查表计算的流程。
关键词:边坡;地震永久位移;竖向地震效应;Newmark法;极限分析上限法
地震作用下边坡的稳定性评价指标主要有2种:边坡安全系数和永久位移。目前,采用单一的边坡抗震安全系数评价边坡动力稳定性的不足己经得到普遍认同。边坡的地震永久位移量化了边坡受损程度,为坡体稳定性判识提供了另一种可靠依据,成为边坡工程抗震设计的发展趋势。其中,以Newmark于1965年提出的刚塑性滑块模型为估算地震永久滑移量的方法较为简便实用[1],已广泛地应用于土石坝、边坡、挡土墙、城市固体废物填埋场等土工建筑物的抗震稳定性评价中[2-3]。地震影响效应下,岩土体强度参数等出现明显劣化。李红军等[4]考虑土的抗剪强度在地震过程中的波动效应,在动强度的基础上将拟静力极限平衡分析与地震动力反应相结合,进行土工建筑物永久位移分析,并通过算例表明,考虑动强度效应得到的永久位移约为采用静强度的2~3倍。栾茂田等[5]采用剪切条模型进行堤坝动力分析,确定堤坝的地震响应,进而基于对数螺旋面破坏机制及由此所确定的屈服加速度系数,运用Newmark计算模型进行分析,考虑土的强度参数随滑坡体最大深度和堤坝高度之比等因素对滑坡体的屈服地震加速度和平均地震加速度之比沿深度分布的影响,建立了堤坝地震滑移量的经验估算模式。Jin等[6-8]则将研究拓展至考虑随机可靠度、水力影响效应、与其他随机振动效应耦合等复杂条件的相关研究。以上研究均未考虑地震竖向震动效应的影响,但实际上岩土边坡在受地震影响效应过程中,同样受到明显的水平地震效应。如Northridge地震[9](1994,震级6.7)、Kanto 地震[10](1923,震级7.9)和Kobe地震[11](或称Osaka-Kobe地震,Hanshin地震,1995,震级7.2)的地震谱记录都表明震中部位的竖向加速度峰值往往也较大,可超过水平向加速度峰值的50%。因此竖向地震效应对边坡抗震性能影响的研究也日益受到学者们的重视和关注[12-15],但对是否需要考虑竖向地震效应分析地震对边坡永久位移的影响尚有一定争议[16-17]。基于以上原因,本文基于极限分析上限法和Newmark刚塑性滑块模型,推导获得了可考虑水平与竖向地震共同效应对边坡地震永久位移的计算模型,并进行了优化求解,探讨了竖向地震对边坡永久位移的影响规律。在此基础上,绘制了便于简单均质边坡地震永久位移的设计计算图表,并给出了具体分析算例。

1边坡地震永久位移计算极限分析上限法
1.1基本假定及破坏模式
为了简化研究对象,本文在参考有关研究成果的基础上,应用如下基本假设:
1)按平面应变问题进行分析;2)边坡岩土体为理想刚塑性体,服从M-C强度准则,遵循相关联流动法则;3)不考虑岩土体孔隙水压力作用,也不考虑岩土体抗剪强度参数c和φ因地震荷载作用而产生变化;4)主应力轴和主应变轴重合;5)采用拟静力法分析水平向、竖向地震作用效应。尽管考虑到竖向地震较少与水平向地震同时达到加速度峰值[10],但此处为简化计算,将竖向地震拟静力值等效为水平向地震拟静力值的一个分量,即:kv=λkh,λ为kv相对于kh的比例系数。其中,kv和kh分别为竖向地震系数和水平向地震系数。
已有研究成果表明[10,18]:简单均质土坡的破坏面更接近对数螺旋面形状,因此本文也采用这种旋转破坏机构为例对边坡地震永久位移进行分析。其破坏机构如图1所示。

(a)破坏机理;(b)位移模式图1 边坡旋转破坏机构Fig.1 Rotational failure mechanism of slope
其中旋转机构破坏面为对数螺旋方程面,可表示为:
r=r0·e(θ-θ0)·tanφ
(1)
式中:θ0和θ为描述螺旋线破坏机构的角度参数;r为与θ定义的极径;r0为θ=θ0的极径;φ为土体内摩擦角;H为坡高,m;β为土坡倾斜角;kv=av/g,kh=ah/g,av和ah分别为竖直和水平地震加速度,g为重力加速度;其他参数含义见图1,根据螺旋线破坏面的几何关系有:
(2)
(3)
1.2能耗计算
在地震的作用下,外功率主要有滑体重力和地震力引起的,而坡体内的内能耗散功率主要由沿滑面的土体内能耗散功率组成。
1.2.1外功率
自重功率:
(4)
竖直地震引起的功率:
(5)
水平地震引起的功率:
(6)

(sinθh+3tanφcosθh)e3(θh-θ0)tanφ
(7)

(8)
(9)
(3tanφsinθh-cosθh)e[3(θh-θ0)tanφ]
(10)
(11)
(12)
1.2.2内部功率
内部耗散率发生在间断面BC上。依据相关联流动法则,沿间断面BC能量耗散率的积分,可以由该面微分dθ/cosφ与黏聚力c以及该面上切线间断速度(vcosφ)乘积得到(Chen,1975[18])。沿整个间断面积分,即可得到总的内部能量耗散率:
(13)
式中:v为速度间断量且v=ωr0e(θ-θ0)tanφ。
1.3边坡屈服加速度
当均匀边坡处于临界状态时,以水平地震加速度系数kh表征的地震荷载效应参数恰好达到临界屈服加速度kc,由功率平衡方程可得:
(14)
均匀边坡的临界屈服加速度kc可由式(14)求出,如下所示:
(15)
对于给定的边坡和给定的比例系数λ(即边坡倾角β、内摩擦角φ、无量纲系数c/γH、地震比例系数λ为已知),由式(15)可以看出:kc是θ0和θh2个未知参数的函数kc(θ0,θh)。当θ0和θh满足条件:
∂kc/∂θ0=0、∂kc/∂θh=0
(16)
时,函数kc(θ0,θh)取得一个极值,进而获得边坡屈服加速度kc的一个上限解答。基于数学软件MATLAB平台,本文采用序列二次优化法对函数kc(θ0,θh)进行了优化求解,其数学规划表达式为:
minkc=kc(θ0,θh)
(17)
(18)
常规岩土参数条件下,简单边坡动力稳定性拟静力分析的屈服加速度kc计算结果如图2所示。
1.4边坡在地震作用下产生的永久位移计算

(19)
结合式(15)和(16)可得:

(20)
式中:l为滑动体重心到转动圆心O点的距离;G为滑体的重力大小,可以通过简单计算获得:
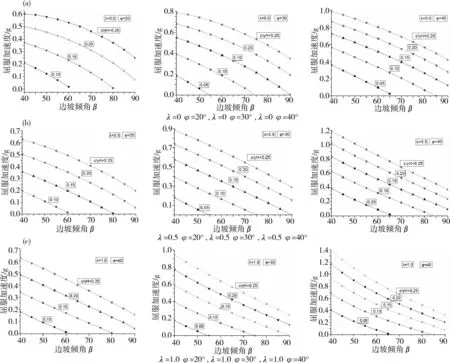
(a)λ=kv/kh=0.0;(b)λ=kv/kh=0.5;(c)λ=kv/kh=1.0图2 边坡水平屈服加速度Fig.2 Horizontal yield acceleration of slopes
(21)
由于滑体重力和地震力所做功率分别如下:
重力功率:
(22)
水平地震力功率:
(23)
竖直地震力功率:
(24)
因此,联立上述3式,可求得l为:
(25)
由式(19)可以看出,坡体的转动加速度是一个与作用在坡体上的地震水平加速度有关的函数。在确定出坡体地震屈服加速度后,对式(20)进行二次积分,便可得到滑块ABC的累计转动滑移量,因此,通过几何关系可求得边坡坡脚的水平永久位移:

(26)
式中C为位移系数:
(27)
当λ确定以后,对于一个给定的边坡(β,φ,c/γH),由式(15)可优化出屈服加速度kc,并可确定最危险滑裂面(θ0,θh),将其代入式(27)即可确定地震位移系数C。由此可知,地震位移系数C可由4个参数(λ,β,φ和c/γH)确定。屈服加速度kc也可表示为参数(λ,β,φ和c/γH)的函数,故地震位移系数可以方便地表示为参数(λ,β,φ和kc)的函数。
简单边坡常规岩土参数条件下,边坡动力稳定性拟静力分析时,对于给定的(λ,β,φ和kc),可以给出地震位移系数C的图如图3所示。

(a)λ=kv/kh=0.0;(b)λ=kv/kh=0.5;(c)λ=kv/kh=1.0图3 边坡位移系数CFig.3 Displacement coefficient C of slopes
2边坡地震永久位移图表
为便于工程实际,选取4个比较典型的地震数据(Northridge1994,Kobe 1995,Imperial Valley1940,CHICHI 1999)各地震的信息如表1所示。对其加速度-时程曲线成比例的增大或者减小,得到一系列相同形式的加速度-时程曲线,然后对它们按式(25)进行2次积分,其结果便可表示为k-kc和km的函数,如图4所示。则对于给定的边坡,由图2和图3可查出边坡的屈服加速度kc和地震位移系数C,然后通过图4查出的地震位移乘以地震系数C就可得到边坡永久位移。

表1 地震信息
注:PGA峰值加速度,PGV峰值速度,PGD峰值位移,Pref.Vs30为场地地下30 m平均剪切波速度。

(a)Northridge地震;(b)Kobe地震;(c)Imperial Valley地震;(d)CHI-CHI地震图4 地震波2次积分后得到的位移Fig.4 Displacement resulting from two integral of seismic wave
为说明此图表的作用,选取边坡算例,边坡参数为:边坡倾角β=45°,高度H=15 m土体内摩擦角φ=20°,c=15 kN/m2,γ=20 kN/m3,λ=0.5。在地震永久位移计算中以Kobe地震记录为例,将其地震波的加速度-时程曲线成比例增大,并使它们的峰值加速度增大到0.4g。首先,通过计算可得c/γH=0.106,由图2可查得边坡的屈服加速度kc为0.17g,然后通过图3查得地震位移系数C=1.47,由km-kc=0.43,由图4可查出其加速度时程曲线的2次积分为5.02 cm,则边坡坡脚的水平永久位移为:1.47×5.02=7.18 cm。
3对比验证与参数分析
3.1算例分析
基于数学软件MATLAB平台,采用序列二次优化法对函数kc(θ0,θh)进行了优化求解,并依据优化得到的滑裂面参数(θ0,θh)。为了验证本文公式和程序的正确性,选取Liangzhi You(1999)[3]中的算例结果与本文的结果进行对比,边坡算例参数为:坡倾角β=55°,坡高H=18m,重度γ=17 kN/m3,黏聚力c=15.3 kN/m2,内摩擦角φ=36°。
对该边坡输入如图5所示的Northridge(1994)的水平方向的地震波,其加速度峰值为286.5 cm/s2,时间步长为0.02。当只输入水平地震波时则λ=0。计算得到的边坡永久位移为4.201 1 cm,与Liangzhi You(1999)[3]文中的计算结果4.2 cm基本一致,这说明了本文公式和所编程序的正确性。且求得滑裂面参数(θ0,θh)=[53.356°,98.81°],计算所得的边坡角速度-时程和位移-时程图如图6~7所示。

图5 1994年Northridge水平方向的地震记录(记录地点:Moorpark)Fig.5 Horizontal ground acceleration of Northridge 1994earthquake records (Moorpark Station)

图6 边坡的速度-时程图Fig.6 Angular velocity of slopes against times
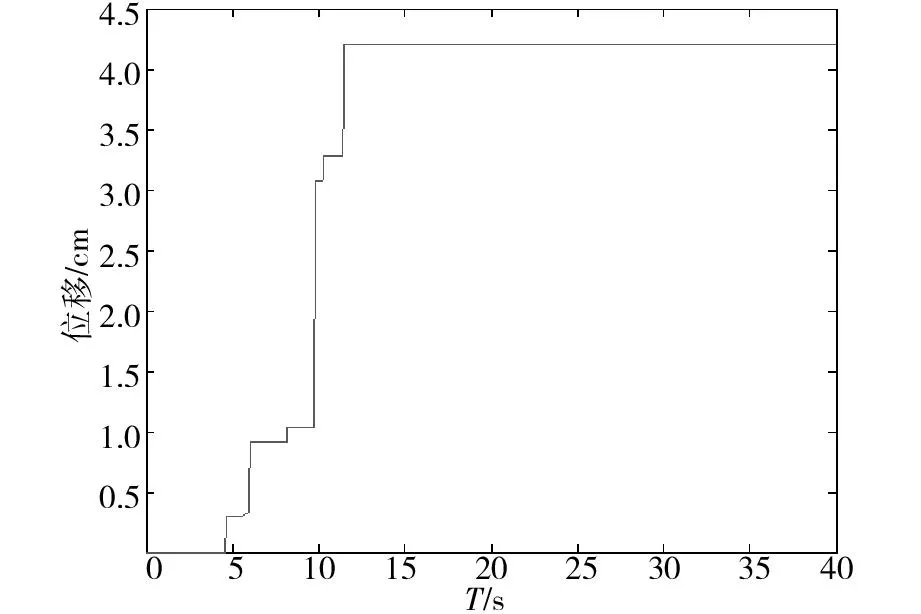
图7 边坡的永久位移-时程图Fig.7 Permanent displacement of slopes against times
3.2竖向地震对边坡永久位移的影响
为了分析竖直和水平地震加速度的比例系数λ对永久位移的影响,选取Liangzhi You(1999)[3]文中的算例,并取λ=-1.0~1.0,求得边坡永久位移如图8所示。

图8 边坡的永久位移随比例系数λ变化Fig.8 Permanent displacement of slopesagainstscale factor λ
由图8可知,边坡永久位移与比例系数λ的增大而增大,呈现出非线性增大趋势。且当λ=-1.0和1.0的时候,坡脚水平地震累计位移分别为2.16 cm和7.37 cm,分别与λ=0的地震位移4.20 cm相差48.5%和75.5%,说明竖向加速度对简单均质边坡永久位移的影响不容忽略。
4结论
1)基于极限分析上限法和Newmark刚塑性滑块模型,推导出了考虑水平与竖向地震效应下,对数螺旋线型滑面边坡屈服加速度kc和边坡永久位移的计算公式;采用序列二次规划法编制了非线性规划迭代程序对边坡地震永久位移计算模型进行优化求解,由此探讨了竖向地震对边坡永久位移的影响规律。
2)绘制了边坡屈服加速度、位移系数以及4个典型地震加速度时程的两次积分图表,以便于边坡地震永久位移的查表。并给出了采用本文表格进行查表计算的流程。
3)参数分析显示边坡永久位移随比例系数λ的增大而增大,呈现出非线性增大趋势,表明竖向加速度对简单均质边坡永久位移的影响不容忽略。
参考文献:
[1] Newmark N M. Effects of earthquakes on dams and embankments[J]. Geotechnique, 1965, 15 (2):139-160.
[2] Cai Z, Bathurst R J. Deterministic sliding block methods for estimating seismic displacements of earth structures[J]. Soil Dynamics and Earthquake Engineering, 1996, 15(4):255-268.
[3] You L Z, Michalowski R L. Displacement charts for slopes subjected to seismic loads[J]. Computers and Geotechnics, 1999, 25(1): 45-55.
[4] 李红军,迟世春. 基于动强度模式和时程应力分析的Newmark滑块位移法[J].岩土力学, 2006, 27(增刊): 1063-1068.
LI Hongjun, CHI Shichun. Effects of dynamic shear strength and time-histories stress analysis on newmark sliding block analyses [J].Rock and Soil Mechanics, 2006, 27(Supplement):1063-1068.
[5] 栾茂田,金崇磐,林皋. 非均布荷载作用下土坡的稳定性[J]. 水利学报, 1990(1):65-72.
LUAN Maotian, JIN Chongpan, LIN Gao. Stability of soil slopes under non-uniform explosion loading[J]. Journal of Hydraulic Engineering, 1990(1):65-72.
[6] Jin Man Kim, Nicholas Sitar. Probabilistic evaluation of seismically induced permanent deformation of slopes[J]. Soil Dynamics and Earthquake Engineering, 2012, 44(1): 67-77.
[7] 黄帅, 宋波, 牛立超, 等.地震作用下动孔隙水压力对边坡永久位移影响的简便计算方法[J].建筑结构学报,2014,35(3):215-221.
HUANG Shuai,SONG Bo,NIU Lichao, et al.Simple calculation method of permanent displacement of slope influenced by dynamic pore water pressure under earthquake[J]. Journal of Building Structures, 2014, 35(3): 215-221.
[8] 邓学晶,林倩,亓玉成,等. 平稳随机激励下耦合Newmark滑移系统的可靠性分析[J].计算力学学报, 2014, 31(5):578-583.
DENU Xuejing, LIN Qian, QI Yucheng, et al. Dynamic reliability analysis of the coupled Newmark sliding system under stationary random excitation[J]. Chinese Journal of Computational mechanics, 2014, 31(5):578-583.
[9] Stewart J P,Bray J D,Seed R B,et al. Preliminary report on the principal geotechnical aspects of the January 17,1994 Northridge earthquake[R]. Berkeley:Report UCB/EERC-94/08. Earthquake Engineering Research Center,University of California at Berkeley, 1994.
[10] Nouria H,Fakher A,Jones C J F P. Evaluating the effects of the magnitude and amplification of pseudo-static acceleration on reinforced soil slopes and walls using the limit equilibrium Horizontal Slices Method[J]. Geotextiles and Geomembranes, 2008, 26(4): 263-278.
[11] Leshchinsky D,Ling H I,WANG Juipin,et al. Equivalent seismic coefficient in geocell retention systems[J]. Geotextiles and Geomembranes, 2009, 27(1): 9-18.
[12] 刘红帅,薄景山,刘德东. 岩土边坡地震稳定性分析研究评述[J]. 地震工程与工程振动, 2005, 25(1):164-171.
LIU Hongshuai, BO Jingshan, LIU Dedong. Review on study of seismic stability analysis of rock-soil slopes[J].Earthquake Engineering and Engineering Vibration, 2005, 25(1):164-171.
[13] 赵炼恒, 李亮, 杨峰, 等. 加筋土坡动态稳定性拟静力分析[J]. 岩石力学与工程学报, 2009, 28(9): 1904-1917.
ZHAO Lianheng, LI Liang, YANG Feng, et al. Dynamic stability pseudo-static analysis of reinforcement soil slopes [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(9): 1904 -1917.
[14] Zhao Lianheng, Li Liang, Lin Yuliang, et al. Seismic stability quasi-static analysis of homogeneous rock slopes with Hoek-Brown failure criterion[C]// Wuhan: The Fifth National Symposium of Earthquake Prevention and Disaster Reduction, 2010.
[15] 罗强,赵炼恒,李亮,等. 地震效应和坡顶超载对均质土坡稳定性影响的拟静力分析[J].岩土力学, 2010, 31(12): 3835-3841.
LUO Qiang, ZHAO Lianheng, LI Liang, et al.Quasi-static stability analysis of homogeneous soil slopes under effect of surcharge and earthquake[J]. Rock and Soil Mechanics, 2010, 31(12): 3835-3841.
[16] 黄建梁,王威中,薛宏交. 坡体地震稳定性的动态分析[J]. 地震工程与工程振动, 1997, 17(4):113-122.
HUANG Jianliang, WANG Weizhong, XUE Hongjiao. Dynamic analysis of seismic stability of slopes[J]. Earthquake Engineering and Engineering Vibration, 1997, 17(4):113-122.
[17] Jacques Ingles. Effects of the vertical component of ground shaking on earthquake-induced landslipe displacement using generalizedNewmarkanalysis[J]. Engineering Geology, 2006, 86:134-137.
[18] Chen W F. Limit analysis and soil plasticity[M].Elsevier Science, Amsterdam, 1975.
(编辑阳丽霞)
Design tables of seismic permanent displacement for soil slope considering the vertical earthquake effectWANG Shuguang1, HE guanghuai2, TANG Zuping3, WANG Zhibin4, ZHAO Lianheng5
(1. Guizhou Transportation Planning Surver and Design Academy Co., Ltd, Guiyang 550003, China;
2. CCCC Fourth Harbor Engineering Co., Ltd., Guangzhou 510000, China;
3. Shanghai Municipal Engineering Design Intitute (Group) Co., Ltd - Shenzhen Branch, Shenzhen 518013, China;
4. School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China;
5.School of Civil Engineering,Central South University, Changsha 410075, China)
Abstract:The formulas of yield acceleration and permanent displacement of slopes against logarithmic spiral failure surface are deduced considering horizontal and vertical seismic effect based on upper bound limit analysis and Newmark rigid-plastic sliding block model. The nonlinear programming iteration procedure is compiled to calculate the optimal solution of slope seismic permanent displacement by adopting sequential quadratic programming, thus the influence rule of vertical earthquake on the slope permanent displacement is studied. Example analysis proves the correctness of this method. On this basis, graphs of yield acceleration, displacement coefficient and the two integral tables of four typical earthquake acceleration time history are drawn, which make it easy to get the seismic permanent displacement. And calculation process of adopting this article tables is illustrated by a specific example.
Key words:slope; seismic permanent displacement; vertical seismic effect; Newmark method; upper bound limit analysis
中图分类号:TU435
文献标志码:A
文章编号:1672-7029(2016)01-0055-08
通讯作者:赵炼恒(1980-),男,湖南益阳人,副教授,博士,从事道路与铁道工程、岩土极限分析理论与应用方面的教学与科研工作;E-mail:zlh8076@163.com
基金项目:国家自然科学基金资助项目(51208522);湖南省科学技术厅科技资助项目(2012SK3231,2012TT2039)
收稿日期:*2014-10-20

