基于图像不同亮度区域特征的Gamma矫正方法

丁 毅，李玉惠，李 勃

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

基于图像不同亮度区域特征的Gamma矫正方法

丁 毅，李玉惠，李 勃

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

在图像处理领域中，图像亮度不均会大大降低图像分割的正确性。为了有效弱化图像亮度不均对图像分割带来的影响，对处理图像亮度不均具有优势的Gamma矫正方法及各种改进方法进行了对比分析。针对现有Gamma矫正方法对图像高光区矫正效果的不佳，文中提出了类余切Gamma矫正函数和椭圆非线性矫正模型。实验结果表明，按图像像素值对图像分区，该方法不仅保持了现有Gamma矫正方法对阴影区和过渡区亮度处理的效果，而且缩小了图像高光区的像素取值范围，提高了对图像高光区矫正的效果，有效降低了整幅图像亮度的比例，在一定程度上使图像亮度分布更加均匀。同时，该方法具有较好的普适性，在处理其他亮度比例较大的图像时，该方法可以较好地均衡图像亮度的分布，在某些特殊场景下会大大提高图像分割的正确性和准确率。

图像处理;类余切Gamma矫正函数;椭圆非线性矫正模型;亮度不均;图像分割

0 引 言

由于客观环境通常使得获取的图像亮度分布不均匀，对以图像内容理解为目标的图像分割、目标跟踪等研究和应用造成较大的困难。因此，有效弱化图像亮度不均带来的影响，是图像内容理解研究中不可缺少的预处理环节，这也是计算机视觉中尚未有效解决的技术难点之一[1]。

为了有效解决图像亮度不均对图像分割带来的影响，近年来众多研究者提出了一些方法，如直方图均衡化方法[2]、色彩空间转换方法[3]、色感一致性方法[4]、色彩相似度方法[5]和改进的Gamma矫正方法[6-9]等。直方图均衡化方法虽然可以改善图像质量，但往往会在均衡后给图像带来一些不连续的斑块；色彩空间转换方法没有解决色彩通道之间的相关性问题；色感一致性方法存在精确估计光源位置的困难；色彩相似度方法对光照剧烈变化较为敏感[10]。相比之下，Gamma矫正是对图像像素值进行的矫正，矫正后不会给图像带来不连续的斑块，同时也不需要考虑光源位置，以及色彩通道之间的相关性问题，从而在处理图像亮度不均方面表现出一定优势[11]。但是，现有Gamma矫正方法在处理亮度比例较大的图像时，存在对高光区矫正程度的不足。

文中对多种改进的Gamma矫正方法进行了分析，结合不同亮度区域的特征，对高光区采用了类余切Gamma矫正函数和椭圆非线性矫正模型，使得整幅图像的亮度得到更好的均衡。

1 Gamma矫正方法

针对现有Gamma矫正方法处理亮度比例较大图像的不足，文中在文献[12]的基础上，对图像阴影区和过渡区采用类余弦Gamma矫正函数，保持对阴影区和过渡区的矫正效果。对图像高光区，采用类余切Gamma矫正函数矫正像素值的分布趋势，采用椭圆非线性矫正模型矫正像素的取值范围，使得整幅图像的亮度得到更好的均衡。

1.1 类余切Gamma矫正函数

将像素值区间分为阴影区、过渡区和高光区，具体范围为[0,x0],[x0,x1],[x1,255]，E1,E2,E3分别代表这三个区间。令p代表像素值区间[0,255]，Ω代表角度值区间[0,π]，Γ代表Gamma值区间，x代表像素值。取x1=x0+(255-x0)/n，n为区间[x0,255]的等分数，x0和n的值可根据实际情况而定，一般x0取中点。则p到Ω的线性映射定义为：

φ:p→Ω;Ω={ω|ω=φ(x)}

φ(x)=

(1)

其中，p到Γ的映射定义为：

h：p→Γ；Γ={h|h=h(x)}

因此，改进的f1(x)函数的表达式如下：

(2)

式中，λ∈(0,+∞)是调节矫正后图像Gamma取值范围的参数。

文献[12]在处理图像阴影区和过渡区方面，已经取得了较好的效果；但是，对高光区处理效果不佳。因此，文中针对图像高光区改进了函数f1(x)，如式(2)所示；对文献[12]中的函数f2(x)和f3(x)做了相应调整，使它们只对改进的函数f1(x)在处理图像阴影区和过渡区方面起到修正的作用。则重新定义的f2(x)和f3(x)的表达式如下：

(3)

(4)

式中的相关变量说明见文献[12]。因此，Gamma值矫正函数定义如下：

h(x)=f1(x)+f2(x)+f3(x)

(5)

取像素值矫正函数[3]：

g(x)=255(x/255)1/h(x)

(6)

所以，当a=0.6,b=0.3,n=5,λ=1时，g(x)曲线图如图1所示。

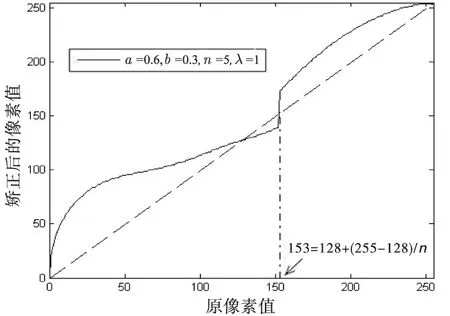
图1 g(x)曲线图

图1表明，对图像高光区即区间[153,255]的矫正，只矫正了像素值的分布趋势，仍然没有缩小高光区像素的取值范围。所以，在类余切Gamma矫正函数处理的基础上，还需要对图像高光区的像素取值范围进行矫正。

1.2 椭圆非线性矫正模型

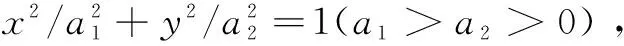
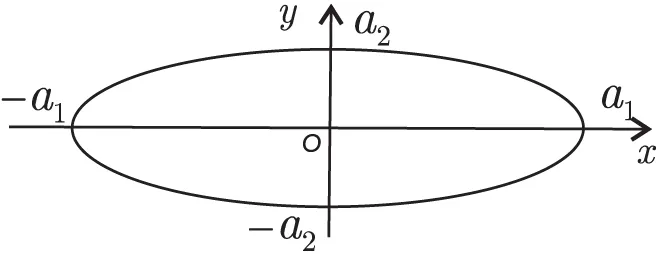
图2 椭圆曲线

p(x)=b(1-g1(x)/a)

(7)

矫正后g(x)的表达式如下：

(8)

式中，参数q是为了得到一条连续的像素值矫正曲线，使区间E2,E3对应的像素值平滑地衔接而被定义的。

q定义如下：

q=g1(x1+1)-g1(x1)

(9)

因此，矫正后g(x)的曲线图如图3所示。

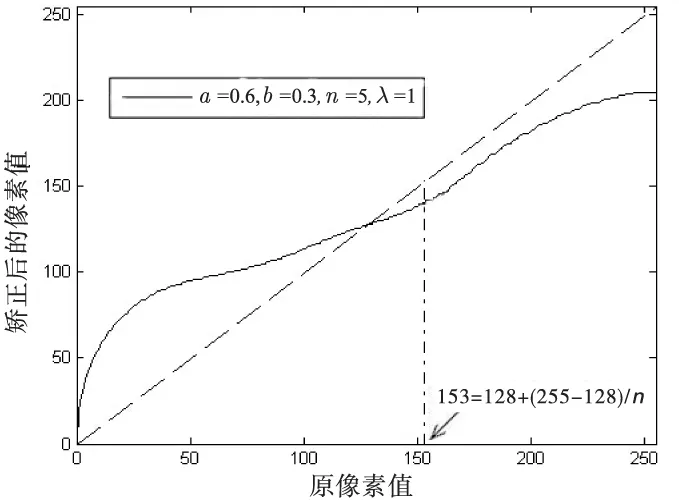
图3 矫正后的g(x)曲线图

图3表明，文中方法与现有Gamma矫正方法相比，保持了现有Gamma矫正方法对阴影区和过渡区亮度的处理效果，缩小了图像高光区像素的取值范围，有效降低了图像亮度的比例，使整幅图像亮度得到了更好的均衡。同时，图1和图3表明，采用椭圆非线性矫正模型对g(x)进行矫正，具有随着像素值增大，矫正值缓慢减小的特点，合理控制了高光区像素的取值范围，一定程度上抑制了因矫正引起的图像失真。

函数f1(x)第二部分的λ参数起到了合理控制矫正后Gamma取值范围的作用，使得对高光区的矫正有了自适应的特点。当λ选取不同参数时，Gamma值矫正曲线图和g(x)曲线图如图4所示。

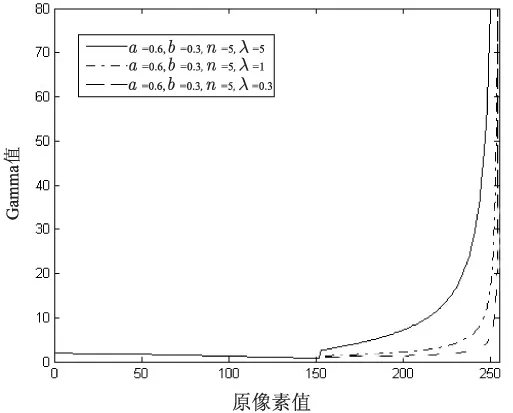
(a)Gamma值矫正曲线图

(b)g(x)曲线图

图(a)表明，λ的取值越大，矫正后的Gamma值就越大，从而对高光区矫正程度就越深，图像亮度的比例也就变得越小，效果如图(b)所示。但是，随着λ的增加，矫正后的图像亮度比例就会减小，矫正后的图像失真度也就会越大。因此，对于亮度比例不同的图像，λ取值也不相同。

2 实验结果分析

文中的实验图像来自国家教育考试标准化考场监控图像，具有亮度比例较大的特点。在同一环境下，对文中方法、文献[12-14]的方法进行了对比实验。在取较佳参数的情况下，实验效果如图5所示。

图5 不同方法处理后的效果图

图5表明，与现有Gamma矫正方法相比，文中所提出的方法保持了现有Gamma矫正方法对阴影区和过渡区亮度的处理效果，又缩小了高光区像素的取值范围，有效降低了图像亮度的比例，使整幅图像达到了更好的亮度均衡。

3 结束语

文中对多种改进的Gamma矫正方法进行了对比分析，提出了类余切Gamma矫正函数和椭圆非线性矫正模型对图像高光区进行矫正，并与文献[12-14]的方法进行对比实验。结果表明文中方法的有效性。

文中方法和其他Gamma矫正方法一样存在如何自动地、无监督地选取参数组合值的问题。因此，后续将会对这一问题做更深入的研究，从而提高文中方法的广泛实用性。

[1] 刘 培,王建英,尹忠科.图像光照补偿方法的研究[J].系统工程与电子技术,2008,30(7):1343-1346.

[2]ShenH,SunS,LeiB,etal.Anadaptivebrightnesspreservingbi-histogramequalization[C]//ProceedingsofSPIE.[s.l.]:[s.n.],2011.

[3]QaziImtnan-UI,AlataO,BurieJean-Christophe,etal.Choiceofapertinentcolorspaceforcolortexturecharacterizationusingparametricspectralanalysis[J].PatternRecognition,2011,44(1):16-31.

[4]FinlaysonG,FuntB,BarnardJ.Colorconstancyunderavaryingillumination[C]//Proceedingsofinternationalconferenceoncomputervision.WashingtonDC,USA:IEEEComputerSocietyPress,1995:720-725.

[5]SorianoM,MartinkauppiB,HuovinenS.Skindetectioninvideounderchangingilluminationconditions[C]//Proceedingsofinternationalconferenceonpatternrecognition.Barcelona:[s.n.],2000:839-842.

[6] 郑东亮,达飞鹏.提高数字光栅投影测量系统精度的gamma校正技术[J].光学学报,2011,31(5):116-121.

[7] 肖焱山,曹益平,武迎春,等.基于傅里叶频谱分析的相位测量轮廓术系统Gamma非线性校正方法[J].光学学报,2012,32(12):172-177.

[8] 王志国,梁志虎,刘纯亮.一种应用于ACPDP的反gamma校正与动态对比度增强相结合的新方法[J].真空科学与技术学报,2009,29(6):700-703.

[9]MaS,QuanC,ZhuR.AfastandaccurategammacorrectionbasedonFourierspectrumanalysisfordigitalfringeprojectionprofilometry[J].OpticsCommunications,2012,285:533-538.

[10] 师一华,杨金锋.图像处理中改进的Gamma矫正方法[J].安阳工学院学报,2005(6):67-70.

[11] 储 霞,吴效明,黄岳山.照度不均匀图像的自动Gamma灰度校正[J].微计算机信息,2009,25(18):292-293.

[12] 许 龙,李晨钊,李 鹏.弱辐射特征遥感影像的自动伽马校正[J].海洋测绘,2013,33(1):32-34.

[13] 杨金锋,杨国庆,吴仁彪.减少光照影响的自适应Gamma矫正方法[J].信号处理,2005,21(4A):261-264.

[14] 杨金锋,师一华,熊兴隆.光照处理中改进的Gamma矫正方法[J].中国民航学院学报,2006,24(4):39-42.

Gamma Correction Based on Different Brightness Regional Features for Images

DING Yi，LI Yu-hui，LI Bo

(Faculty of Information Engineering and Automation,Kunming University of Science and Technology, Kunming 650500,China)

Uneven brightness can reduce greatly the correctness of image segmentation in image processing.In order to effectively weaken the influence on the image segmentation which brought by uneven brightness,in this paper,a variety of methods of Gamma correction and improved ones are compared and analyzed.In view of the bad effect on correcting image highlights district by using the existing Gamma correction methods,the class cotangent Gamma correction function and elliptical nonlinear correction model are proposed.The experiment shows that on the basis of maintaining the effect on luminance processing in the shadow area and the transition zone by the existing Gamma correction methods,this method narrows the pixel value range of the image highlights area,enhances the correction effect of the image highlights area,and reduces the proportion of the whole image brightness effectively,which makes the brightness distribution more uniform to some extent.In dealing with a larger brightness proportion of image,this method,with good universality,can balance brightness distribution of the image well and greatly improve the segmentation correctness and accuracy of image in some special situations.

image processing;classing cotangent Gamma correction function;elliptical nonlinear correction model;uneven brightness;image segmentation

2015-09-13

2015-12-22

时间：2016-05-25

国家自然科学基金资助项目(61363043)

丁 毅(1991-)，男，硕士研究生，研究方向为图像处理与智能计算。

http://www.cnki.net/kcms/detail/61.1450.TP.20160525.1706.040.html

TP391.41

A

1673-629X(2016)06-0037-03

10.3969/j.issn.1673-629X.2016.06.008