一种前向安全数字签名方案的分析及改进
李顺波,黄光球,彭家龙
(1.西安建筑科技大学 管理学院,陕西 西安 710055;2.西安建筑科技大学 理学院,陕西 西安 710055)
一种前向安全数字签名方案的分析及改进
李顺波1,2,黄光球1,彭家龙2
(1.西安建筑科技大学 管理学院,陕西 西安 710055;2.西安建筑科技大学 理学院,陕西 西安 710055)
前向安全在实际应用中能有效减少私钥泄露对过去时间段签名带来的损失,但会影响未来时段签名的安全性。针对未来时间段的私钥泄露问题,提出了一种强前向安全的数字签名方案。先是对刘亚丽(2010)等提出的基于模m的n方根难题的ElGamal前向安全数字签名方案进行了分析,发现该方案并不能保证未来时间段签名的安全性,即不具备后向安全。于是借助单向散列链技术对该方案的私钥更新和签名算法进行了有效改进,在刘亚丽所提方案的基础上构造了一种基于ElGamal体制的数字签名方案,并对该方案进行了分析。分析结果表明,新方案是正确有效的,同时具有前向安全性和后向安全性。
前向安全;后向安全;数字签名;ElGamal;单向散列链
0 引 言
数字签名是公钥加密技术和数字摘要技术的应用,是保证数据机密性、完整性、真实性、不可否认性的有效手段,已广泛应用于电子商务、金融等领域。根据Kerckhof假设密码算法是公开的,其安全性完全依赖于私钥的安全性。一旦私钥被泄露,不仅当前的数字签名安全性受到威胁,而且过去时段签名的安全性也不能保证,势必导致原来签署的所有签名都作废。针对这个问题,Anderson[1]于1997年首次提出前向安全签名(Forword-secure signature)的思想,即当前私钥的暴露不会影响过去签名的安全性。1999年,Bellare和Miner[2]具体给出了前向安全签名的正式定义,并构造了一种前向安全签名方案。2001年,Burmester等[3]提出了强前向安全的概念,即同时保证前向安全和后向安全。随着电子商务和网络的发展,前向安全已成为信息安全领域的研究热点,提出了基于属性的前向安全[4]、基于双线性对的前向安全[5]、基于格的前向安全[6]、强前向安全[7-10]、前向安全代理[11]等数字签名方案。
2003年,吴克力等[12]给出了基于ElGamal体制的前向安全数字签名方案。接着夏峰等[13]指出吴克力提出的方案并不具备前向安全性,并提出了一种新的基于ElGamal体制的前向安全签名方案,可以将当前私钥隐藏在签名中,确保签名具有前向安全性。2009年,郭远等[14]改进初始参数和私钥更新算法,设计了一种基于ElGamal体制的前向安全签名方案,但该方案无法保证其后向安全性。随后廖小平[15]引入单向散列链对郭远的方案进行了改进,给出的方案既是前向安全又是后向安全的。2010年,刘亚丽等[16]构造了新的密钥生成算法,利用离散对数和合数模平方根困难问题,提出了一种基于ElGamal的前向安全签名方案,该方案具有前向安全性且优于夏峰的签名方案。
前向安全签名在当前私钥泄露时不会对过去时间段的签名造成危害,而后向安全能保证当前私钥的泄露不会对未来时段的私钥造成影响,即不必每次检测出私钥泄露就撤销当前的私钥系统而重建新的密钥系统。通过分析刘亚丽提出的方案,发现其无法保证后向安全性,文中借助单向散列链技术,改进方案的私钥进化和签名算法,给出了基于ElGamal体制的强前向安全数字签名方案。该方案可在满足前向安全性的基础上获得后向安全性。
1 前向安全数字签名
前向安全的基本思想是如果用户当前时间段的私钥泄露了,攻击者虽然可以伪造此时段后的签名,但无法伪造过去时间段的签名;其本质是将签名私钥泄露所带来的影响和损失尽可能减少到最小。前向安全数字签名方案主要由四部分组成:公钥和初始私钥生成、私钥更新、签名算法、验证算法。其关键是签名私钥的更新和签名算法。
用户先注册得到公钥PK和相应的初始私钥SK0,将私钥的有效期分成T个时段,分别记为1,2,…,T。在有效时段内,公钥PK是固定不变的,私钥随着时段的变化进行更新,记i时段的私钥为SKi,更新公式为SKi=h(SKi-1),h是一个单向函数,求出SKi后立即删除SKi-1。这样当攻击者在i时段截获私钥SKi,但无法获得前时段的私钥SKi-1,SKi-2,…,SK0,因此前向的私钥是安全的,称之为前向安全,其私钥更新过程如图1所示。
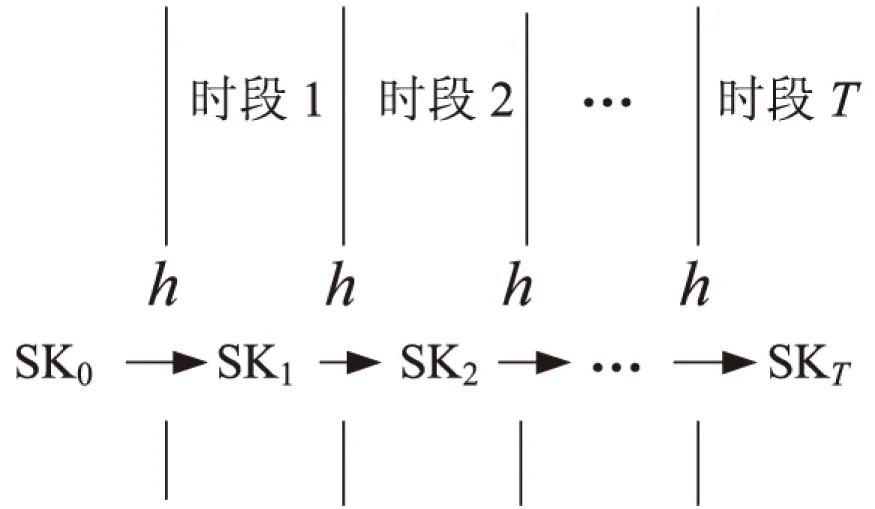
图1 前向安全数字签名的私钥更新过程
2 刘亚丽方案及其安全性分析
2.1 刘亚丽的签名方案
(1)初始参数。

(2)私钥更新算法。
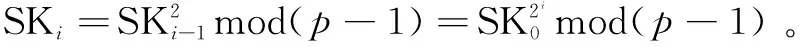
(3)签名算法。
①选择随机数k∈Zp,计算r=gkmodp;
②选择随机数μ∈Zp,计算ω=SKigμmodp;
③计算δ=(H(m)+2T-iμr)k-1mod(p-1),其中m为签名消息;
④发送签名(i,r,ω,δ)给验证方。
(4)验证算法。
如果(PKω-2T-i)rrδ=gH(m)modp为真,则认为签名有效;否则,认为无效。
2.2 刘亚丽方案的安全性分析
(1)刘亚丽方案基于求合数模平方根和离散对数困难问题,将当前时段签名密钥隐藏且仅使用密钥有关信息进行签名,从而无法获得过去时段的私钥和签名,具有前向安全性和抗伪造性。
(2)方案不具备后向安全性。
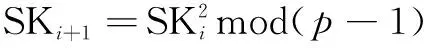
①签名方选择随机数k',计算r'=gk'modp;
②签名方选择随机数μ',计算ω'=SKi+3gμ'modp;
③计算δ'=(H(m)+2T-i-3μ'r')k'-1mod(p-1),则用户对消息m在i+3时段的签名为(i+3,r',ω',δ'),并发给验证方;
④验证方利用签名方的公钥PK,验证下面等式是否成立:
(PKω'-2T-i-3)r'(r')δ'=gH(m)modp
因为:
(gk')(H(m)+2T-i-3μ'r')k'-1=
(g-2T-i-3μ')r'g(H(m)+2T-i-3μ'r')=gH(m)modp
所以攻击成功,即攻击者获得i时段的私钥SKi后,可以伪造出i时段以后的所有签名并通过验证算法,即该方案不满足后向安全性。
3 基于ElGamal体制的强前向安全数字签名方案
新方案将借助单向散列链技术,改进初始参数、签名算法和验证算法。使得构造的方案既有前向安全性,又有后向安全性,即强前向安全的,从整体上有效地提高了数字签名的安全性。
3.1 单向散列链
单向散列函数h(又称哈希函数、杂凑函数)是将任意长度的消息x映射成一个固定长度的函数。满足3个性质:
(1)给定x,容易计算h(x)。
(2)给定h(x),求出x在计算上是不可行的;称为单向性。
(3)找到两个值x和y,且x≠y,使得h(x)=h(y)在计算上是不可行的,称为抗弱碰撞性。
对于随机选取的种子值a(个人密码),用单向散列函数h通过递归散列运算hi(a)=h(hi-1(a))(i=1,2,…,T且h0(a)=a)构造长度为T的一串散列值a,h(a),h2(a),…,hi(a),…,hT-1(a)称为时段T的单向散列链。
令xi=hT-i(a),也就是说xi是散列链中的第T-i个散列值,如表1所示。当攻击者截获第i时段的xi,可由公式xi-1=hT-i+1(a)=h(hT-i(a))=h(xi)容易得到前一时段i-1的xi-1。但当攻击者窃取第i时段的xi时,由于h的单向性,无法用公式xi=h(xi+1)获得后一时段的xi+1。因此表1构造的散列链x1,x2,…,xi,…,xT能保证其后向安全性,为强前向安全的数字签名提供了设计理念。

表1 时段T对应的散列链
3.2 强前向安全签名方案
(1)初始参数。

②选择随机数a,并计算x0=hT(a)。
③公开p,g,x0,T和PK。
(2)私钥更新算法。
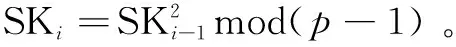
(3)签名算法。
①签名方生成第i时段和i+1时段的散列值xi和xi+1,其中xi=hT-i(a),xi+1=hT-i-1(a)。
②签名方选择随机数μ∈Zp,计算ω=SKigμmodp,ri=gximodp。

④发送(i,ri,ω,δ)给验证方。
(4)验证算法。

(5)安全性分析。
①有效性。
考察验证算法中的等式:
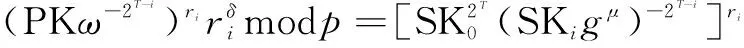
(gxi)modp=
[(gμ)-2T-i]rigH(m)+2T-iμrimodp=gH(m)modp
因此待验证的等式成立,该签名方案正确,且(i,ri,ω,δ)为有效的数字签名方案。
②抗伪造性。
方案采用刘亚丽的方法。当攻击者截获了第i时段的签名(i,ri,ω,δ),由ω=SKigμmodp,若想通过ω得到隐藏的私钥μ是求解离散对数问题,计算上是不可行的。

③前向安全性。
由于签名算法ω=SKigμmodp中有私钥SKi的参与,保证了其签名算法也具有前向安全性。
④后向安全性。
若攻击者截获了第i时段的签名(i,ri,ω,δ),尽管知道了ri=gximodp,但xi,xi+1在单向散列链中且满足xi=h(xi+1),无法由xi得到xi+1。因此攻击者无法获得未来时段的签名,也就是说即使第i时段的密钥泄露,也不会影响此后时段签名的安全性。因此,该方案具有后向安全性。
综上所述,新方案具有不可伪造性、前向安全性和后向安全性;借助单向散列链技术可以有效地提高签名方案的安全性。
4 结束语
前向安全签名方案能有效降低因私钥泄露而造成的损失,但其普遍存在的缺陷就是无法保证私钥泄露后未来时段签名的安全性和及时发现机制。文中借助单向散列链技术,对刘亚丽的前向安全签名方案进行了改进,新方案弥补了其后向安全性,构造了基于ElGamal体制的强前向安全数字签名方案,该方案既具有前向安全性又有后向安全性。
[1]AndersonR.Tworemarksonpublickeycryptology[C]//Thefourthannualconferenceoncomputerandcommunicationssecurity.NewYork:[s.n.],1997:151-160.
[2]BellareM,MinerSK.Aforward-securedigitalsignaturescheme[C]//AdvancesinCryptology-Crypto'99.Berlin:Springer-Verlag,1999:431-448.
[3]BurmesterM,ChrissikopoulosV,KotzanikolaouP,etal.Strongforwardsecurity[M]//Trustedinformation.US:Springer,2001:109-121.
[4] 魏江宏,刘文芬,胡学先.前向安全的密文策略基于属性加密方案[J].通信学报,2014,35(7):38-45.
[5]YuJia,KongFanyu,ChengXiangguo,etal.Oneforward-securesignatureschemeusingbilinearmapsanditsapplications[J].InformationSciences,2014,279:60-76.
[6] 李明祥,安 妮.基于格的前向安全签名方案[J].密码学报,2016,3(3):249-257.
[7] 阿力木江·艾沙,库尔班·吾布力,艾斯卡尔·艾木都拉,等.一种强前向安全数字签名方案[J].计算机工程与应用,2008,44(9):107-108.
[8] 徐光宝,姜东焕,梁向前.一种强前向安全的数字签名方案[J].计算机工程,2013,39(9):167-169.
[9] 廖小平,蔡光兴.一类具有强前向安全性的数字签名方案[J].湖北工业大学学报,2011,26(2):126-130.
[10] 王明伟,胡予濮.一种前向-后向安全的数字签名方案[J].西安电子科技大学学报,2014,41(2):71-78.
[11] 曹 欣,魏仕民,卓泽朋.三个前向安全代理签名方案的安全性分析[J].计算机工程与应用,2015,51(7):98-100.
[12] 吴克力,王庆梅,刘凤玉.一种具有前向安全的数字签名方案[J].计算机工程,2003,29(8):122-123.
[13] 夏 峰,谢冬青,匡华清.一类前向安全数字签名方案的分析与改进[J].计算机工程,2006,32(16):146-147.
[14] 郭 远,徐赐文.基于ElGamal的前向安全签名方案的分析与改进[J].电脑知识与技术,2009,15(6):1459-1460.
[15] 廖小平.前向安全数字签名方案的分析与改进[J].计算机与信息技术,2012,20(1):45-47.
[16] 刘亚丽,秦小麟,殷新春,等.基于模m的n方根的前向安全数字签名方案的分析与改进[J].通信学报,2010,31(6):82-88.
Analysis and Improvement for a Digital Signature Scheme of Forward Security
LI Shun-bo1,2,HUANG Guang-qiu1,PENG Jia-long2
(1.School of Management,Xi’an University of Architecture and Technology,Xi’an 710055,China; 2.School of Science,Xi’an University of Architecture and Technology,Xi’an 710055,China)
Forward security can effectively reduce the damage caused by exposure of the secret key in the past time period,but may affect the signature in the future period.In order to solve this problem,a strong forward-secure signature is proposed.Firstly,Liu Yali’s ElGamal forward-secure signature scheme in 2010 based onnrootofmodulemisanalyzed,andthisschemeisnotbackwardsecurity,whichmeansitcan’tguaranteethesignaturesecurityinthefutureperiod.Then,byusingaone-wayhashchain,thekeyupdatingandsignaturealgorithmisimprovedeffectively.AnewdigitalsignatureschemebasedonElGamalispresentedonthebasisofLiu’sschemeandanalyzed.Theresultshowsthatthenewschemeiscorrectandfeasible,withforwardandbackwardsecurity.
forward-secure;backward-secure;digital signature;ElGamal;one-way hash chain
2015-09-11
2015-12-24
时间:2016-10-24
国家自然科学基金资助项目(11471255,11526161);陕西省自然科学基金(2014JQ1027,2015JQ1014);陕西省教育厅基金(2013JK0589);西安建筑科技大学基金(RC1338,RC1438,JC1321,JC1416)
李顺波(1979-),男,副教授,博士,CCF会员,研究方向为密码学与信息安全。
http://www.cnki.net/kcms/detail/61.1450.TP.20161024.1105.004.html
TP
A
1673-629X(2016)11-0093-04
10.3969/j.issn.1673-629X.2016.11.021

