基于嵌入式移动GPU的离散傅里叶变换并行优化※

曾宝国，杨斌

(1.成都工业职业技术学院，成都 610213； 2.西南交通大学)



基于嵌入式移动GPU的离散傅里叶变换并行优化※

曾宝国1，杨斌2

(1.成都工业职业技术学院，成都 610213； 2.西南交通大学)

摘要:GPGPU能够针对计算密集型的计算问题进行大规模的并行加速，为DFT在嵌入式平台上的高效实现提供了一种新的方式。基于Mali-T604嵌入式GPU实现了针对DFT和FFT的并行加速方案，并进行了实际测试。实验结果证明，所设计的并行方案能够在ARM嵌入式平台上有效加速DFT和FFT，可大大提升移动设备进行数字信号处理的实时性。

关键词:DFT；FFT；GPGPU；Mali-T604 GPU；数字信号处理；ARM嵌入式系统

引言

GPGPU(General purpose GPU)技术近年来在嵌入式领域广泛应用，移动GPU对于输入量庞大的计算密集型、数据可并行化的通用计算问题有显著的加速能力[1]。DFT以及FFT的运算复杂度极高，嵌入式平台上计算能力有限的CPU难以对其进行快速处理。

在实时信号分析场景下，需要高效的计算方案，DFT和FFT的数学模型适合使用GPU对其进行并行加速。本文基于Mali-T604 GPU对DFT和FFT的并行计算方案进行设计，提供了实现方法和实际测试结果，为使用GPGPU技术在嵌入式平台上进行数字信号处理的研究人员提供了参考和借鉴。

1离散傅里叶变换并行化解析

离散傅里叶变换在频谱分析、数字通信、图像处理、遥感遥测等领域有着广泛的应用，有多种算法以不同的时间复杂度对其进行实现，常规的DFT方式和Cooley-Tukey快速变换方式是最常见的两种离散傅里叶变换实现方式。

1.1常规DFT数学模型分析

数字信号处理中应用的离散傅里叶变换通常用于将时域采样信号转换至频域进行分析，其输入数据通常是实数，对于长度为N的实数输入信号序列x[0DK∶N-1]，其一维DFT变换公式为：

(1)

从式(1)可以看出，从实数序列x[0∶N-1]到复数序列X[0∶N-1]的变换过程实际上可转换为矩阵乘法的形式：

(2)

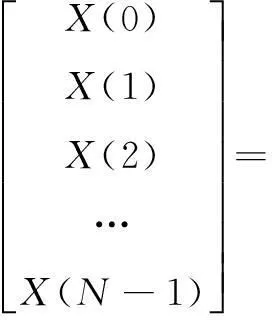
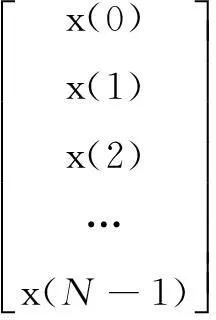
(3)

可见对于输出序列X[0∶N-1]的每个元素而言，其变换过程是相互独立的，其中涉及的是大量的一维向量内积计算，对于数字信号而言，输入序列x[0∶N-1]为实数浮点序列，式(2)和式(3)涵盖的是多次浮点乘法和三角函数计算，嵌入式的CPU(如ARM处理器)对于这样的计算,速度是比较慢的，如果每个元素的变换过程能够独立分解到不同的任务中并行执行,且浮点运算能够快速完成，则常规的DFT就能够快速完成，而MaliGPU正好就是符合这样计算特征的协处理器。

Cooley-Tukey在1965年提出了快速傅里叶变换算法，该算法高效简单，在数字信号处理领域经久不衰，该算法利用了离散傅里叶变换的叠加性质、移位性质和延展性质,简化了DFT变换的运算量，能够得出和常规DFT变换相同的运算结果。

Cooley-TukeyFFT算法可处理长度为2次幂的任意序列的变换，其核心思想是归并，不断利用短序列的变换结果归并产生长序列的变换结果。在计算变换结果X[0∶N-1]的时候，首先分别计算子序列x[0∶N/2-1]和x[N/2,N-1]的变换结果X[0∶N/2-1]和X[N/2∶N-1]，再归并产生X[0∶N-1]。根据原始序列x[0∶N-1]构建序列x1[0∶N-1]={x(0),0,x(1),0,…,x(N/2-1), 0}和序列x2[0∶N-1]= {0,x(N/2),0,x(N/2+1),…,0,x(N-1)}，根据DFT的延展性质和移位性质，有下式成立：

(4)

(5)

(6)

根据DFT变换的叠加性质，有下式成立：

(7)

4个元素的 FFT相对简单，算法从4个元素的变换开始，将原始序列的每4个元素分解为一组，每组元素首先用蝶形运算进行DFT变换，然后利用式(4)～(7)的算法不断归并，得到更大长度的FFT变换结果，直至归并长度等于原始序列长度N为止。

Cooley-Tukey FFT算法的时间复杂度为O(N×log2(N))，相对常规的DFT算法的O(N2)复杂度而言，运算量有所下降，FFT算法中涉及的4元素分组的蝶形运算可以独立进行，互不干扰，后期每个子段的归并过程也是互不依赖的，涉及的也多为浮点乘法运算，适合使用Mali GPU进行性能优化。

2Mali GPU并行计算模型简介

Mali-T600系列的GPU可以支持OpenCL 1.1 Full Profile标准，OpenCL是真正意义上的跨平台异构并行框架，能够真正挖掘出Mali GPU的并行计算特性。在OpenCL框架下，设计者可将预定数目的计算任务下载至Mali GPU端，以多线程形式实现全局的任务并行，其运行过程略——编者注。

OpenCL通过主程序来定义上下文，并管理内核程序在GPU设备的执行[2]，应用程序通过host 提交命令, 驱动设备上的PE 执行内核程序[3]。GPU可以同时处理成百上千的线程，大量晶体管用于ALU[4]，每个Mali-T604 GPU的着色器核心最多可以同时容纳256个线程[5]。在单个线程内部，可以利用Mali GPU内置的128位寄存器和ALU实现向量数据的SIMD(Single Instruction Multiple Data)局部并行加速，Mali-T604 GPU的4个着色器核心以及其中的2条向量运算流水线和1条向量读写流水线能够高效完成128位向量的读写和运算。

3并行DFT以及并行FFT变换实现

传统的DFT以及Cooley-Tukey FFT算法均适合使用Mali GPU进行并行优化，下文分别针对这两种算法介绍并行化的方法。

3.1常规DFT算法并行化实现

常规的DFT算法中，变换结果X[0∶N-1]中的每个元素都是由一维向量的内积得到的，因此每一个元素的计算过程可以分解到单个线程中完成，对于实数序列的DFT变换而言，X(0)和X(N/2)的虚数部分始终为0，对于其他的元素而言，X[k]和X[N-k]具有共轭复数关系，所以真正的计算中只需要计算X[0∶N/2]。因此GPU端总共分配N/2+1个线程，每个元素完成一次长度为N的一维向量的内积，得出X[0∶N/2]中的一个标量计算结果，图1显示了单个线程的运行流程。

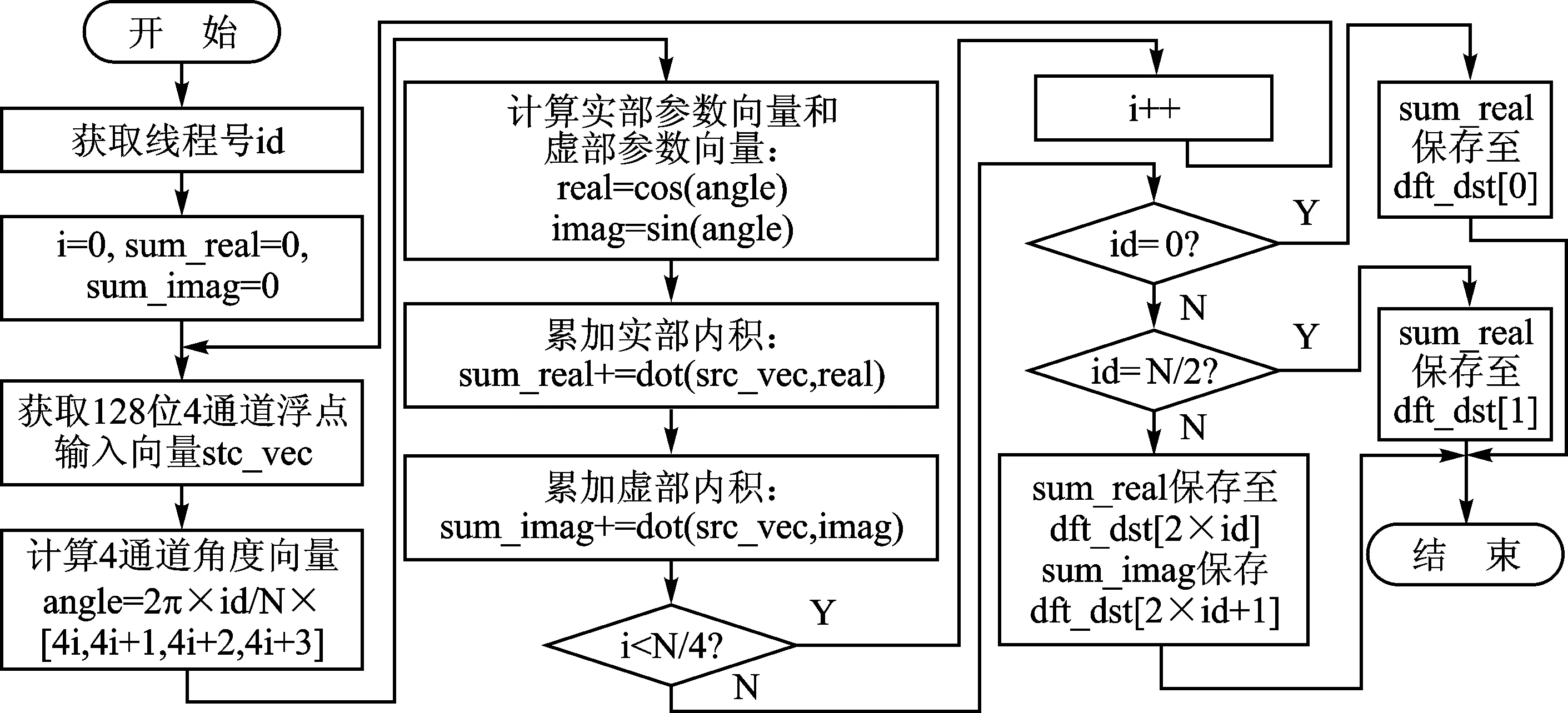
图1　并行DFT变换运算核流程图

OpenCL实现的并行DFT内核源码如下所示：

__kernel void dft(__global float *dft_src,

//变换之前的原始数据缓存，长度为N

__global float *dft_dst, //变换结果的缓存，长度为N

const int N //dft变换的长度){

……

thread_id = get_global_id(0); two_pai_kN = 2.0f*PI*thread_id/N;

sum_real = sum_imag = 0.0f;

for(i=0; i<(N>>2); i++){

src_vec = vload4(i, dft_src); //读取输入向量

angle = (float4)(two_pai_kN) * (float4)( (i<<2)+0, (i<<2)+1, (i<<2)+2, (i<<2)+3);

real = cos(angle); imag = sin(angle);

sum_real += dot(real, src_vec); sum_imag -= dot(imag, src_vec);

}

……

}

3.2Cooley-Tukey FFT算法并行优化实现

Cooley-Tukey FFT算法分为前后两部分，前半部分每4个元素一组,利用蝶形运算进行FFT变换，4个元素进行蝶形运算的方式如图2所示。

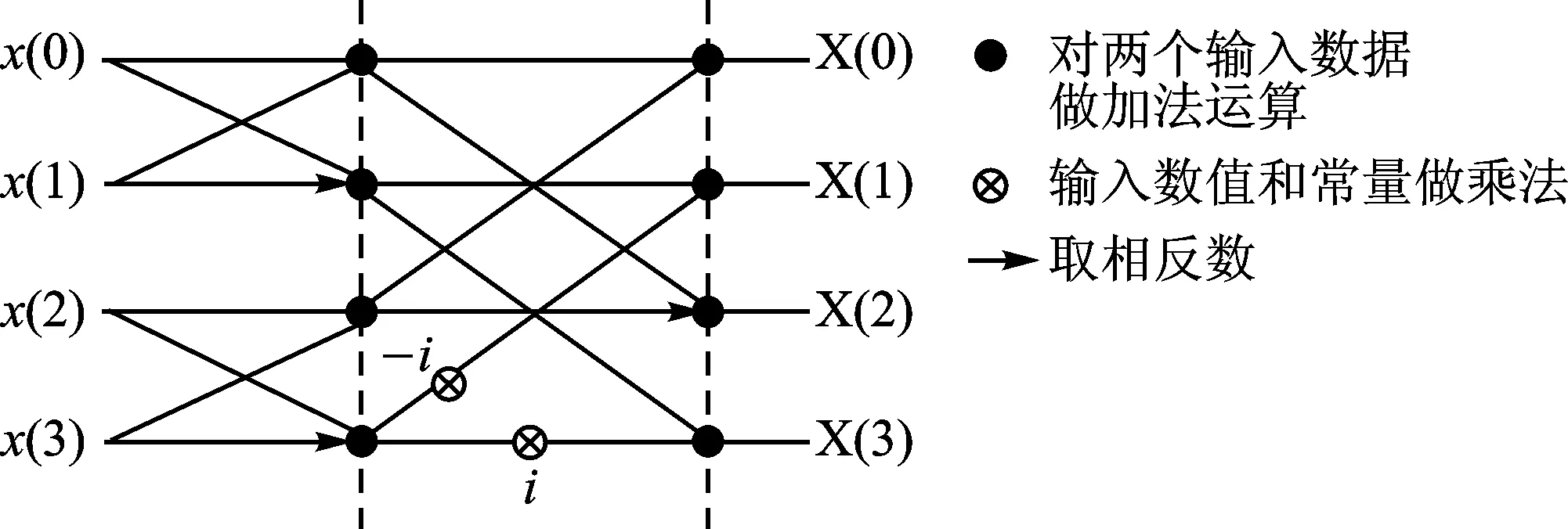
图2　4个元素的FFT蝶形运算

在FFT算法中，一开始每4个元素的FFT变换是相互独立的，因此分配N/4个线程对每一组数据进行图2所示的蝶形运算，图2中的X(0)～X(3)需要从原始数据缓存中读取，其读取位置和分组的组号相关，设线程i(i=0,1,2,…,N/4-1)处理第i组数据中的4个元素，则线程i读取的4个元素的下标应该分别是4i、4i+1、4i+2、4i+3四个数字进行位翻转之后的结果。设log2(N)=b，则下标index位翻转的结果应该是其二进制第(b-1)位和第0位交换、第(b-2)位和第1位交换……直至较高数位和较低数位全部交换一遍之后的结果，能够用Mali GPU进行位运算在每个线程中并行执行，这样能够保证最终归并后的结果是顺序排列的。图2中蝶形运算的输入量都是实数，其计算过程可以拆分成实数部分和虚数部分分别进行，并且都能够用Mali GPU中的4通道浮点向量高效完成，代码如下：

__kernel void fft4(__global float *fft_src,

//变换之前的原始数据缓存，长度是N

__global float *fft_dst_real,

//变换结果的缓存，长度为N(保存实部)

__global float *fft_dst_imag,

//变换结果的缓存，长度为N(保存虚部)

const int bits

//bits=log2(N),用于位翻转计算

){

int id = get_global_id(0);

……//位翻转部分省略

X_real = (float4)(x0);X_real += (float4)(x1, 0-x1, x1, 0-x1);

X_real += (float4)(x2, 0, 0-x2, 0);X_real += (float4)(x3, 0, 0-x3, 0);

X_imag = (float4)(0.0f, x3-x2, 0.0f, x2-x3);

vstore4(X_real, id, fft_dst_real);vstore4(X_imag, id, fft_dst_imag); //回存结果

}

Cooley-Tukey FFT算法的后半部分需要对前半部分的计算结果进行归并，对于长度为N(N为2的幂)的FFT变换，在进行了4元素分组的FFT蝶形运算后，还需进行log2N-2次归并，第i次(i从1开始)归并过程的归并长度为2i+2，即将相邻的两个长度为2i+1的FFT变换序列归并为长度为2i+2的序列。对式(4)～(7)进行分析可知，虽然每次归并的长度翻倍后归并的分组会减少，但总计算量是不变的，因此，将长度为N的浮点复数序列每4个相邻元素分成一组，则不论在第几次归并过程中，必然能够让每组数据两两配对，且分别属于归并运算的两个输入子段，这样每个线程可分别读取这两个长度为4的子段，进行式(4)～(7)的归并计算，并可将实部和虚部的计算拆开，4个浮点数刚好可以凑齐128位,用Mali GPU的向量运算进行处理，综上所述，每一次归并过程可以分配N/8个线程，每个线程进行长度为4的子段的归并计算。

设Mali GPU端编号为i(i=0,1,2,…,N/8)的线程在参与归并长度为merge_len的归并过程中，上一次归并的结果为X_old[0DK∶N-1]，则线程i应首先读取X_old中的第一个长度为4的子段vec0，其偏移地址为：

offset0=(i/(merge_len>>3))×merge_len

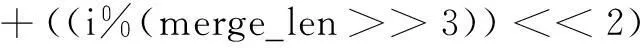
(8)

后一个子段vec1和vec0间的地址间隔是由归并长度决定的：

(9)

根据前文分析，由vec0和vec1两个向量可以计算出新序列X_new[0DK∶N-1]中的两个长度为4的新子段X_new[offset0∶offset0+3]和X_new[of]fset1∶offset1+3]，下面是OpenCL归并内核的核心代码略——编者注。

由于Cooley-Tukey FFT算法中每次归并都依赖于上一次归并的结果，因此在ARM CPU主机端需要将归并内核顺序log2N次加入Mali GPU在OpenCL框架下的命令队列中，并且每次传入的归并长度参数merge_len翻倍。

4优化效果测试

笔者在Arndale Board开发板(核心为ARM Cortex-A15双核CPU+Mali-T604 GPU的Exynos5250 SoC)上和嵌入式Linux操作系统上，对所述的并行DFT和并行FFT优化方案进行了测试，对比ARM Cortex-A15 CPU进行的串行方案和Mali GPU进行的并行方案，以不同长度的随机浮点实数序列进行离散傅里叶变换效率测试，得到的测试数据如表1所列。

表1　离散傅里叶变换并行优化效果对比

从表1的测试数据可以看出，在离散傅里叶变换的变换长度较短的时候，Mali GPU端的运算线程数量不足，其并行运算能力未能发挥出来，故并行方案的计算效率不及串行方案。随着变换长度的增加，Mali GPU端的并发线程数量上升，并行方案的计算效率迅速上升，不论是常规DFT算法还是Cooley-Tukey FFT算法的并行方案,效率都远超串行方案，加速比达到了百倍以上，证明所设计的并行方案的加速效果稳定而有效。对比并行的DFT方案和并行的FFT方案，在变换长度较低的时候，DFT方案的效率更高，虽然FFT方案的总计算量低于常规的DFT算法，但是在归并过程需要多次将归并内核入队，带来了内核运行之间的同步开销。在并发线程不足的情况下，并行化带来的收益未能弥补同步开销，所以并行FFT方案的性能提升不高，在变换长度较大的场景下，Mali GPU端的运算并行度增加，同步开销成为影响效率的次要因素，FFT算法的低运算量特征体现出其优势，使得后期并行FFT方案的效率远超并行DFT方案。在实际工程中，应针对不同的嵌入式GPU硬件结构和变换长度，综合选取两者中效率更高的方案投入具体的应用场景中。

结语

本文基于Mali-T604 GPU设计了针对常规DFT算法和Cooley-Tukey FFT算法的并行优化方案，并在嵌入式Linux操作系统和OpenCL框架下进行了实现。实际测试效果表明，该优化方案效果明显，嵌入式GPU的新兴GPGPU技术在数字信号处理领域有着广阔的应用前景。

参考文献

[1] 龚若皓,杨斌.基于移动多核GPU的并行二维DCT变换实现方法[J] .成都信息工程学院学报,2015,30(1):22-26.

[2] 向阳霞,张惠民,王自强.面向OpenCL模型的DCT并行化[J] .电脑知识与技术,2013,9(26):6007-6011.

[3] 陈钢,吴百锋.面向OpenCL模型的GPU性能优化[J] .计算机辅助设计与图形学学报,2011,23(4):571-580.

[4] Owens J D,Houston M,Luebke D,et al.GPUComputing[J] .Proceedings of the IEEE,2008,96(5):879-899.

[5] ARM Company.ARM Mali-T600 Series GPU OpenCL Developer Guide Version 2.0，2012.

曾宝国(副教授)，主要研究方向为嵌入式应用开发；杨斌(教授)，主要研究方向为嵌入式系统应用及异构并行计算。

(责任编辑：薛士然收修改稿日期：2015-08-27)

Parallelization of DFT Based on Embedded Mobile GPU※

Zeng Baoguo1,Yang Bin2

(1.College of Chengdu Industrial Vocational Technical,Chengdu 610213;2.Southwest Jiaotong University)

Abstract：GPGPU can provide efficient parallel computing solution for the complex compute-intensive computing problem,which is a new way of the efficient implementation of DFT in the embedded platform.In the paper,the parallelization solution of DFT and FFT based on Mali-T604 GPU is proposed.The results of experiment show that the parallel scheme can effectively accelerate DFT and FFT on ARM embedded platform,which can greatly improve the real-time performance of digital signal processing.

Key words:DFT;FFT;GPGPU;Mali-T604 GPU;digital signal processing;ARM Embedded System

中图分类号:TP311

文献标识码:A