一种基于重要性评估的河网分级方法
高 翔,徐 柱
(西南交通大学遥感信息工程系,四川 成都 611756)
An Improved Stream Classification Algorithm Based on Reach Importance
GAO Xiang,XU Zhu
一种基于重要性评估的河网分级方法
高翔,徐柱
(西南交通大学遥感信息工程系,四川 成都 611756)
An Improved Stream Classification Algorithm Based on Reach Importance
GAO Xiang,XU Zhu
摘要:提出了一种改进的河网分级方法,该方法首先对河段的重要性程度进行评估,并利用树结构实现河网的拓扑关系;之后基于河段重要性指数筛选河网主干,并利用主干抽离算法对河网进行逐层遍历;最后基于遍历结果完成河网地层次划分。试验表明,新方法在算法性能和分级结果上均优于传统方法,因此,新方法能够更好地应用于实际的河网分级工作中。
关键词:河网分级;树结构;重要性指数;主干抽离法
地形中的河流具有主干和支流之分,主干与支流的拓扑关系构成了河网的层次结构。为获得这一层次结构,需进行河网分级。目前,河网分级方法主要包括两类:基于分形的分级方法与基于图论的分级方法[1]。基于分形的方法认为河网主干由支流构成,而支流则由亚支流构成,依此类推,最为常用的Strahler法[2-3]、Shreve法[4]、Pfafstetter法[5-6]及Garbrecht法[7-8]都属于该类方法。基于分形的方法的优点在于易于与地理学中有关流域的研究理论相结合,缺点在于难以用简单的数据结构将河网表现出来。而基于图论的方法解决了这一难题,该方法将河段看作节点,将河段的拓扑关系看作节点的连接边,从而利用图表达河网结构。由于图能够充分表现河网的层次关系且便于计算机实现,因此,常用基于图论的方法进行河网地层次划分[9-11]。
众多学者对基于图论的河网分级方法进行了研究。文献[12]通过计算河段流向判断河网的主干与支流;文献[13]利用图论思想设计了树状河系结构化绘制方案;文献[14]通过为河网自动构建河系树完成了河网地层次划分;文献[15]将河网抽象为二叉树,并基于其拓扑结构进行了河网地分级编码;文献[16]通过递归遍历算法对实测河网进行了分级处理。然而,这些方法仍存在一定缺陷,具体表现为:①确定河段层次的方法不合理,不能准确地划分河网的主干与支流;②所采用的河网遍历方法均未充分发挥树结构特有的优势。鉴于此,本文提出一种基于重要性评估的河网分级方案。该方法通过计算河段的重要性指数来确定上下游河段的层次关系;同时,为充分发挥树的结构优势,利用主干抽离法完成河网的遍历及河段层次的划分。试验表明,与传统的分级方法相比,新方法能够更加准确地提取河网的主干与支流,从而清晰地表达河网的层次结构。
一、河段重要性指数计算
目前,判断河网上下游河段层次关系的方法主要有两种:长度优先法与角度逼近法[17]。长度优先法在判断河段层次关系时,首先获取河流交汇处的上游河段,然后计算所有上游河段的几何长度,最后,选取最长的河段作为同级主干,进行新一轮河段层次的判断。角度逼近法在判别河段层次时,依次计算上下游河段间的夹角,选取夹角最接近于180°的河段作为同等级的主干河段。
长度优先法与角度逼近法利用几何形态对上下游河段的层次性进行判断。然而,当河网中存在大量较短的河段时,该类方法并不能准确地判别出河网的主干与支流。如图1(a)所示,河流主干河道由1号河段流入2号河段,最终汇入4号主河道,因此,当前局部河网的主干为1—2—4。当采用长度优先法进行河段层次判别时,由于3号支流河段长度大于2号河段,因此,3号被错误地判别为与4号河段同级的主干河段,从而导致主干提取不准确。对于角度逼近方法,也存在类似问题。如图1(b)所示,3号河段位于下游,1号与2号河段位于上游,当遍历到3号河段时,分别计算3号与1号、3号与2号河段的夹角,由于2号与3号河段的夹角更加接近于180°,因此,最终将2号错误地判定为与3号河段同级的主干河段。

图1 基于几何形态的河段分级方法
长度优先法与角度逼近法之所以无法准确提取河流主干与支流,是因为该类方法的河网分级结果完全依赖于河段的几何形态。从地理学的角度考虑,利用河段的几何形态进行河网等级划分并不合理,因为对于现实地表中的河流主干,其河段的几何长度并不一定大于支流,河段间的夹角也并不一定逼近180°。
从分形的角度分析河网结构可以发现:河网的亚支流汇聚,形成支流,支流汇聚,形成河网主干,这表明层次越高,河段的汇水能力也应当越强。因此,可以通过量化河段的汇水能力进行河网地层次划分。有学者进行了相关尝试,如文献[1]通过设定汇水量阈值,对河段中的节点进行主干标注,从而辅助完成河网的分级;然而阈值的设定带有较强主观性,且地形不同,其最佳的阈值也不尽相同,因此这一方法并不具有普遍适用性。文献[17]基于河段流量的中点策略进行河段的层次划分,文献[17]则利用河段交汇点处的汇水量确定河段间的层次关系。然而,这些方法(后文称之为单节点流量评估法)仍存在不足:①河段变化复杂,选点策略不同,计算得到的河段等级也不尽相同,这使得河网分级结果存在较强的不确定性;②无论使用何种选点策略,河段中的单点始终无法对河段总体的平均汇水能力进行准确评估。因此,利用该类方法计算得到的河网层次的准确性还有待商榷。
要保证河网分级的准确性,必须采用一种更为合理的、普遍适用的方法。考虑到河网分级过程实则是一个评估河段重要性的过程,因此,只要选择恰当的方式进行河段的重要性评估,即可准确地划分河网的层次结构。要对河段的重要性进行评估,首先考虑到的方案是统计河段的汇水总量,因为河段的汇水总量是其汇水能力最直观的表达。然而,利用汇水总量进行河网分级仍存在缺陷,这一缺陷与长度优先算法存在的缺陷类似。如图1(a)所示,2号与4号河段为同级主干,3号河段为主干支流,因此,2号河段的重要性程度强于3号;然而,由于2号河段长度较小,途径的汇水量栅格总数也相应较少,这使得2号河段的汇水总量小于3号。可以发现,汇水总量仍无法用于准确评估河段的重要性。之所以存在这一问题,是因为汇水总量的计算受河段几何长度的约束,而用于衡量河段重要性的指标应当与几何长度无关。因此,应当将所求得的汇水总量平均分配到河段的单位长度中,最终河段重要性指数为
(1)
式中,I为河段的重要性指数;Ai为第i个栅格的汇水量;N为当前河段途径的所有累积量栅格的总数;L为当前河段的几何长度。图2进一步说明了基于重要性指数的河网分级过程,图2(a)为当前区域的栅格流向,图2(b)为基于流向计算出的汇水累积量,图2(c)为统计得到的河段重要性指数,图2(d)为基于重要性指数获得的河网层次,其主干为1—2—5—9,二级主干为4—7、3及8,三级主干为6。
二、构建河网树
1. 河网的树形结构
河网中的上下游相互连接,通常出水口处河段的入度大于零,而出度为零,河流源头处的入度为零,出度大于零,介于源头与出水口河段的入度与出度均大于零,且彼此连接,这很好地符合了图的拓扑结构,因此,常用图来表达河网中河段的拓扑关系。河网中图的拓扑关系可以用树结构实现,其中河网中的河段用树的节点表示,上下游河段的连接关系用树的边表示。出水口河段与多条上游河段相连,且不与任何下游河段相连,因此,将出水口作为树的根节点;源头河段与下游河段相连,不与任何上游河段相连,因此,将源头河段作为树的叶子结点。树中节点包含三类属性:节点的编号、孩子节点的编号,以及节点的重要性指数。利用树表达河网的拓扑结构,能够清晰地表达河网中河段的层次关系,如图3所示,1号河段位于出水口位置,因此作为树的根节点,16—31为源口河段,因此作为树的叶子节点。
2. 利用树进行河网层次划分
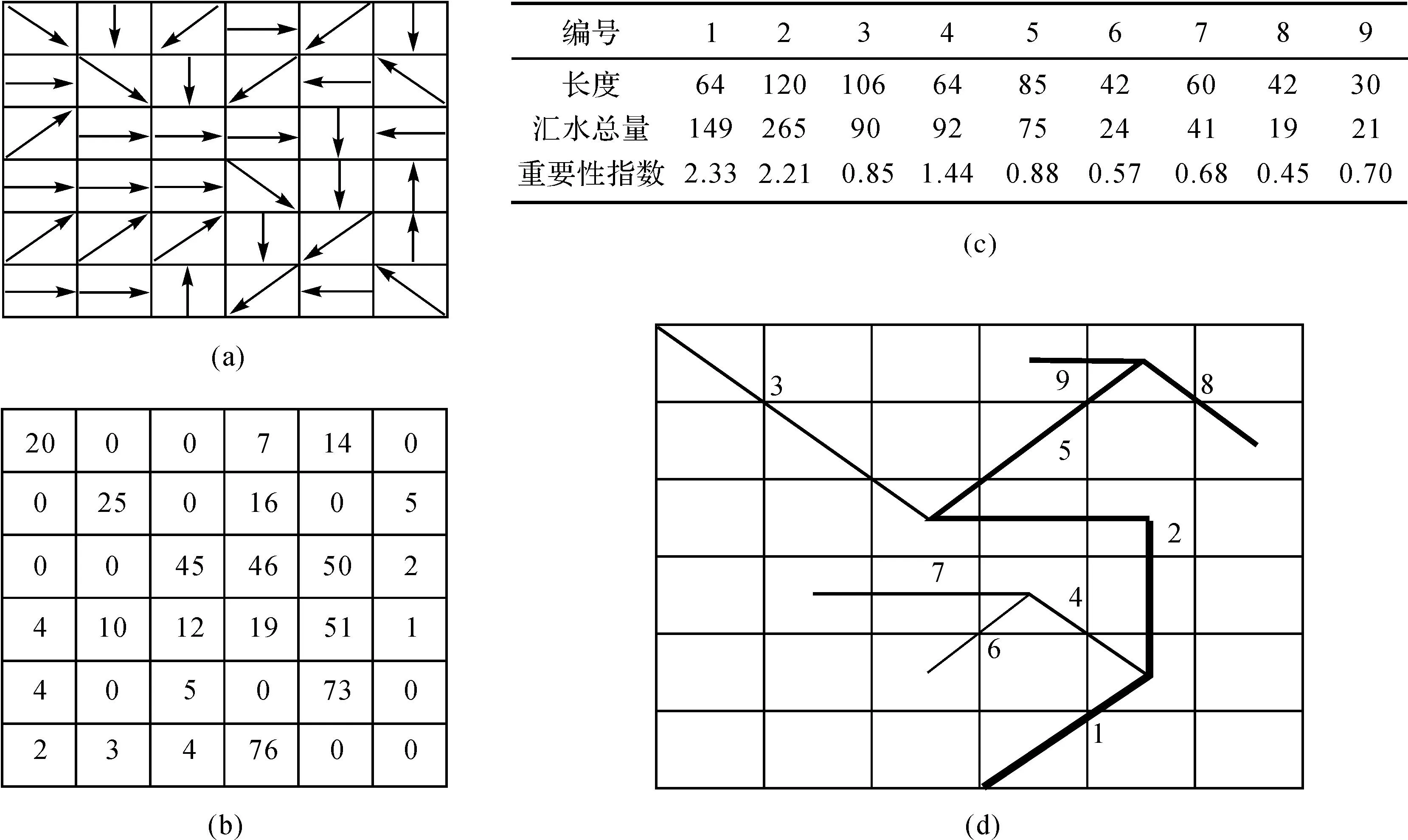
图2 重要性指数地计算

图3 河网的树形结构
有学者利用树结构进行河网层次的划分[13-14],然而均采用对已遍历河段进行标注的方式辅助完成分级过程,这一方法不仅需要额外开辟存储空间,还会导致已遍历节点的多次重复访问,从而使得遍历效率低下。为充分发挥树结构的优势,本文采用主干抽离法进行河网层次的划分。该方法首先定位到树的根节点位置;接着,从根节点处向下遍历,逐一比较孩子节点的重要性指数,将最为重要的孩子节点筛选出来;当遍历到叶子节点时,将一次遍历经过的所有节点从当前树中抽离出来;抽离主干后,原有树自动分解为一系列子树,对子树重复上述过程,直到所有子树仅包含一个节点为止。利用主干抽离法进行河网分级,无须对已遍历河段进行额外标注,且随着主干的移除,树中的节点急剧减少,子树的遍历效率也得到了提升。值得注意的是,由于树节点仅保存了自身与孩子节点的拓扑关系,不包含与父节点的拓扑关系,因此,当从树中移除已遍历的河网主干时,生成的新树无须重组。可见,主干抽离法能够最大限度地发挥树结构的优势。图4对主干抽离过程进行了阐述。起初,当前河网包含31个节点,通过重要性比对,筛选出第1等级的河网主干:1—3—6—12—25;将主干从树中抽离,原树自动分解为4棵子树,共包含26个节点,对这4棵子树进行新一轮分级运算,筛选出第2等级的主干:2—5—10—21、24、13—26和7—14—29;对次级主干进行抽离,得到6棵子树,共包含16个节点,对其进行新一轮遍历,得到第3等级的主干:4—9—18、20、11—23、27、28和15—30;继续抽离主干,得到7棵子树,共包含9个节点,对其进行分级遍历,得到第4等级主干;最终,仅剩叶子节点16,将其分为第5等级主干。至此,完成所有河段的分级过程。

图4 基于主干抽离算法的河网遍历过程
三、试验与对比
1. 研究区域
本文选取GDEM 30 m分辨率DEM进行试验分析,DEM大小及基本参数见表1。
由表1可知,试验所选DEM高差、平均坡度及表面粗糙度都较大,这表明该区域具有一定的地表复杂度,以此作为试验区域可提取较为丰富的河网。所选DEM如图5(a)所示,提取的等高线(灰色细线)与河网(黑色粗线)如图5(b)所示。

表1 DEM地形基本参数

图5 试验DEM河网提取结果
2. 河网分级对比
本文选用Strahler分级法、Shreve分级法、长度优先分级法、角度逼近分级法、单节点流量评估法及重要性指数评估法进行河网分级对比,各种方法的分级数见表2,分级结果如图6所示。由于Shreve法、长度优先法、角度逼近法级数较多,为便于表达,图例部分仅显示前10层。

表2 不同分级方法下的层次总数

图6 不同方法的河网分级结果
与其他方法相比,Shreve法获得的层次数最多,从图6(b)可以发现,河段间的等级差异较大,无法表达河网的层次结构。与Shreve方法相比,长度优先法和角度逼近法划分的层次数要少得多,然而通过观察图6(c)与图6(d)可以发现,这两种方法划分的河网等级依旧较为破碎,很难从分级结果中提取河网的主干与支流。这两种较为经典的分级方法之所以不能够很好地划分河网的层次,是因为所选用的地区表面粗糙度大,地形复杂,提取的河网存在大量的短小河段,这同时表明,长度优先与角度逼近策略无法用于对复杂地形进行河网层次划分。Strahler法依据河段的连接关系划分河网等级,所有的末端支流被分为第1等级,同等级的支流汇聚成第2等级,如图6(a)所示。这一方法虽能获得较少的河网等级,但所采用的分级规则使得该方法无法确定河网的主干与支流。与前4种方法相比,单节点评估法划分的河网等级能够更好地表达河网的层次关系,如图6(e)所示,黑色矩形框内标注了局部河网的层次关系,其中,第4等级的河段为当前河网的主干河段,这一主干河段由第5等级的支流汇流而成,同时,第5等级的河段上存在少量第6等级的河段,而第6等级的河段上存在少部分第7等级的河段。可以发现,在局部区域内,基于单节点的方法能够较好地确定河段间的层次,然而,该方法的整体性较差,不能完整地提取河网的主干和支流,这主要是因为该方法采用的划分河段层次的方法仍不够精确,无法保证整体河网层次的准确性。与前5种方法相比,重要性评估法的分层数极少,且划分的河段等级能很好地表达河网的层次结构,如图6(f)所示,其中粗线为当前河网的第1等级主干。由分析可知,当河网变化程度较为丰富时,与其他方法相比,重要性评估法能够更好地提取河网的主干与支流,从而清晰地表达河网的层次结构。
本文采用的方法不仅在河网层次的表达上优于其他方法,在分级运算效率上也同样优于传统方法。在配置为2.9 GHz CPU、16 GB内存、i7处理器的计算机上进行试验,当河段总数达到20 000时,利用循环递归的方式进行河网遍历,总耗时为11 s,利用主干抽离法进行河网遍历,总耗时仅为6.7 s,因此,新方法能够在保证河网层次划分准确性的基础上更加高效地完成分级过程。
四、结束语
为获得河网的层次结构,需对河网进行分级,本文首先通过计算河网的平均汇水量评估河段的重要性程度,并在此基础上建立河网的树形结构;接着基于计算得到的重要性指数,利用主干抽离算法逐层筛选河网的主干;最后基于遍历结果完成河网的层次划分。试验部分分别选用Strahler分级法、Shreve分级法、长度优先分级法、角度逼近分级法、单节点流量评估法,与本文所采用的重要性评估法进行对比分析。试验表明,当地形较为复杂时,Shreve分级法、长度优先分级法、角度逼近分级法获得的分级数过多,无法用于提取河网的主干与支流;Strahler分级法与单节点流量评估法获得的分级数相对较少,但分级结果仍较为破碎,无法清晰地表达河网的层次结构;利用重要性评估法进行河网层次划分,不仅能够获得极少的分级数,还能够清晰地表达河网的层次关系;同时,与传统方法相比,新方法的河网分级算法性能也有较大改善。因此,新方法能够更好地应用于实际的河网分级工作中。
参考文献:
[1]王敏嫱. 基于DEM的水文要素提取及水文拓扑结构建立的研究[D]. 西安:西北大学, 2012.
[2]STRAHLER A N. Hypsometric (Area-altitude) Analysis of Erosional Topography[J]. Bulletin of the Geological Society of America, 1952, 2(63):1117-1142.
[3]陈于林. 基于DEM的水系提取及水系网多级分解[D]. 成都:西南交通大学, 2006.
[4]SHREVE R L. Infinite Topologically Random Channel Networks[J]. The Journal of Geology, 1967, 75(2):178-186.
[5]VERDIN K L, VERDIN J P. A Topological System for Delineation and Codification of the Earth’s River Basins[J]. Journal of Hydrology, 1999, 218(1-2):1-12.
[6]罗翔宇, 贾仰文, 王建华, 等. 基于DEM与实测河网的流域编码方法[J]. 水科学进展,2006,17(2): 259-264.
[7]GARBRECHT J. Determination of the Execution Sequence of Channel Flow for Cascade Routing in a Drainage Network[J]. Hydrosoft, 1988, 1(3):129- 138.
[8]任立良, 刘新仁.数字高程模型在流域水系拓扑结构计算中的应用[J]. 水科学进展, 1999, 10(2):129-134.
[9]陈玉芬, 李书琴,何东健.流域拓扑结构分析与计算机实现[J].干旱地区农业研究,2005, 23(5):183-186.
[10]刘先龙, 杨勤科.流域拓扑关系建立方法研究[J].水土保持研究,2010,17(3):82-86.
[11]毋河海.河系树结构的自动建立[J].武汉测绘科技大学学报,1995,20(S0):7-14.
[12]刘先龙. 基于DEM的流域水文网络建立方法研究[D]. 杨凌:西北农林科技大学, 2011.
[13]张园玉,李霖,金玉平,等.基于图论的树状河系结构化绘制模型研究[J]. 武汉大学学报(信息科学版),2004, 29(6):537-543.
[14]张青年, 全洪. 河系树的建立及其应用[J]. 中山大学学报(自然科学版), 2005, 44(6):299-302.
[15]李铁键, 王光谦, 刘家宏, 等. 数字流域模型的河网编码方法[J]. 水科学进展, 2006, 17(5):658-664.
[16]曾凡华, 胡静涛, 王亚平, 等. 基于实测河网的河流编码算法[J]. 信息与控制, 2010, 39(5):614-620.
[17]黄萌萌. 基于DEM分析的山体对象构建[D]. 成都:西南交通大学, 2014.
引文格式: 高翔,徐柱. 一种基于重要性评估的河网分级方法[J].测绘通报,2016(1):115-120.DOI:10.13474/j.cnki.11-2246.2016.0029.
作者简介:高翔(1989— ),男,硕士生,研究方向为地图制图学与地理信息系统。E-mail:15281063584@163.com
基金项目:教育部“新世纪优秀人才支持计划”(NCET-12-0942);“2011计划”轨道交通安全协同创新中心西南交通大学先行先试项目
收稿日期:2014-10-20
中图分类号:P208
文献标识码:B
文章编号:0494-0911(2016)01-0115-06

