基于对策论的反舰导弹目标捕捉策略研究

沈培志，聂奇刚，张邦钰，李　涵

(1.海军航空工程学院　a.指挥系; b.研究生管理大队, 山东 烟台　264001;

2. 91362部队, 浙江 宁波　315000; 3. 92212部队, 山东 青岛　266000)



基于对策论的反舰导弹目标捕捉策略研究

沈培志1a，聂奇刚1b，张邦钰2，李涵3

(1.海军航空工程学院a.指挥系; b.研究生管理大队, 山东 烟台264001;

2. 91362部队, 浙江 宁波315000; 3. 92212部队, 山东 青岛266000)

摘要：分析了水面舰艇应对反舰导弹的典型机动规避策略，利用蒙特卡洛仿真法计算了水面舰艇进行典型规避策略时反舰导弹的捕捉概率，并以此建立了反舰导弹目标捕捉策略问题的赢得矩阵，计算得到了反舰导弹在应对目标机动时，目标捕捉的最优混合策略。

关键词：反舰导弹；目标捕捉；对策论；最优混合策略

本文引用格式：沈培志，聂奇刚，张邦钰，等.基于对策论的反舰导弹目标捕捉策略研究[J].兵器装备工程学报，2016(1):15-17.

Citation format:SHEN Pei-zhi, NIE Qi-gang, ZHANG Bang-yu,et al.Target-Catching Strategy of Anti-Ship Missile Based On Game Theory [J].Journal of Ordnance Equipment Engineering,2016(1):15-17.

目前，舰艇目标对来袭反舰导弹一般可通过机动规避、有源干扰、无源干扰、舰炮抗击、舰空导弹抗击等多种手段进行应对，因而要想突破水面舰艇层层防御变得越发困难，若只使用同一种类型的反舰导弹突击，将很难能达到射击目的。若使用不同类型的数枚反舰导弹同时进行射击，则会使舰艇目标避免一种或多种抗击手段失效而获得较高的命中概率。因此，对水面舰艇可能采取的措施进行预判，并选择合适的反舰导弹提高命中概率就显得尤为必要。为了使该问题简化，本文主要从目标捕捉的角度，研究在舰艇采取机动规避措施时，为达到较高捕捉概率，多枚反舰导弹的使用策略。对于反舰导弹应对水面舰艇的其他抗击手段同样可以采用类似的方法，限于篇幅本文不再赘述。

1反舰导弹及水面舰艇舰艇策略分析

1.1题设和策略分析

由于目标的机动规避措施主要影响导弹的选择能力，因此根据文献[1]可以假设反舰导弹的类型有3种，分别是A型：对左侧目标捕捉概率较大；B型：对中间目标捕捉概率较大；C型：对右侧目标捕捉概率较大。因此，反舰导弹的策略集为

(1)

其中α1、α2、α3分别为A、B、C三种导弹类型。

水面舰艇进行机动规避时可以采取改变航向及改变航速等策略，这里以8个典型的运动方向为例，假设目标可能采取向东、东南、南、西南等8个方向以最大航速作直线运动的策略，由此可得水面舰艇的策略集为：

(2)

各策略含义为水面舰艇向8个方向运动共8种策略如表1。

表1　舰艇机动策略集

1.2混合策略定义

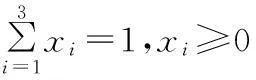
(3)

若反舰导弹按混合策略X=(x1,x2,x3)，即以一定的概率分别取纯策略α1,α2,α3时，反舰导弹的赢得的全数学期望为

(4)

此时，反舰导弹和舰艇目标可以在数学意义上存在最优策略。

2计算赢得矩阵

2.1捕捉概率计算模型

以反舰导弹自控终点散布和目标散布两个参数为基础条件，分别设置一定的雷达搜索范围，利用蒙特卡洛法可以建立导弹目标捕捉概率计算模型如图1所示。

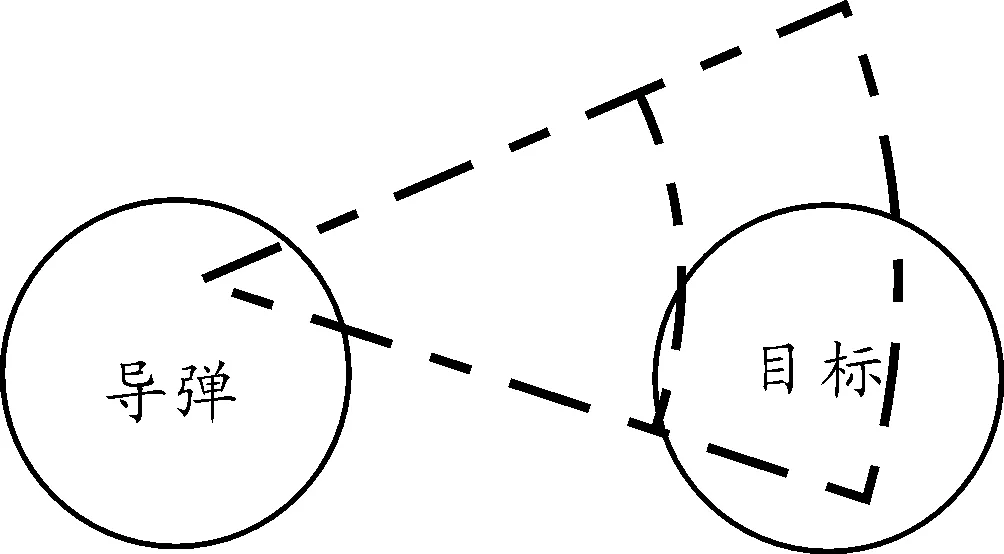
图1　目标捕捉示意图

设目标舰艇距离反舰导弹发射点200 km，导弹和目标散布分别为3 km和1 km。现以末制导雷达搜索范围为变量，其变化范围为：搜索角度为0°～30°，搜索距离为0～10 km。可得目标捕捉概率变化如图2所示。

图2　捕捉概率变化

由图2可知，捕捉概率随搜索范围增大而增大。

2.2计算赢得矩阵

根据上一节的分析可知，选用搜索角度30°以及搜索距离10 km为计算条件时可得最大捕捉概率，因此可计算出不同类型导弹对目标向不同方向机动时的捕捉概率。

设舰艇发现来袭导弹后开始按一定方向机动，至末制导雷达开机时，目标向各方向的机动距离为6 km，可得赢得矩阵如表2所示。

当然，对于不同的初始输入参数，所得的赢得矩阵不同，当存在鞍点时，可以找出该对策的最优纯策略，不存在鞍点时，需要计算最优混合策略。因此下文将根据矩阵是否存在鞍点，重点研究反舰导弹应对目标机动时，提高目标捕捉概率的对策。

表2　赢得矩阵

3计算最优策略

通过分析可知，该赢得矩阵不存在鞍点。使用优超方法对赢得矩阵降阶后可得2×2型矩阵对策如表3所示。

表3　优超简化矩阵

由此，可以通过公式法[3]，设其最优策略为：

(5)

根据最优混合策略有解的充要条件可得[3]：

(6)

(7)

4结论

本文利用对策论的相关方法，分析了水面舰艇采用纯机动规避时，提高反舰导弹捕捉概率的策略。通过举例计算可知，本例的赢得矩阵不存在鞍点，因而要达到双方的期望，必须使用最优混合策略，即反舰导弹应使用A型弹和B型弹约2：1的比例进行搭配。严格地说，无鞍点矩阵对策在混合策略意义下的解更适合用于多次重复对抗，军事决策是一次进行的决策，看似不符合这个前提，但若对多枚导弹进行分配决策时，可以将重复决策问题的次数等效理解为导弹的数量，因而使用对策论对多枚导弹的使用问题进行研究是比较合适的。

参考文献：

[1]王光辉，严建钢，辛旭光.基于选择方式的寻的雷达对编队目标捕捉算法[J].弹箭与制导学报，2010(12).

[2]胡家凤.舰艇无源干扰分层防御反舰导弹攻击的方法[J].飞航导弹，2003(8).

[3]谭乐祖，翟军.军事运筹学教程[M].兵器工业出版社，2010.

[4]巫银花，何常青，宋勇. 基于熵权法的潜射反舰导弹作战效能灰色关联评估方法 [J].兵工自动化，2015(2):40-42.

[5]高晓冬，王光辉，李传顺. 一种改进的反舰导弹前置点射击方式目标捕捉概率算法[J].海军航空工程学院学报，2012(2)：228-230.

(责任编辑周江川)

【装备理论与装备技术】

Target-Catching Strategy of Anti-Ship Missile Based On Game Theory

SHEN Pei-zhi1a, NIE Qi-gang1b, ZHANG Bang-yu2, LI Han3

(1.a.Department of Command; b.Postgraduate Management Department,

Naval Aeronautical and Astronautical University, Yantai 264001, China;

2.The No. 91362ndTroop of PLA, Ningbo 315000, China;

3.The No.92212ndTroop of PLA, Qingdao 266000, China)

Abstract:Typical ship escaping tactics against threaten of anti-ship missile was analyzed. The acquiring probability of anti-ship missile when the surface ship had typical prevention strategy was calculated by Monte-Carlo simulation. The won matrix of target-catching strategy was built by the won function which was based on the acquiring probability. Optimal mixed strategy of anti-ship missile target-catching against ship escaping was obtained.

Key words:anti-ship missile; target-catching; game theory; optimal mixed strategy

文章编号：1006-0707(2016)01-0015-03

中图分类号：E927

文献标识码：A

doi:10.11809/scbgxb2016.01.003

作者简介：沈培志(1972—)，副教授，主要从事海军兵种作战运用研究。

收稿日期：2015-10-21；修回日期：2015-11-09