基于优化UIO的风轴速度传感器故障检测*

文 | 李东亮，文传博

基于优化UIO的风轴速度传感器故障检测*

文 | 李东亮，文传博

随着风电机组装机容量的增大，以及越来越多海上风电机组的安装，对其故障的快速检测和隔离提出了新要求。在大多数工业制造的机组中，只用相当简单的方法检测和隔离故障。

风电机组是将风能转化成电能的装置。在风力的作用下，驱动机组叶片和与之相连的风轴旋转，再通过齿轮箱将旋转速度提升，来促使发电机发电。在风速低于额定风速时，调节发电机转子转速，实现发电机的转速控制，尽可能最大捕获风能；而当风速高于额定风速时，变桨距控制能随风速大小进行自动调节，因而能吸收尽可能多地风能并转化为电能，实现功率的平稳输出。速度传感器作为整个控制系统的重要元件，在测量风轴转速、发电机转速方面发挥着重大作用，因此针对其进行故障诊断尤为重要。

针对风电机组传动系统传感器故障诊断和隔离，已有较多研究。其中大多通过Kalman算法和设计未知输入观测器，来诊断风轴转速传感器、发电机转速传感器和转换器扭矩传感器故障，但针对传感器故障类型描述不够具体。

本文也运用了未知输入观测器的方法，针对风电机组传动系统机理模型，应用未知输入观测器，并通过卡尔曼滤波算法设计反馈矩阵，结合了未知输入观测器与Kalman滤波算法的各自优点，重构解耦了干扰，并达到了降噪的效果，采用极大似然比的方法设定阈值，从而有效地检测出风电机组风轴转速传感器故障。

风电机组传动系统模型

风电机组基准模型如图1所示，传动系统作为机组的重要部分，在转速增速、制动和传递扭矩方面发挥着无可替代的作用。风力带动风电机组的叶片转动产生的机械能，通过传动系统传递给发电机部分，以驱动发电机工作，从而实现能量从叶片传递至发电机部分。

图1中，vw为实际风速，vw,m为实际风速的测量值，βm为实际桨距角测量值，βr为桨距角参考值，ωg为发电机实际转速，ωg,m为发电机转速测量值，ωr为实际风轴转速，ωr,m为风轴转速测量值，Pr为发电机功率参考值，τr为实际空气动力学扭矩，τg为实际转换器部分扭矩，τg,r为转换器部分扭矩参考值。

根据传动系统的动态过程，通过如下微分方程可以表示出来：

其中，θΔ表示传动系统扭矩角，Jr和Jg分别表示低速轴转动惯性和高速轴的转动惯性，Kdt表示抗扭劲度，Bdt表示扭转阻尼系数，Ng表示传动比，ηdt表示传动系统的效率。将上述式子写成状态空间方程的形式为：

由于叶片的扭矩与实际的风速有关，而风速是实变的，不可能精确地测量，因此，在此状态下把这种测量误差看作是未知干扰，那么传动系统的状态方程可写为：

未知输入观测器的优化设计

通过重构并解耦干扰可得未知输入观测器方程为：

其中，F，G，L和H是解耦未知输入、优化观测器所设计的矩阵，并满足以下方程：

通过上述观测器的设计过程可以看出，在不考虑噪声影响的情况下，系统干扰项可以通过干扰重构过程得到补偿，达到干扰解耦的效果，但在实际系统中，噪声往往与干扰并存，为了降低噪声的影响，采用卡尔曼滤波算法进行反馈矩阵 的设计。

根据上述观测器方程（1），系统残差信号可表示为：

所以系统残差信号可表示为：

残差信号的协方差可表示为 ：

为了方便计算，令A1＝A－HCA＝TA，则 残差信号的协方差的更新过程可表示为：

其中，由于R和CP（k）CT都为正定矩阵，故存在矩阵V使得VVT＝CP（k）CT＋R，并令D＝A1P（k）CT（HT）－1，则：

式中，当LV－d＝0时，残差信号协方差矩阵最小，可以得到：

此时，残差信号的协方差最小为：

根据式（4）和式（5）即可计算反馈矩阵L。再结合公式（2）可构造出优化后未知输入观测器，进一步计算得到状态估计值），可以计算出残差信号的幅值。理论上，在无故障时，应该近似为零，而当出现故障时，将会偏离零值。

故障阈值的设计

实际情况下，残差由于受系统建模精度的影响，无故障情况下难于严格为零，因此为了准确有效地检测出故障信息，采用阈值门限的方法进行故障的检测，即当残差信号大于阈值时则系统出现故障报警。考虑到系统本身的噪声带来的随机性，采用极大似然比来对残差信号进行评估，广义似然比的检验统计量定义为：

误报率Pf是指在系统没有发生故障时，检测系统却判定系统有故障发生的概率，阈值Jth的设定根据实际系统要求的误报率满足下式关系：

式中Pf的选择需要权衡低误报率和高检测率，在选定误报率Pf后，通过查找χ2分布表就可以确定阈值Jth，残差信号的阈值评价逻辑为：

仿真分析

针对常见风电机组风轴转速传感器加性和乘性故障，在系统仿真中使用表1所示的故障信号。

在系统无故障时，对比分析了普通未知输入观测器与本文优化的未知输入观测器，如图2所示，从仿真图可以看出，所设计的普通未知输入观测器得到的残差信号在零值附近波动较大，因此在系统无故障发生时，容易产生误报警，而通过Kalman滤波算法设计的优化未知输入观测器增强了系统的鲁棒性，达到了抑制噪声的效果，故其所得残差信号波动较小，相对普通的未知输入观测器更能有效地进行故障检测。

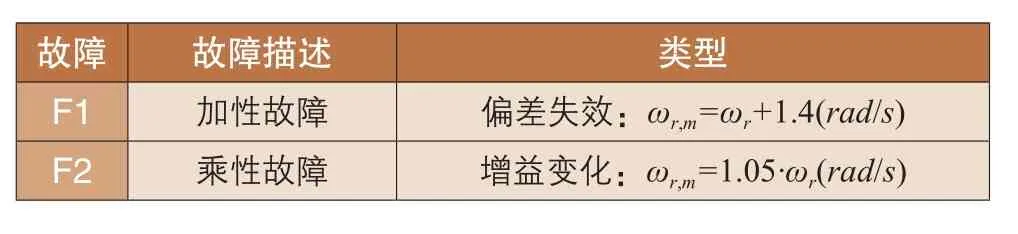
表1 仿真故障信号

通过采用最大似然比对残差信号进行评估，选定误报率Pf＝0.0005，根据χ2分布表得到阈值Jth＝11.047，对表1所示传感器故障进行评估的仿真图如图3所示。

当系统在t＝40s发生加性故障F1时，其仿真图如图3所示。从图中可以看出，在t＝40s，系统产生故障信号，仿真出的残差信号明显比设定的阈值要大，即系统可以准确地检测出故障。

当系统t＝40s发生乘性故障F2时，其仿真图如图4所示。在出现故障信号时，残差信号会产生很大的变化，其值明显大于所设定的阈值，表明乘性故障F2相对于加性故障更容易检测。

所以采用这种未知输入观测器结合卡尔曼滤波算法的方法可以较好地达到故障检测的效果。

结论

本文将卡尔曼滤波算法引入未知输入观测器进行反馈矩阵的设计，使残差信号更好地抑制噪声的影响，同时达到解耦干扰的效果。通过对风轴转速传感器加性和乘性故障进行仿真，证明所设计的观测器能够有效地检测出风电机组常见转速传感器的故障。

（作者单位：上海电机学院电气学院）

国家自然科学基金（61374136，61473159）；上海人才发展资金（201511）。