磁共振扩散峰度成像研究进展及新应用

沙 淼 赵 欣#* 陈元园 王伟伟 周 鹏# 倪红艳 明 东#

1(天津大学精密仪器与光电子工程学院，天津 300072)2(天津第一中心医院放射科，天津 300192)

磁共振扩散峰度成像研究进展及新应用

沙 淼1赵 欣1#*陈元园1王伟伟1周 鹏1#倪红艳2明 东1#

1(天津大学精密仪器与光电子工程学院，天津 300072)2(天津第一中心医院放射科，天津 300192)

扩散峰度成像(DKI)是一种新兴的扩散磁共振技术，它在传统扩散张量成像的基础上引入了四阶峰度，并以此量化组织中水分子扩散位移概率分布偏离高斯分布的程度，其附加的峰度信息对大脑组织的微观结构更敏感。从扩散峰度成像模型、数据采集参数、模型拟合以及由DKI发展而来的微观结构模型等方面，介绍DKI模型的研究进展和临床应用。最后简要讨论DKI模型存在的问题，并展望其在神经放射学各个方面所具有的广泛深远影响。

扩散峰度成像；非高斯扩散；大脑微结构

引言

扩散磁共振成像(diffusion magnetic resonance imaging，dMRI)是在常规 MRI 基础上发展起来的新技术，通过重建组织中水分子扩散模式来显示其微结构图像，是研究脑组织微结构与连接的重要手段，也是目前已知研究脑组织微结构与连接最有前途的重要手段。扩散磁共振成像最为典型的应用是扩散张量成像(diffusion tensor imaging，DTI)，它通过测定特定方向的扩散行为对脑组织的白质纤维以及纤维束进行评价[1]，从微观层面评估生物组织结构的完整性。但在包含不同种类细胞及其生物膜的复杂而真实的生物组织环境中，水分子的实际扩散会偏离标准的高斯分布，表现为不同程度的非高斯性，以水分子扩散满足高斯分布为假设前提的DTI很难显示纤维交叉、弯曲等复杂微观环境的结构特征[2-3]。扩散峰度成像(Diffusion kurtosis imaging，DKI)是在DTI模型的基础上引入了概率与统计学中定义的四阶峰度(Kurtosis，K)，并以此来量化组织中水分子扩散位移概率分信息[4]，是一种十分有发展前景的实用性临床技术。下面在从DKI模型出发，结合应用较为广泛的DKI成像参数以及新兴的白质微结构模型，讨论DKI在当下科学研究及临床应用中的进展情况，提供未来这项技术潜在的研究价值。

1 扩散峰度成像理论

1.1 扩散现象与峰度系数

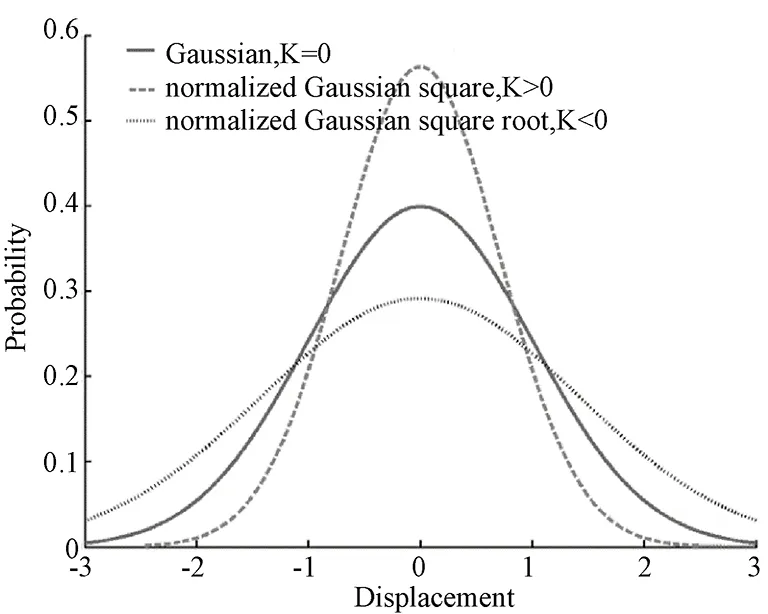
图1 三个各向同性扩散位移概率分布[7]Fig.1 Displacement-probability distribution of three isotropic diffusion[7]

扩散是一种常见的自然现象,它是质量传递的一种基本方式，是由于分子热能激发而使分子发生一种微观、随机的平移运动并相互碰撞。分子的扩散也称为分子的热运动或布朗运动。水分子在给定方向上单位时间内的扩散行为是满足概率分布函数的。在大脑的脑脊液中，水分子扩散行为几乎不受限制，通常被视为自由扩散，扩散概率分布服从高斯分布，但大部分的大脑组织中，水分子通常限制在轴突或树突细胞膜包围的空间结构内，受到周围组织及微观结构(如细胞膜、细胞器、细胞内外的间隔等)的约束[5-6]。当水分子扩散到足够远的距离(当扩散时间在10 ms左右)时，扩散行为受到限制，因此大脑中水分子的扩散概率分布普遍会偏离高斯分布。用来衡量水分子扩散概率分布偏离高斯分布程度的无量纲指标，被称为峰度[4]。如图1所示，深灰色实线表示的是高斯概率分布的曲线，而其他均是偏离高斯的分布。具体来说，K=0代表的即是高斯分布、扩散分布。较高斯分布更陡峭时，对应的峰度值为正(K>0)，而较高斯分布更平缓时，对应的峰度值为负(K<0)，即高峰度值代表了对正常扩散的阻碍程度。在磁共振成像领域中,水分子自由扩散运动(即使在没有浓度梯度的情况下,水分子的扩散运动仍然存在)是磁共振扩散成像的物理基础。峰度值的大小反映了磁共振成像中单个体素内水分子扩散的复杂性，从而反映大脑结构的复杂性与异质性。

1.2 扩散峰度成像数学模型

扩散峰度成像模型是2005年由Jensen等人提出的[4]。针对DTI 假设弱点，他们提出通过扩散信号对扩散系数和峰度系数的双指数拟合，弥补DTI水分子扩散为高斯分布假设的弱点，在考虑其扩散的非高斯分布特性的基础上，建立了一种更为精确的扩散峰度模型，用来拟合水分子的非高斯扩散行为，以便更好地反映组织结构的异质性，更完整地检测脑白质纤维的微结构信息[8-9]。另外，通过对比不同结构组织的峰度值和扩散系数，他们还发现峰度值比扩散系数对组织的结构变化更加敏感[10]。

DKI模型是磁共振信号强度对数关于扩散敏感因子b值的泰勒展开式，仅取二阶前项，其数学描述如下：

ln[S(b)]=ln[S(0)]-bDapp+

(1/6)b2(Dapp)2Kapp+O(b3)

(1)

式中：b表示扩散磁敏感加权因子，b=(γδg)2(Δ-δ/3)，其中γ是旋磁比，g是磁场强度，δ和Δ分别为成像脉冲持续时间和间隔；S为不同b值条件下的信号强度，O为b的高阶无穷小项；Dapp与Kapp分别为某个扩散方向上的表观扩散系数与表观峰度系数。

DKI技术模型是b的二次项，同时它也是对扩散半径敏感的一种模型，因而需采用多b值的采集方式[11]。

1.3 扩散张量与峰度张量

生物组织中的水分子在三维空间中扩散，即不同方向水分子的扩散系数大小相异。用单一标量扩散系数描述空间扩散分布情况显然是不够的。因而,需要一个能够完全描述分子沿各个方向扩散系数的空间矩阵,即扩散张量[12]。扩散张量可准确地描述组织内水分子的扩散状况、各个方向的扩散程度以及扩散的主方向等信息。扩散张量是一个二阶对称矩阵，其空间扩散系数是一个椭球球面，主轴是主特征向量的方向并且与脑神经纤维实际的走向相吻合，而次特征向量的方向表示垂直纤维的走向。由此不难看出，二阶张量的椭球面没有办法解决纤维交叉处(即成像体素内出现两个主要扩散方向时)的纤维走向问题。DKI方法通过在模型拟合中附加一个四阶峰度来弥补二阶张量的这一不足之处。图2形象地描述了峰度张量与扩散张量的关系。

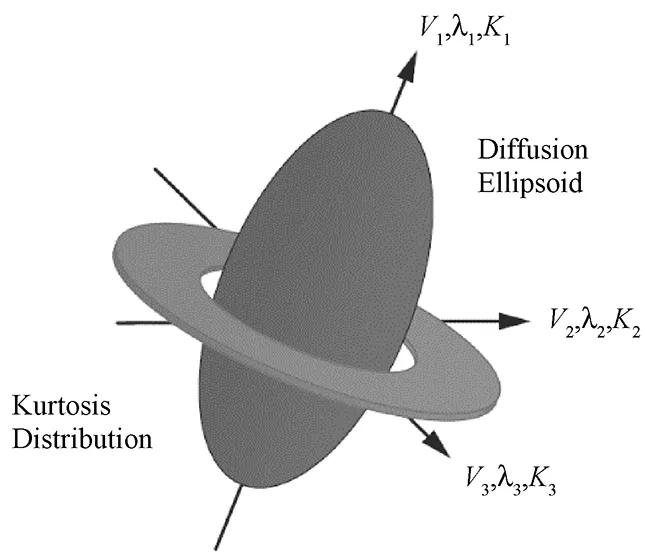
图2 峰度张量与扩散张量的关系[13]Fig.2 The relationship between kurtosis tensor and diffusion tensor[13]

峰度张量既包含水分子主要扩散方向的扩散特性，又可获得垂直于主扩散方向的受限扩散信息。依此峰度张量可更精确检测脑组织微结构，反映复杂结构的组织特性。峰度张量被定义为

(2)

式中，ni,nj,nk,nl表示位移向量n的一个组分，Wijkl为峰度张量中的元素。

通常在生物组织中，扩散峰度的测量依靠扩散敏感梯度方向，在数学表达上通过一个带有15个独立元素的四阶矩阵描述[14-15]。

2 扩散峰度成像的临床实现

2.1 DKI数据采集

不同的生物组织结构，对其内部水分子的扩散运动的影响也不同[3]。扩散加权磁共振成像(diffusion-weighted magnetic resonance imaging，DWI)，就是根据水分子不同的扩散大小影响磁共振信号强度得到其组织结构信息。目前，DKI临床采集序列主要是基于扩散加权磁共振成像序列，临床最为常用的是单次激发SE-EPI(spin echo-echo planar imaging)扩散脉冲序列。在已有的自旋回波序列180°重聚焦脉冲两侧，对称地放置一对大小方向均相等的扩散敏感梯度脉冲，第一个90°脉冲引起质子自旋，当质子沿梯度磁场进行扩散运动时，其自旋频率将发生改变而失去相位。在后一个180°脉冲使质子相位重聚时，由于回波时间内相位分散不能完全重聚，从而导致信号衰减，检测组织中水分子在此方向的扩散程度[16]，可以通过这一序列，利用组织间的扩散系数不同而形成图像。DKI 利用峰度量化非高斯模型下水分子任意分布的概率，不需要完整测量扩散位移分布概率，对梯度硬件、软件均无过高要求。

2.2 DKI临床采集参数

在DWI序列中，设置不同的实验参数可获得不同的水分子扩散信息，其中最重要的参数为扩散敏感梯度方向和扩散敏感因子b值。扩散敏感梯度方向能够提供水分子扩散的方向信息。只有在施加扩散敏感梯度磁场方向上的运动才有MR信号的变化,因此扩散加权图像所反映的水分子扩散运动具有方向性。前面已提到，DKI扩散敏感梯度磁场施加的方向至少为15个，若提高扩散敏感梯度方向的数量，即提高三维空间的采样率，在重建图像时可靠性也可相应上升[17-18]。在DKI实际模型拟合应用上，其模型是b的二次项，在实际采集时为多b值拟合。扩散敏感因子b值是水分子扩散过程对梯度磁场的敏感程度，表征了扩散磁共振信号对扩散的加权程度[19]。扩散速度不同的组织对b值的改变有不同程度的反映，进而在图像上呈现不同的信号特征[20]。b值与施加的扩散敏感梯度的场强、施加的梯度磁场持续时间以及两个梯度磁场间隔的时间相关，有

(3)

式中,γ是旋磁比，g是磁场强度，δ和Δ分别为扩散敏感梯度脉冲持续时间和间隔。

b值越高，对水分子的随机扩散运动越敏感。但b值增高，也伴随着一些矛盾的出现：组织信号衰减更为明显；增高的b值必会延长TE，会产生降低图像信噪比等的不良影响。目前常用的DKI的临床采集，主要采用单次激发多层面自旋回波-回波加权成像序列，进行扩散加权成像，获得横断面、冠状面、矢状面成像数据。采集参数包括 5个b值(500,1 000,1 500,2 000,2 500 s/mm2等间隔采集，除基准b=0)，TR=6 800 ms，TE=101 ms，体素为(2×2×2)mm3，扩散敏感梯度方向为 30个，采集矩阵 128×128，视野(field of view,FOV)为(256×256)mm2。

2.3 DKI模型拟合与张量估计

DKI模型的参数化是通过扩散张量和由旋转不变量提取标量的方式获得的峰度张量来实现的。峰度相关参数值的合理性依赖于对张量估计的准确性，而噪声、头动及图像的失真都会影响张量估计的准确性。理论上，单方向的峰度值有一个比较合理的范围，一般为正值，并且依据不同组织的复杂程度而小于一定的水平，还与使用的b值有关系。但是，对张量估计的误差可能会造成单方向上的峰度值超出可以接受的范围[4]。DKI刚提出时，参数估计采用的是无约束的最小二乘法以及无约束的线性最小二乘法。但是，这些没有约束的方法不能确定能否得到合理的张量估计。Ali Tabesh等人提出使用Cholesky分解对扩散张量进行非负约束的最小二乘法或者线性最小二乘法[10]，这种方法比其他拟合二阶或四阶扩散模型的扩散方程算法更有效。在这种情况下，使用带有线性约束的最小二乘法估计张量这些约束，确保沿扩散敏感梯度方向的扩散系数以及峰度值能在合理可接受的范围内。目前，在DKI模型拟合时常用的软件是Diffusion Kurtosis Estimator(http://www.nitrc.org/projects/dke/)，其中用到的拟合算法就是带约束的线性最小二乘法。

2.4 DKI主要成像参数

DKI理论分析指出,当脉冲持续时间δ趋于无穷小时，式(1)中峰度张量趋近于真实组织内水分子的扩散三维扩散模式，能贴近描述水分子的非高斯扩散行为[21]。与传统的扩散参数相比，DKI 成像参数可以敏感地检测出组织的微结构变化，反映细胞内空间与细胞膜对水分子扩散的相互作用。DKI的主要成像参数包括平均峰度(mean kurtosis，MK)、轴向峰度(axial kurtosis，AK)、径向峰度(radial kurtosis，RK)、峰度分数各向异性(kurtosis anisotropy，KA)以及扩散峰度各向异性(diffusional kurtosis anisotropy，KFA)。

平均峰度MK是反映扩散受限制程度的无量纲的微观结构指标，目前是DKI临床应用中最为常用的指标。MK优势在于它不依赖组织结构的空间方位，脑部灰质、白质结构均可以应用平均峰度进行描述[22]。MK有两种定义方式，一种是沿不同扩散敏感梯度方向上的表观峰度系数的平均值，有

(4)

式中, (Kapp)i是沿第i个方向上的表观扩散峰度，n是采集DWI数据时扩散敏感梯度方向的个数。

另一种定义MK是基于扩散张量3个本征向量方向的峰度值，有

(5)

式中，K1、K2、K3为沿扩散椭球3个特征方向的峰度值。

MK大小取决于感兴趣区域内组织结构的复杂程度，即成像体素内生物组织结构越复杂，水分子扩散偏离高斯分布程度越大，平均峰度的数值也越大。

轴向峰度AK是指沿着扩散椭球轴向的峰度值(最大特征值的方向)，即

AK=K1

(6)

在脑白质中，由于水分子沿着突触方向扩散是自由不受限制的，偏离高斯分布的程度最小，因此AK值比较小。

径向峰度RK是指在主要扩散正交方向上的峰度的平均值，即

(7)

RK是一个十分重要的参数指标，因为扩散受限主要是在径向，故峰度为非零数值，且在径向表现得尤为突出。特别是在脑白质中，由于细胞膜和髓鞘的阻挡，水分子扩散受到限制，显著地偏离高斯分布，相对于DTI得到的部分分数各向异性参数的变化，RK增大得更为显著。AK和RK这两个有方向的峰度与MK并不是简单的线性关系，这是因为四阶峰度张量的三维分布不能用简单的椭球来表示[23]。

峰度各向异性KA在某种程度上类似于DTI中的分数各向异性FA指标，可由峰度的标准偏差给出，有

(8)

其中

(9)

式中，Ki表示沿 DTI 椭球体的3个主轴方向的峰度值。

KA 越小，表示越趋于各向同性扩散; 若组织结构越紧密越规则，KA 越大。影响 KA 的因素有介质的黏度、分子间距离、邻近血管搏动或脑脊液流动、纤维结构的完整性、平行性及致密程度等。

扩散峰度各向异性KFA是用于提供补充分数各向异性FA信息的参数，反映了各扩散组分在空间分布中的差异性，且不依赖于扩散敏感梯度方向的成像参数[24]。KFA在纤维交叉处优势更明显，其表达式为

(10)

3 基于DKI的白质微结构模型

DKI模型在扩散椭球模型基础上叠加峰度信息，使之可更精确地检测脑组织微结构，更好地反映大脑微结构的信息。利用这一优势，研究者通过建立一系列基于DKI的白质微结构模型，有效地克服了单纯依靠显微镜观察解剖和手术标本的传统组织微结构检测手段创伤性大、难于在活体实施的弊端。这些模型主要包括白质纤维束完整性模型、扩散峰度-取向分布函数模型、神经组织的峰度分析模型。

3.1 白质纤维束完整性模型

2011年，ElsFieremans等人提出基于DKI的脑白质扩散模型(见图3，θA和θB分别代表纤维方向与扩散方向的夹角)，用于分析神经轴突内、外两个互不对流的隔离区域内水分子扩散现象[25]。

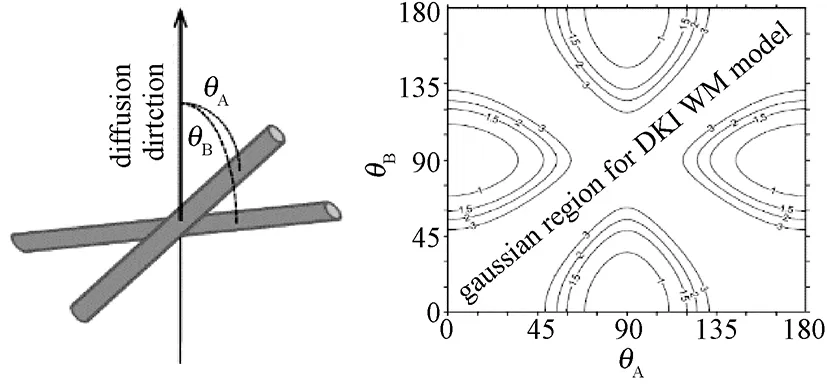
图3 交叉纤维白质完整性模型[25]。(a)两纤维交叉的高斯模型；(b)不同轴突水分数下θA和θB的关系Fig.3 White matter integrity model of crossing fiber[25]. (a) Gaussian model of two-fiber crossing；(b) The relationship between θAand θBunder Different axonal water fraction

这一白质模型基于两个假设前提：其一，白质区域皆由两个互不对流的房室(轴突内区域和轴突外区域)组成；其二，每个房室内水分子的扩散过程均近似于高斯分布。如此假设后，虽然整个白质区域仍存在扩散限制，但在各个隔区内皆可方便地使用已有较成熟的扩散张量来描述每个隔区的扩散行为。下面是该白质扩散模型的基本数学描述，有

(11)

式中，f是由峰度信息得到的轴突内区域扩散所占的权重。

基于该模型，DKI可借助隔区内扩散张量3个本征方向的扩散信息，结合隔区外峰度信息，获得体素的轴突内外区的投影分布；同时可由两个隔区的扩散张量得到各自扩散轴向与径向的扩散系数，并作为成像参数进行脑白质成像。研究结果表明，这种方法能够更好地评估轴突内外区的扩散特性和轴突外区的几何形变程度。但是，该大脑白质扩散模型过于理想化：很多白质扩散情况未明确涵盖，其中脑脊液就不能视为单独隔区；使用小b值、少扩散方向数据，会受到信息量不足的影响[26-27]。如图4所示，由白质纤维束完整性模型得到大脑参数图。

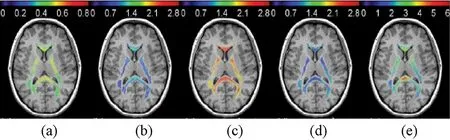
图4 典型脑白质区域参数图[25]。(a)轴突内水分子分数；(b)轴突内扩散系数；(c)轴向轴突内扩散系数；(d)径向轴突内扩散系数；(e)轴突内曲率。Fig.4 Mapping of typicalbrain white matter regions[25].(a) The axonal water fraction; (b) The axonal diffusivity; (c) The axial extra-axonal space diffusivity; (d) the radial extra-axonal space diffusivity; (e) The tortuosity of extra-axonal space

3.2 扩散峰度-取向分布函数模型

DKI 相比以往传统的扩散成像技术，最突出的优势是对组织细微结构的改变更敏感，因此在神经纤维跟踪成像上的优势亦明显[28]。Mariana Lazar和他的同事将取向分布函数(orientation distribution function，ODF)与扩散峰度之间建立了数学关系，提出了一个基于扩散的扩散峰度近似信号计算取向分布函数的方法，有

(12)

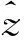
任何一个给定方向的取向分布函数，可以近似通过对一个依赖垂直于轴向方向上的扩散系数和峰度系数的函数进行积分来求得。正如上面的公式，既包含高斯扩散的贡献，又融合了非高斯扩散的信息，因此这个扩散峰度-取向分布函数能够解决纤维交叉的问题，如图5所示。

图5 取向分布函数的三维表面扩散模型估计两交叉(上)和三交叉(下)纤维[28]。(a)实际的ODF；(b)DK估计的ODF；(c)实际非高斯的ODF；(d)DK估计的非高斯ODF；(e)Q-ball估计的PDF；(f)高斯估计的ODF；绿色的细线为纤维的方向Fig.5 Diagram of three-dimensional surfaces of the exact and estimated ODFs for diffusion models with two (upper) and three (bottom) equally contributing intersecting fibers[28].(a)Exact ODF；(b)DK estimation of the ODF；(c)Exact NG-ODF；(d)DK estimation of the NG-ODF；(e)Q-ballestimation of the ODF；(f)Gaussian estimation of the ODF. The directions of the component fibers are shown by green lines

图6 基于DKI神经纤维的跟踪图。(a)基于DKI的全脑取向分布函数，白色方框表示选取的局部感兴趣区域；(b)基于DKI的局部取向分布函数，箭头表示重建方向；(c)神经纤维跟踪,白色方框表示选取的局部感兴趣区域Fig.6 Diagram of DKI fiber tracking.(a) DKI-based ODF of whole brain,white box represents selected local region of interest；(b)DKI-based ODF of localregion, arrow represents reconstruction direction；(c) Fiber tracking,white box represents selected local region of interest

值得注意的是，扩散峰度-取向分布函数这一模型也存在局限性。例如，扩散峰度-取向分布函数的方法不能用于重建取向分布函数带有高频分量的纤维架构。虽然，这种高频成分对于少量的纤维交叉区域不会产生很巨大的影响，但高频成分将会被误认为纤维交叉数量的增加，在纤维跟踪时会出现极大偏差，特别是影响纤维跟踪的准确性。

随着DKI模型拟合以及ODF计算稳定性的提高，DKI在神经纤维成像方面的研究越来越受到重视，图6为DKI在纤维交叉处的跟踪效果。

相比传统的扩散张量成像，DKI在纤维交叉处有独特的分辨能力。2014年，一些学者对比了峰度张量与基于峰度的取向分布函数在神经纤维跟踪成像上的效果，峰度张量在表征胼胝体(特别是接近皮层的脑区)时，灵敏度、准确性明显高于基于峰度的取向分布函数[29]。这一研究也从侧面证实，四阶峰度张量在检测成像体素内多非高斯扩散现象时的优势。2015年，一些关于DKI纤维跟踪方法的研究涌现出来，包括对峰度-取向分布函数估计优化算法的研究，提取可用于纤维跟踪效果评价的量化参数，等等[30-32]。

3.3 神经组织的峰度分析模型

神经组织的峰度分析模型(kurtosis analysis of neural diffusion organization，KANDO)是2015年由Edward S. Hui等提出的方法，是将峰度张量和扩散张量作为输入参量来构建组织的微结构模型[33]。KANDO的基本假设前提是生物组织由N+1个不可交换的隔室组成，且每一个房室内的水分子扩散都服从高斯分布，均可由扩散张量描述。然而，其他类型细胞的存在(如星型胶质细胞)，会大大缩短模型之间的交换时间。当交换时间小于扩散时间时，细胞室可以看作是在快速交换与细胞外空间,然后有效地整合成包括细胞外空间和可能的其他细胞间快速交换的房室。由于胶质细胞与无髓鞘的神经突的交换时间是有限的，所以模型与细胞之间交换的准确性是模糊不清的。当隔室之间的交换时间与扩散时间相当时，隔室之间的交换便起到主要的作用。KANDD是从代表单一白质、交叉白质和灰质3个简单的模型出发，模型的数学表达为

(13)

式中，N+1是隔室的数量。

从模型本身可以看出，KANDO适应于存在多高斯组分交叉的组织结构，采用描述神经组织的非高斯扩散模式，且适合作为DKI的补充以完善其指标的可解释性，见图7。同时，KANDO方法所得的指标是通过神经微结构特征来描述神经病理损伤的有效生物标记，图8是各房室神经组织成像的示意图。

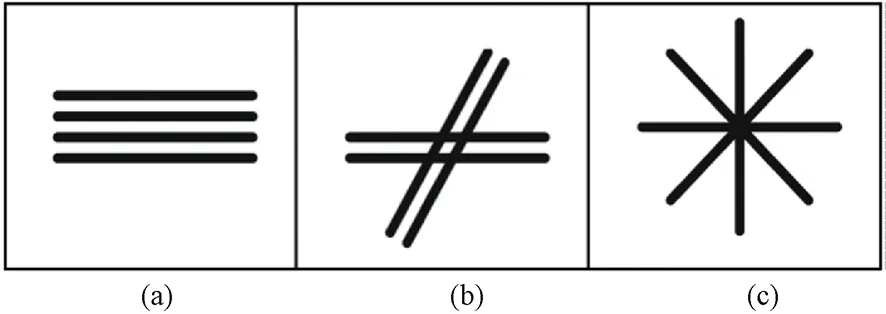
图7 KANDO三种简单的纤维取向的示意图[33]。(a)在一个给定的体素内轴突纤维是单向的；(b)有两个不同的方向的交叉纤维束；(c)各向同性分布的轴突和树突取向Fig.7 Schematic illustrating the fiber orientations utilized for three examples of KANDO[33].(a)The axonal fibers within a given voxel are taken to be unidirectional；(b)Intersecting fiber bundles with up to two distinct directions;(c)An isotropic distribution of axon and dendrite orientations

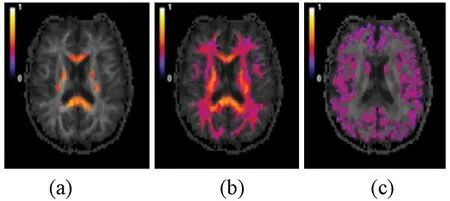
图8 三房室假设下神经组织成像示意图[33]。(a)单一方向纤维的神经内扩散率；(b)两方向轴突纤维的神经内扩散率；(c)各向同性分布的轴突和树突取向的神经内扩散率Fig.8 Diagram of three compartments under assumptions nerve tissue imaging[33]. (a) Intrinsic intra-neurite diffusivity of unidirectional axonal fibers;(b) Intrinsic intra-neurite diffusivity of two distinct directional axonal fibers;(c) Intrinsic intra-neurite diffusivity of an isotropic distribution of axon and dendrite orientations

4 DKI临床应用

在异质性扩散与组织微观结构方面，DKI技术检测是一项十分敏感且具有特异性的技术。它通过提供水分子的相关物理特征(如黏度、弹性、渗透率、密度及扩散率等的峰度信息)，反映生物组织成分和结构形态，为实现组织微结构检测提供科学依据[34-35]。DKI技术最初是专门应用于大脑成像[25,36-37]，近年来因其组织微结构表征敏感性强的优势，也开始应用于除大脑外的其他部位疾病的检测与诊断。

4.1 脑部扩散峰度成像

作为对传统DTI的扩展，DKI过去在一定程度上是一种对大脑组织复杂性的测量手段；之前的研究已经证明，组织微观结构复杂性的提高是源于神经胶质的活动以及反应性星形细胞的胶质化，神经元的丧失会导致峰度值的减小。因此，近年来DKI在研究大脑发育与老化、中风、脑肿瘤以及神经退行性疾病方面极富潜力。

经DKI模型探测可以发现，从青春期到成年期，大脑额叶皮层的MK随之增加，这对应于在这一发育过程中大脑持续的髓鞘化以及微观结构的复杂性逐渐提高。随着年龄的进一步增长，平均峰度MK反而逐渐降低，这一点与神经退行性变化与收缩有关，原因是前额叶皮层的变化与认知的水平、大脑运动模式变化相关。DKI技术用于大脑发育的另一大优势在于可选用的感兴趣区域，包含更大范围的额叶，利用峰度指标可以细化并同时评价区域内的灰质、白质[5]。

DKI技术检测在异质性扩散与组织微观结构方面是一项十分敏感且具有特异性的技术，在中风缺血部位的识别有明显的特异性[8,38-41]。2015年，Weber等分别采用经典扩散张量成像得到的扩散系数和扩散峰度参数，分析了中风引起的微结构改变，同时指出两种测量指标很可能对病理结构的变化具有不同的时间特异性，需要做进一步的生理物理基础研究[42]。

在脑肿瘤的检测研究中，DKI指标参数可能已成为检测出差异的唯一扩散指标。Van Cauter等人[43-44]通过对比采集28个原发性脑瘤的病人由扩散加权成像得到的成像数据，经DKI模型计算求得的参数，包括MD、MK、FA、RK、AK图像，发现发育成熟阶段的肿瘤细胞的峰度参数相比发育初期的肿瘤细胞高一些。这可能是随着肿瘤细胞的不断发育成长，由于细胞的密度增加、细胞的尺寸减小、细胞内的微环境趋向于复杂化等原因造成的，DKI数据能够提供探测不同肿瘤细胞微观结构差异的更多的图像信息。

将DKI应用于阿尔兹海默症中，能够提供较传统DTI更多的信息，对阿尔兹海默症的深入研究是很有意义的[45-46]。相关研究显示，使用DKI以及分别统计灰质和白质的方法，可以观察到阿尔兹海默症以及轻度认知障碍病人的大脑顶叶以及枕叶之间扩散系数和峰度系数均有显著的差异[47]。DKI指标参数与细微精神状态检查有明显的相关性。这些现象都提示，DKI的方法能够提供敏感的影像学生物标志，用于评估认知障碍的严重性，并且能够有效地提高阿尔兹海默症的早期发现与诊断的进程。ElsFieremans和Andreana Benitez等人分别研究了DKI对白质结构的微观建模及其在病理研究中的显著价值，充分说明DKI对于白质完整性的精确检测[25,48]。

4.2 体部扩散峰度成像

近年来的研究显示，DKI技术已应用于人体其他部位疾病的研究与诊断中[49-50]，这一发展有助于更好地理解多b值拟合的DKI(特别是峰度)在生物组织扩散过程中的潜在生理意义。在临床应用中，焦点在于评价最大b值对体扩散峰度成像质量与表征病变能力的影响。

关于DKI在前列腺癌的诊断和治疗中的研究大量涌现[51-54]。引入峰度指标，可提高传统DTI参数识别良性和恶性前列腺肿瘤的准确性，也有助于改进对肿瘤恶性程度的分辨能力[49-55]。2014年，ShitengSuo等运用DKI，很好地反映了前列腺疾病的非高斯扩散特征，结果证实扩散峰度成像模型能够较为准确地描述扩散信号的衰减，其峰度参数也能较为精准地鉴别靶区周围组织的良、恶性[56]。该研究的结果同时也显示，靶区周围组织扩散特征与峰度特征亦有可能呈负相关。但值得注意的是，这些研究均表明，DKI中的最大b值将会不同程度地影响对肿瘤的识别能力，主要原因是水分子在生物组织中的扩散相互作用在较高b值时表现得较为明显。2项关于DKI在乳腺疾病上的检测研究选择最大b值为2 000～3 000 s/mm2，并发现纤维肿瘤和乳腺纤维囊性改变仅表现在峰度值的差异上[57-58]。2006年，Trampel等人已将DKI技术应用于超极化He对肺部小气道病变检测的研究中，并发现仅峰度值发生变化[59]。此外，相关研究表明，DKI中最大b值过小会严重影响峰度值在表征病变部位的准确性和可行性[60-61]。相比单指数模型(如DTI)，DKI在肝脏部位的研究表明，其对扩散加权信号衰减有更好的拟合效果[50]。

5 总结与展望

从高斯扩散发展到非高斯扩散，DKI更加复杂和接近组织微环境中的水分子真实扩散模型，并向着探测更加精细组织微结构信息(不仅在脑白质研究中而且在灰质中极富潜力)的方向快速发展着。然而，DKI技术尚有其局限性，有待于今后研究改进并更深入地发展。第一，目前的扩散磁共振技术所能达到的空间分辨率(即磁共振信号采集时体素的尺寸)一般为1～3 mm，而神经纤维的尺寸为0.1～100 μm，通常存在弯曲、分支、交叉等复杂结构。即便DKI技术能够反映真实的水分子扩散现象，也仅仅是定性分析，并不能做到精准测量。在现有扩散磁共振技术发展的基础上，建立完善能够获取更精确、更高空间分辨率的纤维结构信息以及提供特异性更高的参数，为促进DKI的丰富和发展具有巨大的实际应用价值。第二，DKI模型自2005年提出，其模型的稳定性与可靠性一直存在质疑，虽然已有大量提高模型稳定性的研究出现，但仍需在模型拟合的算法和采集方案上进行一定的优化。第三，基于多磁共振扩散敏感因子b值的非高斯扩散成像在复杂组织结构检测与重建方面，突破了传统高斯模型的局限，提供了组织微结构检测的多种新指标，是扩散磁共振成像技术发展与临床研究的热点方向。然而，非高斯扩散潜在的生物物理过程尚不完全清楚，有关峰度的生理意义、峰度与扩散信息的内在联系等基本概念至今都未能给出明确答案。目前，只能较笼统地将峰度概念的引入理解为描述复杂白质微结构的补充措施。DKI在挖掘脑组织的微观各向异性结构信息方面，显示出其独特的优势，但需扩展和深化针对神经元、神经胶质细胞、树突等组织微结构细节的理解与描述，以便为临床提供能与微观结构特征相结合的生理、病理解释依据，使其能更广泛地应用于各种神经组织系统的疾病。

[1] Hui ES, Cheung MM, Chan KC, et al. B-value dependence of DTI quantitation and sensitivity in detecting neural tissue changes[J]. Neuroimage, 2010, 49(3): 2366-2374.

[2] Tuch DS, Reese TG, Wiegell MR, et al. Diffusion MRI of complex neural architecture[J]. Neuron, 2003, 40(5): 885-895.

[3] Basser PJ, PierpaoliC.Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI[J]. Journal of Magnetic Resonance, 2011, 213(2): 560-570.

[4] Jensen JH, Helpern JA, Ramani A, et al., Diffusional kurtosis imaging: The quantification of non-gaussian water diffusion by means of magnetic resonance imaging[J]. Magnetic Resonance in Medicine, 2005, 53(6): 1432-1440.

[5] Gong NJ, Wong CS, Chan CC, et al. Aging in deep gray matter and white matter revealed by diffusional kurtosis imaging[J]. Neurobiology of Aging, 2014, 35(10): 2203-2216.

[6] Veraart J, van Hecke W, Sijbers J, et al.Constrained maximum likelihood estimation of the diffusion kurtosis tensor using a rician noise model [J]. Magn Reson Med, 2011, 66(3): 678-686.

[7] Basser PJ, Mattiello J, LeBihan D,et al. Estimation of the effective self-diffusion tensor from the NMR spin echo[J]. Journal of Magnetic Resonance, Series B, 1994. 103(3): 247-254.

[8] Rudrapatna SU, Wieloch T, Beirup K, et al. Can diffusion kurtosis imaging improve the sensitivity and specificity of detecting microstructural alterations in brain tissue chronically after experimental stroke? Comparisons with diffusion tensor imaging and histology[J]. Neuroimage, 2014, 97: 363-373.

[9] Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis[J]. NMR in Biomedicine, 2010, 23(7): 698-710.

[10] Poot DH, Den Dekker AJ, Achten E, et al., Optimal experimental design for diffusion kurtosis imaging[J]. IEEE Trans Med Imaging, 2010, 29(3): 819-829.

[11] Assemlal HE, Tschumperle D, Brun L, et al. Recent advances in diffusion MRI modeling: angular and radial reconstruction [J]. Med Image Anal, 2011, 15(4): 369-396.

[12] Basser PJ, Mattiello J. MR diffusion tensor spec- troscopy and imaging[J].Biophysica,1994,66:259-267.

[13] Steven AJ, Zhuo J, Melhem ER. Diffusion kurtosis imaging: an emerging technique for evaluating the microstructural environment of the brain[J]. American Journal of Roentgenology, 2014. 202(1): 26-33.

[14] Qi L, Wang Y,Wu E. D-eigenvalues of diffusion kurtosis tensors[J]. Journal of Computational and Applied Mathematics, 2008. 221(1): 150-157.

[15] Fukunaga I, Hori M, Masutani Y, et al. Effects of diffusional kurtosis imaging parameters on diffusion quantification [J]. Radiol Phys Technol, 2013, 6(2): 343-348.

[16] 俎栋林, 核磁共振成像学[M]. 北京: 高等教育出版社，2004.

[17] Yan X, Zhou M, Ying L, et al., Evaluation of optimized b-value sampling schemas for diffusion kurtosis imaging with an application to stroke patient data[J]. Computerized Medical Imaging and Graphics, 2013, 37(4): 272-280.

[18] Grebenkov DS. Exploring diffusion across permeable barriers at high gradients. II. Localization regime[J]. Journal of Magnetic Resonance, 2014, 248: 164-176.

[19] Güllmar D, Haueisen J, Reichenbach JR. Analysis of b-value calculations in diffusion weighted and diffusion tensor imaging[J]. Concepts in Magnetic Resonance Part A, 2005. 25(1): 53-66.

[20] Mulkern RV, Haker SJ, Maier SE. On high b diffusion imaging in the human brain: ruminations and experimental insights[J]. Magnetic Resonance Imaging, 2009, 27(8): 1151-1162.

[21] Minati L, Aquino D, Rampoldi S, et al. Biexponential and diffusional kurtosis imaging, and generalised diffusion-tensor imaging (GDTI) with rank-4 tensors: A study in a group of healthy subjects[J]. Magnetic Resonance Materials in Physics, Biology and Medicine, 2007, 20(5-6): 241-253.

[22] Cheung MM, Hui ES, Chan KC, et al. Does diffusion kurtosis imaging lead to better neural tissue characterization? A rodent brain maturation study[J]. Neuroimage, 2009, 45(2): 386-392.

[23] Das SK, Wang JL, Bing L,et al. Regional values of diffusional kurtosis estimates in the healthy brain[J]. Journal of Magnetic Resonance Imaging, 2013, 37(3): 610-618.

[24] Glenn GR, Helpern JA, Tabesh A, et al. Quantitative assessment of diffusional kurtosis anisotropy[J]. NMR in Biomedicine, 2015, 28(4): 448-459.

[25] Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging [J]. Neuroimage, 2011. 58(1):177-188.

[26] Blockx I., De Groof G, Verhoye M, et al. Microstructural changes observed with DKI in a transgenic Huntington rat model: evidence for abnormal neurodevelopment [J]. Neuroimage, 2012. 59(2): 957-967.

[27] Arcienega II., Brunet JF, Bloch J, et al. Cell locations for AQP1, AQP4 and 9 in the non-human primate brain[J]. Neuroscience, 2010. 167(4): 1103-1114.

[28] Lazar M, Jensen JH, Xuan L, et al. Estimation of the orientation distribution function from diffusional kurtosis imaging[J]. Magnetic Resonance in Medicine, 2008, 60(4): 774-781.

[29] Henriques RN, Correia MM, Nunes RG, et al.Exploring the 3D geometry of the diffusion kurtosis tensor: Impact on the development of robust tractography procedures and novel biomarkers[J]. NeuroImage, 2015, 111: 85-99.

[30] Glenn GR, Helpern JA, Tabesh A, et al. Optimization of white matter fiber tractography with diffusional kurtosis imaging[J]. NMR in Biomedicine, 2015, 28(10): 1245-1256.

[31] Jensen JH, Helpern JA. Resolving power for the diffusion orientation distribution function[J]. Magnetic Resonance in Medicine, 2015.

[32] Jensen JH, Helpern JA, Tabesh A. Leading non-Gaussian corrections for diffusion orientation distribution function[J]. NMR in Biomedicine, 2014, 27(2): 202-211.

[33] Hui ES, Russell Glenn G, Helpern JA, et al. Kurtosis analysis of neural diffusion organization[J]. Neuroimage, 2015. 106: 391-403.

[34] Pierpaoli C,Basser PJ. Toward a quantitative assessment of diffusion anisotropy [J]. Magnetic Resonance in Medicine, 1996. 36(6): 893-906.

[35] Kelm ND, West KL, Carson RP, et al. Evaluation of diffusion kurtosis imaging in ex vivo hypomyelinated mouse brains[J]. NeuroImage, 2016, 124: 612-626.

[36] Raab P, Hattingen E, Franz K, et al.Cerebral gliomas: Diffusional kurtosis imaging analysis of microstructural differences[J]. Radiology, 2010, 254:876-881.

[37] Wu EX, Cheung MM. MR diffusion kurtosis imaging for neural tissue characterization[J]. NMR Biomed, 2010, 23:836-848.

[38] Sun P Z, Wang Y, Mandeville E, et al. Validation of fast diffusion kurtosis MRI for imaging acute ischemia in a rodent model of stroke[J]. NMR Biomed, 2014, 27(11): 1413-1418.

[39] Wu Y, Kim J, Chan ST, et al. Comparison of image sensitivity between conventional tensor-based and fast diffusion kurtosis imaging protocols in a rodent model of acute ischemic stroke[J]. NMR Biomed, 2016,29(5): 625-630.

[40] Grinberg F, Farrher E, Ciobanu L, et al. Non-Gaussian diffusion imaging for enhanced contrast of brain tissue affected by ischemic stroke[J]. PLoS ONE, 2014, 9(2): e89225.

[41] Hui ES, Fieremans E, Jensen JH, et al. Stroke assessment with diffusional kurtosis imaging[J]. Stroke, 2012, 43(11): 2968-2973.

[42] Weber RA, Hui ES, Jensen JH, et al. Diffusional kurtosis and diffusion tensor imaging reveal different time-sensitive stroke-induced microstructural changes[J]. Stroke, 2015, 46(2): 545-550.

[43] van Cauter S, Veraart J, Sijbers J, et al.Gliomas: Diffusion kurtosis MR imaging in grading[J]. Radiology, 2012, 263(2): 492-501.

[44] van Cauter S, De Keyzer F, Sima DM, et al. Integrating diffusion kurtosis imaging, dynamic susceptibility-weighted contrast-enhanced MRI, and short echo time chemical shift imaging for grading gliomas[J]. Neuro-Oncology, 2014, 16(7): 1010-1021.

[45] Struyfs H, Van Hecke W, Veraart J, et al. Diffusion kurtosis imaging: A Possible MRI biomarker for AD diagnosis?[J]. Journal of Alzheimer′s Disease, 2015, 48(4):937-948.

[46] Lee SH, Coutu JP, Wilkens P, et al. Tract-based analysis of white matter degeneration in alzheimer′s disease[J]. Neuroscience, 2015, 20(301):79-89.

[47] Gong NJ, Wong CS, Chan CC,et al.Correlations between microstructural alterations and severity of cognitive deficiency in Alzheimer's disease and mild cognitive impairment: a diffusional kurtosis imaging study[J]. Magnetic Resonance Imaging, 2013. 31(5): 688-694.

[48] Benitez A, Fieremans E, Jensen JH, et al. White matter tract integrity metrics reflect the vulnerability of late-myelinating tracts in alzheimer′s disease [J]. Neuroimage: Clinical, 2014, 4:64-71.

[49] Rosenkrantz AB, Sigmund EE, Johnson G, et al. Prostate cancer: Feasibility and preliminary experience of a diffusional kurtosis model for detection and assessment of aggressiveness of peripheral zone cancer[J]. Radiology, 2012(264):126-135.

[50] Anderson SW, Barry B, Soto J,et al. Characterizingnon-Gaussian high b-value diffusion in liver fibrosis: stretched exponential and diffusional kurtosis modeling[J]. Journal of Magnetic Resonance Imaging, 2014(39):827-834.

[51] Katahira K, Takahara T, Kwee TC, et al. Ultra-high-b-value diffusionweighted MR imaging for the detection of prostate cancer: Evaluation in 201 cases with histopathological correlation[J]. European Radiology, 2011,21:188-196.

[52] Kitajima K, Kaji Y, Kuroda K,et al.High b-value diffusionweighted imaging in normal and malignant peripheral zone tissue of the prostate: effect of signal-to-noise ratio[J]. Magnetic Resonance Medicine,2008,7:93-99.

[53] Kim CK, Park BK, Kim B. High-b-value diffusion-weighted imaging at 3T to detect prostate cancer: comparisons between b values of 1,000 and 2,000 s/mm2[J]. American Journal of Roentgenology, 2010,194:33-37.

[54] Rosenkrantz AB, Kong X, Niver BE, et al. Prostate cancer: comparison of tumor visibility on trace diffusion-weighted images and the apparent diffusion coefficient map [J].American Journal of Roentgenology, 2011,196:123-129.

[55] Tamura C, Shinmoto H, Soga S, et al. Diffusion kurtosis imaging study of prostate cancer: preliminary findings[J].Journal of Magnetic Resonance Imaging, 2014,40:723-729.

[56] Suo S, Chen X, Wu L, et al. Non-Gaussian water diffusion kurtosis imaging of prostate cancer[J]. Magnetic Resonance Imaging, 2014, 32:421-427.

[57] Nogueira L, Brandao S, Matos E, et al. Application of the diffusion kurtosis model for the study of breast lesions[J].European Radiology, 2014,24: 1197-1203.

[58] Wu D, Li G, Zhang J,etal.Characterization of Breast Tumors Using Diffusion Kurtosis Imaging (DKI)[J]. PLoS ONE, 2014(9):e113240.

[59] Trampel R, Jensen JH, Lee RF, et al. Diffusional kurtosis imaging in the lung usinghyperpolarized 3He[J].Magnetic Resonance Medicine,2006,56:733-737.

[60] Pentang G, Lanzman RS, Heusch P, et al. Diffusion kurtosis imaging of the human kidney: A feasibility study[J]. Magnetic Resonance Imaging, 2014,32:413-420.

[61] Huang Y, Chen X, Zhang Z, et al. MRI quantification of non-Gaussian water diffusion in normal human kidney: A diffusional kurtosis imaging study[J]. NMR Biomed, 2015,28:154-161.

Research and Novel Application on MR Diffusion Kurtosis Imaging

Sha Miao1Zhao Xin1#*Chen Yuanyuan1Wang Weiwei1Zhou Peng1#Ni Hongyan2Ming Dong1#

1(SchoolofPrecisionInstrumentandOpto-ElectronicsEngineering,TianjinUniversity,Tianjin300072,China)2(DepartmentofRadiology,TianjinFirstCenterHospital,Tianjin300192,China)

As an emerging technology of diffusion MRI, diffusion kurtosis imaging (DKI) introduces forth-order tensor to quantify the degree to non-Gaussian water diffusion in biologic tissues. Additional kurtosis information on the water diffusion properties could be more sensitive to tissue microstructure in the brain. This paper introduced diffusion kurtosis model, data acquisition parameters, model fitting and microstructural model based on DKI to reveal research development and clinical application of DKI model. Meanwhile, limitations of DKI model and prospect of its profound influence on all aspects of neural radiology were discussed as well.

diffusion kurtosis imaging (DKI); non-Gaussian diffusion; cerebral microstructure

10.3969/j.issn.0258-8021. 2016. 03.010

2016-01-19， 录用日期:2016-04-06

国家自然科学基金(81571762)；天津市自然科学基金青年项目(13JCQNJC14400)

R318

A

0258-8021(2016) 04-0460-010

# 中国生物医学工程学会会员(Member, Chinese Society of Biomedical Engineering)

*通信作者(Corresponding author)， E-mail: zhaoxin@tju.edu.cn