二阶广义积分单相电网电压锁相方法实验研究

谢门喜, 史炳伟

(苏州大学 智能结构与系统研究所，江苏 苏州 215006)

二阶广义积分单相电网电压锁相方法实验研究

谢门喜, 史炳伟

(苏州大学 智能结构与系统研究所，江苏 苏州 215006)

并网型电力电子变流设备需要精确检测电网电压的相位实现同步。同步旋转坐标方法是一种针对三相电网电压优良锁相方案，基于二阶广义积分方法构造一虚拟正交信号，能将同步旋转坐标方法扩展至单相电网锁相。分析了控制流程，参数选择，以DSP F28335为控制核心的实验平台实现算法，得出电网电压幅值突变、频率突变、谐波情况下的响应结果，验证了方法的正确性。

锁相环；同步旋转坐标变换；正交信号发生器；二阶广义积分；数字信号处理器；实验研究

0 引 言

随着灵活交流输电系统FACTS技术发展，大量电力电子设备并入公用电网，对电网电压相位实时检测是一项基本的技术，如何高精度、快速的锁相是整个控制系统极其重要的一环。经典锁相环结构包含三部分：鉴相器检测出输出信号输入信号之间的相位偏差，环路滤波器消除相位偏差中的高频成分，振荡器利用偏差稳态量计算相位信息，通过不断的闭环调整，使得输出信号跟踪输入信号，直到两者之间的偏差为一恒定值。基于这一基本结构框架，同步旋转坐标系下的锁相方法(SRF-PLL)已成为一种主流的实用化方法，该方法最初应用于三相电网电压锁相[1-2]，将三相电网电压信号从静止abc坐标变换到二相旋转dq坐标，利用d轴电压分量为零这一特性实现鉴相，得到电网电压实际相角与观测相角的偏差，带有低通特性的滤波器对偏差运算出修正量，加上基频后，观测到频率信号，进而得到实时角度信息。

本文首先介绍了SRF-PLL方法的基本原理，利用二阶广义积分构造正交信号以实现SRF-PLL方法对单相电网电压的锁相。最后，实验测试平台，给出了电网电压幅值突变、频率突变、谐波情况下的响应结果。

1 同步旋转锁相技术

若单相电网电压信号为：

v=Vmsinωt=Vmsinθ

(1)

其中θ为电网电压的实时相位角，单位rad，是待检测量；Vm为电网电压的幅值，单位V。

如果能够精确构造出一个信号qv′，幅值大小与v相等，相位滞后v90°，形成：

(2)

引入变换矩阵：

(3)

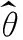
将变换矩阵式(3)左乘式(2)，化简：

(4)

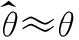
(5)

(5)式表明，vd与相位偏差是线性关系，利用vd作为鉴相器，作为环路滤波器的输入，振荡器产生观测角度信号，如图1所示。

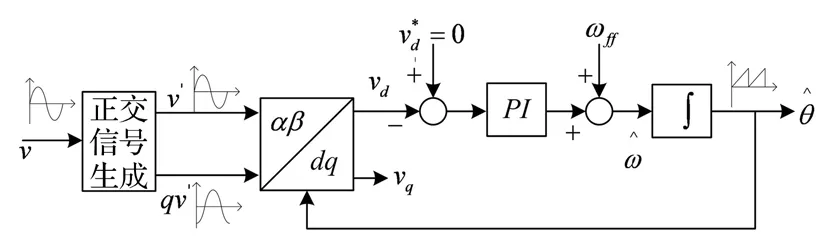
图1 同步旋转坐标系下的锁相方法

在图1中，单相电网输入信号仅有一个正弦波，所含的信息量较少，利用SRF-PLL方法对单相电网电压锁相时，需要构造一与输入信号v幅值相等，相位相差90°的正交信号qv′，形成αβ分量。常用的正交信号生成方法是将输入信号滞后四分之一周期，但这会使得整个PLL响应相应变慢四分之一周期，在快速性要求比较高的场合，这一固有延时是无法接受的。文献[3]提出了基于二阶广义积分(Second Order Generalized Integrate)获得正交信号的方法，其基本结构如图2所示，对输入信号v与输出信号v′相减，乘以系数k，利用二阶广义积分实时构造出qv′，实现了输入

信号与输出信号的正交化，同时对输入信号兼有滤波效果[4]。

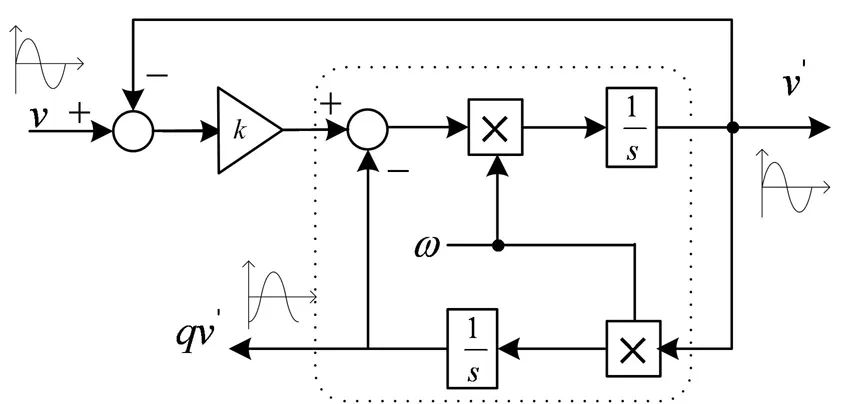
图2 基于二阶广义积分的正交信号生成器

2 二阶广义积分正交信号发生器

两路正交信号对输入信号v的传递函数为：

(6)

(7)

其中ω=2π50 Hz=314 rad/s，k是待定系数，其取值大小影响系统性能。

对于式(6)，其波特图如图3所示，由图可见，较大的k值，带宽较大，系统的响应较快，但对基频的选通性降低，滤波性能下降。

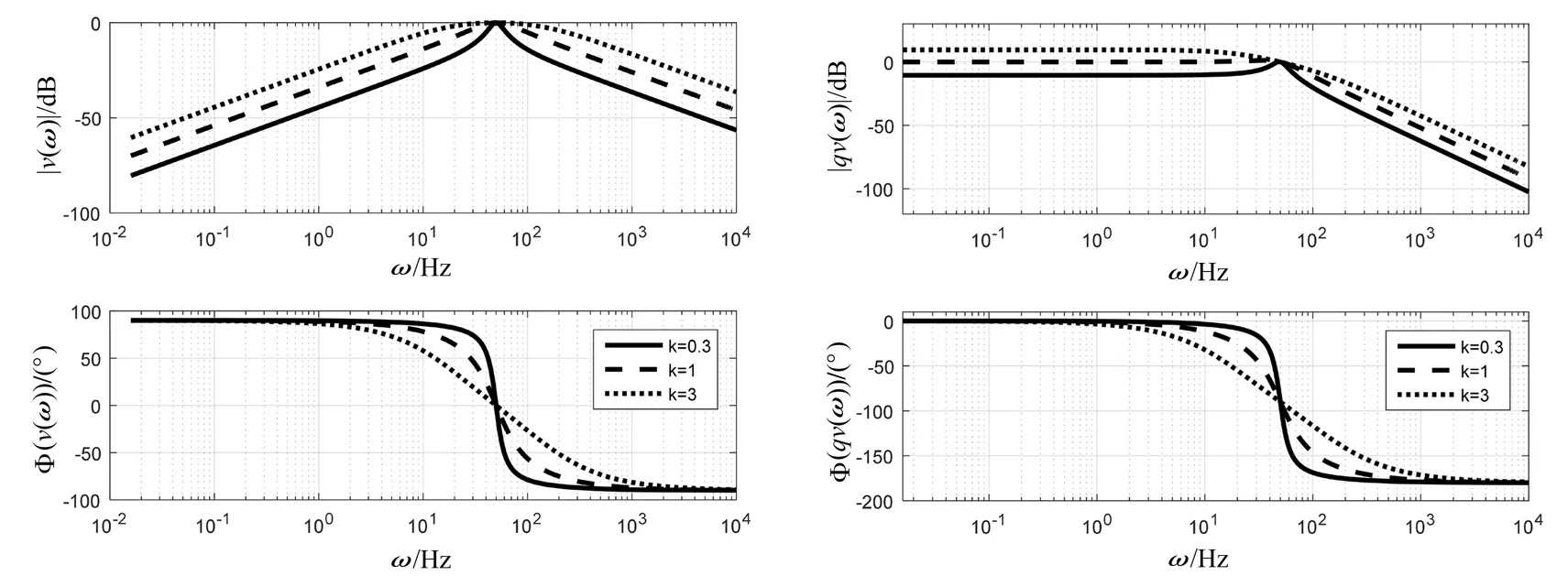
图3 不同k值时Hd(s) Hq(s)的波特图

对于式(7)，波特图如图5所示，可以看出，基频ω处相位总是滞后90°，放大倍数为1，且较大的k值对基频处的频率变化扰动有较好的适应性，但对输入信号低频抑制能力减弱[5]。

3 闭环系统参数设计

SRF-PLL的近似线性化模型可用图4表示，环路滤波器采用PI调节器形式，即：

(8)

其中Kp和τ分别是PI调节器比例增益和积分常数。

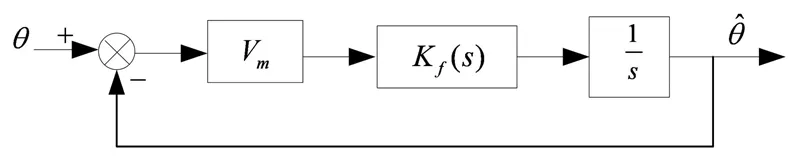
图4 控制模型

开环传递函数为：

(9)

相应的闭环传递函数为：

(10)

将式(8)代入式(10)，有：

(11)

式(11)是一个典型闭环二阶系统，其标准形式为：

(12)

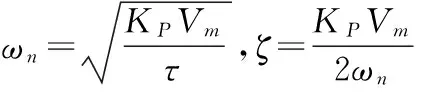
4 实验验证

以TI公司的浮点型DSP F28335为核心，在CCS开发环境下，采用C语言编写了软件实现该锁相算法。信号发生器模拟电网电压，经调理后送入F28335的12位AD模块进行转换，通用定时器产生频率为10 kHz的采样脉冲驱动中断程序运行，锁相算法每0.000 1 s运行一次。软件中运算变量数据调制在载频为150 kHz的PWM波向GPIO口输出，外接截止频率600 Hz低通RC滤波后，实时观测[6]。对于三角函数运算，软件中加入经TI公司优化后的浮点运算库，直接调用实时计算。积分运算采用后向欧拉方法实现离散化，为了减小高速运算中的累计误差，PI调节器采用增量式结构，测试表明乘法和加法的速度足够快，但应避免耗时较多的除法运算。本文取k=1，Kp=0.65，τ=2.32×10-3。

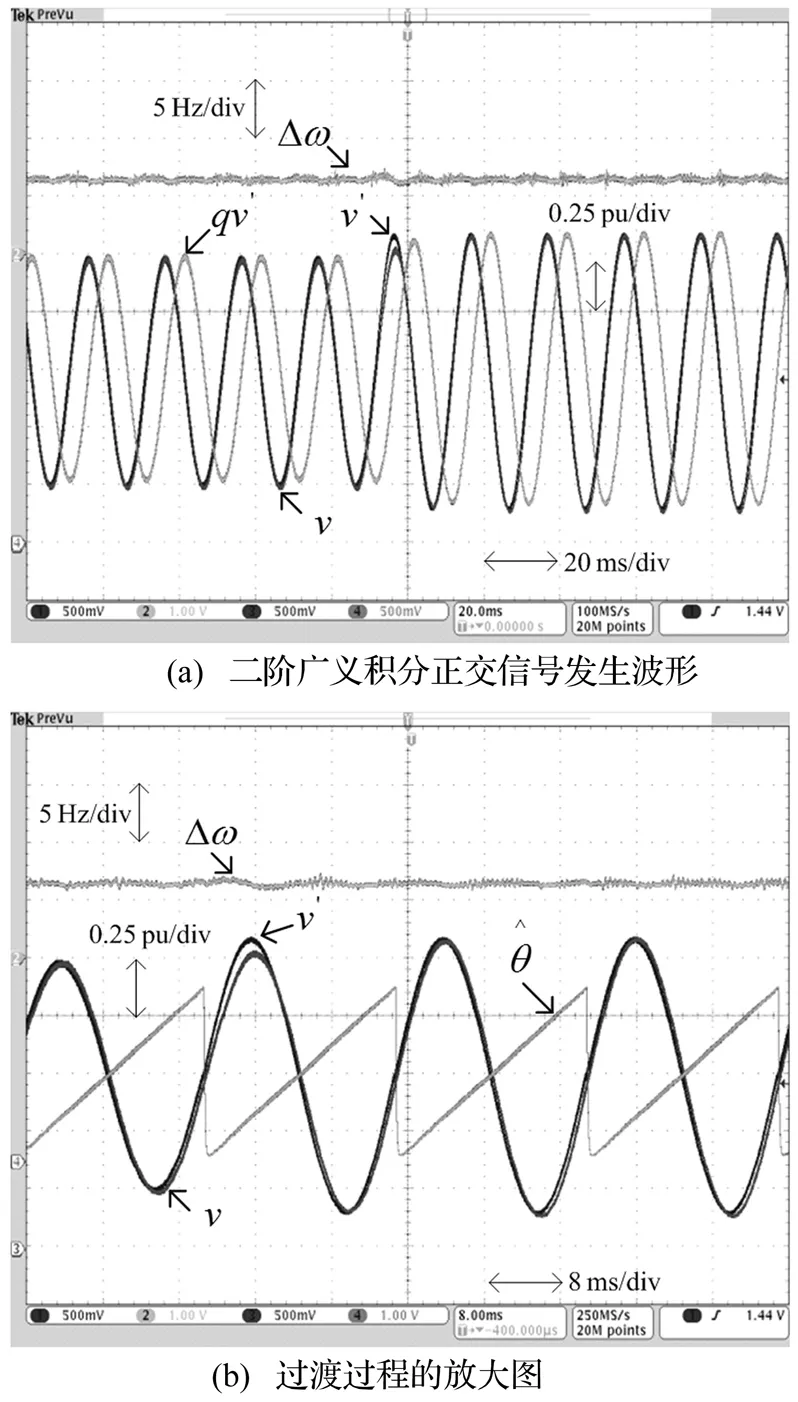
图5 电网电压幅值突增20%情况下的响应

图5给出了电网电压幅值突增20%情况下的响应，图6给出了电网电压幅值突降低20%情况下的响应，频率信号曲线为实际频率和观测频率的差值，可以看出二阶广义积分正交信号发生器响应较快，基本无延时，过渡过程的放大图表明系统可以很好的实现对v的锁相，且耗时不足1个周期，速度很快。

图7给出了电网电压频率从50 Hz突变至55 Hz情况下的响应，系统锁相效果良好，过渡过程耗时约2个周期，最大频率偏差只有4 Hz。

图8给出了电网电压叠加了30%的3次谐波、50%的5次谐波、70%的7次谐波情况下的响应，由于电网电压波形畸变严重，畸变严重的v和正交信号qv′后续锁相效果有影响。

5 结束语

本文结果表明：(1)SIGO方法的动态性能依赖于参数k和ω，当电网电压的频率偏离额定值后，该方法的选频性能下降，正交信号的生成质量会恶化，进而会影响后续SFR。通过实时观测输入电网电压的频率，使得SIGO的传递函数自适应频率变化，能提高正交信号发生器的动态性能。(2)当环路滤波器采用PI形式时，利用二阶最佳原则整定，且选择参数值不唯一，在较宽范围内都能满足系统的稳定性与快速性，在工程中十分便利。(3)该方法易于数字化实现，运算密度适中，利用高速DSP实现该算法时，针对本文的实验平台采样周期为1/10 kHz，通过适当的优化乘法和加法运算，算法执行约50个机器周期，占中断函数执行时间的比例为3%，剩余时间执行变流设备的其它核心控制程序。(4)当电网电压的发生严重的波形畸变后，由于正交信号构造环节的性能受到影响，锁相质量变差，可通过提取基波信号的方法滤波予以改善。

图7 电网电压频率从50 Hz突变至55 Hz情况下的响应

图8 电网电压谐波情况下的响应

[1] CHUNG S K. A phase tracking system for three phase utility interface inverters[J]. IEEE Transactions on Power Electronics, 2000, 15(3):431-438.

[2] 龚锦霞，解大，张延迟．三相数字锁相环的原理及性能[J]．电工技术学报，2009，24(10)：94-99．

[3] MIHAI CIOBOTARU, REMUS TEODORESCU, FREDE BLAABJERG, et al. A new single-phase PLL structure based on second order generalized integrator[C]. IEEE Power Electronics Specialists Conference,2006.

[4] 薛尚青，蔡金锭．基于二阶广义积分器的基波正负序分量检测方法[J]．电力自动化设备，2011，24(11)：69-73．

[5] 祁新梅,沈海滨,余文海,等. 基于二阶广义积分单相锁相环的改进及实现[J]. 电力电子技术,2016,50(1):96-98.

[6] D M ALTER.Using PWM output as a digital-to-analog converter on a TMS320F280X digital signal controller[C].Texas Instruments Application Report SPAA88,Feb,2006.

Experimental Research on the Phase Lock Method for Single-phase Grid Voltage Based on Second Order Generalized Integral

Xie Menxi, Shi Binwei

(Research Institute of Intelligent Structure and Systems, Suzhou University, Suzhou Jiangsu 215006, China)

Synchronization of power electronic current transformers of grid connection type is realized through accurate detection of the phase of network voltage. Synchronous reference frame approach, an excellent phase lock scheme for three-phase network voltage, constructs a virtual orthogonal signal based on the second order generalized integral to extend the synchronous reference frame approach to phase lock of single-phase networks. This paper analyzes in detail the control flow and parameter selection of this approach. The algorithm is realized on an experimental platform using DSP F28335 as control core to obtain response results in the cases of magnitude saltation and frequency discontinuity of grid voltage as well as harmonic condition. The correctness of this method is thus verified.

phase-locked loop; synchronous reference frame transformation; orthogonal signal generator; second order generalized integral (SOGI); digital signal processor; experimental research

10.3969/j.issn.1000-3886.2016.06.017

TM761

A

1000-3886(2016)06-0054-04

谢门喜(1984-)，男，甘肃甘谷人 ，专业：电气自动化技术。

定稿日期: 2016-06-16