基于混合概率的新型小波变异量子粒子群算法

胡 皞,常 军,巩文龙，刘文波

(苏州科技学院，江苏 苏州 215011)

基于混合概率的新型小波变异量子粒子群算法

胡 皞,常 军,巩文龙，刘文波

(苏州科技学院，江苏 苏州 215011)

量子粒子群算法(QPSO)具有全局寻优能力不强，且容易陷入局部最优的缺陷，因此，针对这个问题，提出了一种基于混合概率的新型小波变异量子粒子群(M-WMQPSO)算法的改进算法。该算法首先在粒子进化方程中引入高斯分布，采用混合概率分布进化方程取代标准QPSO进化方程，以此来提高算法的寻优能力。接着，为了更好地提高算法的全局寻优能力，改善算法容易陷入局部最优的缺陷，在粒子进化过程中以一定的概率对粒子进行新型小波变异处理，增加粒子种群的多样性，避免了粒子在寻优过程中陷入局部最优，从而实现算法全局寻优的目的。最后，采用六个典型测试函数对该改进算法的性能进行验证。测试结果表明，改进算法的寻优能力和避免局部最优能力都有很大提高。

量子粒子群算法；混合概率；小波；局部最优；全局最优

0 引 言

粒子群算法(Particle Swarm Optimization，PSO)[1]是一种群智能优化算法，其思想来源于对鸟群觅食过程的模拟，通过个体间的竞争与合作，产生群体智能指导优化搜索。该算法具有无需导数信息，计算简单，且易于实现等优点，可用于解决大量非线性、不可微和多峰值的复杂问题优化，因而已在软件开发、通信技术、资源分配等众多领域得到了广泛应用[2-7]。但是，由于在粒子群算法中，粒子的运动状态由速度和位置所决定，并且随着不断的演化，粒子的运动轨迹是固定不变的,同时,粒子的移动速度在演化中也会受到一定的约束，这些导致粒子的搜索范围是一个有限的并且逐渐缩小的区域，不能覆盖整个可行解空间，这就可能越过目标全局最优位置，而陷入局部最优。分析也证明PSO算法并不能以全概率1收敛到全局最优位置[8]。

于是，孙俊[9]根据量子物理基本理论，从量子力学的角度提出了一种具有量子行为的粒子群算法(Quantum-behaved Particle Swarm Optimization，QPSO)[10]。QPSO算法具有控制参数少，操作简便，能保证粒子概率1全局收敛，并且寻优性能大大优于标准PSO算法。但是，与大多数算法一样，在迭代后期由于粒子的聚集性，QPSO算法也存在早熟收敛现象。

针对这个问题，文中提出一种基于混合概率分布的,并在粒子进化过程中加入小波变异处理的改进QPSO算法。通过测试函数仿真结果表明，提出的改进算法的寻优能力和计算效率都取得了令人满意的结果，并且由于加入变异处理，算法的全局寻优能力也得到了增强，有效地避免了粒子陷入局部最优问题。

1 QPSO算法原理

在孙俊等提出的QPSO算法中，粒子的状态不再由粒子的位置和速度决定，而是通过粒子运动的波函数描述，建立δ势阱，并求解对应的定态薛定谔方程[11]，得到粒子在空间某一位置的概率密度函数，进而确定位置的分布函数，应用蒙特卡洛方法，得到粒子状态进化方程：

pi,j(t)=φj(t)·Pi,j(t)+[1-φj(t)]·Gj(t)

(1)

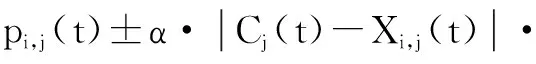
(2)

其中

(3)

式中，p为粒子在进化迭代过程中的吸引子；P为粒子当前最优值；G为粒子全局最优值；X为粒子的当前位置；C为平均最优位置；M为粒子群体数；φ和u均为(0,1)上均匀分布的随机数；参数α为压缩-扩张因子[12-13]；t为粒子当前迭代次数。

尽管量子粒子群算法的各方面性能均优于粒子群算法，但是量子粒子群算法与粒子群算法具有相同弊病，就是在迭代搜索寻优过程中全局搜索能力降低的同时群体多样性也不断减少，粒子密集堆积，搜索空间变得越来越小，粒子失去活力只会在小范围内来回徘徊，进化停滞，粒子群最终搜寻的最优解很有可能是局部最优，出现早熟的趋势。因此如何增强粒子群在进化搜索中后期的全局搜索能力，成为改进量子粒子群算法的关键。

2 基于混合概率的QPSO原理

从标准QPSO算法的粒子进化方程可以看出，原来的进化方程中使用单一的概率分布函数，现在考虑使用混合概率分布函数。一维的时候，QPSO算法的粒子进化方程为：

(4)

式中，第二项是一个双指数分布的随机项。将该式表示成更一般的形式：

X(t+1)=p(t)±A(t)

(5)

式中，A(t)为一随机序列，并且收敛到0，这样，便可以保证X(t)能依概率收敛到p(t)。QPSO算法中，A(t)是服从双指数分布的。

现将A(t)假定为以下形式：

A(t)=a(t)+b(t)

(6)

式中，a(t)和b(t)是两个服从不同概率分布的随机序列。孙俊等曾提出，令a(t)和b(t)分别服从高斯分布和双指数分布。具体地，分别规定：

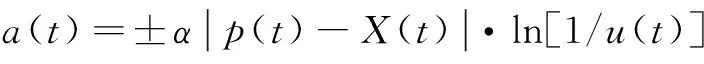
(7)

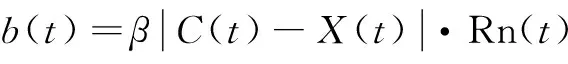
(8)

式中，u(t)服从区间(0,1)内的均匀分布；Rn(t)服从标准高斯分布；参数α和β称为收缩-扩张系数。

这样粒子的进化方程便可以写成:

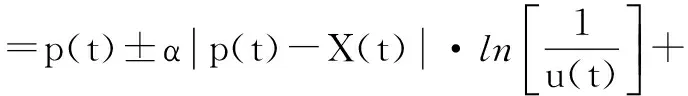
(9)

而扩展到N维搜索空间中，粒子的进化方程为:

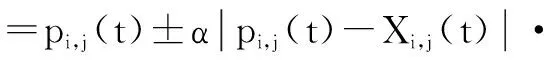
(10)

上式即为基于混合概率的QPSO算法(Mixed-probabilitybasedQuantum-behavedParticleSwarmOptimization，M-QPSO)的粒子进化方程，通过测试函数表明，M-QPSO算法提高了粒子的寻优能力，收敛速度相对于标准QPSO也得到了提高。但是同标准QPSO算法一样，算法仍容易出现早熟，粒子容易停滞在一些局部极值点，局部收敛问题仍没有得到很好的改善。

3 新型小波变异原理

由于小波具有变化幅度小、有波动的特性，微调能力强；其两个控制参数平移因子和尺度因子可以根据不同情况将小波进行平移和缩张，适应性和可变性强。LingSH等[14]将突变小波函数因子用于改进粒子群算法，提出一种混合小波变异粒子群算法。高东慧等[15]改进了突变粒子的吸引中心，提出一种改进小波变异粒子群算法。上述对粒子群算法的改进收到了一定效果，但依然无法避免粒子群算法自身轨道式进化，搜索空间受限的缺陷。尽管如此，小波变异改进粒子群算法为小波变异用于量子粒子群算法提供了可能。于是，文中提出一种新型小波变异方法，即利用小波变异代替收缩-扩张系数α来提高搜索进化进程中的全局搜索能力，增加粒子群的多样性，帮助粒子群跳出局部最优。

文中将采用复Morlet小波[16]实部作为变异因子，复Morlet小波函数实部的时域表达式为：

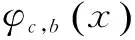
(11)

式中，c为尺度因子；b为平移因子；ω0为小波中心圆频率，一般取ω0=5。

由于变异不涉及时频转化，故令b=0，则公式(11)简化为：

(12)

定义尺度c的计算公式为：

(13)

式中，σ为c的上限最大值；τ为形状参数。

小波变异进程如下，设在每次迭代更新中每个粒子以概率q突变，q∈(0,1)，变异公式为：

(14)

式中，x取-2.5c到2.5c的均匀分布随机数，即x∈U(-2.5c,2.5c)。

小波函数的小幅值波动使得在变异公式中可以同时扮演收缩-扩张系数α和势阱δ的角色，且不定向的随机波动能增大粒子群全局搜索能力，有利于避免陷入局部最优，优化算法收敛于全局最优。

4 基于混合概率的新型小波变异量子粒子群算法

为了提高QPSO算法的寻优性能，并改善QPSO算法全局搜索能力差，容易陷入局部最优的缺陷，文中提出基于混合概率的新型小波变异量子粒子群算法(Mixed-probabilitybasedNewWaveletMutationQuantum-behavedParticleSwarmOptimization,M-WMQPSO)，也就是在采用混合概率分布进化方程替代标准QPSO进化方程的基础上，再在粒子进化过程中加入新型小波变异，以一定的概率对粒子进行变异处理。通过变异，可以改变粒子群的前进方向，使粒子进入其他新的区域进行搜索，增加粒子种群的多样性,避免粒子停留在一些局部极值点，从而增强粒子的全局搜索能力。M-WMQPSO算法的具体步骤如下：

步骤1：确定粒子种群规模M，维数D，并初始化粒子的位置；

步骤2：计算每个粒子的适应值，并更新粒子当前最优位置Pi(t)和全局最优位置G(t)；

步骤3：根据公式(10)更新每个粒子的位置，产生新的粒子种群；

步骤4：生成随机数r∈(0,1)，若r

步骤5:判断算法是否满足最大迭代数，若没有返回步骤2；

步骤6：输出全局最优位置G，算法结束。

5 测试函数分析

文中分别使用Sphere函数、Rosenbrock函数、Griewank函数、Ackley函数、Schwefel函数、Ellipse函数这六个具有代表性的测试函数进行测试(见图1)。仿真中，采用种群规模20，维数分别取10，最大迭代次数为1 000，标准QPSO中收缩-扩张因子α的值随迭代次数从1.0到0.5线性减小。对于M-WMQPSO中，参数α固定为0.6，参数β随迭代次数从0.9到0.4线性减小，形状参数τ取值为5，突变概率q设为0.05，σ取值为100 000。

分别运用标准QPSO算法、M-QPSO算法、WMQPSO算法和M-WMQPSO算法进行测试，粒子位置的搜索区间与初始化区间见表1，具体测试结果见表2。

文中所选测试函数中，Sphere函数为一非线性且图像对称的单峰函数，主要用与检验算法的寻优精度；Rosenbrock函数、Schwefel函数和Ellipse函数主要用于检验算法的寻优能力；Griewank函数和Ackley函数都为多峰函数，具有大量的局部最优点，所以算法很容易陷入局部最优，所以一般用于检验算法抵抗局部最优能力[17]。

从上述测试函数运算结果和算法的寻优曲线可以看出，M-WMQPSO算法的识别结果明显优于标准QPSO算法、M-QPSO算法和WMQPSO算法。特别Griewank函数和Ackley函数两个多峰函数的测试结果明显优于其他算法，这说明改进算法的跳出局部最优能力得到了很大提高。而其余测试函数的结果也表明，M-WMQPSO算法的寻优性能和收敛精度也是最好的，因此，M-WMQPSO算法的性能均较QPSO算法、M-QPSO算法和WMQPSO算法有所改进。

6 结束语

文中在标准QPSO算法的基础上，首先对进化方程进行改进，引入高斯变量，使QPSO算法进化方程从基于单一概率分布改进为基于混合概率分布，改进后算法的寻优性能得到了提高。

表1 测试函数相关信息

表2 测试函数的测试结果

图1 测试函数寻优曲线

针对算法容易陷入局部最优的问题，接下来利用小波变异代替收缩-扩张系数α得到变异公式，在进化过程中，根据一定的概率，对粒子进行变异，通过改变粒子群的前进方向，使粒子进入其他新的区域进行搜索，避免粒子停留在一些局部极值点，从而提高搜索进化进程中的全局搜索能力，增加粒子种群的多样性，帮助粒子群中陷入局部最优的粒子跳出局部最优。

通过典型测试函数的仿真结果分析表明，M-WMQPSO算法的寻优性能和避免局部最优能力都得到了提高，因此基于混合概率分布和小波变异的改进方法是有效的。

M-WMQPSO算法的不足之处是，由于加入了小波变异处理，这使得算法的控制参数过多，如何减少控制参数可成为进一步改进该算法的一个目标。

[1]KennedyJ,EberhartRC.Particleswarmoptimization[C]//ProceedingsofIEEEinternationalconferenceonneuralnetworks.[s.l.]:IEEE,1995:1942-1948.

[2] 温 涛，盛国军，郭 权,等.基于改进粒子群算法的Web服务组合[J].计算机学报，2013,36(5):1031-1046.

[3] 温 勇，王 美.基于粒子群算法的无线传感网络部署的研究[J].计算机技术与发展，2013,23(4):202-205.

[4] 田宏伟，解 福，倪俊敏.云计算环境下基于粒子群算法的资源分配策略[J].计算机技术与发展,2011,21(12):22-25.

[5] 潘丽姣,吴红英.混沌逃逸粒子群优化算法在WSN覆盖优化中的应用[J].重庆邮电大学学报:自然科学版,2014,26(2):177-181.

[6] 顾晓燕,孙力娟,郭剑,肖甫.一种有向传感器网络改进粒子群覆盖增强算法[J].重庆邮电大学学报:自然科学版,2011,23(2):214-219.

[7] 梁正友，支成秀．基于离散粒子群优化算法的网格资源分配研究[J]．计算机工程与科学，2007, 29(10) 77-78.

[8]ClercM,KennedyJ.Theparticleswarm-explosion,stability,andconvergenceinamultidimensionalcomplexspace[J].IEEETransactionsonEvolutionaryComputation,2002,6(1):58-73.

[9] 孙 俊.量子行为粒子群优化算法研究[D].无锡：江南大学,2009.

[10]YangSY,WangM,JiaoLC.Aquantumparticleswarmoptimization[C]//ProcofIEEEcongressonevolutionarycomputation.Portland,OR,US:IEEEPress,2004:320-324.

[11]SchrödingerE.Anadulatorytheoryofthemechanicsofatomsandmolecules[J].PhysRev,1926,28(6):1049-1070.

[12]ShiYH,EberhartRC.Amodifiedparticleswarmoptimizer[C]//ProceedingsoftheIEEEinternationalconferenceonevolutionarycomputation.Piscataway,NJ:IEEEPress,1998:69-73.

[13]ShiYH,EberhartRC.Fuzzyadaptiveparticleswarmoptimization[C]//Procofcongressonevolutionarycomputation.Seoul,Korea:IEEEServiceCenter,2001:101-106.

[14]LingSH,IuHHC,ChanKY,etal.Hybridparticleswarmoptimizationwithwaveletmutationanditsindustrialapplications[J].IEEETransactionsonSystems,ManandCybernetics,PartB:Cybernetics,2008,38(3):743-763.

[15] 高东慧,董平平,田雨波,等.一种改进的小波变异粒子群优化算法[J].计算机工程,2012,38(21):145-147.

[16] 罗光坤.Morlet小波变换理论与应用研究及软件实现[D].南京：南京航空航天大学，2007.

[17] 丁 颖.量子粒子群算法的改进及其在认知无线电频谱分配中的应用[D].南京：南京邮电大学，2013.

A New Particle Swarm Optimization Algorithm of Wavelet Mutation Quantum-behaved Based on Mixed-probability

HU Hao,CHANG Jun,GONG Wen-long,LIU Wen-bo

(Suzhou University of Science and Technology,Suzhou 215011，China)

Quantum-behaved Particle Swarm Optimization (QPSO) algorithm has defects that the capability of global optimization is not strong and is easy to fall into the local optimum.To solve this problem,an improved quantum-behaved particle swarm optimization is presented by introducing Gaussian distribution into the evolution equation,and the evolution equation of QPSO is substituted by mixed probability distribution evolution equation,and some particles were mutated in a definite probability by wavelet during evolution to increase the diversity of the particle population,avoiding the optimization process into local optimization,and improve the capability of global optimization.Finally,six typical test functions are employed to verify the improved method.The results show that the optimization capability and the ability to avoid local optimum of improved algorithm have been improved effectively.

quantum-behaved particle swarm optimization;mixed probability;wavelet;local optimization;global optimization

2015-04-07

2015-07-10

时间：2016-01-04

江苏省自然科学基金项目(BK20141180)；江苏省结构工程重点实验室开放课题(ZD1405)

胡 皞(1989-)，男，硕士研究生，研究方向为桥梁健康监测、人工智能优化算法；常 军，博士，硕士生导师,研究方向为桥梁健康监测、智能优化技术。

http://www.cnki.net/kcms/detail/61.1450.TP.20160104.1505.030.html

TP301

A

1673-629X(2016)01-0078-04

10.3969/j.issn.1673-629X.2016.01.016