基于Memetic算法的多目标复杂网络社区检测
周春霞,周井泉,常瑞云
(南京邮电大学 电子科学与工程学院,江苏 南京 210003)
基于Memetic算法的多目标复杂网络社区检测
周春霞,周井泉,常瑞云
(南京邮电大学 电子科学与工程学院,江苏 南京 210003)
文中研究复杂网络社区检测机制,提出了一种基于Memetic算法的多目标社区检测算法。为了提高种群多样性、减少搜索空间和提高算法效率,算法采用标签启发式快速传播的初始化策略,混合交叉,在每个社区中选择一个节点变异等优化两个目标函数,即Improved Ratio Association (IRA)和Ratio Cut (RC),将多目标优化问题转化成同时最小优化这两个目标函数;在局部搜索中利用权重和将两个目标函数构成一个局部优化目标并采用爬山搜索来寻找个体最优。针对计算机合成网络与两个经典真实网络的实验结果表明,与四个基于EA的算法和Fast modularity算法相比,基于Memetic算法的多目标复杂网络社区检测机制在解决复杂网络社区检测问题上具有一定优势。
Memetic算法;混合交叉;局部搜索;多目标;网络社区检测
1 概 述
由于许多复杂的系统包括协作网络[1]、万维网[2]等都可以建模为复杂网络。因此,近年来复杂网络成为人们的关注热点。除了许多显著的性质,如小世界性、无尺度性和高聚类系数外,社区结构是复杂网络的另一个重要属性,它将一个复杂网络分成不同的分区,每一个这样的分区称为一个社区[3]。定性来看,社区的定义是网络中一些节点的集合,这些节点以相互连接的模式存在,在同一分区的节点间联系密切,不在同一分区的节点间联系比较稀疏,属于同一社区的节点通常来说会有相同的属性[4]。因此在复杂网络中进行社区检测非常必要。
到目前为止,已经开发了许多网络社区检测的算法。
一类是基于启发式的,这类算法通过基于某些直观的假设或启发式规则来找到网络的各个社区,如Girvan-Newman (GN)算法[3],快速的标签传播算法(LPA)[5]等。GN算法不断地从网络中移除介数最大的边,直到网络中所有的边都被移除。边介数定义为网络中经过每条边的最短路径数目,算法弥补了一些传统算法的不足,能够从网络的拓扑结构进行分析;LPA算法首先为每个节点指派唯一标签,再将每个节点的标签更新为其邻节点出现次数最多的标签,如果存在多个相同的最多标签,则随机选择一个作为更新值,若干次迭代后密集相连的节点会收敛于同一标签,最终,具有相同标签的节点归为一个社区。LPA算法的优点在于不需要任何参数输入,而且算法具有线性的时间复杂度为O(m),m为网络的边数。
另一类是基于模块度的优化算法,Newman等通过引入一个衡量网络划分质量的指标:标准模块度(Q)[3],依据Q值评价网络社区划分的优劣,从而将社区检测转化为一个优化问题。典型的算法有Newman快速算法[6]、Fastmodularity算法[7]等。Newman快速算法将每个节点看作是一个社区,每次迭代选择产生最大Q值的两个社区合并,直至整个网络融合成一个社区;Fastmodularity算法的基本思想是用贪婪优化算法优化模块度这个目标函数,得到最大的模块度值即找到了最优的网络社团划分。
然而,Fortunato和Barthelemy在文献[8]中指出以标准模块度优化的算法存在分辨率限制的问题。为了克服这个问题,Pizzuti在文献[9]中提出以社团得分(CS)为目标函数来检测网络划分的算法GA-net。Li等引入了模块度密度作为指标函数,通过调节参数能从不同分辨率分析网络拓扑结构[10]。但是研究者往往想到将多目标优化引用到复杂网络的社区结构检测中。与单目标优化问题不同的是,多目标优化问题需要同时优化多个目标函数,通常没有单一的全局最优解,而是一系列互不支配的解,称为Pareto解,多目标优化算法的目的正是寻找出一系列互不支配的解[1]。进化算法通过种群中代与代之间相关联的解来实现全局搜索,对于搜索多目标优化问题的Pareto最优解集非常有效。最近提出的多目标进化社区检测方法有MOGA-net[11]、MOCD[12]和MOEA/D-net[13]等。
Memetic算法是在种群的全局搜索基础上再对个体进行局部搜索,实际上,Memetic算法提出的是一种框架,在这个框架下,采用不同的搜索策略可以构成不同的Memetic算法。如全局搜索策略可以采用遗传算法、免疫算法等,局部搜索策略可以采用爬山搜索、模拟退火、贪婪算法、禁忌搜索、导引式局部搜索等。
文中提出了一种基于Memetic算法的多目标复杂网络社区检测机制(MOME),全局搜索中采用遗传算法框架;在局部搜索中利用权重和将两个目标函数折合成一个目标并采用爬山搜索来寻找个体最优。在遗传框架中采用标签启发式快速传播的初始化方式、个体统一标签后的混合交叉和针对社区检测的变异策略,将MOME算法运用在计算机合成网络与两个经典真实网络,并同时与四个基于EA的算法和Fastmodularity算法进行比较,其在社区检测方面更具有竞争力、准确性更高。
2 基于Memetic算法的多目标复杂网络社区检测
2.1 社区的定义

社区指网络中存在的节点子集,该子集的内部节点之间具有相对紧密的连接,子集内部节点与外部节点具有相对稀疏的连接。Radicchi等在文献[14]中基于节点度的概念给出了社区结构的定性描述:若S是网络G的一个社区,那么S中节点i的度为其内度与外度之和。其中内度是节点i与内其余节点连接的总数,外度是节点i与以外节点连接的总数,可表示为:
(1)
2.2 目标函数
Newman等在2002年引进了一个衡量网络划分质量的标准模块度(Q)[3],将网络社区检测转化为一个优化问题,Q的定义如下:
(2)

然而,Fortunato和Barthelemy在文献[8]中指出模块度优化存在分辨率限制问题,其主要原因是模块度中不在一个社区中包含社区中节点总数的信息。为解决这个主要问题,Li等在文献[10]中引入了新的指标函数:模块度密度(D)。
(3)
式中,第一个求和项表示子图节点的内度之和与该子图的节点数的比值,等价于RatioAssociation(RA)[15];第二个求和项表示子图节点的外度之和与该子图的节点数的比值,等价于RatioCut(RC)[16]。
从定义知,D值越大,找到的社区划分就越准确。即RA越大,社区内节点间的连接越密切,RC越小社区间节点间的连接越稀疏。这两个互补的项反映了一个好社区的两个基本方面,社团内连接是密切的而社区间的联系是稀疏的。
文中为了把社区检测转化成最小多目标优化问题,对RA做了修正,提出了ImprovedRatioAssociation(IRA),定义为:
(4)
其中,σ为一实数(文中取值为5)。
通过最小化IRA和RC这两个目标函数可以确保社区内连接是密切的而社区间的联系是稀疏的。
(5)
2.3 算法描述
2.3.1 编码方式
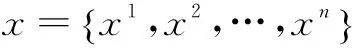
2.3.2 种群的初始化
开始时每个节点被放到一个不同的社区中,即xi=i,为了避免所有个体的标签都是这样,同时提高种群的多样性,文中采用了基于标签传播的初始化机制。首先初始化每个节点具有不同的标签,即xi=i;第二步每个节点再基于与其有边连接关系的邻居节点标签更改其自身的标签,在这次更改中每个节点的新标签是它邻居节点标签中数量最多的,若邻居节点标签都不一致,那随机选择一个来更改;最后一步是将这个过程反复进行5次。
这样紧密连接的节点通过标签传播,可以迅速形成一个共同的独特的标签,创造的个体具有较高的聚类精度,同时丰富了种群多样性。
2.3.3 交叉和变异
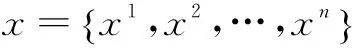
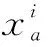
这种混合交叉操作既体现了继承性,又同样具有探索性,使产生的子代个体能够携带两个父代个体的共同特征。
变异:在变异中,首先根据个体上节点的标签得到社区结构,其次在每一个社区中随机选择一个节点,然后将这个节点的标签随机地变为其任意邻居节点的标签。这种变异操作只考虑待变异节点的邻居节点,操作相对简单,同时又能够将每一个社区考虑在内,缩小了搜索空间,减少了无效搜索,提高了算法效率。
2.3.4 局部搜索
Memetic算法框架是由种群的全局搜索和个体的局部启发式搜索结合而成,其搜索效率在一些领域比传统遗传算法快几个数量级,并且能够克服传统遗传算法收敛速度慢、容易陷入局部最优的缺点。局部搜索是在种群进行全局搜索后的基础上进行,但是并不是种群中的所有个体都进行局部搜索,在单目标中选择遗传操作后适应度值最大的个体进行,以适应度的值作为局部优化函数,直到寻找到一个局部最优的个体,在多目标中首先要确定一个局部优化函数将多个目标通过某种方式结合在一起,并且将遗传操作后的Pareto解作为局部搜索对象,通过局部搜索产生Pareto最优解。
文中全局搜索采用了遗传算法的框架,在局部搜索策略中选择采用爬山法。爬山法是一种常用于局部搜索的优化方法,通常从问题当前的一个任意解出发,试图通过改变这个解的某个元素来寻求更好解,一旦这个变化产生了一个更好的解,那么这个新解就替代被选择出来的解,这个过程一直重复直到没有更好的解产生或者达到最大的搜索次数为止,此时的解就是一个局部最优解。
MOME中多目标优化算法的局部搜索采用权重和的方式将两个不同的目标函数构成局部搜索的优化函数,如式(6):
(6)
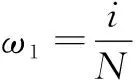
局部搜索策略中选择爬山搜索,一旦搜索出比当前优化函数值小的解就将搜索出的解代替当前解,这个过程一直重复直到没有更好的解产生或者达到最大的搜索次数为止,将对应的解作为当前代社区检测的最优解。
3 实验研究
本节将MOME应用于计算机合成网络与已知真实划分的两个真实世界网络,并且分别与不同算法得到的检测结果进行了比较。实验中使用由LeonDanon等提出的评价指标函数NormalizedMutualInformation(NMI)[17]作为相似性度量,用来衡量算法检测的结果与真实的网络划分之间的相似度。实验结果表明,MOME算法能够有效地检测出网络的社区结构,发现网络社区的层次结构,同时具有多分辨能力。
3.1 人工合成网络
使用Lancichinetti提出的基准测试网络[18]。该网络包含128个节点,4个社区,每个社区有32个节点,节点的平均度为16,混合参数μ控制节点外度所占的比例,μ越大,节点和其社区外节点的连接比例越大,社区结构越模糊。实验中调节μ的值,生成μ从0到0.5变化(间隔为0.05)的11个网络,并且使用NMI衡量真实网络划分和检测结果之间的相似性。针对个网络,计算30次独立运行结果中最大的NMI的平均值,图1给出了实验结果。
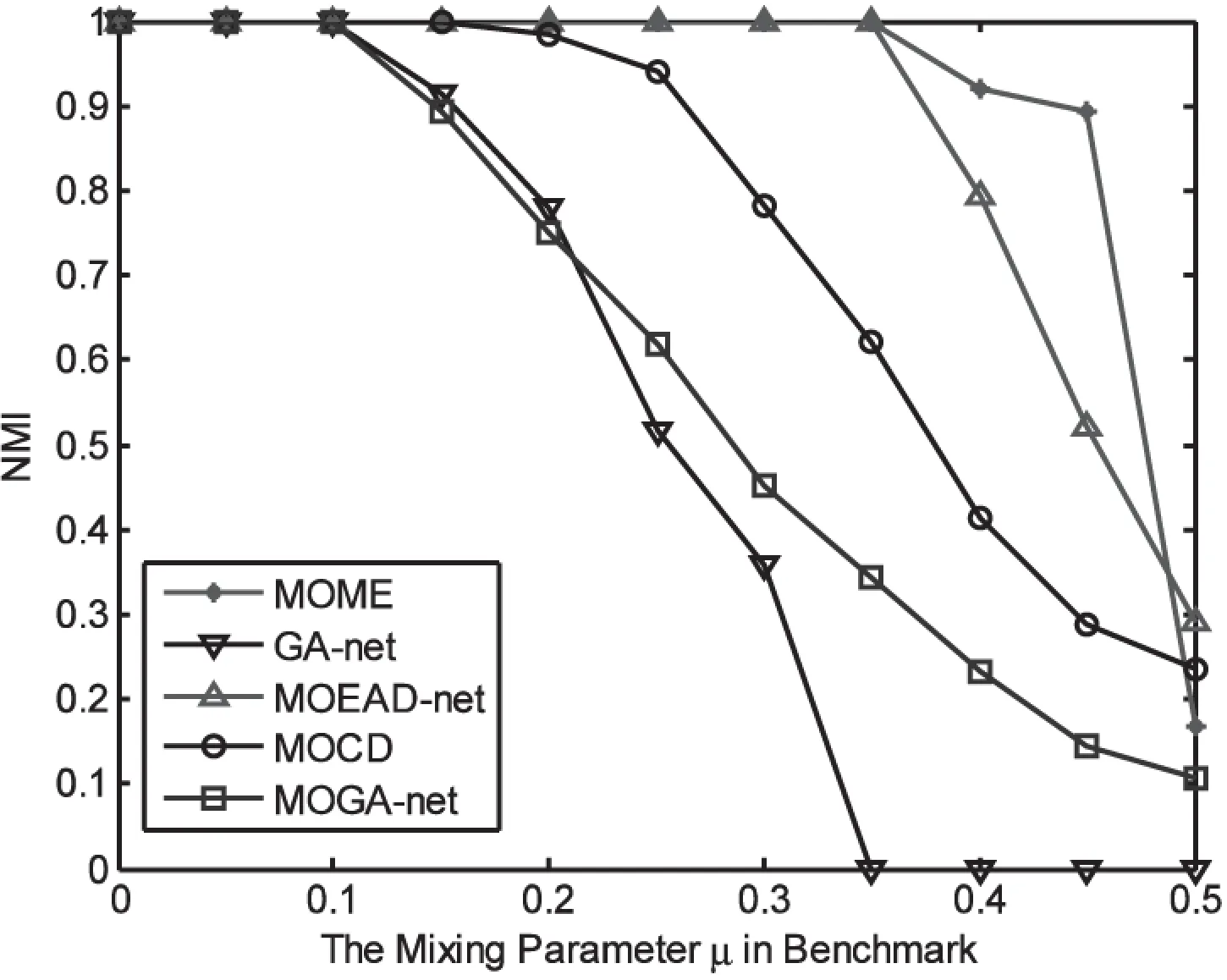
图1 5种不同算法在人工合成的 11个网络上得到的NMI的值
从图中可以看出,当混合参数μ<0.35时,代表社区结构比较明显,MOME算法能够发现网络的真实划分(NMI值为1),很明显结果优于GA-net、MOGA-net和MOCD算法;随着混合参数逐渐增大,网络的社团结构越来越模糊,寻找到真实的社区结构变得越来越困难,取0.35<μ<0.45,虽然完全检测出真实的划分变得有些困难,但NMI的值依然会高于0.85,相比其他算法的优势还是很明显;当再增大时,社团结构变得更模糊,检测出真实的划分变得十分困难,例如,对于混合参数μ=0.5的网络,网络社团结构很模糊,任何算法都很难检测出网络的真实划分。这个实验说明MOME算法能够发现有效的网络社区结构信息。
3.2 真实的网络
将MOME算法应用到两个真实的世界网络上,分别是Zachary空手道俱乐部网络[19]和美国大学足球联赛网络[3],并与Fast modularity算法得到的检测结果进行了比较。
Zachary空手道俱乐部网络是Zachary在两年时间内通过观察一个34个成员的空手道俱乐部得到的[19]。图2(a)记录Karate Club真实的社区划分结果,图2(b)表明了MOME算法在Karate Club上的社区检测结果。
从图2(b)中可以清楚地看到,MOME算法能够完全正确地检测出Karate Club的社区划分结果(对应的NMI=1),同时也显示了最高的Q值对应的社区结构,很明显图2(b)中右图为左图的子图。
美国大学足球联赛网络是Girvan和Newman编译的2000年秋季美国IA部大学足球联赛常规赛季比赛网络[3]。图3(a)记录了Football的真实社区划分结果,图3(b)表明了MOME算法在Football上检测结果。
由于网络本身存在复杂的网络结构,很难有一种算法能够完整地检测出其真实的社区划分。从图3(b)最大Q值的检测结果来看,MOME算法产生了10个社区,通过观察发现错误地放置了一些节点,如:12,25,29,37,43,51,59,60,64,70,81,83,91,98,111。然而从图3(b)NMI最大值为0.927 3来看,MOME算法依然是有效的。
为了比较,表1中列出了MOME算法和Fastmodularity算法[7]在这两个网络上独立运行30次得到的平均NMI的值。

表1 MOME算法和Fast modularity算法对网络检测的结果

图2 检测结果(1)
从表中可以看到,对于Zachary空手道俱乐部网络,MOME算法能够完整地检测出网络的真实划分,而Fastmodularity算法检测出的解对应的NMI值为0.693,显然MOME算法要优于Fastmodularity算法;对于美国大学足球联赛网络,由于网络本身结构的复杂性,两种算法都不能够完全检测出其真实的划分结果。但从表中对比可以得到,MOME算法在NMI的取值上高于Fastmodularity算法,检测到的社区结构更接近于网络的真实社区结构。通过和Fastmodularity算法的比较,可以发现MOME算法在解决复杂网络社团检测问题上更精确。
通过以上实验得出MOME算法在社区检测问题上的有效性,其检测结果也要优于基于EA算法的其他方法,与常见的检测算法如Fastmodularity算法相比,结果同样具有竞争力。
4 结束语
文中提出了MOME算法,该算法基于快速标签传播算法设计了标签启发式传播的初始化策略,提高了种群多样性;在交叉中采用对所有个体统一标签后的混合交叉策略;变异中在每个社区中选择一个节点进行变异,提高算法效率;最后通过优化IRA和RC两个目标函数来寻找Pareto解。在局部搜索中利用权重和将两个目标函数构成一个局部优化目标并采用爬山搜索策略来搜寻个体最优。
在人工合成网络和真实的世界网络上的实验结果表明,MOME算法比传统的基于EA的算法在社区检测方面更具有竞争力,与当前比较流行的Fastmodularity算法比较的结果显示,MOME算法的准确性更高。所以基于Memetic算法的多目标复杂网络社区检测机制在解决复杂网络社区检测问题上具有一定优势。
[1]NewmanMEJ.Thestructureofscientificcollaborationnetworks[J].ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica,2001,98:404-409.
[2]BroderA,KumarR,MaghoulF,etal.GraphstructureintheWeb[J].ComputerNetworks,2000,33:309-320.
[3]GirvanM,NewmanMEJ.Communitystructureinsocialandbiologicalnetworks[J].ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica,2002,99:7821-7826.
[4]FortunatoS.Communitydetectioningraphs[J].PhysicsReports-ReviewSectionofPhysicsLetters,2010,486:75-174.
[5]RaghavanUN,AlbertR,KumaraS.Nearlineartimealgorithmtodetectcommunitystructuresinlarge-scalenetworks[J].PhysRevE,2007,76(3):036106.
[6]NewmanMEJ.Fastalgorithmfordetectingcommunitystructureinnetworks[J].PhysicalReviewE,2004,69:066133.
[7]ClausetA.Findinglocalcommunitystructureinnetworks[J].
Physical Review E,2005,72:026132.
[8] Fortunato S,Barthelemy M.Resolution limit in community detection[J].Proceedings of the National Academy of Sciences of the United States of America,2007,104:36-41.
[9] Pizzuti C.GA-Net:a genetic algorithm for community detection in social networks[C]//Proc of PPSN X.[s.l.]:[s.n.],2008:1081-1090.
[10] Li Z,Zhang S,Wang R S,et al.Quantitative function for community detection[J].Physical Review E - Statistical,Nonlinear,and Soft Matter Physics,2008,77:036109.
[11] Pizzuti C.A multiobjective genetic algorithm to find communities in complex networks[J].IEEE Transactions on Evolutionary Computation,2012,16(3):418-430.
[12] Shi C,Yan Z,Cai Y,et al.Multi-objective community detection in complex networks[J].Applied Soft Computing,2012,12(2):850-859.
[13] Gong M,Ma L,Zhang Q,et al.Community detection in networks by using multiobjective evolutionary algorithm with decomposition[J].Physica a-Statistical Mechanics and Its Applications,2012,391:4050-4060.
[14] Radicchi F,Castellano F,Ceccon I,et al.Defining and identifying communities in networks[J].Proceedings of the National Academy of Sciences of the United States of America,2004,101(9):2658-2663.
[15] Angelini L,Boccaletti S,Marinazzo D,et al.Identification of network modules by optimization of ratio association[J].Chaos,2007,17:023114.
[16] Wei Y C,Cheng C K.Ratio cut partitioning for hierarchical designs[J].IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems,1991,10(7):911-921.
[17] Wu F,Huberman B A.Finding communities in linear time:a physics approach[J].The European Physical Journal B-Condensed Matter and Complex Systems,2004,38:331-338.
[18] Lancichinetti A,Fortunato S,Radicchi F.Benchmark graphs for testing community detection algorithms[J].Physical Review E,2008,78:046110.
[19] Zachary W W.An information flow model for conflict and fission in small groups[J].J Anthropol Res,1977,33:452-473.
Multi-objective Complex Network Community Detection Based on Memetic Algorithm
ZHOU Chun-xia,ZHOU Jing-quan,CHANG Rui-yun
(College of Electronic Science and Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
The complex network community detection mechanism was studied and a multi-objective community detection based on Memetic algorithm was presented.In order to improve the diversity of the population,reduce the search space and raise the efficiency of the algorithm,the initialization strategy of label heuristic fast propagation and hybrid crossover were used in the algorithm and a node was selected in each community for mutation to optimize two objective functions,namely Improved Ratio Association (IRA) and Ratio Cut (RC),which turns the multi-objective optimization problem into minimal optimization of these two objectives at the same time.In local search,the local optimization target is constituted of weights of two objective functions and a hill-climbing strategy is used to find the best individual.Experiments on computer-generated networks and two classic real networks show that compared with four algorithms based on EAs and fast modularity algorithm,multi-objective community detection based on Memetic algorithm has certain advantages in solving complex network community detection problem.
Memetic algorithm;hybrid crossover;local search;multi-objective;network community detection
2015-04-20
2015-08-03
时间:2016-01-04
国家自然科学基金资助项目(61003237,61401225);江苏省自然科学基金(BK20140894)
周春霞(1992-),女,硕士研究生,研究方向为复杂网络的社区检测;周井泉,博士,教授,硕士生导师,研究方向为通信网络的信息管理和控制。
http://www.cnki.net/kcms/detail/61.1450.TP.20160104.1510.056.html
TP301.6
A
1673-629X(2016)01-0053-05
10.3969/j.issn.1673-629X.2016.01.011

