某汽轮机转子动力学分析
胡雯婷 刘嘉一 盛锋


【摘 要】为了获得某汽轮机转子-轴承系统的动力学特性,并验证其可靠性。采用有限元法,通过对汽轮机转子-轴承系统进行等效简化,建立了汽轮机转子-轴承系统动力学分析模型,在此模型上对汽轮机转子-轴承系统进行转子动力学分析,包括模态分析、临界转速计算以及不平衡响应分析,分析结果表明该转子-轴承系统结构临界转速安全裕度满足要求,转子系统选取的平衡量具有较小的振动幅值,转子-轴承系统设计具有合理性,并对转子-轴承系统安全运行提供了实时监测的依据。
【关键词】转子动力学;临界转速;不平衡响应
0 引言
随着现代工业的发展,汽轮机的发展非常迅速,转速越来越快,效率也得到很大的提高。当汽轮机在运转时,转子系统常常会因为发生振动而产生噪声,使转子的工作效率降低,甚至发生失稳,引发安全事故[1],因此在汽轮机的设计之前,对转子动力学进行分析研究,就具有重要的理论意义和实用价值[2]。
应用ANSYS有限元分析软件对某汽轮机转子-轴承系统进行了动力学分析,包括模态分析、临界转速计算以及不平衡响应分析。验证了其在设计上的合理性。
1 分析方法
转子动力学以转子横向振动为主要研究对象,对旋转机械转子系统的动力学特性进行研究。主要的求解方法有传递矩阵法和有限元法。本文采用有限元方法进行分析。
转子的动力平衡方程[2]为:
[M]{?譈}+([G]+[C]){?簪 }+[K]{U }={ f }(1)
式中:[M]—质量矩阵,[G]—陀螺阻尼项,[C]—阻尼矩阵,[K]—结构刚度矩阵,{?譈 }—加速度向量,{?簪 }—速度向量,{U }—位移向量。
2 转子动力学分析
2.1 计算模型
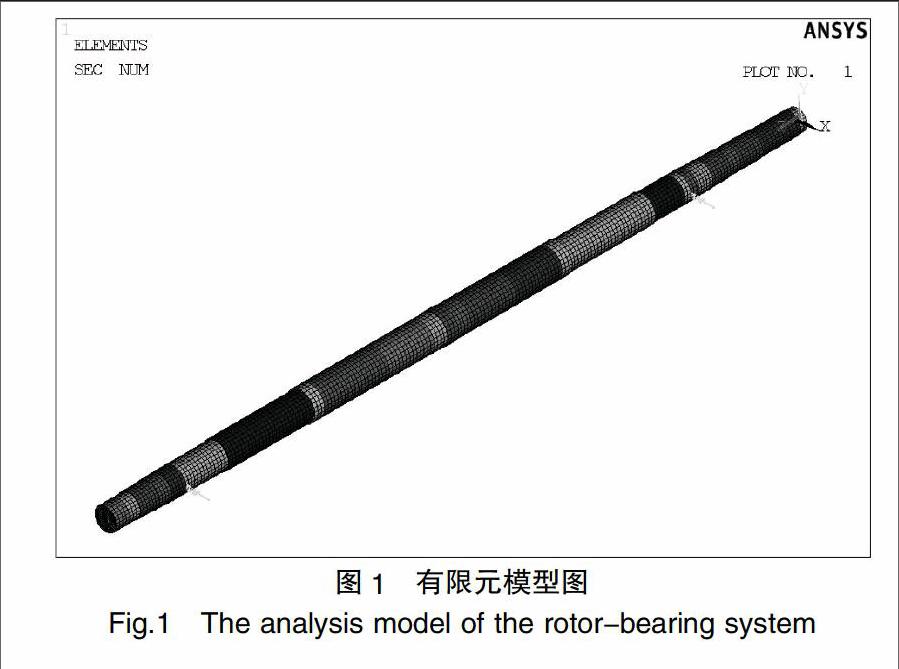
某汽轮机转子-轴承系统由主轴、叶轮和轴承组成,根据转子-轴承系统之间的关系,并按照质心不变原则,对其进行简化,将主轴、叶轮、叶片简化为阶梯转轴、圆盘和支承[3]。将主轴模拟成三维梁单元(BEAM188),叶轮模拟成质量单元(MASS21),轴承模拟成二维弹簧-阻尼单元(COMBI214)。有限元模型图见图1。
2.2 模态分析
模态分析的主要内容是研究结构或机器部件的振动特性,得到其固有频率和振型。在转子-轴承系统中,对模态进行计算,可以使设计者清晰地认识到该结构的振动特性,加以利用或控制。由于该模型弹簧单元具有阻尼,故对有限元模型进行模态分析时,选用QR阻尼法[4]进行求解。由于转子系统中叶轮转动会产生陀螺力矩,使得转子的固有频率在数值上与不计这种力矩影响时的不同。表1给出了六种不同转速下转子前六阶的固有频率值。图2~图4给出了转速为0时前三阶弯曲振型图。
由表1可知,考虑陀螺力矩影响的计算结果表明当转子做正进动时,转子固有频率随转速的增大而增大;当转子做反进动时,转子固有频率随转速的减小而减小。
2.3 临界转速计算
汽轮机转子-轴承结构比较复杂,可能由于安装条件改变、设计制造误差或大修后安装不当等原因的影响,在运行的过程中难免会存在着不平衡量,产生离心力的作用,导致汽轮机转子-轴承系统在运行的过程中发生振动,转子的振幅随转速的增大而增大,到某一转速时振幅达到最大值,超过这一转速后振幅随转速增大逐渐减少,且稳定于某一范围内,转子振幅最大时的转速称为转子的临界转速。一般在计算转子系统的临界转速时,通常只需要考虑正进动时的临界转速。对转子系统进行临界转速的分析是转子动力学很重要的部分,临界转速的求解可以使设计人员有效地规避工作转速与临界转速相差过近的风险,避免共振,提高工作的稳定性。坎贝尔图(campbell diagram),是ANSYS计算临界转速时,很直观的图形。其横轴是转子的转速,纵轴是转子的固有频率。进动频率曲线和等转速线交点对应的转速即为临界转速。转子-轴承系统的坎贝尔图见图5。
由坎贝尔图可以得到某汽轮机转子-轴承系统的一阶临界转速为2066.7rpm,二阶临界转速为9066.6rpm,转子的额定工作转速为2991rpm,高于一阶临界转速,小于二阶临界转速,故转子-轴承系统是柔性转子,其相对于一阶、二阶临界转速的裕度都大于30%,满足文献[5]关于转速偏离临界转速裕度的要求。转子-轴承系统的临界转速设计合理。
2.4 不平衡响应分析
不平衡响应分析是转子动力学分析中与临界转速计算同等重要的基本任务。不平衡响应分析也可以用来确定系统的临界转速,但是进行不平衡响应分析的一般目的是用来求解当转子系统中存在不平衡量的作用时,转子-轴承系统的振幅随转速变化的规律。按最不利的情况考虑,计算了在转子中部施加一不平衡量作为激励载荷时,两个特征位置(分别在前后轴承位置)的不平衡响应。图6为计算所得的不平衡响应曲线。
从曲线可以看出,振幅与转速呈抛物线关系,基于转速和频率的关系n=60*f,其中n为转速(rpm),f为频率(Hz),不平衡量引起的最大振幅所对应的频率与模态分析所得到的固有频率是一致的,均在34.44HZ左右,且与不平衡量大小无关;通过不平衡分析可以得到转子-轴承系统在工作转速范围内的最大响应值,在额定工作转速范围内,转子的动态响应较小,最大变形为0.038mm,可为转子-轴承系统安全运行提供实时监测的依据。
3 结论
(1)对某汽轮机转子-轴承系统进行模态分析得到不同转速下对应的频率振型图,了解了转子-轴承系统的振动情况,为转子-轴承系统结构的设计提供了重要的理论依据。
(2)转子动力学分析得到了转子-轴承系统的坎贝尔图,进而得到了转子-轴承系统前两阶正进动临界转速,通过与额定工作转速进行比较分析,结果满足设计要求,说明结构设计合理。
(3)通过不平衡响应分析得到振幅与转速呈抛物线关系,不平衡量引起的最大振幅所对应的频率与模态分析所得到的固有频率是一致的,且与不平衡量大小无关。通过稳态不平衡分析可以得到转子-轴承系统在工作转速范围内的最大响应值,可为转子-轴承系统安全运行提供实时监测的依据。
【参考文献】
[1]钟一谔,何衍宗,王正,李方泽.转子动力学[M].北京:清华大学出版社,1987.
ZHONG Yi-e,HE Yan-zong,WANG Zheng,LI Fang-ze.Rotor dynamic analysis[M].Beijing:Tsinghua university Press,1987.
[2]曾攀.有限元分析及应用[M].北京:清华大学出版社,2004.Zeng Pan. Finite element analysis and application[M].Beijing:Tsinghua university Press,2004.
[3]曾嫣,樊久铭,姚大坤.汽轮机转子动力学建模[J].电站系统工程,2007,23(4):27-28.Zeng Yan, Pan Jiu-ming, Yao Da-kun. Modeling on dynamics of Turbine rotor[J].Power station systems engineering,2007,23(4):27-28.
[4]包陈,王呼佳.ANSYS工程分析进阶实例[M].北京:中国水利水电出版社,2009.Bao Chen,Wang Hu-jia. ANSYS advanced example of engineering analysis[M].Beijing:ChinaWater Conservancy and Hydropower Press,2009.
[5]API648转子动力学通用标准[S].API RP 684, Paragraphs, Rotodynaminc Tutorial: Lateral Critical Speeds, Unbalance Response, stability, Train Torsionals and Rotor Balancing[S].
[责任编辑:王楠]

