让“恒量”搭桥巧解电学题

□

让“恒量”搭桥巧解电学题

□王伦宇

在求解电学试题时，若我们善于把“恒量”（不变物理量或相等物理量）设为参数，再利用它牵线搭桥列出等式或构建方程求解，可使解题思路清晰，运算过程简单，达到事半功倍的效果，下面结合实例分类解析.

一、让不变量——电源电压搭桥

例1（2016·崇左）如图1所示的电路中，电源电压保持不变，R1为定值电阻，R2为滑动变阻器（a、b为其两个端点）.当闭合开关S，滑片P在某一端点时，电压表示数为8V，R2消耗的功率为0.8W；当滑片P移到另一位置时，电流表示数为0.3A，R2消耗的功率比原来增加了1W.则滑动变阻器R2的最大阻值是Ω，整个电路消耗的最大功率是W.

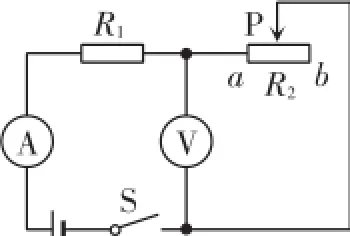
图1

解析：由图知，R1、R2串联.当闭合开关S，滑片P在某一端点时，电压表示数为8V，R2消耗的功率为0.8W，电路中电流0.1A，R1两端电压U1=I1R1=0.1A×R1.设电源电压为U，则由串联电路中U=U1+U2和欧姆定律得

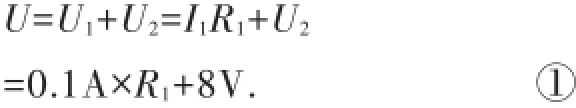
当滑片P移到另一位置时，R2两端电压R1两端电压同理得

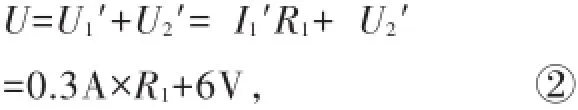
联立①、②得R1=10Ω，U=9V.

由滑片P在某一端点时R2两端电压大于滑片P移到另一位置时R2两端电压，由串联电路中电阻分压原理可知电压表示数为8V时，滑片P在端点b，故滑动变阻器R2的最大阻值当滑片P在a端时，整个电路消耗的最大功率

答案：808.1

二、让不变量——定值电阻搭桥

例2（2016·天水）如图2所示，当开关S闭合，甲、乙两表均为电压表时，两表示数之比U甲∶U乙= 3∶1；当开关S断开，甲、乙两表均为电流表时，两表示数之比I甲∶I乙=，相同时间内R1、R2产生的热量之比Q1∶Q2=.

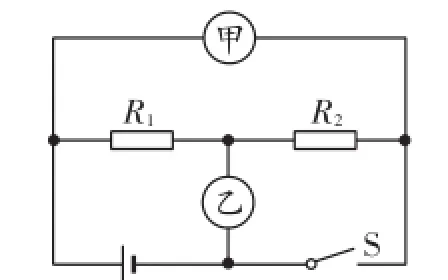
图2

解析：由图可知，当开关S闭合，甲、乙两表为电压表时，电阻R1、R2串联.设R1、R2两端电压分别为U1、U2，电路中电流为I，则根据串联电路中U总=U1+U2、欧姆定律，依题意得

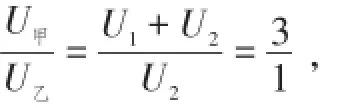
由图可知，当开关S断开，甲、乙两表为电流表时，电阻R1、R2并联，甲、乙两表分别测电阻R2和并联电路干路电流.又设通过电阻R1、R2的电流分别为I1、I2，则根据并联电路各支路两端电压相等和欧姆定律可得

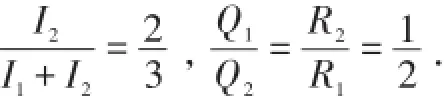
答案：2∶31∶2

三、让相等量——串联电路中的电流搭桥

例3（2016·襄阳）如图3所示，电源电压不变，灯泡L标有“4V2W”字样，R0的阻值为16Ω.当S1、S2断开、S3闭合，滑片P从b端滑到某一位置时，滑动变阻器R接入电路的电阻减小了8Ω，此过程中电压表的示数由3.2V变为4V.则：

（1）灯泡的电阻为，灯泡正常工作时的电流为A.

（2）电源电压和滑动变阻器的最大阻值各为多少？（不考虑温度对灯丝电阻的影响）

（3）当S1、S2闭合，S3断开时，电路消耗的最小功率是多少？（符合电路操作规范要求）

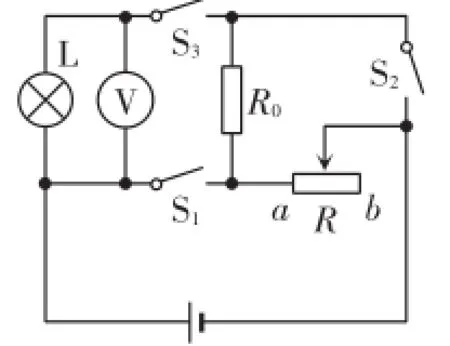
图3

解析：（1）灯泡的电阻为：

灯泡正常工作时的电流为：

（2）当S1、S2断开、S3闭合时，灯泡L、R0、滑动变阻器R串联.设滑片P在b端时，串联电路电流为I，电源电压为U，滑动变阻器接入电路的电阻为R（此时滑动变阻器接入电路的电阻最大），则根据串联电路电流处处相等和即

代入数据得

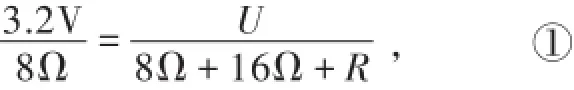
当滑动变阻器R接入电路的电阻减小了8Ω，设此时串联电路电流为I′，同理得

由①÷②得R=16Ω，

把R=16Ω代入①得U=16V.

（3）当S1、S2闭合、S3断开时，R0与滑动变阻器R并联.由根据P=可知当滑动变阻器接入电路的电阻最大时，电路消耗的功率最小.

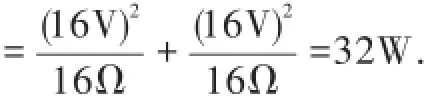
答案：参见解析.

四、让相等量——并联电路中各支路两端电压搭桥

例4（2016·安徽）实际测量中使用的大量程电流表是由小量程电流表改装而成的.图中G是满偏电流（即小量程电流表允许通过的最大电流）Ig=1mA的电流表，其电阻Rg=100Ω.图为某同学改装后的电流表电路图，R1、R2为定值电阻.

若使用a和b两个接线柱时，电表的量程为3mA；若使a和c两个接线柱时电表的量程为10mA.求R1、R2的阻值.

图4

解析：读图可知，若使用a和b两个接线柱时，电阻R1、R2串联后与Rg并联，此时通过b点电流是3mA.设通过电阻R1、R2的电流为I，串联后总电阻为R总，则I=I量程-Ig=3mA-1mA=2mA，故根据并联电路各支路电压相等、欧姆定律可得方程：

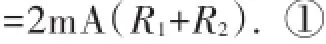
即U=1mA×100Ω若使用a和c两个接线柱时，电阻Rg、R2串联后与R1并联，此时通过c点电流是10mA.设通过电阻R1的电流为I1，Rg、R2串联后总电阻为R总′，则I1=I量程′-Ig=10mA-1mA=9mA，故根据并联电路各支路电压相等、欧姆定律可得方程：

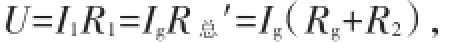
即U=9mA×R1

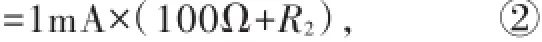
联立①、②得R1=15Ω，R2=35Ω.

答案：R1、R2的阻值分别为15Ω、35Ω.

五、综合运用不同恒量搭桥

例5（2016·绵阳）如图5所示，电源电压保持不变，R2=4Ω，开关S闭合后，电压表读数为7.2V，电流表读数为1.8A；由于某个电阻断路，电压表读数变为16V，电流表读数变为2A.求：

（1）断路前后R3的功率之比；

（2）R1的阻值；

（3）电源电压U和R0的阻值.

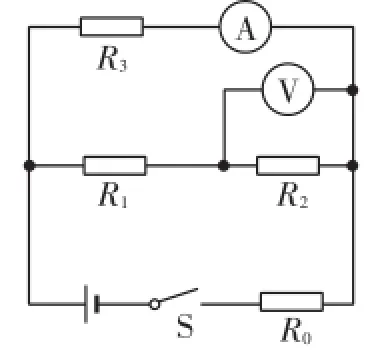
图5

解析：（1）某个电阻断路前后，电流表均测通过R3的电流.设通过R3的电流分别为I3、I3′，消耗功率分别为P3、P3′，则对于定值电阻R3，由P=I2R可得，故有

（2）由题意和电路图可知，当某个电阻断路时，由于电流表、电压表均有示数，所以断路的电阻不可能是R1和R3，只能是R2.此时，R0与R3串联，电压表测R3两端的电压，电流表测电路中的电流，故得R3的阻值：

R2没有断路时，R1与R2串联后与R3并联、再与R0串联，电压表测R2两端的电压，电流表测R3支路的电流.设并联电路中各支路两端的电压均为U′，则根据欧姆定律和串联电路电流、电压关系可得方程组

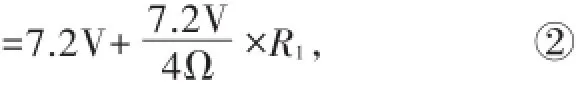
联立①、②得R1=4Ω.

（3）R2没有断路时，干路电流：

即通过R0的电流I0=3.6A.

设电源电压为U，则

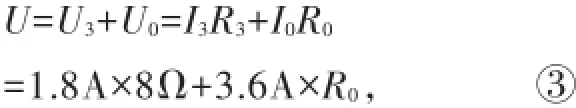
R2断路时，同理可得

联立③、④得R0=1Ω，U=18V.

答案：（1）断路前后R3的功率之比为81∶100；（2）R1的阻值为4Ω；（3）电源电压为18V，R0的阻值为1Ω.