概率的应用易错点剖析

□

概率的应用易错点剖析

□邹兴平

同学们在应用概率解决实际问题过程中，若一时把握不准，就会出现一些错解.下面就一些常见的错解加以剖析，以帮助同学们避免出现同样的错误.

易错点一、抽签结果的可能性判断出错

例1在一个不透明的盒子中装有红、白、蓝三种颜色的竹签，这些竹签只有颜色不同，从中任意抽出一支，抽到三种颜色的可能性相同吗？

错解：从中任意抽出一支签，抽到三种颜色签的可能性相同.

分析：如果三种颜色的竹签的数量都相同，那么从中任意抽出一支签，抽到三种颜色签的可能性相同；如果三种颜色的竹签的数量不相同，那么从中任意抽出一支签，抽到三种颜色签的可能性就不相同，数量多的颜色的竹签抽到的可能性更大.

正解：抽到三种颜色签的可能性不一定相同.

易错点二、掷骰子点数概率判断方法出错

例2抛掷两枚骰子，两个正四面体骰子的各面上分别标明数字1，2，3，4，如同时投掷这两个正四面体骰子，则着地的面所得的点数之和等于5的概率为多少?

错解：因为向上一面点数之和最小为2、最大为8，共有7种不同的结果，所以向上一面的点数之和为5的概率是

分析：可利用树状图分析：

共有16种情况，着地的面所得的点数之和等于5的共有4种，则此种情况的概率为

正解：向上一面的点数之和为5的概率是

易错点三、摸球游戏中概率计算出错

例3在一个不透明的口袋中，装有5个红球3个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（）. A.B.C.D.

错解：P（摸到红球）＝故选A.

分析：摸球时，袋子里是8个球，而不是5个球.概率的计算就是要求用分数来表示事件发生的可能性的大小.从概率的意义来看，要求某一事件发生的概率，必须且只需弄清两个数：操作过程中该事件可能发生的结果数和该事件所有可能发生的各种情况的总数.

正解：P（摸到红球所以应选C.

易错点四、游戏方案的公平性判断出错

例4大双、小双的妈妈申购到一张恩施大峡谷旅游景点的门票，兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球，设计这样一种游戏确定谁去：口袋中放着分别标有数字1、2、3的三个小球，且已搅匀，大双、小双各蒙上眼睛有放回地摸1次，大双摸到偶数就记2分，摸到奇数记0分；小双摸到奇数就记1分，摸到偶数记0分，积分多的就得到门票（若积分相同，则重复第二次）.请问这个游戏方案对双方是否公平？

错解：P（大双摸到偶数）＝小双摸到奇，所以这个游戏方案对双方都公平.

分析：不能从找“摸到偶数”“摸到奇数”角度考虑，因为“摸到偶数”、“摸到奇数”的机会并不均等.可能出现的所有结果列树状图如下（见下页）：

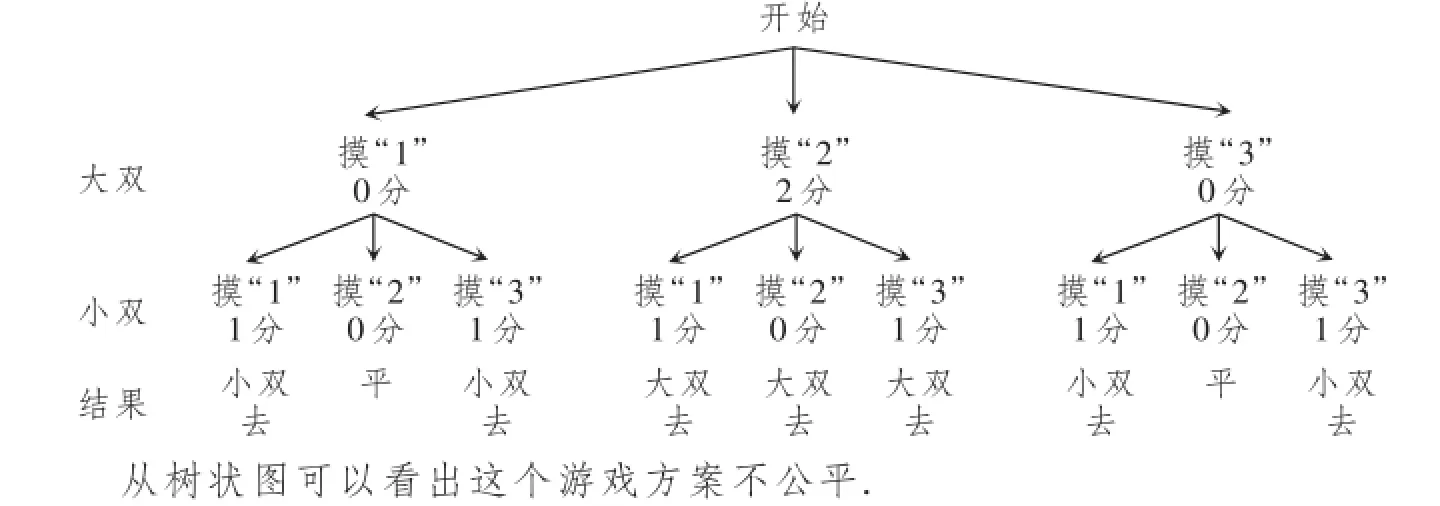
正解：这个游戏方案不公平.P（大双去）＝，这个游戏方案对小双有利.

易错点五、用频率估计概率出错

朝上的点数出现的次数1 7 2 9 3 6 4 8 5 6 2 0 1 0

例5小颖和小红两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了60次实验，实验的结果如上：

（1）计算“3点朝上”的频率和“5点朝上”的频率，

（2）小颖说：“根据实验，一次实验中出现5点朝上的概率最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗？为什么？

错解：（1）“3点朝上”出现的频率是，“5点朝上”出现的频率是

分析：（1）正确.（2）都错误，只有当实验的次数足够大时，该事件发生的频率稳定在事件发生的概率附近；因为事件发生具有随机性，故“6点朝上”的次数不一定是100次.

正解：小颖的说法是错误的.这是因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的频率最大.只有当实验的次数足够大时，该事件发生的频率才会稳定在该事件发生的概率附近.小红的判断是错误的，因为事件发生具有随机性，故“6点朝上”的次数不一定是100次.