基于视线轨迹匹配的遥感相机敏捷成像几何形变分析
武奕楠 张然峰 韩双丽
(中国科学院 长春光学精密机械与物理研究所,长春 130033)
基于视线轨迹匹配的遥感相机敏捷成像几何形变分析
武奕楠 张然峰 韩双丽
(中国科学院 长春光学精密机械与物理研究所,长春 130033)
由于航天遥感相机在敏捷成像过程中姿态和成像方位的变化,以及地球曲率的影响,会导致像面空间几何映射形状发生不同程度的形变。文章分析了遥感相机的敏捷成像模式及特点;根据时间延迟积分(TDICCD)遥感相机的成像特点,建立了基于共线方程的几何配准模型,通过追迹地面点精确地描述任意姿态下的空间成像几何数学关系;通过样例计算各种工况下的整个视场对应的像元地面分辨率,分析了在各种敏捷成像状态下的几何形变情况。以在轨实际图像进行数据比对,结果表明平均误差小于0.009m。该方法同样可应用于其它类型航天遥感相机在不同姿态下的几何形变分析。
敏捷成像 几何形变 共线方程 地面分辨率 航天遥感
0 引言
随着空间光学技术的不断发展,航天遥感相机在大视场、高分辨率等技术指标方面也在不断提高。目前为满足更多的图像应用方向进一步提高相机的地面图像采集效率,通常需要遥感相机采取敏捷成像方式。遥感相机敏捷成像能实现一个轨道周期内,获得不规则曲线分布的目标条带图像,解决了目前传统成像利用多次平行飞行方向推扫成像拼接曲线目标区域的问题[1-2]。敏捷成像往往需要卫星大角度姿态机动,由于姿态和视线方位的变化和本身地球曲率的影响,对地成像会产生复杂的几何变形[3-4],因此需要进行几何校正以实现后续图像产品的拼接。
目前遥感图像几何形变校正主要是通过建立校正变换函数来实现,核心思想是用校正函数来建立影响坐标和地面坐标之间的数学关系。目前采用的数学校正模型主要有多项式法、有理函数模型、共线方程法等[5-8]。多项式法原理直观,计算较为简单。有理函数模型是近年来兴起的一种遥感图像几何校正方法,校正计算独立于像面和地面坐标系统。相比多项式法,是几何模型的一种更普遍和准确的表现形式,校正精度高于多项式法。张过等建立了推扫式光学卫星影像系统几何校准产品的三维几何模型,用有理函数模型表示光学卫星影像系统几何校准产品的高程起伏引起的变形规律,提高了影像定向精度[9]。基于构像模型的共线方程法不需要提供参考图像和采集地面控制点数据,便于采用嵌入式系统自动实现,在遥感图像几何校正中得到广泛的应用。Sebastien Leprince利用投影变换模型及DEM 对SPOT卫星图像进行正射校正[10],胡春晖利用该方法实现了指向镜低频正弦振动下航天遥感器图像的畸变校正[11]。袁修孝等根据遥感卫星传感器对地扫描成像过程中 CCD线阵列侧视角匀速变化的原理,从理论上改进了基于仿射变换的高分辨率卫星遥感影像严格几何处理模型,推导了地物与影像间的正反算公式[12]。
针对航天遥感相机在不同的敏捷状态成像时存在各异的几何形变,本文建立了基于共线方程的成像几何模型,通过推导建立瞬态像点与地面轨迹点的严格数学关系,再通过逐点匹配进一步计算在不同成像姿态下的像元地面分辨率,可更直观地反映各种敏捷成像状态下的图像几何形变情况,最后通过比较实际图像样本进行了验证。
1 敏捷成像模式及特点
1.1 敏捷成像模式

图1 侧摆成像示意图Fig.1 Diagram of scrolling imaging
目前,遥感相机的成像模式主要包括:星下点(平飞)成像模式、侧摆成像模式、俯仰(前后摆)成像模式和俯仰加侧摆成像模式[13]。星下点成像是最传统的成像模式,侧摆角和俯仰角均为0°,仅通过调整偏航角以匹配像移偏流角。该模式下遥感相机沿卫星轨道在地球表面的投影,推扫出与地面投影走向一致的条带。侧摆成像是通过调整卫星横滚角,以实现对卫星轨道在地面投影区域两侧的区域进行推扫,通过进一步规划可以实现多轨连续成像,拼接成一幅具有多个条带宽度的条带。侧摆成像示意图见图1。卫星侧摆角度为φ,某一右侧摆成像条带如地面投影所示。俯仰成像是通过调整卫星俯仰角,以实现对卫星前后方区域的成像,常应用在立体成像领域。侧摆加俯仰成像包括了卫星横滚角和俯仰角的调整,可以最大限度地扩大卫星相机的地面覆盖范围,通常应用在多条带拼接和定点侦查领域。上述几种成像模式中除了星下点成像,都属于敏捷成像模式,可以根据卫星相机的任务需求调整卫星姿态,以实现对目标区域的快速成像。
1.2 几何形变分析
由于地球曲率、成像时大角度姿态机动及卫星姿态稳定度等因素会导致遥感图像存在几何形变,即图像上的等间距像元间所对应的地面距离并不相等,如图2所示。遥感图像几何校正的目的就是为了消除原始图像中的几何形变,通过像元几何位置变换和像元灰度重采样得到校正后的数字影像[14-15]。
由于几何形变会导致像面上不同位置的CCD像元对应的地面分辨率分布不均,所以确定像面上各像点与地面图像的准确映射关系,通过求取像元地面分辨率来反映在不同成像模式下的几何形变分布。采用共线方程模型对遥感成像空间几何形态进行描述[16-18],需要建立在空间各坐标系严格变换的基础上,同时根据传感器的构像方式建立合适准确的几何模型。
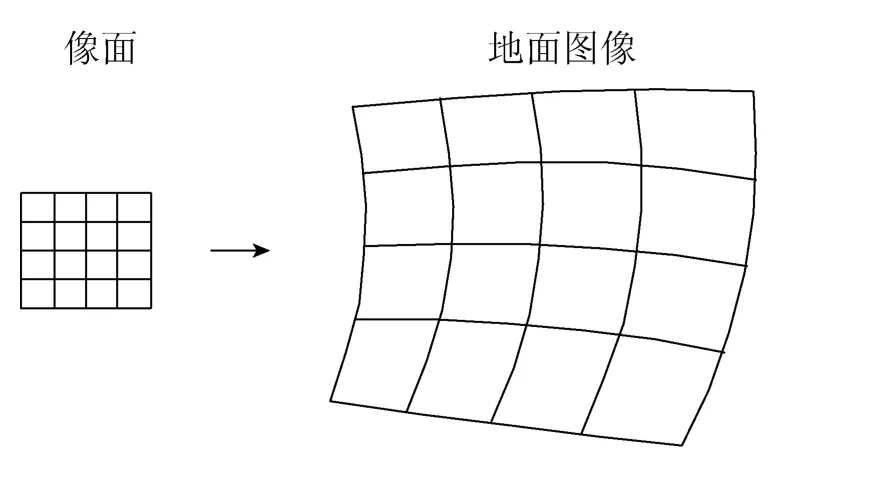
图2 几何形变示意图Fig.2 Diagram of geometric distortion
2 基于视线轨迹匹配的几何配准模型
2.1 坐标系定义
地心惯性坐标系 I(i1,i2,i3):原点 I0在地心,i2轴指向北极,i3轴为卫星的轨道平面和赤道面的交点,i1轴垂直于i2和i3两轴形成的平面,该坐标系保持惯性空间。
卫星轨道坐标系 B(b1,b2,b3):原点 B0在轨道上,b1轴指向轨道前向,b3轴指向天顶,b1和 b3在轨道面内,b2轴与轨道面垂直。B系在I系里,沿轨道以角速度Ω作轨道运动。
卫星本体坐标系S(s1,s2,s3):该坐标系原点与B系原点重合,卫星无姿态运动时S系和B系重合,卫星的三轴姿态0φ,θ0,Ψ0即为S系在B系内的横滚角、俯仰角、偏航角。
相机坐标系 C(c1,c2,c3):相机物镜的光学中心为该坐标系的原点,当相机在卫星内无安装误差时,相机坐标系与卫星本体坐标系重合。
2.2 构像方程建立
设摄像中心点S与地面点A在地面摄影测量坐标系D-XYZ中的坐标分别为Xs、Ys、Zs和Xa、Ya、Za,相应的像点p在像空间辅助坐标系下的坐标为X、Y、Z。由于摄像中心、地面点和像点三点共线,因此由相似三角形关系可以得到[19]

式中 λ为比例因子。
对于线阵TDICCD相机,图像上每一行都有独立的外方位元素,设卫星飞行方向为y,x在像面上垂直于y方向,每一像点在像面上的坐标均为y=0,易得共线方程为

式中 f为相机焦距;a1、a2、a3、b1、b2、b3、c1、c2、c3由该成像时刻的外方位角元素φ θ Ψ,, (分别为横滚角、俯仰角、偏航角)确定[20]。得到逆算式

2.3地心惯性坐标系下求解地面点
以地心惯性坐标系作为空间固定惯性参考系,由于相机物镜的光学中心为相机坐标系的原点,当相机坐标系与卫星坐标系重合时,可得摄像中心点在惯性参考系下的坐标为

式中 L为卫星轨道地心距;i0为卫星轨道倾角;ρ为成像时刻卫星轨道幅角。

式中 δ为成像时刻卫星星下点纬度。
地球椭球方程为

式中 ae,be分别是地球的长短半轴。
联立式(3)、(4)、(7),确定像面上像点p的像面坐标,即可计算像点对应的地面点A的坐标。
2.4 逐点匹配计算像元分辨率
通过构像方程和坐标变换可以求解像面上任意点位置对应的地面坐标位置。选取像面上像点的左右边界坐标,求解出所对应的两个地面位置坐标,即可求解出该像点所对应的地面像元分辨率。设像点的左右边界坐标分别为 x1、x2,成像时刻姿态角为φ,θ,Ψ,星下点纬度为 δ,卫星轨道和相机参数已确定。Xa,1,Ya,1,Za,1和Xa,2,Ya,2,Za,2分别为待求的地面位置坐标,地面像元分辨率Mp,计算公式如下
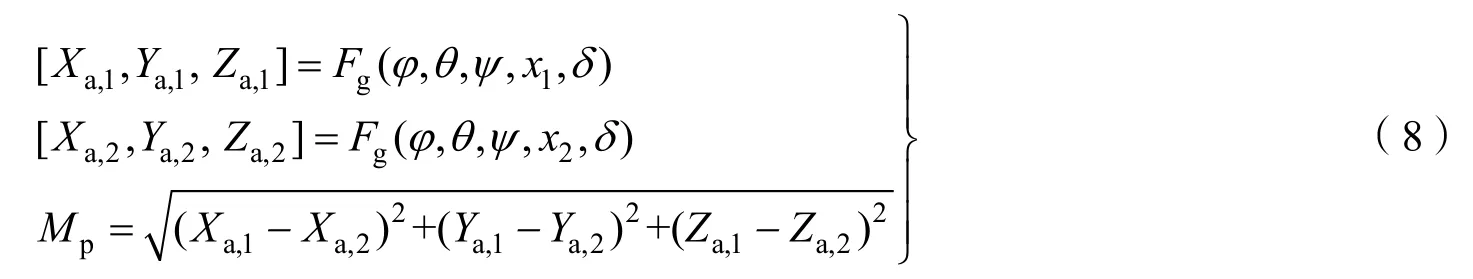
式中 Fg代表式(3)、(4)、(7)构成的联立方程组。
3 验证与分析
3.1 样例计算与分析
通过样例计算地面像元分辨率,分析卫星相机在不同工作状况下的成像几何形变情况。某卫星相机轨道高度为490km,轨道倾角为102°,相机焦距为1.25m。焦平面由19片TDI探测器拼接,每片包括8 192个像元,像元尺寸为3.5μm。
以焦平面上各像元作为待计算特征点,计算卫星相机在平飞状态下,在不同星下点纬度成像所对应的地面分辨率,如图3(a)所示。图中横坐标为像面上的像元数编号,其中第1个像元为像面右端点。纬度区域为北纬 60°至赤道。在平飞状态下,相机焦平面上各位置像元所对应的视线长度差距较小,但由于地球曲率的影响,视场两端对应的地面分辨率更大;由于轨道倾角的影响,左右视场两端地面分辨率也并非完全对称分布。由于地球为椭球体,纬度越高、地球半径越小,视线长度越长、地面分辨率越大。
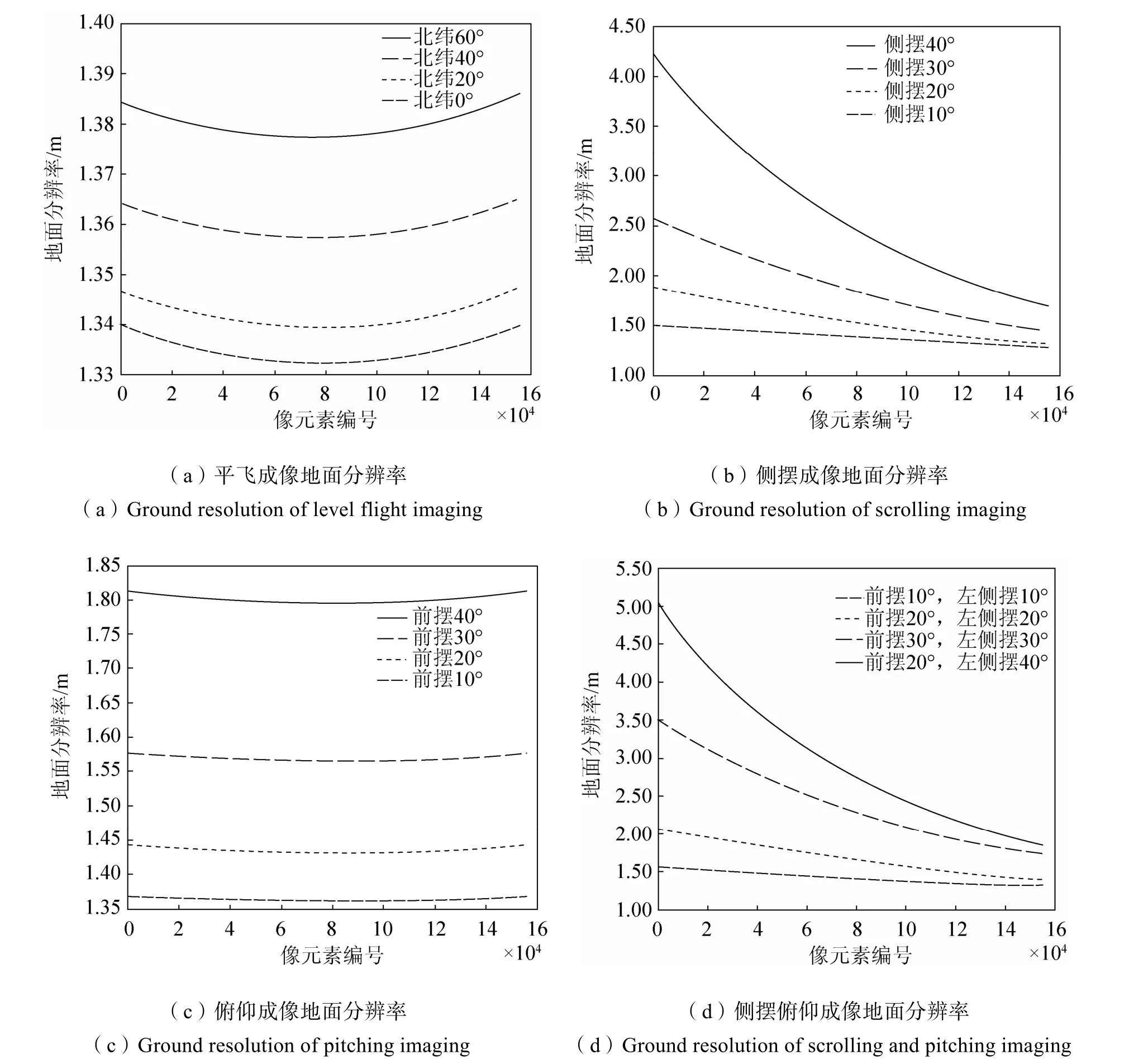
图3 像元地面分辨率分布Fig.3 Distribution of pixel ground resolution
同理,以10°为间隔,星下点纬度为北纬20°时,计算卫星相机左侧摆10°至40°工况下地面分辨率,如图3(b)所示。显然由于姿态角度的增大,成像几何形变越大,像面上各像元地面分辨率的相对差异越大。在侧摆40°工况下,视场两端地面像元分辨率差异最大,分别为4.23m和1.68m。以10°为间隔,星下点纬度为北纬20°时,计算卫星相机前摆10°至40°工况下地面分辨率,如图3(c)所示。随着前视角的增加,视线长度会变长,地面分辨率会增大,对比侧摆成像,同一角度下各位置像元的地面分辨率相对差异较小,前摆 40°时最大和最小像元分辨率数值相对差值不超过 1.07%,平飞成像相对差值为0.67%,几何形变程度和平飞时基本相当。
为满足大范围灵活成像的要求,卫星相机往往需要横滚方向和俯仰方向同时做机动。计算卫星相机在多组姿态角度下的地面分辨率,如图 3(d)所示。显然,随着视角的增大地面分辨率绝对值和相对差值都增大;相比于俯仰角,侧摆角对整个像面所对应的地面形变影响更大。
3.2 地面靶标测试
相比于半实物仿真实验,以在轨卫星对地所成图像验证算法更为准确。选取某卫星相机对云南地区靶场在不同时刻和姿态角度下所成的图像,由于地面靶标精确尺寸已知,通过图像易求得所对应的地面分辨率。图4为2012年6月对该靶场的平飞成像。

图4 地面靶标成像样本Fig 4 Sample image of ground target
根据实际图像样本的成像状态,通过理论模型计算地面分辨率,并和实际图像数据作比对。采用的图像样本和计算结果如表1所示。计算地面分辨率理论值和实际值之间的误差,平均误差小于0.009m。在成像机动角度比较大的情况下,误差较大,主要是由于卫星在大角度机动时,姿态稳定度较差,而平飞时由于姿态稳定状态最好,误差很小。其他误差源还包括大气折射、卫星系统误差等。

表1 地面分辨率数据比对Tab.1 Contrast of ground resolution
4 结束语
针对航天遥感相机在敏捷状态成像时像面空间几何映射形状产生不同程度的形变,本文根据线阵遥感相机的成像特点,建立了基于严格共线方程的几何配准模型,通过逐点匹配可以计算任意视场位置的像元地面分辨率,可以更直观、量化的体现几何形变情况。通过样例分析,相比于平飞成像和俯仰成像,侧摆成像时像面上各点地面分辨率差值更大,整个像面所对应的形变越大。以在轨相机对地面靶标实际成像作为对比,计算地面分辨率平均误差小于0.009m,验证了几何模型的正确性。该方法可应用于遥感相机在不同星下点纬度和飞行姿态下的在轨所成图像的预测和复算。
References)
[1]李宪圣, 任建岳, 任建伟, 等. 空间相机在轨成像模式的建立[J]. 光学精密工程, 2015, 23(7): 1852-1858.
LI Xiansheng, REN Jianyue, REN Jianwei, et al. Establishment of Image Model for on-board Space Camera[J]. Opt. Precision Eng, 2015, 23(7): 1852-1858.(in Chinese)
[2]武星星, 刘金国. 基于地球椭球的空间相机侧摆摄影像移补偿[J]. 光学精密工程, 2014, 22(2): 352-359.
WU Xingxing, LIU Jinguo. Image Motion Compensation of Scroll Imaging for Space Camera Based on Earth Ellipsoid[J]. Opt. Precision Eng, 2014, 22(2): 352-359. (in Chinese)
[3]岳春宇, 何红艳, 鲍云飞, 等. 多视场遥感图像虚拟焦面拼接理论误差分析[J]. 航天返回与遥感, 2015, 36(2): 60-68.
YUE Chunyu, HE Hongyan, BAO Yunfei, et al. Error Analysis of Remote Sensing Image Mosaic Based on Virtual Focal Plane[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(2): 60-68. (in Chinese)
[4]王力, 贾平, 张叶, 等. 复杂地物条件下基于线特征的异源景象匹配[J]. 中国光学, 2016, 9(1): 81-88.
WANG Li, JIA Ping, ZHANG Ye, et al. Multi-sensor Image Matching Based on Line Features Under Complex Object Conditions[J]. Chinese Optics, 2016, 9(1): 81-88. (in Chinese)
[5]王静, 周峰, 潘瑜, 等. 超模式斜采样遥感图像超分辨复原方法[J]. 航天返回与遥感, 2012, 33(1): 60-66.
WANG Jing, ZHOU Feng, PAN Yu, et al. Super-resolution Restoration of Super-tilting Mode Remote Sensing Image[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(1): 60-66. (in Chinese)
[6]付天骄, 张立国, 王文华, 等. 空间相机图像复原的实时处理[J]. 光学精密工程, 2015, 23(4): 1122-1130.
FU Tianjiao, ZHANG Liguo, WANG Wenhua, et al. Real-time Processing of Image Restroration for Space Camera [J]. Opt. Precision Eng, 2015, 23(4): 1122-1130.(in Chinese)
[7]CHEN J, TIAN J. Real-time Multi-modal Rigid Registration Based on a Novel Symmetric-SIFT Descriptor[J]. Progress in Natural Science, 2009, 19(5): 643-651.
[8]常琳, 金光, 杨秀彬. 航天TDICCD相机成像拼接快速配准算法设计与分析[J]. 光学学报, 2014, 34(5): 0511001.
CHANG Lin, JIN Guang, YANG Xiubin. Fast Registration Algorithm Design and Analysis of TDICCD Camera Assembly imaging[J]. Acta Optica Sinica, 2014, 34(5): 0511001. (in Chinese)
[9]张过, 厉芳婷, 江万寿. 推扫式光学卫星影响系统几何校正产品的3维几何模型及定向算法研究[J]. 测绘学报, 2010, 39(1): 34-38.
ZHANG Guo, LI Fangting, JIANG Wanshou. Study of Three-dimensional Geometric Model and Orientation Algorithms for Systemic Geometric Correction of Push-broom Optical Satellite Image[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 34-38. (in Chinese)
[10]SÉBASTIEN L, SYLVAIN B, FRANÇOIS A. Automatic and Precise Orthorectification, Coregistration, and Subpixel Correlation of Satellite Images, Application to Ground Deformation Measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(6): 1529-1532.
[11]胡春晖, 颜昌翔, 邵建兵. 指向镜低频正弦振动下遥感器图像的畸变及校正[J]. 光学学报, 2013, 33(4): 0428002.
HU Chunhui, YAN Changxiang, SHAO Jianbing. Pointing Mirror Low Frequency Sine Oscillation Induced Remote Sensor Image Distortion and Correction[J]. Acta Optica Sinica, 2013, 33(4): 0428002. (in Chinese)
[12]袁修孝, 曹金山, 姚娜. 顾及扫描侧视角变化的高分辨率卫星遥感影像严格几何模型[J]. 测绘学报, 2009, 38(2): 120-124.
YUAN Xiuxiao, CAO Jinshan, YAO Na. A Rigorous Geometric Model Considering the Variety of Side Watch Angle for High-resolution Satellite Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(2): 20-124. (in Chinese)
[13]巩盾. 空间遥感测绘光学系统研究综述[J]. 中国光学, 2015, 8(5): 714-724.
GONG Dun. Review on Mapping Space Remote Sensor Optical System[J]. Chinese Optics, 2015, 8(5): 714-724. (in Chinese)
[14]周前飞, 刘晶红, 王宣, 等. 航空变焦距斜视成像几何畸变的自动校正[J]. 光学精密工程, 2015, 23(10): 2927-2942.
ZHOU Qianfei, LIU Jinghong, WANG Xuan, et al. Automatic Correction of Geometric Distortion in Aerial Zoom Squint Imaging[J]. Opt. Precision Eng, 2015, 23(10): 2927-2942. (in Chinese)
[15]李瀛搏, 胡斌, 胡海彦, 等. 双基高比线面阵结合立体测绘几何模型的构建[J]. 航天返回与遥感, 2015, 36(1): 32-42.
LI Yingbo, HU Bin, HU Haiyan, et al. Building of Geometric Processing Model Based on Double Baseline with Combination of Linear and Area Array Sensor Stereo Photogrammetric Mode[J]. Spacecraft Recovery & Remote Sensing,2015, 36(1): 32-42. (in Chinese)
[16]王卫兵, 王挺峰, 郭劲. 基于星载光电成像跟踪测距的空间目标定轨[J]. 光学精密工程, 2015, 23(2): 528-539. WANG Weibing, WANG Tingfeng, GUO Jin. Orbit Determination for Space Target Based on Opto-electrical Imaging, Tracking and Ranging on Satellite[J]. Opt. Precision Eng, 2015, 23(2): 528-539.(in Chinese)
[17]苗壮, 何斌, 王俊琦, 等. 空间相机摆扫成像建模及摆镜角速度残差分析[J]. 航天返回与遥感, 2015, 36(6): 39-47. MIAO Zhuang, HE Bin, WANG Junqi, et al. Modeling of Space Camera for Whiskbroom Imaging and Analysis of Pendulum Mirror Angular Velocity Residual[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(6): 39-47. (in Chinese)
[18]孙辉, 李志强, 张建华, 等. 机载光电平台目标交会定位[J]. 中国光学, 2015, 8(6): 988-996. SUN Hui, LI Zhiqiang, ZHANG Jianhua, et al. Target Localization with Intersection Measurement for Airborne Electro-optical Platform[J]. Chinese Optics, 2015, 8(6): 988-996. (in Chinese)
[19]杨飞, 金光, 谢金华, 等. 基于在轨成像物理机理的立体测绘相机建模与仿真[J]. 中国光学, 2015, 8(6): 971-979. YANG Fei, JIN Guang, XIE Jinhua, et al. Stereo Mapping Camera Modeling and Simulation Based on the Physical Mechanism of On-orbit Imaging[J]. Chinese Optics, 2015, 8(6): 971-979. (in Chinese)
[20]孙阳, 薛栋林, 郑立功, 等. 基于速度矢量模型的圆轨道空间相机偏流角实时补偿[J]. 红外与激光工程, 2014, 43(7): 2185-2191. SUN Yang, XUE Donglin, ZHENG Ligong, et al. Real-time Drift Angle Compensation Based on Speed Vector Model for Space Camera on Circular Orbit[J]. Infrared and Laser Engineering, 2014, 43(7): 2185-2191.(in Chinese)
Geometric Distortion Analysis of Remote Sensing Camera Agile Imaging Based on Ray Trail Registration
WU Yinan ZHANG Ranfeng HAN Shuangli
(Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China)
The attitude variation and image orientation change of aerospace remote sensing camera in agile imaging mode and the curvature of the earth cause the mapping shape of space geometry on focal plane to be distorted in different degree. Firstly, the mode and characteristics of agile imaging are analysed. Then, according to the imaging characteristics of TDICCD remote sensing camera, a geometric registration model based on collinearity equation is established. The space imaging geometrical mathematics in any attitude is described accurately through tracking ground points. The ground resolution corresponding to pixels of the whole field of view is calculated in various kinds of working situations. The geometric distortion is analysed in differents status of agile imaging. Finally, the result shows everage error is less than 0.009m in comparison with actual image. The method can also be applied to geometric distortion analysis for any other kinds of aerospace remote sensing camera in different attitudes.
agile imaging; geometric distortion; collinearity equation; ground resolution: aerospace remote sensing
V474.2
: A
: 1009-8518(2016)02-0108-08
10.3969/j.issn.1009-8518.2016.02.014
武奕楠,男,1984年生,2010年获北京航空航天大学摄影测量与遥感专业硕士学位,助理研究员。主要从事光电成像技术方面的研究。E-mail:wyn_buaa@163.com。
(编辑:王丽霞)
2016-02-22
国家863计划资助项目(No.863-2-5-1-13B)

