B样条函数在大坝变形数据分析中的应用

王江荣，袁维红，赵 睿，任泰明

(兰州石化职业技术学院，甘肃兰州730060)

B样条函数在大坝变形数据分析中的应用

王江荣，袁维红，赵 睿，任泰明

(兰州石化职业技术学院，甘肃兰州730060)

用参数回归模型分析处理大坝变形数据时存在着变量之间的函数关系需要预先设定的问题，而对于一些波动性大、规律性和整体性较差的大坝变形数据，预选设定函数关系是困难的。为能较好地解决这类问题，建立了一种基于三次B样条函数的非参数回归模型。该模型是一种完全受观测数据驱动的数学模型，具有建模简单、适用强、精确度高和易于程序实现的特点。对出现的模型的系数采用遗传算法求解。实例分析表明，基于三次B样条函数的非参数模型具有较高的拟合预测精度，能够较好地解决实际问题。

变形数据；非参数模型 ；B样条函数；遗传算法；插值预测

0 引 言

大坝变形数据处理模型大多采用了参数回归模型[1-4]，这类回归模型存在着变量之间(变形值—时间)的函数关系需要预先设定的问题，如果设定的函数关系与实际情况吻合，则统计推断精度会比较高；反之，模型的统计推断就会出现较大偏差，拟合预测效果会非常差，甚至没有什么实际意义。但在实际问题中，变形实测数据之间的变量关系往往难以确定，因此利用参数回归模型处理这类数据难以取得理想效果。而非参数回归模型是一种不依赖于总体样本分布，仅受数据驱动以及不受变量分布约束的模型，和参数模型相比，这类模型是更符合实际问题的一种回归模型。选择什么样的非参数模型是解决问题的关键。样条函数，尤其是三次B样条函数是一种非参数模型，具有良好的分段光滑性和全局逼近能力[5]。因此，本研究拟采用三次B样条函数拟合变形数据，并采用外插值延拓方法对建模以外的变形数据进行预测。由于三次B样条函数拟合存在着矩阵求逆的问题，当观测数据越多时，矩阵的阶就越高，求逆就越繁琐。为了解决这个问题，本文采用遗传算法( Genetic algorithms，GA )求解三次B样条函数的拟合系数。

1 基于三次B样条函数的非参数回归模型

基于B样条函数的非参数回归模型是由B样条基函数[6]通过线性组合而构成的，它可以任意逼近连续函数[7]。为便于研究，本文采用均匀(任意相邻节点间距离相等)三次B样条基函数构建非参数回归模型。

1.1 均匀三次B样条基函数

均匀三次B样条基函数参考文献[8]。即

(1)

式中，ti(i=0,1,2,…,n-1)为节点(它是时间t所属区间的n等分点)，常量h=ti+1-ti(i=0,1,2,…,n-1)。

由式(1)可知，Bi,3(t)的形状仅与ti及h的选择有关(形状由节点和步长唯一确定)，而其他的B样条Bj,3(t)可由Bi,3(t)平移变换得到，即Bj,3(t)=Bi,3(t-(j-i)h)。

1.2 三次B样条回归模型

由式(1)可知，欲确定第i个三次(即4阶)B样条Bi,3(t)，需要用ti,ti+1,ti+2,ti+3,ti+4共5个节点，称区间[ti,ti+4]为Bi,3(t)的支撑区间。t0t1t2…tn+4为三次B样条函数的节点序列(即数据拟合中共需n+1个三次B样条基函数Bi,3(t))。用三次B样条函数可以将非参数模型m(t)(m(t)是未知回归函数)近似地表示为

(2)

式中，xi为观测时间点；模型系数，Φ={θj|j=0,1,2,…,n}，采用遗传算法求解。

2 工程实例

某大坝变形监测数据[9]见表1。在前32期数据中等间隔地取期数为3、7、11、15、19、23、27对应的7个数据为测试数据，其余25个数据为建模数据，后4期即33、34、35、36对应的数据用于外插预测检验数据。

前32期的观测数据点如图1所示。从图1可以看出，数据点波动性较大，规律性和整体较差，故难以用参数模型(需事先选定)来拟合此类数据点，而选用基于B样条函数的非参数模型能够较好地解决此类问题。

表1 大坝变形监测数据

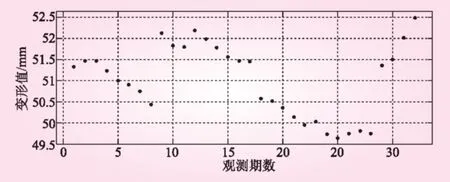
图1 原始大坝切向位移监测数据

3 三次B样条拟合系数估算

按表1中1～32期观测数据点设定均匀控制节点L=[0，4，8，12，16，20，24，28，32，36，40]。按式(1)每5个节点确定一个三次B样条基函数，共确定7个三次B样条基函数，分别记作B0,3(t),B1,3(t)，…，B6,3(t)(具体表达式及图形在此略去)，由此构建的非参数回归模型为

(3)

下面采用遗传算法估算模型系数Φ=[m0,θ0,θ1,θ2,…,θ6]。定义目标函数

(4)

在MATLAB工作窗口利用gatool命令打开遗传算法的GUI，在Fitnessfunction窗口输入@finess，在Numberofvariables窗口输入待估参数个数8，在边界约束Lower输入-80*ones(1，8)，在Upper输入 80*ones(1，8)，种群规模为50，迭代次设为1 000，其他参数选用缺省值，然后单击Start按钮执行遗传算法。迭代400次后输出的最优模型系数为：m0=51.387 9，θ0=-0.904 2，θ1=1.426 6，θ2=-0.145 9，θ3=-1.077 9，θ4=-1.698 4，θ5=-1.893 3，θ6=2.196 7。将这些估算值代入模型(3)，得

(5)

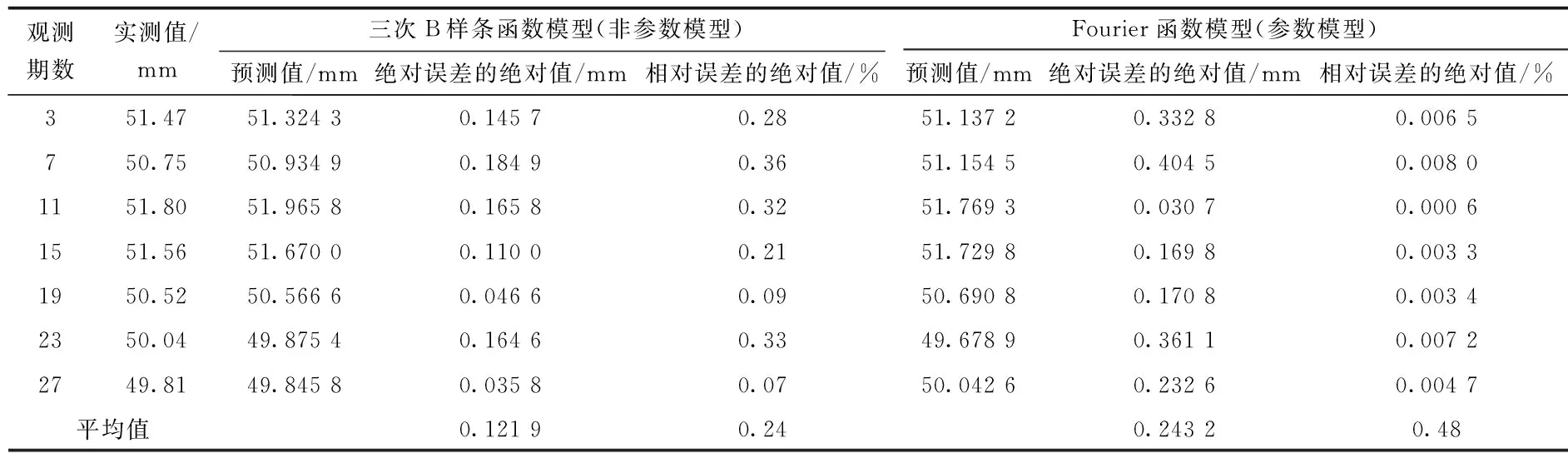
表2 模型预测值比较

表3 均匀三次B样条函数外插预测值

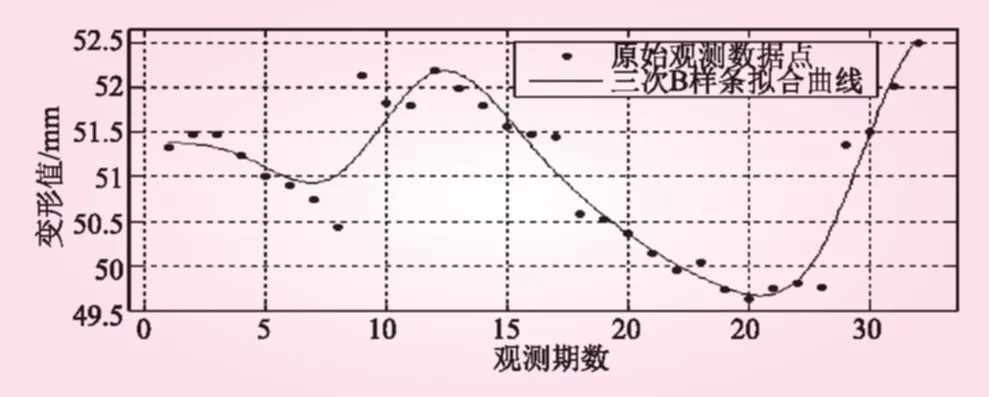
图2 均匀三次B样条函数的拟合预测曲线

作为对比，采用傅里叶函数建模(参数模型)如下

y=51.93+1.18cos(0.133 5t)-1.21sin(0.133 5t)-
1.123cos(0.133 5t)-0.871 9sin(0.133 5t)

(6)

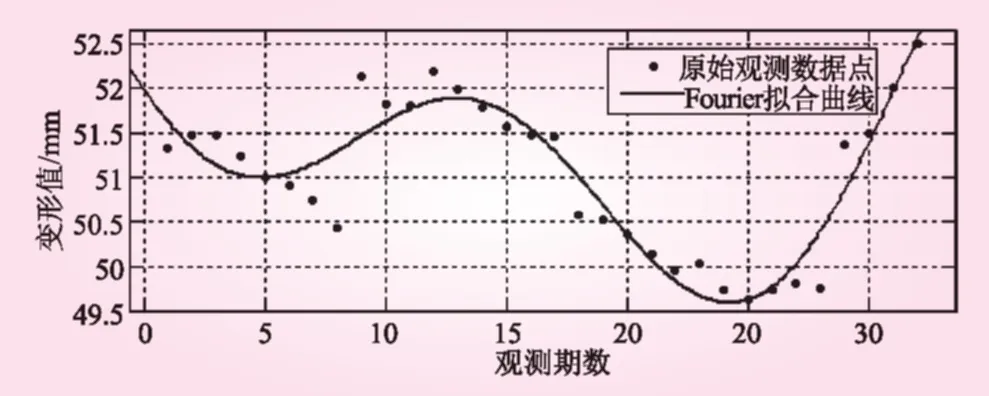
图3 傅里叶函数拟合效果

从表2可以看出，基于三次B样条的非参数模型具有较高的预测精度(最大绝对误差不超过0.1849，相对误差最大不超过0.33%)，预测效果好于Fourier函数模型，预测精度提高近一倍，预测结果值得信赖。由于三次B样条曲线是连续变化的，所以可通过该模型得到观测时间段内任意时间点的大坝变形值，这对研究大坝变形规律是非常有益的。利用前32期的拟合预测值对表1中后4期的变形值进行预测，计算过程采用MATLAB一维外插运算函数[10]，即Y=interp1()，预测结果见表3。

从表3可看出，三次B样条函数模型的预测精度高于傅里叶函数模型，最大绝对误差不超过0.379 2，相对误差最大不超过0.43%，能够满足工程需要。但是，需要指出的是，不管用哪种插值方法，当插值点位于已知数据集合外时，插值运算对该处函数值的估计都很可能与实际函数值相比会有较大的偏差，从这点上讲，本文得出的预测结果是令人满意的。

4 结 论

(1)当变形数据呈现出波动性大、整体性差且无规律状态时，就难以选择合适的参数模型作数据拟合预测，选择不当时就会出现较大误差。而非参数模型是一种仅受数据驱动的模型，更适合实际问题的解决。B样条函数能够任意逼近连续函数(大坝变形是连续变化的)，利用B样条函数构建的非参数模型具有较高的精确度，适合波动大、无规律数据建模。

(2)基于B样条函数的非参数模型非常适合内插值预测，这对研究时间区间内的大坝变形规律具有重要的意义。其缺点是其外插预测能力较差，这是今后需要改进的地方。另外，B样条函数拟合存在着矩阵求逆的问题，观测数据越多，矩阵的阶就越高，求逆就越繁琐。为了解决这个问题，可采用遗传算法求解B样条拟合系数。

(3) B样条基函数形状仅与讨论域(区间)上的节点(控制节点)有关，这些基函数的线性组合构成了的非参数回归模型，该模型具有良好性的适用性、通用性，且容易通过程序实现，为解决大坝变形问题提供了一种新思路、新方法。

[1]王江荣. 高斯函数模型在变形监测数据处理中的应用[J]. 金属矿山，2015(4)：178-181.

[2]王江荣. Richards生长曲线模型在大坝变形监测数据处理中的应用[J]. 矿山测量，2015(5)：59-61.

[3]王鸣，易武，邓永煌. 基于自适应搜索权重的滑坡位移组合预测[J]. 水力发电，2016，42(2)：26-28，37.

[4]魏迎奇，孙玉莲. 大坝沉降变形的灰色预测分析研究[J]. 中国水利水电科学研究院学报，2010，8(1)：25-29.

[5]冯玉瑜，曾芳玲，邓建松. 样条函数与逼近论[M]. 合肥：中国科学技术大学出版社，2013.

[6]温伟斌. 基于B样条插值的数值流形方法与时间积分方法的研究[D]. 重庆：重庆大学，2014.

[7]解其昌. 分位数回归方法及其在金融市场风险价值预测中的应用[M]. 北京：中国农业科学技术出版社，2014.

[8]刘昕明. 两类非参数分位数回归模型的研究[D]. 北京：北京化工大学，2013.

[9]张安兵. 动态变形监测数据混沌特性分析及预测模型研究[D]. 北京：中国矿业大学，2009.

[10]王正林，龚纯，何倩. 精通MATLAB科学计算[M]. 北京：电子工业出版社，2012.

(责任编辑 焦雪梅)

Application of B-Spline Function in Dam Deformation Data Analysis

WANG Jiangrong, YUAN Weihong, ZHAO Rui, REN Taiming

(Lanzhou Petrochemical College of Vocational Technology, Lanzhou 730060, Gansu, China)

There is a problem that the functional relationship between variables is necessary to be pre-set when processing dam deformation data by using parameter regression analysis. For the dam deformation data with large fluctuation, poor regularity and poor integrity, the pre-set of function relationship is difficult. In order to better solve this kind of problem, a nonparametric regression model based on Cubic B-spline function is established. The model is a mathematical model of complete observation data driven with the features of simple modeling, strong application, high accuracy and easy programming. The coefficient of model is solved by genetic algorithm. The empirical analysis shows that the new model has high prediction accuracy and can better solve practical problem.

deformation data; nonparametric model; B-Spline function; genetic algorithm; interpolation prediction

2016-03-17

兰州市科学技术局计划项目(兰财建发[2015]85号)；兰州石化职业技术学院科技资助项目(院发〔2015〕69号)；甘肃省科技厅计划项目(1204GKCA004)；甘肃省财政厅专项资金立项资助(甘财教[2013]116号)

王江荣(1966—)，男，甘肃静宁人，教授，硕士，主要从事数据挖掘、数值分析、控制理论与应用方面的研究.

TV698.1

A

0559-9342(2016)12-0115-04