一种基于改进BP神经网络的重载列车驾驶曲线算法研究

谭力天，黄友能，李玲玉

（北京交通大学 电子信息工程学院，北京 100044）

一种基于改进BP神经网络的重载列车驾驶曲线算法研究

谭力天，黄友能，李玲玉

（北京交通大学 电子信息工程学院，北京 100044）

BP神经网络被用于重载列车驾驶曲线研究，利用列车实际驾驶数据进行神经网络学习，描述列车制动时的非线性特性，对列车制动运行过程建模，获得列车制动减压目标值及缓解时间进行运动方程运算，最终获得重载列车驾驶曲线。通过在朔黄线线路上由该模型仿真得到的驾驶曲线和实际列车驾驶曲线比较，结果表明该方法研究驾驶曲线是有效的。

重载列车；神经网络；仿真建模

由于重载列车牵引质量大、编组长且在连续长大下坡道以空气制动为主循环制动，列车管减压呈非线性特性，使自动驾驶很难应用在重载列车，大多采用人工驾驶，因此，对重载列车驾驶曲线的研究十分必要。

国内外众多学者对轨道交通系统列车驾驶运行进行了研究。城轨自动驾驶方面，用模型选择和参数辨识优化，研究列车自动驾驶模型[1～2]。采用自适应模糊控制技术，实现城市轨道交通列车自动驾驶速度控制[3～4]。重载铁路方面，采用分散控制模型对列车单个车辆速度进行控制[5]。采用模型预测控制，分析研究重载列车整体运行过程[6～7]。虽然从模型角度对单个车辆或整个列车进行速度控制，但没有给出具体操控参数。

1 神经网络建模及驾驶曲线研究

本文利用神经网络非线性神经元相互连接进行信息处理和传递的特点研究列车运行过程[6]。根据列车位置与速度等信息，综合列车运行前方线路坡道长度、坡度与限速等参数，建立适当的模型研究列车运行。

1.1 列车运行方程

列车不进行空气制动作用时，列车管保持一定的压强（500/600 kpa），当空气制动时列车管向外放风降低压强使得列车减速，结束后向列车管充风恢复定压保障下次制动能力，这个过程需要足够的时间，操作不当可能造成失控。连续长大下坡道处是司机操控的困难区段，研究列车在以下情形的运行。列车运行前方存在两个或两个以上的连续下坡道，前方下坡道长度不小于2 km。

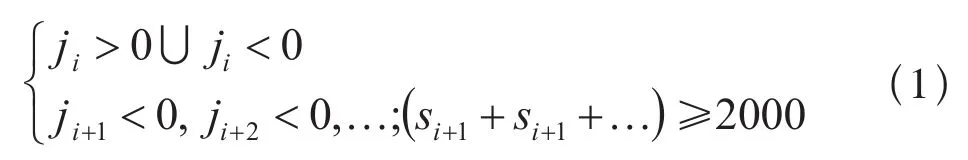
式（1）中，j（‰）表示坡道的坡度，s（m）表示坡道长度，下标表示线路上各坡道。

列车在运行时受到牵引力、制动力及阻力3 种力的作用，并且列车在运行过程中作平移运动的同时还存在回转运动，列车运行时分、距离方程分别为：

式（2）中，c 为列车所受的单位合力，S、v 和t分别为列车运行的距离、速度和时间，ζ 为加速度系数，表示为其中，M 为整个列车的质量，I 为列车作回转运动部分的转动惯量，Rh为回转部分的回转半径，称为回转质量系数，通常取值为0.06。

1.2 BP神经网络建模

神经网络由单个的神经元和其相互之间的加权连接构成，每个神经元都是基本运算的信息处理单元，一般包括输入层、隐含层、输出层，各层都有输出向量、误差向量和权值矩阵。误差反向传播（BP，Back Propagation）神经网络广泛应用于函数逼近、模式识别与分类等，是非线性前馈式网络，可以逼近任意的非线性映射关系，通过改进算法可以获得收敛的快速性，适用于复杂而不易建立精确模型的系统，所以本文采用改进的BP 网络。

模型具有3 层结构，输入层、隐含层和输出层。隐含层传递函数f1为tan-sigmoid 函数，输出层传递函数f2采用线性函数。神经网络各层的输出可以表示为：

上式中，上下标表示神经网络对应的各层，W为权值矩阵，f1和f2为各层的传递函数。输出层神经元输出可以表示为：

式（5）中，xi是神经元输入，分别是输入层和隐含层间的权值和偏差，分别是隐含层和输出层间的权值和偏差。

BP 神经网络有多种训练函数，如梯度下降算法[7]，共轭梯度算法[8]，Levenberg-Marquardt 算法[9]，Broyden-Fletcher-Goldfarb-Shanno（BFGS）拟牛顿算法[10]等。本文在神经网络模型中采用L-BFGS 拟牛顿算法，是BFGS 算法的一种改进算法，不需要计算Hessian 矩阵，这种算法对权值（xk）的更新可以表示为：

gk是xk处的梯度，tk是步长因子，Hk是替换牛顿法中Hessian 逆矩阵的一个易于计算的正定矩阵，区别是它通过保存最近m 次曲率信息来更新权值，m 根据实际情况确定。

神经网络应具有相同量级的输入和输出，如果量级不同对神经网络可能有很大的影响[11]，对数据进行归一化处理，使得所有参数的值域范围限制在[0，1]之间。隐含层节点数过多训练时间增加并且可能出现过拟合，节点数较少训练时间和精度都会被影响。为避免过拟合，对于训练集大小N 应满足条件：

其中，σ 表示网络中的自由参数的总量，ε 表示测试数据中容许分类误差的部分，O(·) 表示所包含的量的阶数。隐含层节点数可以参考以下经验公式：

式（8）中，a 为0 ～ 10 之间的常数，u 为输入层的节点数，z 为输出层的节点数，隐含层节点数n采用试凑法来确定。本文神经网络模型有7 个输入节点，2 个输出节点，通过试凑得到隐含层节点数为11，所以本文神经网络结构为（7×11×2）。

神经网络训练的标准决定训练是否达到精度要求，定义此误差函数为：

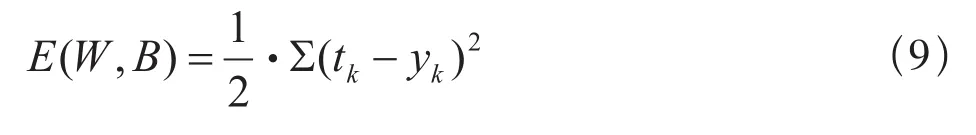
式（9）中，tk是期望的输出，yk为输出层的输出。

神经网络是研究重载列车驾驶曲线的重要组成部分，具体的神经网络模型建立流程如图1所示。

图1 神经网络模型建立流程

（1）采集适当足量的数据，对数据进行归一化处理。（2）分析确定研究重载列车模型适用条件如式（1）所示。（3）确定并选取线路限速、重载列车重量、列车长度、速度、坡度、前车位置、司机反应时间和列车制动减压目标值、列车缓解时间等参数作为神经网络模型的输入层和输出层的数据。（4）根据以上步骤中神经网络各层参数组成和要求构建对应的神经网络模型，确定其基本结构（7×11×2）。（5）利用训练数据样本采用L-BFGS拟牛顿法进行训练，直到满足精度要求，完成训练并保存神经网络。

在经过处理的样本中随机选取一定的样本作为神经网络的测试数据，神经网络测试数据的误差如图2所示。

1.3 驾驶曲线算法研究

具体的驾驶曲线研究过程如图3所示。

（1）判断列车是否满足模型适用条件，满足进行下一步，否则继续查询判断。

（2）实时采集并处理列车参数vlim（线路限速），j（线路坡度），G（重载列车重量），L（列车长度），v（列车速度），S（前车位置），t1（司机反应时间），r（制动减压目标值）和t2（缓解时间）。具体过程与训练样本归一化处理情况一致。其中，vlim、j、G、L当线路和列车确定后是确定值，v、S是在列车运行实时变化的，t1可根据经验获得。

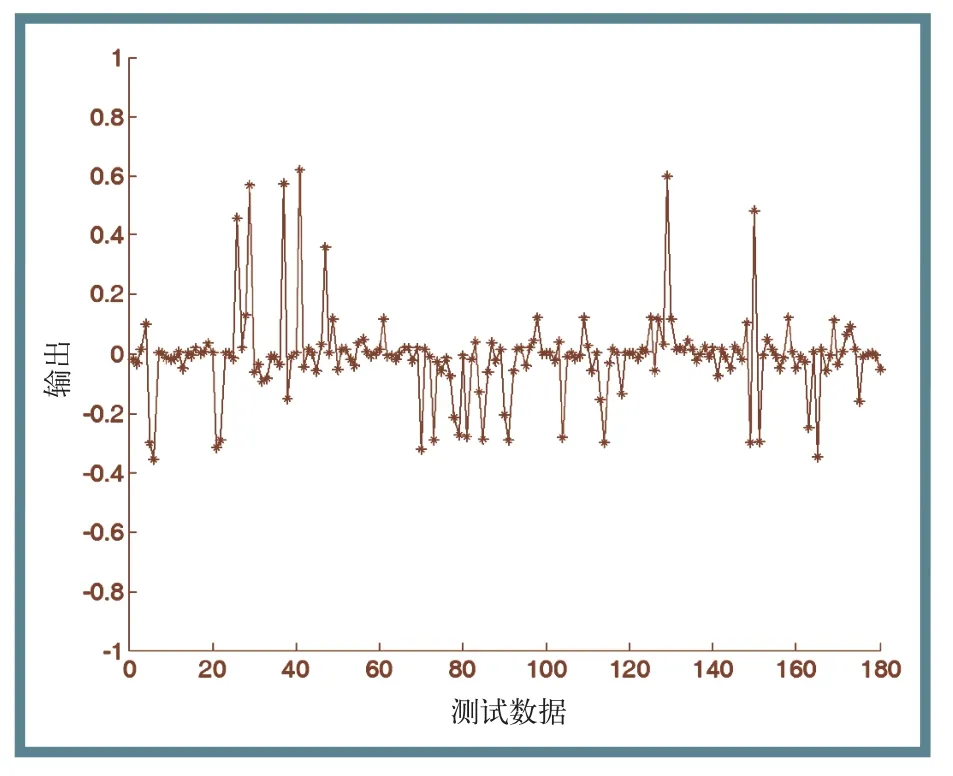
图2 神经网络测试数据误差

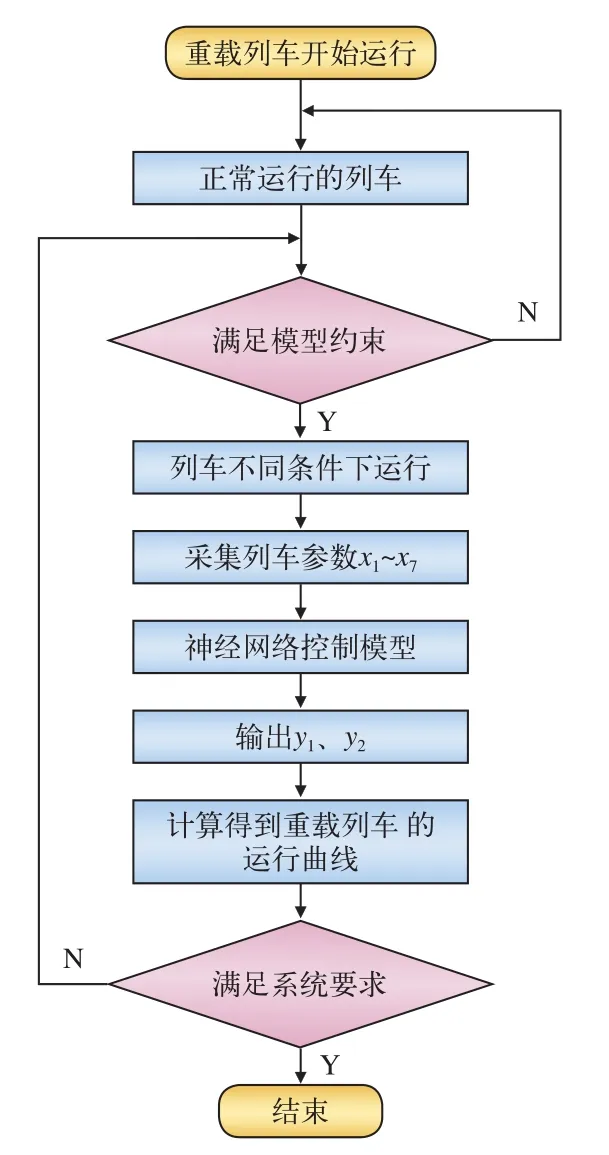
图3 基于神经网络的重载列车驾驶曲线研究

（3）将上一步中的数据作为输入数据输入到训练好的神经网络，输入参数x1～x7分别为：vlim、j、G、L、v、S、t1。

（4）获得相应输出y1，y2分别是r和t2的值并进行归一化处理。

（5）通过r和t2的值以及其它参数进行列车运动方程运算。机车牵引力与运行速度有关，取最大牵引力的90%；列车阻力由基本阻力、曲线附加阻力、坡道附加阻力以及隧道附加阻力构成；列车空气制动力通过闸瓦摩擦作用形成。其具体计算为：

式（10）中，Fmax是机车最大牵引力；ω0是列车单位基本阻力；ij是线路加算坡度千分数；θh是列车紧急制动换算制动率；βc是常用制动系数用于制动率取值；φh是换算摩擦系数。

列车紧急制时，βc=1 ；常用制动时与列车管定压和减压量有关如表1所示，将βc与列车换算制动率全值相乘，作为换算制动率。

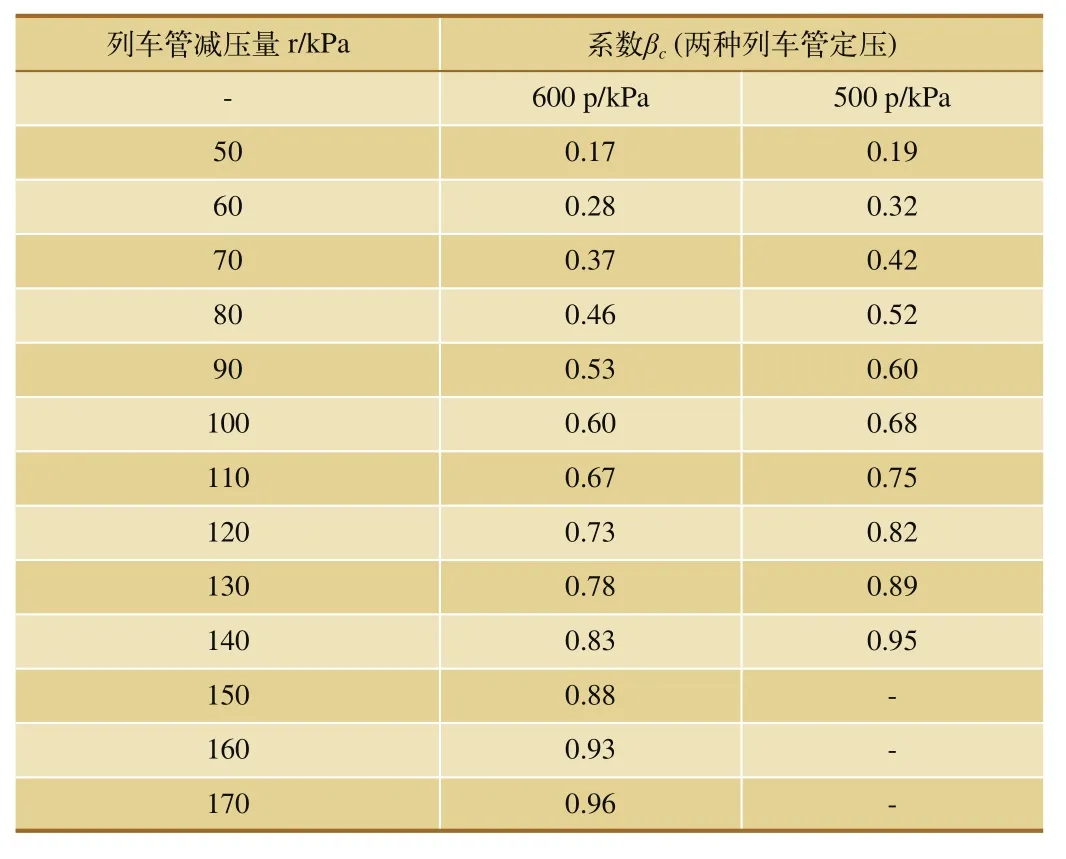
表1 常用制动系数βc取值表

列车制动时的走行距离可以表示为：

式（11）中，S为列车运行距离由空走距离Sk和有效制动距离Se组成；Sk表示列车从初速度v0制动开始到制动力起有效制动作用的时间tk内列车的运行距离；Se表示列车在制动力作用下减速运行的距离；速度v1、v2是减速运行的速度间隔。

（6）如果满足要求则此次运算结束，进入下一个周期的控制；否则重新循环。

在考虑上述情形时，综合重载列车运行过程中的约束条件：

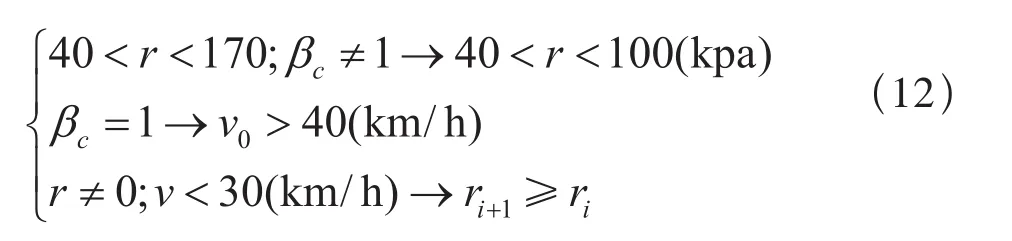
式（12）中，r表示空气制动时制动减压目标值，βc是常用制动系数，v0是制动初速度，v是列车运行速度，i和i+1表示前后两次制动减压。上式描述的条件是：列车有效减压目标值在40～170 kpa，重载列车非紧急制动情况下目标值一般不超过100 kpa；当列车紧急制动时，速度应不小于40 km/h；当列车制动速度低于30 km/h时，不允许列车管充风缓解。

2 仿真案例和结果分析

仿真实验采用MATLAB仿真软件编程实现，以某一段闭塞线路上运行的重载列车为研究对象，对该段线路上的重载列车运行过程进行神经网络仿真。该段线路仿真参数如表2所示。列车在该段线路运行时，采用以空气制动为主的制动方式，通常设置司机反应时间3.5 s，线路坡道参数如表3所示。

表2 系统仿真参数

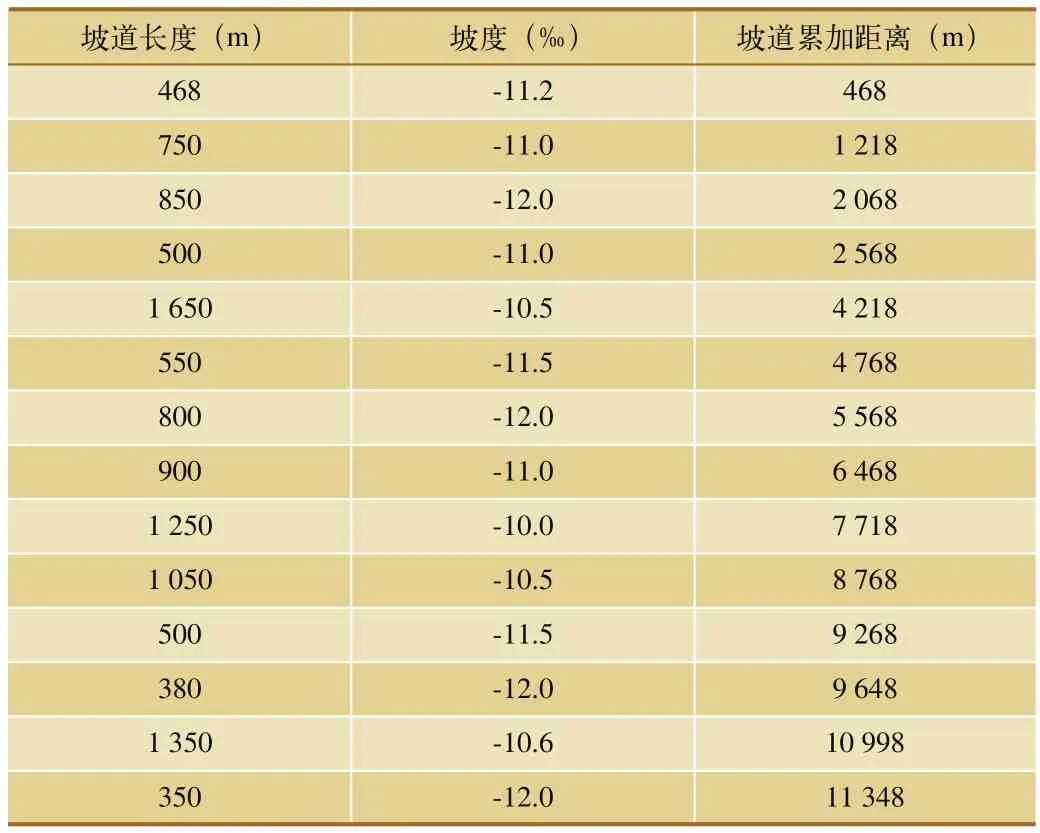
表3 实验线路坡道参数

对上述运行中的重载列车，当判断列车运行情况满足模型条件时，根据仿真参数和神经网络以及列车运动方程运算，得到重载列车运行仿真结果如图4所示。

图4 重载列车仿真结果与实际对比

驾驶曲线一与仿真运行速度差值的期望为1.458 4，方差为10.891 8，驾驶曲线二与仿真运行速度差值的期望为-0.432 7，方差为6.378。与图4对应的数据参数如表4所示。

表4 重载列车仿真运行数据

3 结束语

本文将重载列车运动方程及神经网络模型结合研究列车驾驶曲线。利用改进BP神经网络的非线性、简单特性进行重载列车制动运行建模，采用具有良好快速性和鲁棒性的L-BFGS训练算法，选择适当的训练样本和隐含层节点数。把列车空气制动减压目标值作为控制量，仿真得到重载列车驾驶曲线。

通过仿真结果与列车实际驾驶曲线对比可以看出，当列车在包含有连续长大下坡道的线路上运行时，仿真驾驶曲线可以较好的给出列车驾驶曲线，同时，根据相应的速度参数和制动及缓解动作可以看到仿真曲线与实际曲线具有相近的空气制动减压目标值和运行趋势，表明该方法是有效的。

[1]郜春海，陈德旺.基于模型选择和优化技术的自动驾驶制动模型辨识研究[J].铁道学报，2011，33（10）：57-60.

[2]董海荣，高 冰，宁 滨.列车自动驾驶调速系统自适应模糊控制[J].动力学与控制学报，2010，8（1）：87-91.

[3]Lijun Zhang，Xiangtao Zhuan，Xiaohua Xia.Optimal Operation of Heavy Haul Trains using Model Predictive Control Methodology[C].2011 IEEE International Conference on Service Operations and Logistics and Informatics (SOLI)，2011，402-407.

[4]董海鹰，刘 洋，李 欣，等.基于模糊神经网络预测控制的高速列车ATP研究[J].铁道学报，2013，35（8）：58-62.

[5]Khmelnitsky，E..On an optimal control problem of train operation[J].IEEE Transaction of Automatic Control，2000，45:1257-1266.

[6]Yufu Qin，Jun Peng，Xiaoyong Zhang.A Robust Fault Estimation Scheme for Heavy-haul Trains Equipped with ECP Brake Systems[C].2014 26th Chinese Control and Decision Conference (CCDC):2831-2836.

[7]M.T.Hagan，H.B.Demuth，M.H.Beale.Neural Network Design[M].Boston，MA:PWS，1996.

[8]S.Haykin.Neural networks a Comprehensive Foundation[M].Englewood Cliffs.NJ:Prentice-Hall，1999.

[9]P.R.Gill，W.Murray，M.H.Wright.The Levenberg-Marquardt method[M].Practical Optimization.London，U.K.:Academic，1981:136-137.

[10]D.E.Rumelhart，G.E.Hinton，R.J.Williams.Learning representations by back-propagating errors[J].Nature，1996(323):533-536.

[11]A.Bahar，C.Özgen，K.Leblebicioglu.Artificial neural network estimator design for the inferential model predictive control of an industrial distillation column[J].Ind.Eng.Chem.Res.,2004(43):6102-6111.

责任编辑 陈 蓉

Driving curve algorithm for heavy haul train based on improved BP Neural Network

TAN Litian,HUANG Youneng,LI Lingyu
( School of Electronic and Information Engineering,Beijing Jiaotong University,Beijing 100044,China)

This article proposed driving curve algorithm for heavy haul train (HHT) based on improved BP Neural Network (NN),used the actual train driving data for NN learning,described the nonlinear characteristics when the train braked,set the NN model of train braking operation process.The decompression target value of train braking and release time were used for the calculation of motion equation to obtain the driving curve for HHT.By comparing the curve with the real data from the Shuo-Huang Heavy Haul Line,the results showed that the method was effective.

heavy haul train (HHT);Neural Network (NN);simulation and modeling

U260.138∶TP39

A

1005-8451（2016）05-0001-05

2015-11-07

北京市科技计划项目（D151100005815001）；北京交通大学基本科研业务费资助项目（2015JBM013)；神华集团科技项目（20140269）。

谭力天，在读硕士研究生；黄友能，副教授。