基于基尼系数的电力网络投资分配模型及应用

张富强, 罗慧, 刘梅招, 高正平, 栗 楠, 文福拴

(1. 国网能源研究院, 北京市102209; 2. 国网江苏省电力公司,南京市 210024; 3. 江苏省电力公司电力经济技术研究院, 南京市 210008; 4. 浙江大学电气工程学院,杭州市 310027; 5. 文莱科技大学电机与电子工程系, 文莱斯里巴加湾市 BE1410)

基于基尼系数的电力网络投资分配模型及应用

张富强1, 罗慧2, 刘梅招2, 高正平3, 栗 楠1, 文福拴4,5

(1. 国网能源研究院, 北京市102209; 2. 国网江苏省电力公司,南京市 210024; 3. 江苏省电力公司电力经济技术研究院, 南京市 210008; 4. 浙江大学电气工程学院,杭州市 310027; 5. 文莱科技大学电机与电子工程系, 文莱斯里巴加湾市 BE1410)

将广泛应用于国民收入分配和环境治理领域的基尼系数引入电力网络投资分配方案设计中。首先,利用总资产回报率、未来给定时段内的预测售电量及投资售电比这3个指标, 在优先考虑效益(效率)的前提下, 综合确定电网公司未来的投资初始分配方案。然后, 选择容载比、可靠性等作为控制指标, 发展了基于基尼系数的投资分配模型, 并以投资初始分配方案为基础, 从提高分配公平性的角度优化确定最终的投资分配方案。最后, 对某省级电力网络进行实证研究, 证明所提投资分配模型的可行性。

电力网络; 投资分配; 基尼系数; 洛伦兹曲线; 控制指标

0 引 言

随着我国经济发展和人民生活水平不断提高, 人均电力消费量不断加大, 相应的电力网络投资规模也需要不断增大, 这对电网公司的投资决策提出了新的挑战。我国省级电网公司一般下设多个分公司,对这些分公司的投资进行适当管理是提高电网公司整体投资优化水平的前提。因此, 科学制定各分公司投资规模, 在提高投资效率的同时, 保障相关各地区电网发展水平相对均衡, 就成为亟待深入研究和解决的重要问题[1-9]。

基尼系数的提出最初是为了衡量国民收入分配的公平程度, 但该系数的实质是对分布均匀度的量化, 因此，可以将其应用到其他学科中与均匀度分析相关的多种问题[10-15]。文献[10]针对水污染负荷分配问题设计了基于基尼系数的模糊优化决策模型。文献[11]针对中国31个省(市、自治区)2010年的耕地现状, 建立了基于基尼系数的耕地保有量分配优化模型。文献[12]在电力系统调度问题中应用了基尼系数的概念。文献[13-15]在水污染负荷分配研究中运用了基尼系数的概念, 并做了实证分析, 对基尼系数的跨领域应用进行了论证。

本文首次将广泛应用于国民收入分配和环境治理领域的基尼系数概念引入到电力网络投资分配方案的设计中。首先利用各分公司的总资产利润率、未来给定时间段内预测增长售电量、综合投资售电比等指标, 以效益(效率)为优先考虑目标, 确定初始投资分配方案; 然后, 选择容载比、电力系统可靠性、安全供电(如“N-1”校验通过率)等控制指标, 采用基于基尼系数的投资分配模型, 从改善公平性的角度考虑, 以初始投资分配方案为基础优化得到最终的投资分配方案。

1 洛伦兹曲线与基尼系数

洛伦兹曲线由美国统计学家马克斯·洛伦兹提出, 用于研究国民收入在国民之间的合理分配问题。洛伦兹曲线将人口按收入由低到高进行排序, 以横轴和纵轴分别表示人口累计百分比和收入累计百分比, 计算任意累计百分比的人口所得到的收入累计百分比, 如图1中曲线LC。

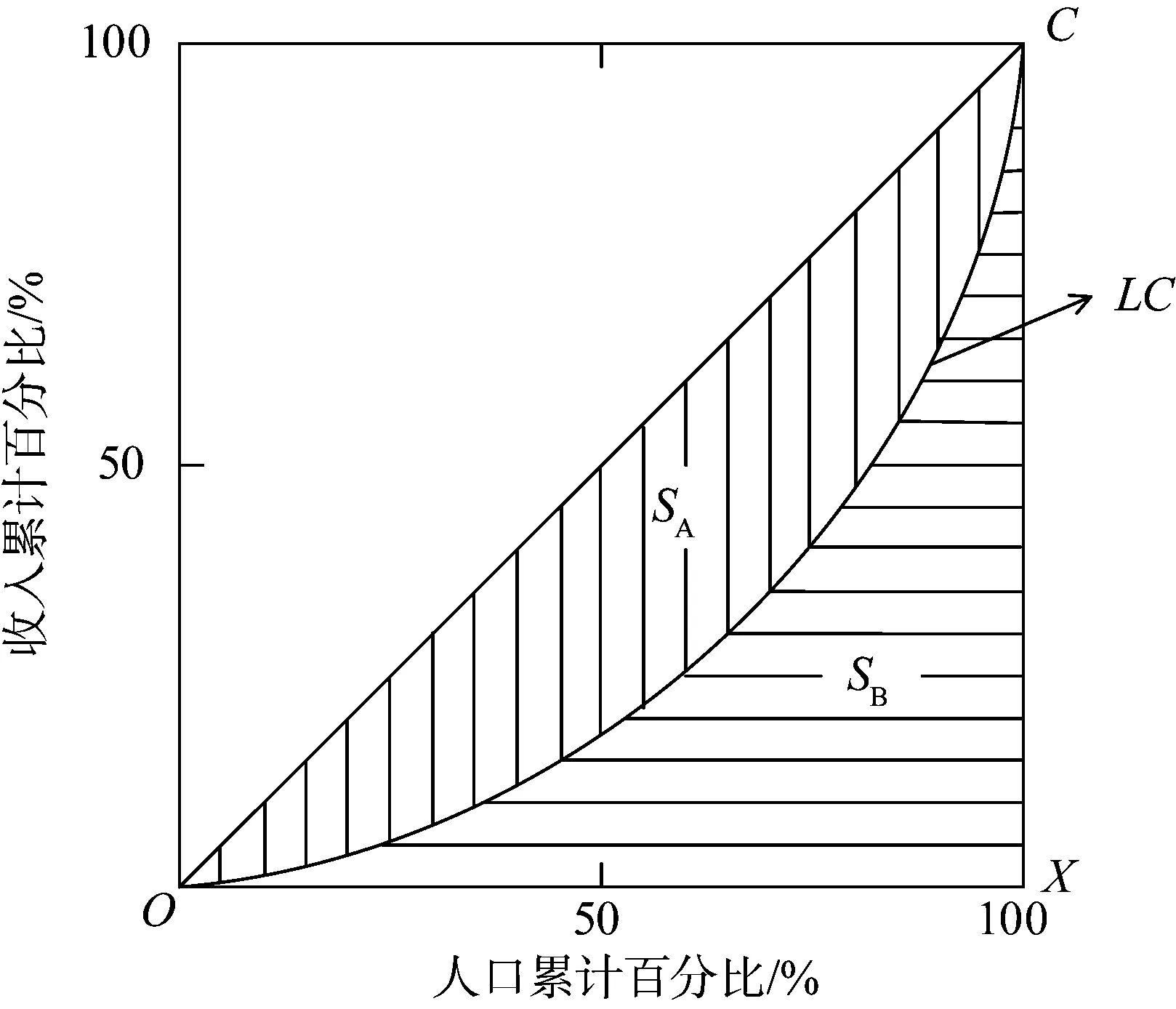
图1 洛伦兹曲线

基尼系数由意大利经济学家基尼提出,是根据洛伦兹曲线、绝对平等曲线和绝对不平等曲线定义的一个比值指标, 用于定量分析收入分配的不平等程度。

基尼系数G可由式(1)计算得到:

(1)

式中:SA表示收入分配绝对平等曲线OC与洛伦兹曲线LC之间围成的面积;SB表示洛伦兹曲线LC与收入分配绝对不平等曲线OXC之间围成的面积。

SA为0时,G为0, 表示收入分配完全平等;SB为0时，G为1, 表示收入分配绝对不平等。收入分配越趋于平等, 洛伦兹曲线LC的弧度越小, 基尼系数G也越小; 反之, 收入分配越趋于不平等,LC的弧度越大,G也越大。

国际上对用基尼系数衡量收入分配公平程度的通行规定见表1。

表1 基尼系数与收入分配公平程度的国际通行规定

Table 1 International provisions of Gini coefficient and fair income distribution degree

通常把基尼指数0.4作为收入分配差距的“警戒线”, 根据黄金分割律, 其准确值应为0.382。一般发达国家的基尼指数在0.24至0.36之间。

2 电网公司投资决策时需要考虑的重要因素

电网公司在确定未来投资方向时, 需重点考虑以下因素:(1) 已纳入国家电网公司规划的项目, 其所需投资要从省公司投资总额中扣除, 余下的投资才可以在下属地区间分配。(2) 满足无电地区用电需求。(3) 考虑企业效益，电网公司作为企业, 获得较高收益是企业的职能, 也是国资委对国有企业的要求。(4) 维持安全供电要求，要满足对可靠性要求高的地区或环节的特殊要求。(5) 满足新增负荷要求，考虑将投资向负荷增长率高的地区倾斜。

在上述5个因素中, 前2条是电网投资的硬性要求, 不存在优化空间。因此, 只能在后3个因素中选择合适的指标, 采用适当的优化方法, 确定下属分公司未来给定时期内的投资规模。

3 基于基尼系数的投资分配模型

本节将基尼系数引入电力网络投资分配问题中。 首先从效益的角度出发, 确立各分公司的初始投资计划。然后筛选出能够充分反映各地区满足供电情况的关键控制指标, 建立各指标的洛伦兹曲线并计算基尼系数。最后以基尼系数的加权和作为目标函数, 构建考虑多个约束条件的单目标规划优化模型, 通过设定合理的运算规则和采用适当的计算方法, 求得基尼系数相对较优的最终投资分配方案。这样确定的投资方案既反映了未来投资对分公司运行效率(效益)的影响, 又满足了经济发达地区对电力的需求, 同时兼顾了各个地区电力网络的平衡发展。

3.1 初始分配方案

采用反映经营效益的总资产回报率ROA,i、反映某地区未来增长潜力的给定时期的预测售电量Efore,i, 以及反映单位电量所需投资的综合投资售电比Rhis,i这3个指标, 来共同确定未来某地区/分公司i在某个给定时期内的电力网络投资初始分配方案。

由以上3个量可确定初始投资分配系数Sinit,i:

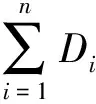
(2)

Di=ROA,iEfore,iRhis,i

(3)

式中n为相关地区或电力分公司数目。

3.2 基尼系数控制指标及其权重

针对地区电力网络投资分配问题, 基尼系数控制指标可从下述指标中选取: 220 kV容载比、城网110 kV容载比、重载变压器比例、轻载变压器比例、可靠性指标(停电小时数等)、“N-1”合格 (通过)率及电压合格率。本文采用熵权法确定各指标的权重。

假设mi表示第i个供电企业“十三五”期间的初始投资分配值;zji表示该供电企业i的第j个指标的实际值; 则该供电企业的第j个指标的单位投资额可表示为

yji=mi/zji

(4)

由此得到

(5)

式中pji表示第i个供电企业在第j个指标下所占比重。

(6)

式中ej表示第j个指标单位投资额的信息熵。

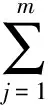
(7)

式中λj表示第j个指标的权重 (j=1, 2,…,m)，m表示指标数目。

3.3 绘制洛伦兹曲线

对于每个基尼系数控制指标, 可将其数值与初始方案分配系数相对应的斜率从小到大进行排序, 依次绘制洛伦兹曲线。以220 kV容载比为例, 首先计算各个分公司的单位容载比的投资额 (洛伦兹曲线图中各点的斜率, 即各分公司的新增投资/各分公司的容载比), 然后将所得数据从小到大排序, 并计算排序后各分公司的新增投资累积百分比和容载比累积百分比, 进而绘制各分公司新增投资和容载比的洛伦兹曲线, 如图2所示。

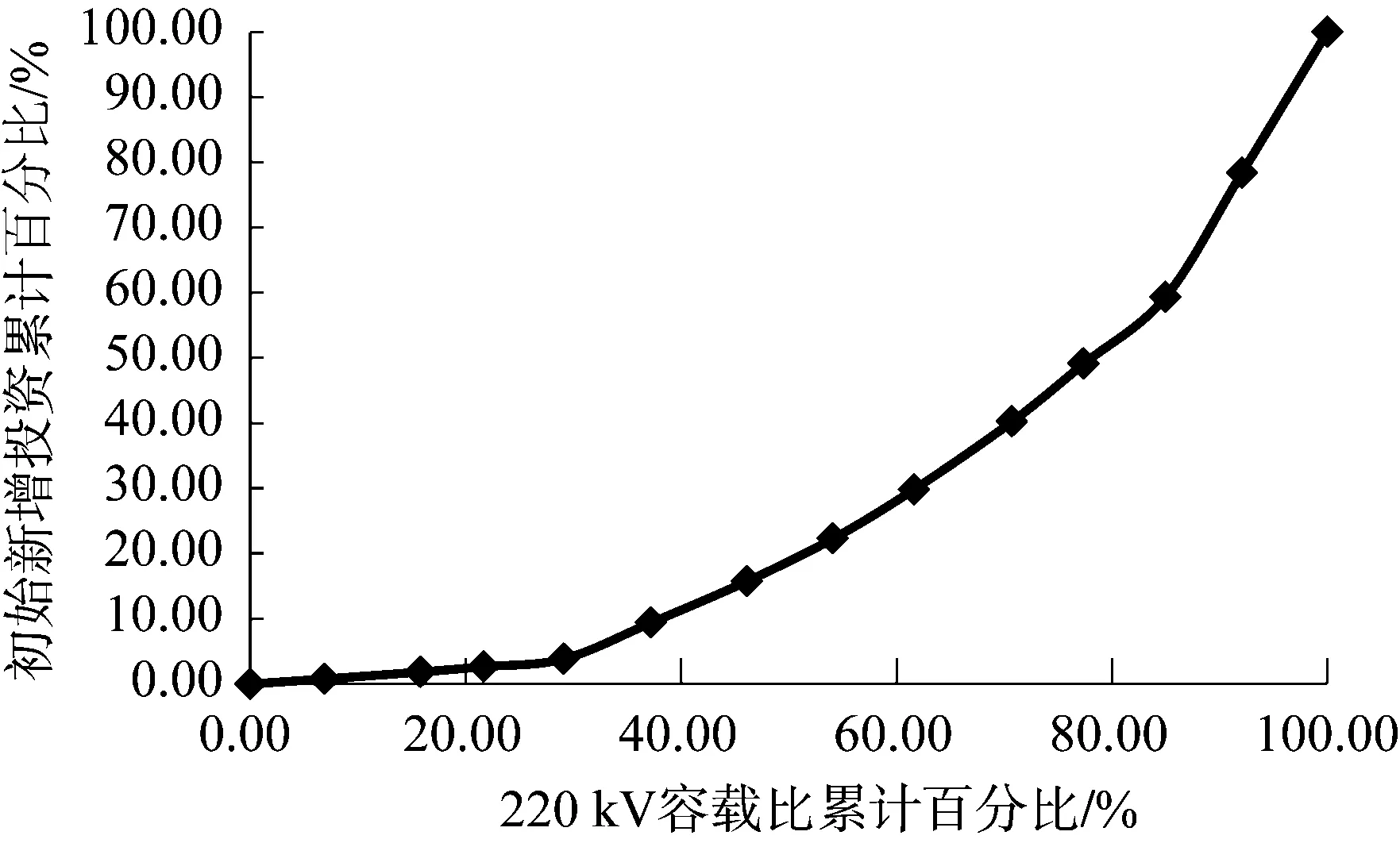
图2 220 kV容载比的洛伦兹曲线

同理, 也可绘出各分公司“十三五”新增投资额和其他基尼系数控制指标的洛伦兹曲线。

3.4 计算基尼系数

对每项基尼系数控制指标, 采用下梯形面积法计算其基尼系数, 计算公式为

(8)

式中:j为各个控制指标编号;i为分公司编号;Gj为基于某一控制指标j的基尼系数;Xj,i为指标j的累积百分比;Yj,i为基于指标j的投资分配量累积百分比; 当i=1时, (Xj,i-1,Yj,i-1)视为(0, 0)。

3.5 模型运算约束条件

在对模型进行运算时, 需施加一些约束条件, 以保证运算结果的合理性和实际可操作性。约束条件包括:(1) 调整后各控制指标对应的基尼系数小于或等于调整前的基尼系数, 即基于各指标的投资额分配公平性不能变差；(2) 单个分公司投资额调整幅度的限制；(3) 优化后每个基尼系数控制指标的洛伦兹曲线上各个分公司的排序不能发生变化。

3.6 求取最小基尼系数

在确定投资总量的分配方案时, 以各个控制指标的基尼系数加权和最小作为目标函数, 构造单目标、多约束优化模型。这样做的好处在于该优化模型存在唯一的最优解, 即最终的投资额分配方案为唯一最优方案。这就避免了以单一控制指标的基尼系数最小作为目标函数时可能导致的各个分公司间的利益争议和冲突。

目标函数:

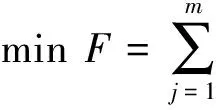
(9)

约束条件:

(1) 总投资额调整约束

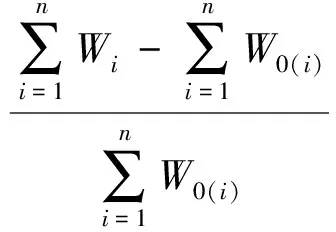
(10)

(2) 各控制指标现状基尼系数约束

Gj≤Gj(0)

(11)

(3) 各分公司分配额调整约束

pl≤Wi-Wi(0)≤ph

(12)

(4) 各分公司排序约束

(13)

Kj(i-1)≤Kj(i)≤Kj(i+1)

(14)

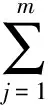
4 某省级电网投资分配实例分析

初始投资计划分配方案以总资产回报率、未来预测增长售电量、综合投资售电比(即单位电网投资增售电量的倒数)作为投资分配的基础。其中, 投资售电比意味着新增单位售电量所需的投资规模。在确定投资分配方案的过程中, 首先计算各分公司2011年到2014年的投资售电比, 之后给每年赋予不同的权值(为体现时间影响, 将2011—2014年的权重分别设置为0.1、0.2、0.3、0.4), 加权得到各分公司的综合投资售电比。综合考虑得到的投资售电比、总资产回报率和未来预测售电量, 可得到表2所示的电网投资初始分配方案。

表2 初始分配所采用指标数值及初始分配方案

Table 2 Idicators used in initial allocation and initial allocation scheme

这里选择数据质量较好的3个指标即220 kV容载比、城网停电时间、农网停电时间作为基尼系数控制指标对初始投资分配方案进行优化, 并采用熵权法得到这3个指标的权重分别为0.333, 0.304和0.363。在优化之前, 这3个控制指标的基尼系数分别为0.448，0.455，0.501, 考虑权重后的综合基尼系数为0.470。按照表1列出的标准, 该初始投资分配方案被归类为“差距较大”。

采用所提出的基于基尼系数的优化方法对初始投资分配方案进行调整。表3对初始投资分配方案和调整后的投资分配方案进行了比较。

与初始投资分配方案相比, 在调整后的投资分配方案中，3个控制指标和综合基尼系数都有一定程度的下降。3个控制指标即220 kV容载比、城网停电时间、农网停电时间的基尼系数在调整后的投资分配方案中分别为0.308，0.326，0.362, 综合基尼系数为0.333。按照表1列出的标准, 该优化调整后的投资分配方案被归类为“相对合理”。

以220 kV容载比为例, 对比优化前后的洛伦兹曲线，如图3所示。可以直观地看出, 优化后的洛伦兹曲线显然更接近绝对公平的分配曲线, 这表明在经过优化调整后的投资分配方案中，各关键指标及综合指标的分配公平性得到了一定程度的改善。

5 结 语

投资分配是电网公司发展规划、财务、运营监测等部门共同关注的重要问题。长期以来, 省级电力公司只有一个总的投资额度规划, 在地区分公司间应该怎样适当分配投资尚不存在广泛认同的方案, 也缺乏理论支撑, 这是一个值得研究的重要问题。

表3 优化前后的电力网络投资分配方案比较

Table 3 Comparisons between initial and adjusted investment allocation schemes

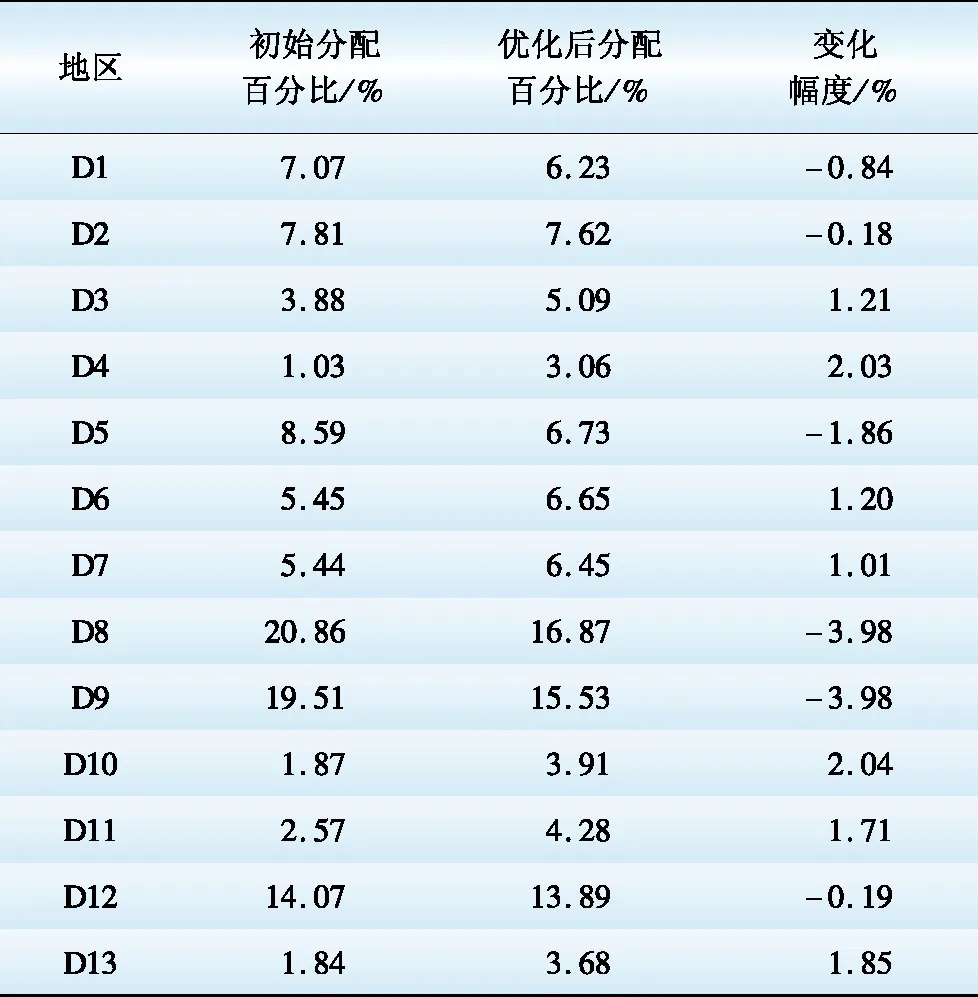
图3 在优化前后的投资分配方案中220 kV容载比的洛伦兹曲线

本文将基尼系数概念引入到对分公司投资分配方案的设计中, 建立了基于基尼系数的投资分配优化模型。这种方法以效益作为投资分配的基础, 并兼顾了投资分配的公平性, 得到的投资分配方案可以统筹兼顾各个地区电力网络的发展需求。最后, 用国内某省级电网公司的实际数据说明了所提模型与方法的可行性与有效性。

[1]崔巍, 都秀文, 杨海峰. 供电公司投资规模模型研究[J].电力建设,2013, 34(8): 27-33. CUI Wei, DU Xiuwen, YANG Haifeng. Investment scale model of power supply company[J]. Electric Power Construction, 2013, 34(8): 27-33.

[2]郑琳. 电网建设项目投资优化管理方法与应用[J]. 电力建设, 2011, 32(1): 104-107. ZHENG Lin. Optimal management method and its application in grid project portfolio[J]. Electric Power Construction, 2011, 32(1): 104-107.

[3]赵俊光, 雷波, 聂崇峡,等. 投资效益分析法在电网规划中的应用推广[J]. 电力建设, 2008, 29(10): 83-86. ZHAO Junguang, LEI Bo, NIE Chongxia, et al. Promotion of application of investment-benefit analysis in grid planning[J]. Electric Power Construction, 2008, 29(10): 83-86. [4]曾鸣, 韩蕊, 刘宏志,等. 无电地区电网投资风险识别及投资模式[J]. 电力建设, 2014, 35(02): 23-27. ZENG Ming , HAN Rui, LIU Hongzhi, et al. Risk identification and model of power grid investment in regions without electricity[J]. Electric Power Construction, 2014, 35(02): 23-27.

[5]崔巍, 崔莹莹, 杨海峰. 电网专项领域投资决策模型[J]. 电力建设, 2013, 34(10): 112-117. CUI Wei, CUI Yingying, YANG Haifeng. Investment decision model in special fields for power grid[J]. Electric Power Construction, 2013, 34(10): 112-117.

[6]张铁峰, 苑津莎, 郭伟. 基于数据包络分析的配电网投资项目经济评价[J]. 电力建设, 2005, 26(7): 68-70. ZHANG Tiefeng, YUAN Jinsha, GUO Wei. Economic Evaluation on distribution investment project by DEA[J]. Electric Power Construction, 2005, 26(7): 68-70.

[7]曾鸣, 王致杰, 刘珊珊,等. 无电地区电网建设项目投资效益后评价[J]. 电力建设, 2014, 35(5): 108-112. ZENG Ming, WANG Zhijie, LIU Shanshan, et al. Post-evaluation of investment benefit for grid construction project in regions without electricity[J]. Electric Power Construction, 2014, 35(5): 108-112.

[8]方略, 程浩忠, 柳璐,等. 基于多指标体系的10 kV配电网投资分配评价[J]. 华东电力, 2014, 42(6): 1092-1097. FANG Lue, CHENG Haozhong, LIU Lu, et al. evaluation of 10 kV distribution Network investment allocation based on multi-index system[J]. East China Electric Power, 2014, 42(6): 1092-1097.

[9]董军, 马博. 考虑社会效益的电网最优投资组合模型研究[J]. 运筹与管理, 2010, 19(4): 131-135. DONG Jun, MA Bo. Study of optimal portfolio model for electric grid projects with social benefits[J]. Operation Research and Management Science, 2010, 19(4): 131-135.

[10]李如忠, 舒琨. 基于基尼系数的水污染负荷分配模糊优化决策模型[J].环境科学学报, 2010, 30(7): 1518-1526. LI Ruzhong, SHU Kun. Fuzzy optimization model for waste load allocations based on the Gini coefficient[J]. Acta Scientiae Circumstantiae, 2010, 30(7): 1518-1526.

[11]张琳, 陈逸, 张群, 等. 基于基尼系数的耕地保有量分配优化模型[J]. 经济地理, 2012, 32(6): 132-137. ZHANG Lin, CHEN Yi, ZHANG Qun, et al. Optimization model for cultivated land allocations based on the Gini coefficient[J]. Economic Geography, 2012, 32(6): 132-137.

[12]戴俊良, 王鹏, 王轩, 等. 基于基尼系数的电力调度公平性指标探讨[J]. 电力系统自动化, 2008, 32(2): 26-29. DAI Junliang, WANG Peng, WANG Xuan, et al. Discussion on impartiality index of power dispatching based on Gini coefficient[J]. Automation of Electric Power Systems, 2008, 32(2): 26-29.

[13]BURN D H, LENCE B J. Comparison of optimization formulations for waste-load allocations[J]. Journal of Environmental Engineering, 1992, 118(4): 597-612.

[14]王丽琼. 基于公平性的水污染物总量分配基尼系数分析[J]. 生态环境, 2008, 17(5): 1796-1801. WANG Liqiong. Analysis of total pollutant load allocation for water bodies Gini coefficient based on equity[J]. Ecology and Environment, 2008, 17(5): 1796-1801.

[15]BURN D H, MCBEAN E A. Optimization modeling of water quality in an uncertain environment[J]. Water Resources Research, 1985, 21(7): 934-940.

张富强 (1982), 男, 博士, 高级工程师, 研究方向为能源战略、电力规划与电力市场；

罗慧 (1979), 女, 硕士, 高级会计师, 研究方向为企业经营管理；

刘梅招(1983)，女，博士，高级工程师，研究方向为电力市场、电力技术经济分析；

高正平(1976)，男，博士，高级工程师，研究方向为电力技术经济分析、采购与供应链管理；

栗楠(1986)，女，博士，工程师，研究方向为主动配电网规划与分析；

文福拴 (1965), 男, 教授, 博士生导师, 研究方向为电力系统故障诊断与系统恢复、电力经济与电力市场、智能电网与电动汽车等。

(编辑 张小飞)

A Gini Coefficient Based Investment Allocation Model for Power Networks and Its Application

ZHANG Fuqiang1, LUO Hui2, LIU Meizhao2, GAO Zhengping3, LI Nan1, WEN Fushuan4,5

(1. State Grid Energy Research Institute, Beijing 102209, China;2. State Grid Jiangsu Electric Power Company, Nanjing 210024, China; 3. Jiangsu Electric Power Company Econominc Research Institute, Nanjing 210008, China; 4. School of Electrical Engineering, Zhejiang University, Hangzhou 310027,China; 5. Department of Electrical and Electronic Engineering, Brunei Institute of Technology, Bandar Seri Begawan BE1410, Brunei)

This paper introduces the Gini coefficient widely used in the national income allocation and environmental governance into the investment allocation scheme design of power network. Firstly, we use three indexes including the return on total assets, future forecasted electricity consumption in a given period and the ratio between investment and electricity sale, to determine the initial allocation scheme of future investment in a given power network under the premise of preferentially considering the efficiency/benefits. Then, we choose capacity-load ratio, reliability and other control indexes to develop the investment allocation model based on the Gini coefficient. And we determine the final optimal investment allocation scheme from the perspective of improving the allocation fairness, based on the initial allocation scheme of future investment. Finally, a provincial power company is taken as an example to demonstrate the feasibility of the proposed investment allocation model.

power network; investment allocation; Gini coefficient; Lorenz curve; control index

国家自然科学基金项目(51477151, 51361130152)

TM 715

A

1000-7229(2016)01-0009-06

10.3969/j.issn.1000-7229.2016.01.002

2015-10-22

Project supported by National Natural Science Foundation of China (51477151, 51361130152)