基于自回归模型和相位斜率指数的动态脑连接分析

黄 亮 吴超华 高小榕

(清华大学医学院生物医学工程系，北京 100084)

基于自回归模型和相位斜率指数的动态脑连接分析

黄 亮 吴超华 高小榕#*

(清华大学医学院生物医学工程系，北京 100084)

随着脑网络理论的发展，人们越来越关注不同脑区域之间的功能性和效应性连接。在常见的脑活动无创检测方法中，脑电图(EEG)具有较高的时间分辨率，适于进行效应性连接分析。提出一种估计不同通道的EEG信号间的效应性连接的方法，即自回归相位斜率指数(AR-PSI)。该方法结合多元自回归(MVAR)模型对短时数据进行谱估计频率分辨率高的特点和相位斜率指数(PSI)对源信号混叠不敏感的特点。与传统的格兰杰因果模型相比，它可以有效地摒除由于容积导体效应造成的信号混叠所带来的干扰；与传统的PSI相比，它在短时数据上能够更准确地估计不同通道间EEG信号的效应性连接。首先，分别生成具有强效应性连接和相互独立的混叠噪声这两组信号进行模拟实验，结果表明AR-PSI方法确实能够更有效地检测出信号中存在的效应连接，排除信号线性混叠可能引起的误检。然后，应用此方法并结合滑动窗技术，对Stroop实验记录到的EEG数据进行网络连接的动态分析，发现250～500 ms和550～800 ms时间段内脑网络连接密度在两种条件下存在显著性差异。分析结果，显示语义和颜色不一致条件的刺激能够引起脑网络连接密度更迅速地增加，且连接跨度更大。

效应性连接；MVAR模型；相位斜率指数(PSI)；动态分析

引言

近年来，脑网络理论[1-8]越来越受到人们的关注，产生了大量的研究成果。要构建一个脑网络，关键步骤之一是如何定义节点与节点之间的连接。根据研究方法的不同，脑连接可以分为结构连接[9]、功能连接[10]和效应连接[11]三大类。结构连接描述不同脑区在物理上的联系，目前常用的主要是通过解剖和医学影像技术观察和计算不同大脑区域的物理连接或者形态相似性；功能连接表示不同大脑区域的功能活动在时间上的统计相关性，目前主要是根据脑电图(EEG)、脑磁图(MEG)和功能核磁共振(fMRI)测量的信号来进行统计计算；效应连接则反映不同脑区之间的有向信息传输机制，估计效应连接需要的数据与估计功能连接所用的数据基本相同，不同之处主要在于连接的统计计算方法上。目前，计算效应连接的方法大多是基于参数模型的方法，包括结构方程模型、多变量回归模型、动态因果模型、格兰杰因果模型等。

格兰杰因果(Granger-causal, GC)模型[12]是目前比较常用并且比较成熟的估计变量间因果关系的方法，在基于脑电信号的效应连接分析中也占有一席之地。该方法的基本思想是：如果加入第二个变量的信息能够使对第一个变量的预测更加准确，那么就认为第二个变量是第一个变量的因。但是，在实际的多通道头皮脑电信号采集中，由于容积导体效应，所观察到的脑电信号实际上是多个活动源信号混叠的结果，GC模型在应用于此类信号时，就会估计出虚假的效应连接。基于此，Nolte等提出了相位斜率指数(phase slope index，PSI)[13]。该方法基于多通道信号的交叉谱相位，利用其相位的斜率，能够确定不同频率带上信号的时间先后关系，从而确定信号之间的效应连接。后来，Haufe等通过仿真实验对GC和PSI进行了较为严格的评估，证明PSI在避免因信号混叠引起的虚假效应连接估计方面确实有较强的优势[14]。实际上，PSI方法计算的准确性与多通道信号交叉谱频率分辨率密切相关。Nolte等采用一般的非参数方法估计多通道信号的交叉谱，当数据长度较短时，估计所得谱的频率分辨率低，使实际计算出的PSI值准确度降低。为了克服这个问题，本研究提出了自回归相位斜率指数(autoregressive phase slope index，AR-PSI)。该方法通过引入多元自回归模型(MVAR)[15]，把MVAR和PSI方法的优势结合起来，能更加准确有效地估计EEG信号各个通道之间的效应连接。

1 方法和实验

1.1 AR-PSI方法

AR-PSI方法实际上是AR模型和PSI方法的结合，它充分利用了AR模型谱估计频率分辨率高的优势和PSI方法对源信号混叠不敏感的特点，能够更准确地估计多通道信号之间的效应连接，下面将详细论述AR-PSI方法的原理和步骤。

1.1.1 MVAR模型拟合

MVAR是AR模型在多维变量上的扩展。通常，MVAR模型可以用方程表示为

(1)

式中：xn∈m表示m维平稳时间序列；A1,A2,…,Ap∈m×m是MVAR模型的系数矩阵;un表示均值为零、协方差矩阵为Σ∈m×m的不相关噪声向量；v∈m是非零均值时间序列的截距项。

为了方便计算，通常在对时间序列进行去均值处理后，把截距项设为零。因此，MVAR模型实际需要估计的未知参数就只是Ak和Σ。

有文献报道了多种MVAR模型的参数估计方法(即模型拟合方法)，包括最小二乘类方法(如MLS、ARFIT[16]及LWR[17])、点阵类方法(如Vieira-Morf[18])、状态空间模型类方法(Kalmanfiltering[19])等，这些方法的性能可参考文献[20]。在这些方法中，MLS方法(多维最小二乘法)最为简单，而且性能不差，所以本研究采用此方法进行MVAR模型的拟合。

在MVAR模型拟合之前，需要指定模型的阶数p。阶数的选择与模型的拟合效果有密切关系：阶数选得过小，不足以充分利用观测数据的信息进行准确拟合；阶数选得过大，需要估计的未知量增多，容易出现过拟合，且估计所需计算量也大大增加。一般情况下，可以使用一种或多种准则来选择模型阶数，常用的准则包括SBC(Schwarz-Bayescriterion)准则、AIC(Akaikeinformationcriterio)准则、FPE(Akaike′sfinalpredictionerror)准则和HQ(Hannan-Quinncriterio)准则等[15]。对于小样本数据来说，AIC准则和FPE准则具有更好的效果[15]。本研究的实验数据样本量有限，所以选用AIC准则[21]进行阶数选择，该准则的计算公式为

(2)

式中，Σ(p)表示p阶模型拟合误差的协方差矩阵，N表示用于模型拟合的总数据点数。

MVAR模型拟合完成之后，需要对该模型进行统计上的检验，以确保拟合的结果是可信的。通常，检验内容包括3个方面：拟合度检验、稳定性检验和一致性检验。

拟合度检验旨在检验拟合系数矩阵是否完全描述了原始数据的内部关联结构，该检验等效为检验拟合系数矩阵用于原始数据上所得残差是否是白噪声。一般的做法是：检验一定迟滞h以内的残差自相关系数是否足够小，以确保在一定置信水平上不能拒绝残差是白噪声的假设。在多变量自回归模型的拟合验证中，采用混成检验法(portmanteautests)[22]得到的结果更加可信。混成检验法定义了一系列的检验统计量，这些统计量包括Box-Pierce(BPP)、Ljung-Box(LBP)、Li-Mcleod(LMP)等，它们在残差是白噪声的零假设下近似服从自由度为m2(h-p)的χ2分布。选用其中一个统计量LMP，表示为

(3)

式中，Cl表示迟滞l时的残差自相关系数。

稳定性检验即检验系统是否能够收敛，可以通过判断系数矩阵构成的稳定性矩阵的特征值是否都在单位圆内来实现。稳定性矩阵的结构为

(4)

稳定指数可定义为

(5)

式中，λmax是稳定性矩阵A绝对值最大的特征值。当SI<0时，该MVAR模型是稳定的。

一致性检验即判断真实数据拟合结果和拟合得到的模型重新生成的仿真数据拟合结果的相似程度。Ding等[23]定义了一致性百分比指数的计算式，即

(6)

式中，Rr和Rs分别表示真实数据和由拟合模型产生的模拟数据的自相关矩阵。

PC值越接近于100%，表明拟合模型越能够产生和原始数据具有相同关联结构的数据。

1.1.2 相干谱估计

一旦拟合的模型通过上述检验，就可以在此基础上进行相干谱估计。对式(1)的两边同时进行傅里叶变换，把MVAR模型转换为频域形式，可得

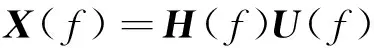
(7)

式中，H(f)被称为系统转移方程，其定义如下：

(8)

据此，很容易得到其谱矩阵，有

(9)

式中，H*(f)是H(f)的共轭转置。

以此方法得到的谱分辨率高，不受计算样本数据长短的限制。传统的非参数方法为保证谱的频率分辨率需要更长的数据，所以当数据长度有限时，用MVAR模型的方法比用传统非参数方法能够得到更精细的谱分析结果，有利于更精确地计算PSI。

1.1.3PSI估计

PSI基于相干谱相位的斜率，定义如下：

(10)

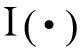
归一化的相干谱定义如下：

(11)

通过适当的变换，式(10)可以写成如下便于理解的形式，有

(12)

当该相位谱的频率分辨率足够高时，有

(13)

因此，PSI实际表示的是相干谱相位斜率的加权平均，权系数为各个频率上的归一化相干谱幅度。

从PSI的定义来看，PSI取得的是相干谱的虚部，而相干谱的虚部信息并不会因为源信号之间的混叠而发生变化[24]。所以，PSI能够有效地避免源信号混叠所带来的效应连接误估计。从式(13)可以看出，δf越小(频率分辨率越高)，等式左右越趋近于相等，PSI值越准确。在传统的PSI估计方法中，运用非参谱估计方法得到的谱频率分辨率受信号长度限制，而笔者采用MVAR模型进行谱估计，大大提高了相干谱的频率分辨率，能够更准确地估计出PSI。

1.2 仿真实验

为了证实AR-PSI方法在测量不同信号之间的效应连接方面的优越性，首先将该方法在一些仿真数据上进行测试。仿真数据包括两组二维的时间序列，每组的采样点数均为2 000点，采样率为100 Hz。其中一组数据是用如下所示的一阶MVAR模型生成的，即

(14)

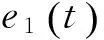
另一组是相互独立的白噪声和粉红噪声的线性混叠，即

(15)

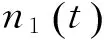
对仿真信号先进行分段，每段长度为400点，然后分别用GC方法、PSI方法和AR-PSI方法对信号间的效应连接进行估计。按照上述方法生成2000组仿真信号，求取3种指标的平均值和方差，如图1(c)、(d)所示。

从图1所示的结果中可以看出：对于有强效应连接的两个信号(MVAR模型生成的仿真信号)，3种方法都比较好地估计出了信号间的效应连接，但是AR-PSI方法估计结果的均值显著大于其他两种方法(配对t检验，P<0.5)，而其估计结果的方差也显著小于其他两种方法(F检验，P<0.5)。结果表明，对于实际存在效应连接的信号，AR-PSI方法能够估计出更大且更稳定的结果。而对于线性混叠的独立噪声信号，GC方法误检出了效应连接，其结果显著大于0(t检验，P<0.5)，传统PSI方法和AR-PSI方法估计结果的均值没有显著性差异(配对t检验，P=0.28)，但是，AR-PSI方法估计结果的方差却显著小于传统PSI方法的方差(F检验，P<0.5)。结果表明，AR-PSI方法能够最有效地消除效应连接的误检，且比传统PSI方法更稳定。综上所述，在参与比较的3种方法中，AR-PSI方法能够更有效地检测出信号中存在的效应连接，排除信号线性混叠可能引起的误检。

图1 数据仿真实验。 (a)二维一阶AR模型生成的信号；(b) 相互独立的白噪声与粉红噪声混叠的信号；(c) GC方法、PSI方法和AR-PSI方法分别对(a)中信号估计所得效应连接的均值和方差；(d) GC方法、PSI方法和AR-PSI方法分别对(b)中信号估计所得效应连接的均值和方差Fig.1 Simulation results. (a) Signal generated by 2 dimensional 1 order AR model; (b)Mixture signal of independent white and pink noise; (c) Effective connectivity estimated by Granger Causality, PSI, AR-PSI using data (a). The height of the bar indicates the mean and the error bar indicates the standard deviation; (d) Effective connectivity estimated by Granger Causality, PSI, AR-PSI using data (b). The height of the bar indicates the mean and the error bar indicates the standard deviation

1.3 真实EEG信号的动态脑连接分析

仿真数据上的实验，证明了AR-PSI方法相对GC方法及传统PSI方法在估计脑效应连接上的优越性。接下来，结合滑动窗技术和AR-PSI方法，利用真实EEG信号进行动态脑连接分析。

1.3.1 数据采集

真实EEG数据是在汉字语义颜色Stroop实验[25]中采集到的数据。该实验包含语义和颜色一致、语义和颜色不一致以及语义和颜色无关3种刺激条件，每一例受试在3种条件下各采集得到120个试次的EEG数据。实验阶段共采集了15例受试，其中第14例受试信号受眼电污染严重，信号极不平稳，所以没有进行分析。在实验时，受试位于密闭的屏蔽室，采用Synamps2 (Neuroscan Inc.)脑电系统，记录60个通道的脑电数据，电极位置如图2所示。采样率为1 000 Hz，以头顶为参考。

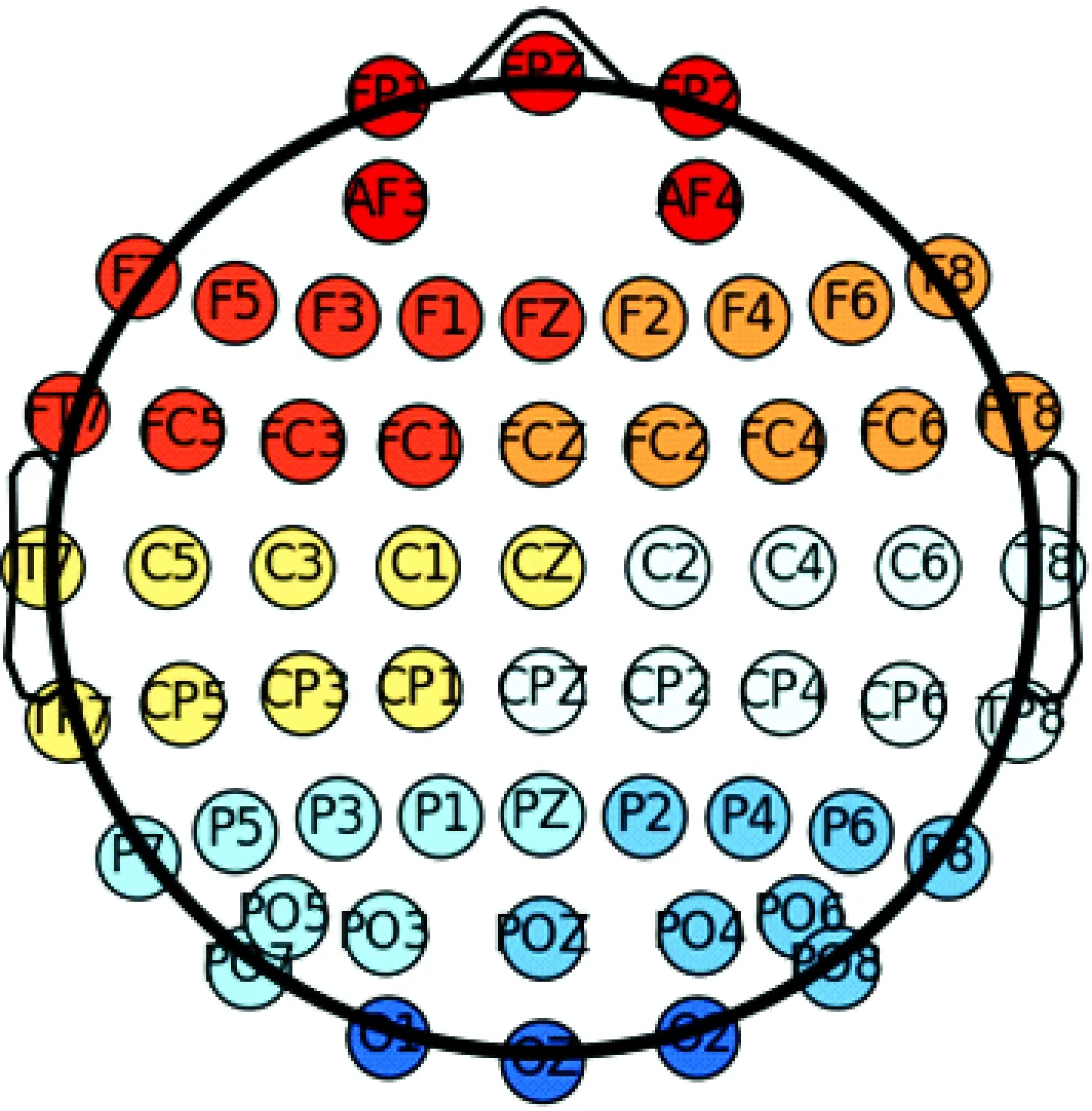
图2 电极位置及分区Fig.2 Electrodes position and subarea

为了方便后续的分析，对这60个电极进行分区，并用不同的色彩标识。其中，FP1、FPZ、FP2、AF3、AF4这5个电极定义为F区域(前额叶区)，F7、F5、F3、F1、FZ、FC1、FC3、FC5、FT7这9个电极定义为LF区域(左侧额叶区)，F2、F4、F6、F8、FT8、FC6、FC4、FC2、FCZ这9个电极定义为RF区域(右侧额叶区)，T7、C5、C3、C1、CZ、CP1、CP3、CP5、TP7这9个电极定义为LC区域(左侧中央区)，C2、C4、C6、T8、TP8、CP6、CP4、CP2、CPZ这9个电极定义为RC区域(右侧中央区)，P7、P5、P3、P1、PZ、PO3、PO5、PO7这8个电极定义为LP区域(左侧顶叶区)，P2、P4、P6、P8、PO8、PO6、PO4、POZ这8个电极定义为RP区域(右侧顶叶区)，O1、OZ、O2这3个电极定义为O区域(枕叶区)。*该分区只是为了方便描述而对电极进行的粗略分区，它们与解剖上的大脑分区并不一定存在严格的一一对应关系。

1.3.2 数据预处理

在进行分析前，实验采集的原始EEG数据都需要经过特定的预处理过程,主要分为以下两大步骤。

1)第一大步骤的预处理过程。预处理的目的在于获取可用于脑连接分析的数据源：首先，进行1～40 Hz的带通滤波，消除漂移噪声和高频噪声；其次，降采样到200 Hz，其目的在于增强数据的平稳性以适于进行MVAR模型拟合；再次，截取刺激前1 200 ms到刺激后1 000 ms的数据用作分析。经过这3项处理，每一例受试和每一种条件都分别得到一个60×440×120(通道数×数据点数×试次数)的EEG数据矩阵，这便是后续进行脑连接分析的数据源。

2)第二大步骤的预处理过程[23]。采用AR-PSI方法进行脑连接分析，一个很重要的步骤就是MVAR模型的拟合，而MVAR模型拟合必须保证数据源在时间上的平稳性。实际上，带有ERP的EEG信号却包含非平稳成分，因此笔者通过第二大步骤的预处理过程来提高数据的平稳性。首先，对上一步骤获得的数据源进行归一化处理，即减去其时域平均值，并除以其时域标准差，保证每一试次和每一通道的信号幅度近似一致；其次，去除信号中的ERP成分(非平稳成分)，即用上述处理后的信号减去其总体平均。经过这两步处理后，还可以用矩形窗截取小段数据，因为数据越短，其平稳性越好。在有多个试次的情况下，即使是只有小段数据，MVAR模型也能够较好地拟合其模型参数。经过试验，窗长为250 ms时，数据能够比较好地进行MVAR模型的拟合。为了连续地观察不同时间段内脑连接的变化情况，还引入了滑动窗技术，窗长为250 ms(即50个数据点)，窗滑动步长为50 ms(即10个数据点)。

1.3.3 脑连接估计

经过以上预处理之后，每个短窗中的数据都可用于MVAR模型的拟合。首先，根据AIC准则选择一个合适的模型阶数。通过设定模型阶数依次为1～20，根据式(2)计算出每一阶数对应的AIC值，可得到一条单调下降的曲线。该曲线显示，随着模型阶数的增长，AIC值逐渐下降，并且其下降速率也逐渐减小，经过某个比较明显的拐点之后，AIC值就趋于平稳。对于每一段窗数据，都能够得到类似的曲线，其拐点基本上都位于阶数10左右。为了保持对所有数据处理方法的一致，方便之后做不同条件和不同时间下的结果对比，对所有窗中的数据都采用60个变量的10阶MVAR模型进行拟合。

完成模型拟合之后，采用多变量混成检验方法，检验由各个窗数据的拟合模型得到的剩余噪声是否为白噪声。在剩余噪声为白噪声的原假设条件下，应用替代数据法构造随机的1 000例剩余噪声样本，并依据式(3)分别计算每一个样本的Li-McLeod统计量，就可以得到该统计量的一个分布，在此分布的基础上计算P值。经过计算，对于各段窗数据MVAR拟合模型的统计检验结果都有P>0.05，因而可判定在统计意义上这些拟合模型的剩余噪声均为白噪声。

同时，根据式(5)、(6)验证各拟合模型的稳定性和一致性。稳定性矩阵A绝对值的最大特征值的对数值均小于0，说明估计得到的模型都是稳定的;模型一致性的计算结果也均在70%左右，可以认为具有良好的一致性。综合其检验结果，可以判定各个窗数据拟合得到的MVAR模型均能够很好地反映原始数据的内在结构，这些拟合结果是可信的。

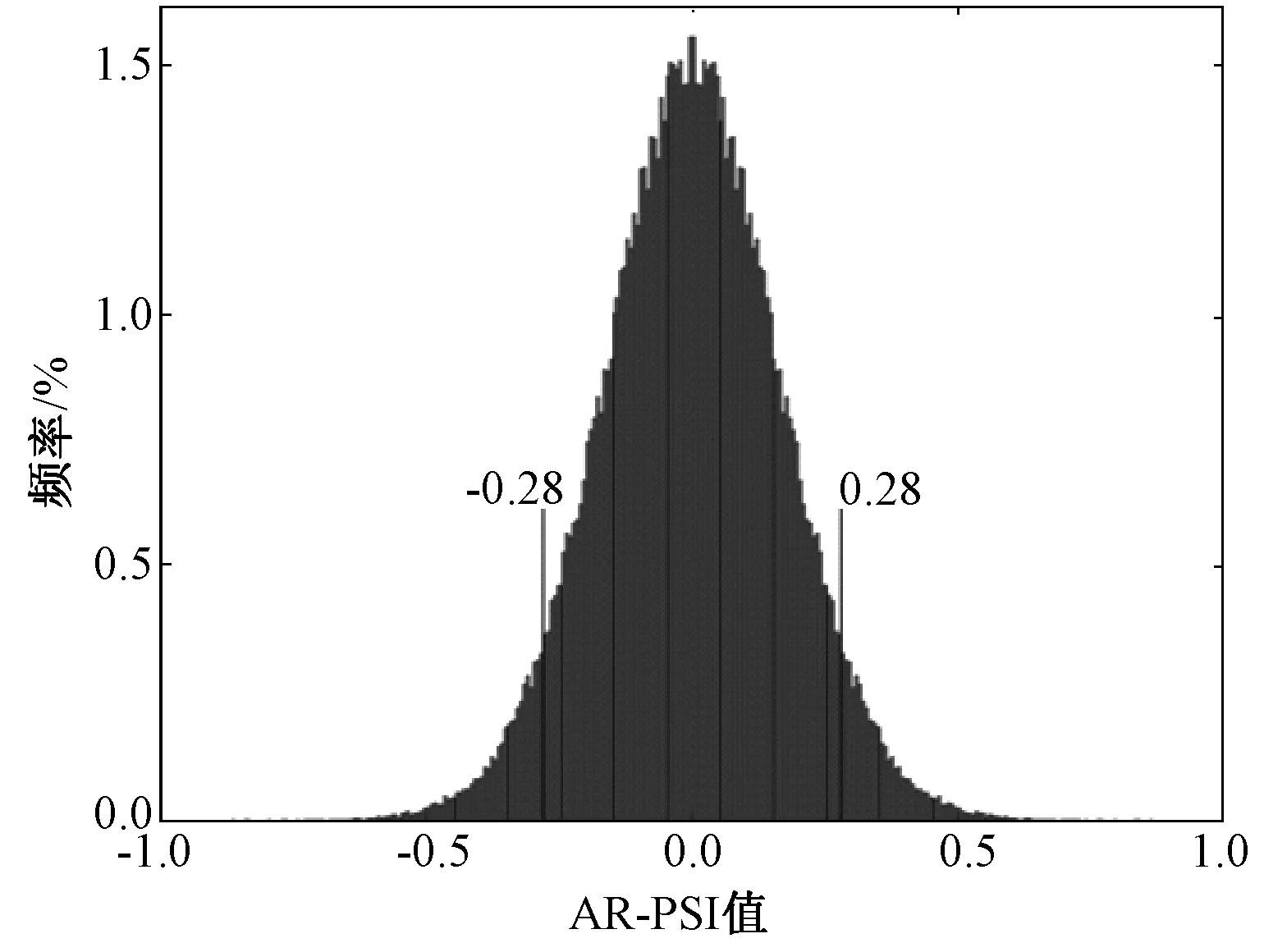
图3 两种条件及不同时间段AR-PSI值统计直方图Fig.3 Histogram of AR-PSI value in all time windows and conditions

1.3.4 脑连接分析

AR-PSI描述的是不同信号之间的因果联系，所以其值有正有负，而得到的也是一个个有向网络。基于图理论的复杂网络有许多分析指标，选取网络连接密度，其定义式为

(16)

式中，E表示网络的边数，V表示网络的节点数。

网络连接密度与网络平均度意义等同，可反映当前脑网络的连接数，间接反映当前脑活动的强弱。

统计各个时间段所构建的平均脑网络的连接密度，并采用t检验的方法对两种条件之间进行统计检验，找出存在显著性差异的时间段。然后，对于存在显著性差异的时间段的脑网络，根据前面所划分的8个区域，统计这些区域之间的连接方向和连接数，并利用重采样的方法对两种条件之间进行统计检验。最后，计算脑网络各区域的出度(本区域节点是其他区域节点因的连接总数)和入度(其他区域节点是本区域节点因的连接总数)，进一步分析脑网络中的信息流向。

2 结果

为了验证Stroop实验数据的可靠性，给出了FCZ通道平均后的ERP波形，如图4(b)所示。可以发现，两种条件下的ERP波形在400～600 ms这个时间段内存在显著性差异(逐点配对t检验，P<0.05)，且不一致条件下的波形比一致条件下的波形小，与已有文献的研究结果相符[26，28]，表明所采集到的数据是可靠的。

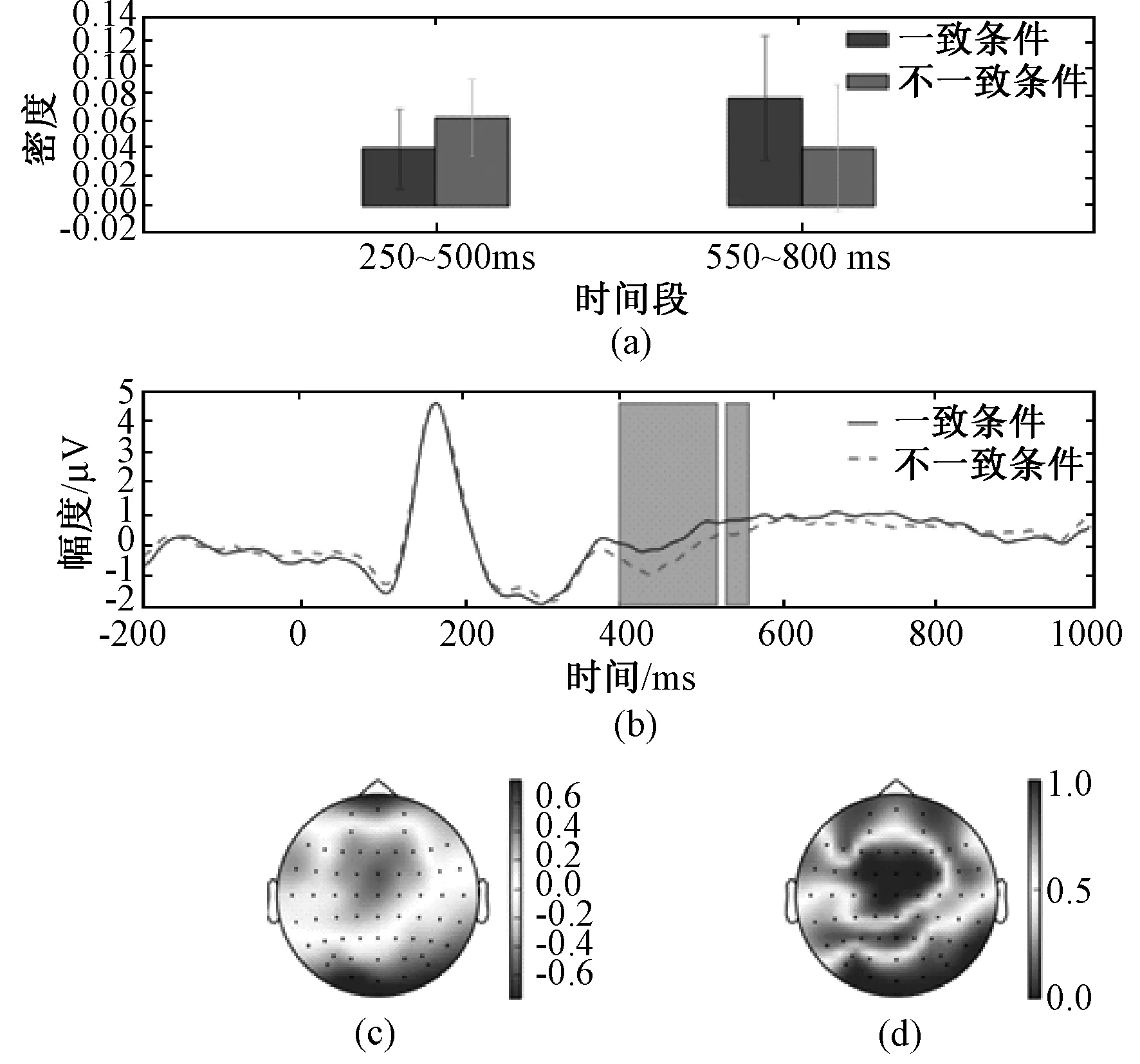
图4 脑连接动态分析。 (a) 两种条件下有显著性差异时间段的脑网络连接密度；(b) 两种条件下FCZ电极的受试平均ERP波形(绿色覆盖部分表示两种条件下ERP波形存在显著性差异的时间段)；(c) “语义与颜色”一致条件和不一致条件ERP差值在显著性差异的时间段内均值的空间分布；(d) “语义与颜色”一致条件和不一致条件ERP配对t检验P值的空间分布Fig.4 Dynamic brain connectivity analysis. (a) Connectivity density with significant difference under two conditions; (b) Grand averaged ERP at electrode FCZ under two conditions (The region covered by green rectangle is the period with significant difference under two conditions); (c) Topographic map of the mean of ERP difference between two conditions in the periods with significant difference; (d) Topographic map of P value computed by pairwise t test

两种条件下的脑网络连接密度在250～500 ms (配对t检验，P=0.047)及550～800 ms (配对t检验，P=0.011)时间段有显著性差异，见图4(a)。刺激发生之后，两种条件下的脑网络连接密度均呈上升趋势。从两个有显著性差异的时间段来看，在250～500 ms时间段内，不一致条件下的脑网络连接密度显著高于一致条件下的脑网络连接密度，而在550～800 ms时间段内，一致条件下的脑网络连接密度反而显著高于一致条件的脑网络连接密度。

两种条件下脑网络连接密度存在显著性差异，其时间段的网络连接如图5所示。图中节点表示的是EEG信号采集的各个通道，每个节点上都标有对应通道的标号；连接表明两个节点区域存在效应连接，连接的一端加粗指示连接的方向性，即未加粗的一端影响加粗的一端。节点按照前后左右脑上的电极通道分别排布在圆圈的上下左右，区域与电极通道的对应关系用不同的色彩标出。从图5可以直观地看出，在连接方向上，不一致条件下主要是从LF区域(左侧额叶区)指向RP区域(右侧顶叶区)，而一致条件下主要是从RF区域(右侧额叶区)指向LC区域(左侧中央区)、RP区域(右侧顶叶区)指向RF区域(右侧额叶区)和LP区域(左侧顶叶区)。

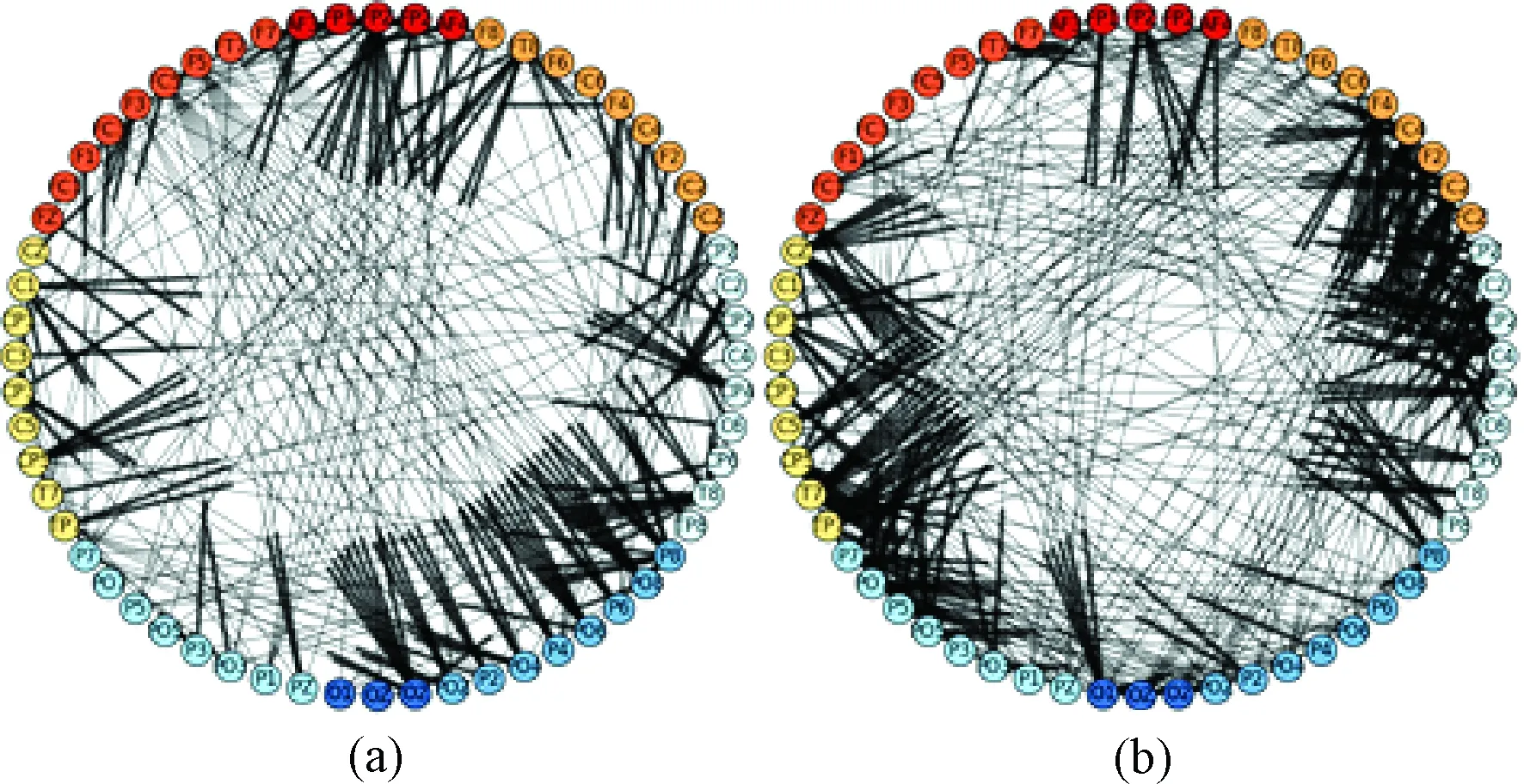
图5 脑网络图。 (a) 250～500 ms时间段内“语义与颜色”不一致条件下构建的脑网络图，网络密度显著大于对应时间段内“语义与颜色”一致条件下构建的脑网络图；(b) 550～800 ms时间段内“语义与颜色”一致条件下构建的脑网络图，网络密度显著大于对应时间段内“语义与颜色”不一致条件下构建的脑网络图Fig.5 Brain network. (a) Brain network under incongruent condition at 250-500ms, whose density is larger than that under congruent condition at the corresponding period. (b) Brain network constructed under congruent condition at 550-800ms, whose density is larger than that under incongruent condition at the corresponding period

对区域之间的连接方向和连接数进行统计，得到两种条件下存在显著性差异的脑区域连接分布，如图6所示。在250～500 ms时间段内，不一致条件下LF区域(左侧额叶区)指向RP区域(右侧顶叶区)的连接数远远多于其他区域之间的连接数(见图6(a))；在550～800 ms时间段内，一致条件下RP区域(右侧顶叶区)指向RF区域(右侧额叶区)以及RP区域(右侧顶叶区)指向LP区域(左侧顶叶区)相对于其他区域之间存在较多的连接(见图6(b))。

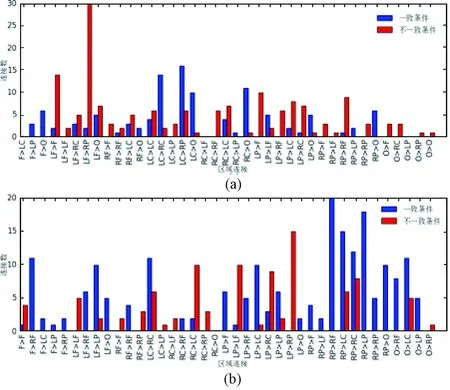
图6 脑区域连接分布。 (a)250～500 ms时间段两种条件下脑连接数具有显著性差异的脑区域连接分布；(b)550～800 ms时间段两种条件下脑连接数具有显著性差异的脑区域连接分布Fig.6 Brain connectivity between different areas. (a) Brain connectivity between different areas with significant difference under two conditions in 250～500 ms; (b) Brain connectivity between different areas with significant difference under two conditions in 550～800 ms

表1 250～500 ms及550～800 ms时间段不同条件下各脑区域的出度和入度统计

Tab.1 Out-degree and in-degree of different brain areas under two condition in 250～500 ms and 550～800 ms

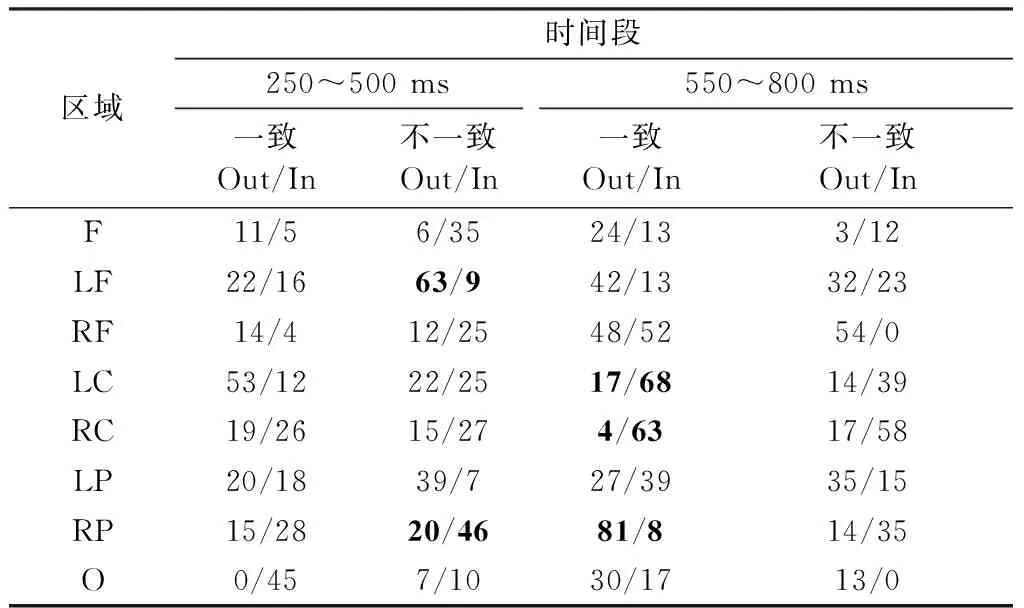
区域时间段250～500ms550～800ms一致Out/In不一致Out/In一致Out/In不一致Out/InF11/56/3524/133/12LF22/1663/942/1332/23RF14/412/2548/5254/0LC53/1222/2517/6814/39RC19/2615/274/6317/58LP20/1839/727/3935/15RP15/2820/4681/814/35O0/457/1030/1713/0

计算脑网络各区域的出度和入度，得到表1所示结果。首先重点关注250～500 ms的不一致条件，结果显示从LF区域(左侧额叶区)信息流出最多，而RP区域(右侧顶叶区)信息流入最多，相对于该时间段内的一致条件下，LF区域(左侧额叶区)与RP区域(右侧顶叶区)有更强的效应连接，文献[29]也得出左额叶脑区与顶叶脑区在不一致条件下有更强相干性的结论。然后，再考察550～800 ms的一致条件，发现信息流出最多的区域是RP区域(右侧顶叶区)，信息流入最多的是LC区域(左侧中央区)，RC区域(右侧中央区)的信息流入量次之。两者对比可以发现，不一致条件下大脑前后方向的大跨度信息流动偏多，而一致条件下小跨度信息流动偏多，并且倾向于左右方向之间的流动。文献[30-31]报道称，Stroop效应主要是前扣带皮层(ACC)活动差异引起的，不一致条件下ACC区域活动增强，并同时影响脑前额叶和其他区域，因而使得脑前后连接增强，与本研究结果有一定的相似性。

3 讨论

对于上述数据现象，结合人脑对信息的加工机理以及Stroop效应的自动化模型[32]加以讨论。Stroop效应的自动化模型认为：人脑对语义和颜色的加工采用不同的方式，对语义是自动加工，对颜色是控制加工，当语义和颜色不一致时，语义信息的自动加工会对颜色信息的控制加工产生干扰，产生Stroop效应。于是，可以做这样的推测：当干扰发生时，大脑可能需要立刻调用更多、更广范围内的资源协同来对这种干扰进行排除，因而在该条件下脑网络连接数迅速增加，并且主要表现在前后脑大跨度的连接增多；而当语义和颜色一致时，对于两者的处理不会产生相互干扰，大脑遵循正常的信息处理模式，调用的资源可能是逐步增加，因而脑网络连接数是持续缓慢地增加，并且主要表现为小跨度的连接模式。同时，笔者也注意到，连接性有显著性差异的时间段和ERP信号波形有显著性差异的时间段并不完全一致。脑电连接性和ERP信号所反映的认知神经过程并不完全一致，它们可能存在时间上的先后关系。但是，根据本研究的实验和数据并不能做出准确的推测，因此将在今后对此开展更为细致的研究。

本研究所提出的AR-PSI方法在估计效应连接的准确性方面相比GC方法和传统PSI方法确实有一定的优势。进一步地，如果以该方法为依托能够针对短时数据有效地构建起脑网络，将会有利于进行动态分析。但是，该方法在数据量很大的情况下，计算起来比较耗时。一方面，MVAR模型拟合花费大量时间；另一方面，利用MVAR模型系数在全频率段估计PSI，由于伴随着大量的矩阵求逆运算也相当耗时。所以，该方法在计算速度上比不上可以直接在时域进行运算的GC方法。因此，该方法更适合用于对实时性要求不高的离线分析场合。

另外，脑电信号应用脑网络分析时，不同的参考选择对其分析结果也有着不同的影响[33-34]。虽然AR-PSI方法能够很好地消除容积导体效应的影响，但是却不能消除参考电极的影响。由于篇幅所限，本研究在应用AR-PSI方法进行脑网络构建时，直接选择头顶作为参考，没有进一步考虑其他的参考可能会给脑网络分析的结果带来何种影响，这也将会是后续研究工作中的一个重要方向。

4 结论

本研究利用MVAR模型在多通道信号谱估计方面频率分辨率高的优势，并结合PSI方法，对独立源信号混叠的不敏感性提出了AR-PSI来估计不同通道EEG信号之间的效应连接，从理论上分析了它的可行性以及存在的优势。仿真结果也显示，相比GC方法，它可以有效地防止由于信号混叠造成的虚警；相比传统PSI方法，它能更准确地估计效应连接。在研究中，将AR-PSI应用于Stroop实验采集的EEG数据，并基于AR-PSI进行了动态脑连接分析。分析结果显示，语义和颜色不一致条件的刺激能够引起脑网络连接密度更迅速地增加，并且连接跨度更大，表明大脑在处理具有冲突的信息时可能会更快地调动更多、更广泛的资源。

(致谢 本课题得到清华大学医学院神经工程实验室老师和同学的大力支持，分析所用Stroop实验数据来源于清华大学神经工程实验室高文静同学，在此一并表示感谢。)

[1] Sporns O, Tononi G, Kötter R. The human connectome: a structural description of the human brain[J]. PLoS Computational Biology, 2005, 1(4): e42.

[2] 蒋田仔, 刘勇, 李永辉. 脑网络：从脑结构到脑功能[J]. 生命科学, 2009(2):181-188.

[3] 梁夏, 王金辉, 贺永. 人脑连接组研究：脑结构网络和脑功能网络[J]. 科学通报, 2010(16): 1565-1583.

[4] 孙俊峰, 洪祥飞, 童善保. 复杂脑网络研究进展——结构、功能、计算与应用[J]. 复杂系统与复杂性科学, 2011, 7(4): 74-90.

[5] Bullmore E, Sporns O. The economy of brain network organization[J]. Nature Reviews Neuroscience, 2012, 13(5): 336-349.

[6] Van Essen DC, Smith SM, Barch DM, et al. The WU-Minn human connectome project: an overview[J]. Neuroimage, 2013, 80: 62-79.

[7] Sporns O. Making sense of brain network data[J]. Nature Methods, 2013, 10(6): 491-493.

[8] Uehara T, Yamasaki T, Okamoto T, et al. Efficiency of a “small-world” brain network depends on consciousness level: a resting-state FMRI study[J]. Cerebral Cortex, 2014, 24(6): 1529-1539.

[9] Koch MA, Norris DG, Hund-Georgiadis M. An investigation of functional and anatomical connectivity using magnetic resonance imaging[J]. Neuroimage, 2002, 16(1): 241-250.

[10] Fingelkurts AA, Fingelkurts AA, Kähkönen S. Functional connectivity in the brain—is it an elusive concept?[J]. Neuroscience & Biobehavioral Reviews, 2005, 28(8): 827-836.

[11] Horwitz B. The elusive concept of brain connectivity[J]. Neuroimage, 2003, 19(2): 466-470.

[12] Handbook of Time Series Analysis: Recent Theoretical Developments and Applications[M]. New York: John Wiley & Sons, 2006.

[13] Nolte G, Ziehe A, Nikulin VV, et al. Robustly estimating the flow direction of information in complex physical systems[J]. Physical Review Letters, 2008, 100(23): 234101.

[14] Haufe S, Nikulin VV, Müller KR, et al. A critical assessment of connectivity measures for EEG data: a simulation study[J]. Neuroimage, 2013, 64(1):120-133.

15] Lütkepohl H. New Introduction to Multiple Time Series Analysis[M]. Berlin: Springer Science & Business Media, 2007.

[16] Schneider T, Neumaier A. Algorithm 808: ARfit—A Matlab package for the estimation of parameters and eigenmodes of multivariate autoregressive models[J]. ACM Transactions on Mathematical Software (TOMS), 2001, 27(1): 58-65.

[17] Morf M, Vieira A, Lee DTL, et al. Recursive multichannel maximum entropy spectral estimation[J]. IEEE Trans Geosci Electron, 1978, 16(2): 85-94.

[18] Marple Jr SL. Digital Spectral Analysis with Applications[M]. Englewood Cliffs: Prentice-Hall, 1987.

[19] Schlögl A. The Electroencephalogram and the Adaptive Autoregressive Model: Theory and Applications [M]. Aachen: Shaker, 2000.

[20] Schlögl A. A comparison of multivariate autoregressive estimators[J]. Signal Processing, 2006, 86(9): 2426-2429.

[21] Akaike H. A new look at the statistical model identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716-723.

[22] Hosking JRM. The multivariate portmanteau statistic[J]. Journal of the American Statistical Association, 1980, 75(371): 602-608.

[23] Ding M, Bressler SL, Yang W, et al. Short-window spectral analysis of cortical event-related potentials by adaptive multivariate autoregressive modeling: data preprocessing, model validation, and variability assessment[J]. Biological Cybernetics, 2000, 83(1): 35-45.

[24] Nolte G, Bai O, Wheaton L, et al. Identifying true brain interaction from EEG data using the imaginary part of coherency[J]. Clinical Neurophysiology, 2004, 115(10): 2292-2307.

[25] 高文静, 陈小刚, 高小榕. 基于 Hermite 滤波器的稳态视觉诱发电位背景标记 Stroop 效应包络分析[J]. 中国生物医学工程学报, 2014, 31(1): 1-7.

[26] Qiu J, Luo Y, Wang Q, et al. Brain mechanism of Stroop interference effect in Chinese characters[J]. Brain Research, 2006, 1072(1): 186-193.

[27] Liotti M, Woldorff MG, Perez R, et al. An ERP study of the temporal course of the Stroop color-word interference effect[J]. Neuropsychologia, 2000, 38(5): 701-711.

[28] Zysset S, Müller K, Lohmann G, et al. Color-word matching Stroop task: separating interference and response conflict[J]. Neuroimage, 2001, 13(1): 29-36.

[29] Schack B, Chen ACN, Mescha S, et al. Instantaneous EEG coherence analysis during the Stroop task[J]. Clinical Neurophysiology, 1999, 110(8): 1410-1426.

[30] Harrison BJ, Shaw M, Yücel M, et al. Functional connectivity during Stroop task performance.[J]. NeuroImage, 2005, 24(1):181-191.

[31] Hanslmayr S, Pastötter B, Bäuml KH, et al. The electrophysiological dynamics of interference during the stroop task[J]. Journal of Cognitive Neuroscience, 2008, 20(2):215-225.

[32] MacLeod CM. Half a century of research on the Stroop effect: an integrative review[J]. Psychological Bulletin, 1991, 109(2): 163-203.

[33] Marzetti L, Nolte G, Perrucci MG, et al. The use of standardized infinity reference in EEG coherency studies[J]. Neuroimage, 2007, 36(1):48-63.

[34] Yun Q, Peng X, Yao D. A comparative study of different references for EEG default mode network: the use of the infinity reference.[J]. Clinical Neurophysiology, 2010, 121(12):1981-1991.

Dynamic Brain Connectivity Analysis Based on Autoregressive Model and Phase Slope Index

Huang Liang Wu Chaohua Gao Xiaorong#*

(DepartmentofBiomedicalEngineering,MedicalSchool,TsinghuaUniversity,Beijing100084,China)

Functional and effective connectivity are important branches in brain network research. Electroencephalogram (EEG) has sufficient temporal resolution to catch the fast brain dynamic changes, so it is suitable for effective connectivity analysis. We proposed a new method to estimate the effective connectivity base on EEG, namely autoregressive phase slope index (AR-PSI). Spectral estimation based on MVAR has high frequency resolution even on short time data. PSI is insensitive to linear mixture of non-interacting sources. AR-PSI combined advantages of the two methods. Compared with conventional Granger causality model, AR-PSI could eliminate the interference caused by volume conduction. Compared with conventional PSI, AR-PSI could get more accurate estimation of effective connectivity with short time data. Experimental data indicated that AR-PSI could exactly detect the effective connectivity between two signals and exclude the false detection. AR-PSI was also applied to dynamic brain connectivity analysis based on EEG recorded in Stroop paradigm. We found that brain connectivity density had significant difference under two conditions in 250～500 ms and 550～800 ms. The results indicated that the incongruent stimulus could make the density of brain network increase more quickly and expand the span of connectivity.

effective connectivity; MVAR model; phase slope index( PSI); dynamic analysis

10.3969/j.issn.0258-8021. 2016. 01.001

2015-06-03， 录用日期:2015-09-16

国家自然科学基金重点项目(61431007, 91320202, 91220301)

R318

A

0258-8021(2016) 01-0001-09

# 中国生物医学工程学会会员(Member, Chinese Society of Biomedical Engineering)

*通信作者(Corresponding author)， E-mail: gxr-dea@tsinghua.edu.cn