基于MOGA算法的W型金属封严环结构优化设计

丁相玉

摘 要：目前航空发动机内的工作温度越来越高，导致传统密封所使用的非金属密封圈不能满足发动机的使用要求。本文首先利用ANSYS有限元软件对影响W型金属封严环力学性能的环外臂张开角度以及环外臂凸段圆弧角度进行了分析，得出了在环外臂张开角度取1.398°～14.156°之间及环外臂凸段圆弧角度取30.21°～59.5°之间时，封严环的力学性能能够满足使用要求。随后利用MOGA优化算法有限元方法对W型金属封严环进行优化设计，得出在环外臂张开角度取3.39°及环外臂凸段圆弧角度取32.18°时封严环为最优设计。

关键词：封严环；MOGA优化算法；外臂张开角度；外臂凸段圆弧角度

0 引言

目前航空发动机内的工作温度越来越高，导致传统密封所使用的非金属密封圈不能满足发动机的使用要求[1]。而用金属封严环取代非金属密封圈，能有效地解决高温腐蚀环境下的辅助密封问题。但封严环因其“薄壁、大变形、精密”于一体，研制难度极大，设计分析影响因素众多，目前只有少数发达国家掌握其核心的设计、加工技术，我国在该领域尚未有完整系统的设计分析和制造体系，有必要系统深入研究[2]。本文利用ANSYS有限元分析软件，建立了轴对称截面W型金属封严环的有限元模型，利用ANSYS Workbench Direct Optimization模块的MOGA优化算法（多目标遗传算法）来对封严环结构参数进行优化，以获得W型金属封严环的相关设计和优化的规律。

1 封严环材料

选用强化镍基高温合金GH4169[3，4]作为封严环的材料。该材料的最高工作温度为650℃以上。其塑性、疲劳性能、断裂韧性、抗氧化性等性能很好，在高温下的强度也很高。材料的基本力学性能参数见表1[5]。

2 优化参数的确定

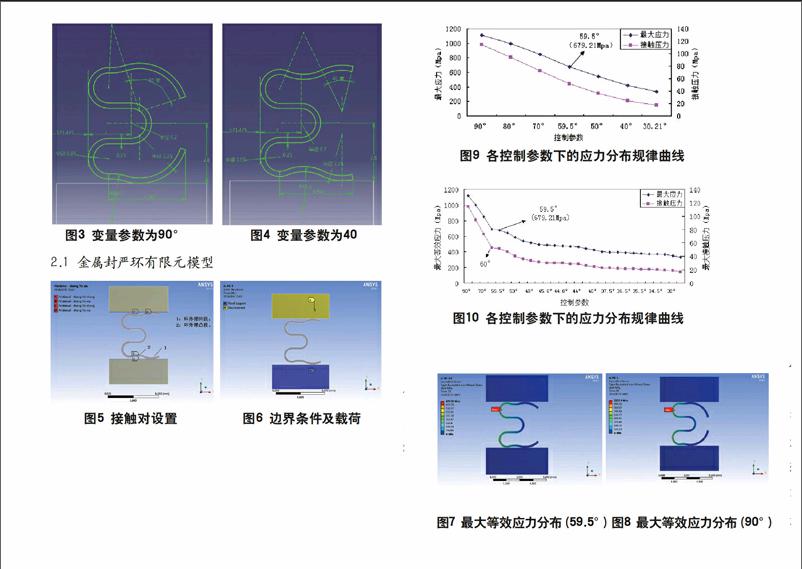
本文利用给定的W型金属封严环模型，其内径R1=371.48mm，外径R2=376.01mm，轴向长度L=4.53mm，环壁厚度t=0.25mm，见图1。边界条件及载荷见图2。其控制变量参数为环外臂凹段圆弧角度。除此之外的其它结构参数如：环外臂圆弧半径及水平投影长度、弯道半径等均为定值。不同变量参数下的截面几何形状及结构尺寸参数如下图3-4所示（部分）。

2.2 单元类型选择及网格划分

本封严环模型采用PLANE82平面轴对称二次单元。此单元有两个自由度，每个节点有8个节点，分别为x 和y 方向的平移，既可用作平面单元，也可以用作轴对称单元。此外，Plane82单元还具有塑性、蠕变、辐射膨胀、应力刚度、大变形以及大应变的能力。由于采用了非对称接触，故只需对封严环模型进行网格划分。

2.3 边界条件及载荷

在本文中，封严环两端分别固连两刚性平板单元，对其中的上板施加0.4mm的轴向负位移，另一块下板固定。加载完成后模型如图5及6所示。

2.4 应力状况求解

分别对不同变量参数下的有限元模型求解，图7～8分别为变量参数取59.5°及90°时的最大等效应力分布情况，各参数应力详见图9～10。

2.5 金属封严环应力状况分析

考虑到W形环的最大等效应力不可能无限制地增大，取安全系数为1.5，故其最大等效应力不能超过1030/1.5=686.7Mpa。在所有变量参数中， 30.21°～59.5°之间的模型符合强度要求。金属封严环的其他控制参数也可通过以上方法获得[8]-[10]。

3 MOGA优化过程

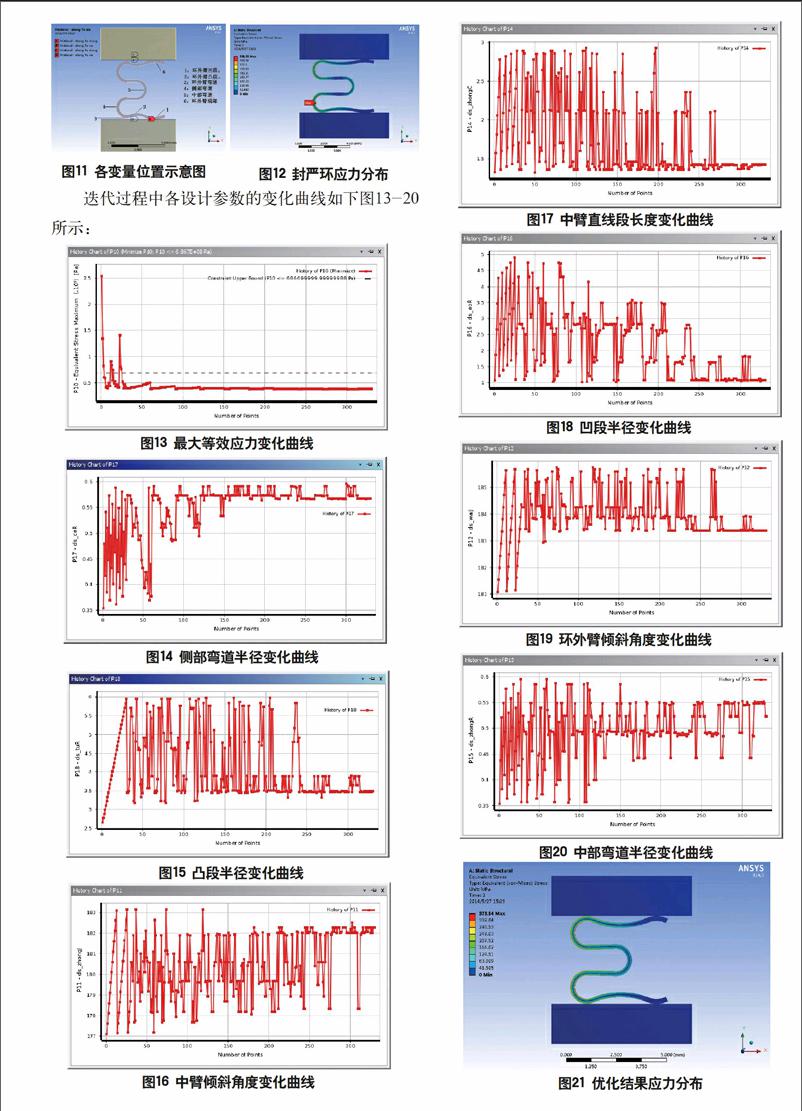
通过以上类似的实验分析得到的各参数合理范围为：环外臂倾斜角度θwai=1°～6°、环中臂倾斜角度θzhong=-3.5°～3°、环外臂凹段半径Rao=1～5mm、环外臂凸段半径Rtu=2.6～6mm、侧部弯道半径Rce=0.35～0.6mm、中部弯道半径Rzhong=0.35～0.6mm及中臂直线段长度Lzhong=1.3～3mm为优化设计变量；将最大等效应力δmax作为优化目标，且δmax<686.7Mpa。其余结构参数及工况参数皆为定值。封严环模型两端分别固连两刚性平板单元，对顶块刚性平板施加0.3mm的轴向负位移，底块刚性平板固定，详见图11。设定初始样本容量为30，每次迭代产生的样本数为30，最大迭代次数为13次。封严环应力分布见图12。

4 优化结果分析

优化在产生318个样本之后收敛，优化结果为：环外臂倾斜角度θwai=3.39°，环中臂倾斜角度θzhong=-2.18°，环外臂凹段半径Rao=1.06mm，环外臂凸段半径Rtu=3.46mm，侧部弯道半径Rce=0.596mm，中部弯道半径Rzhong=0.55mm，中臂直线段长度Lzhong=1.41mm；此时最大等效应力δmax=373.54Mpa。（详见图21）

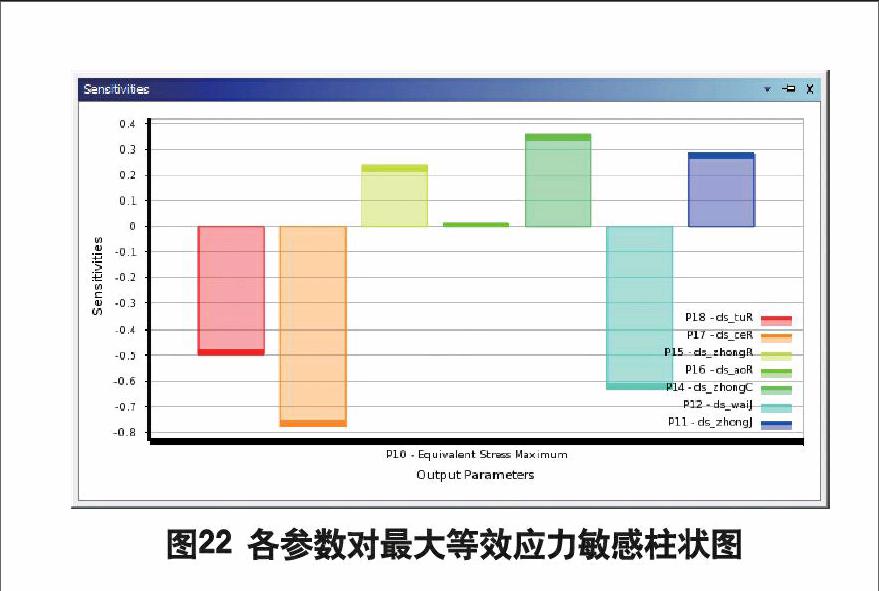
由敏感柱状图（见图22）可以看出：θzhong、Rao、Rzhong及Lzhong对δmax的影响效果相似，其中除Rao外，其余三个参数之间敏感度的差异不大，敏感度的大小关系为Lzhong>θzhong>Rzhong>Rao；相反，Rce、θwai及Rtu对δmax的影响效果相似，并且差异不大，敏感度的大小关系为Rce>θwai>Rtu。

5 结论

利用ANSYS有限元分析软件Workbench Direct Optimization模块的MOGA优化算法（多目标遗传算法）对封严环结构参数进行优化，能够大幅缩短设计周期，并且所设计优化的封严环尺寸合理，同时具有较好的力学性能。本文的不足之处在于没有考虑到温度对封严环力学性能的影响，在以后的设计中会逐渐完善该优化方法。

【本论文受某合金封严环研制（军品配套项目JPPT-125-2-205）资助。】